[省选前集训2021] 模拟赛5
总结
尽力了,感觉确实有很多知识盲点。
\(\tt T3\) 乱贪心可以过掉但是我因为绑点没敢打,下次不管什么我都要乱贪心,管他能不能得分。
还有题一定要仔细看,怎么第一题题又读错了啊。
rng
题目描述
有一个长度为 \(n\) 的序列 \(a_1,a_2...a_n\),\(a_i\) 为在 \([l_i,r_i]\) 中独立均匀随机生成的实数。
求生成数列的期望逆序对个数模 \(998244353\) 的值。
\(n\leq 10^5,l_i<r_i\)
对于 \(20\%\) 的数据:\(l_i=0\)
解法
套路地考虑 \(i<j\) 的时候 \(a[i]>a[j]\) 的概率求和即可。
因为是取 \([l_i,r_i]\) 中的一个实数所以我不会了,其实这种问题主要转化成面积考虑即可。
首先考虑一下部分分 \(l_i=0\) 吧,其实就是在一个 \(r_i\times r_j\) 的矩阵里面选点,要求选到的点横坐标大于纵坐标即可,如下图:
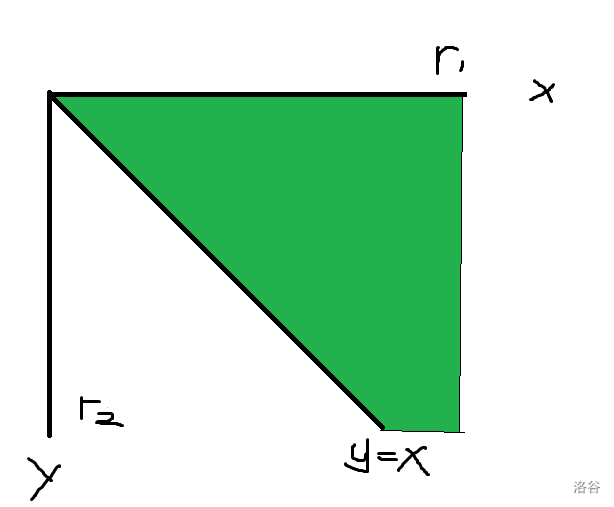
就像上图一样,算面积在总面积里面占的比重就可以了,设 \(f(r_1,r_2)\) 表示对应的面积的两倍,那么分两种情况讨论一下。当 \(r_1\leq r_2\) 时,\(f(r_1,r_2)=r_1^2\),当 \(r_1>r_2\) 时 \(f(r_1,r_2)=2r_1r_2-r_2^2\),概率是 \(\frac{f(r_1,r_2)}{r_1r_2}\)
接下来考虑 \(l_i\not=0\) 的情况,不难发现拿面积减一减就出来了,可以看下图:
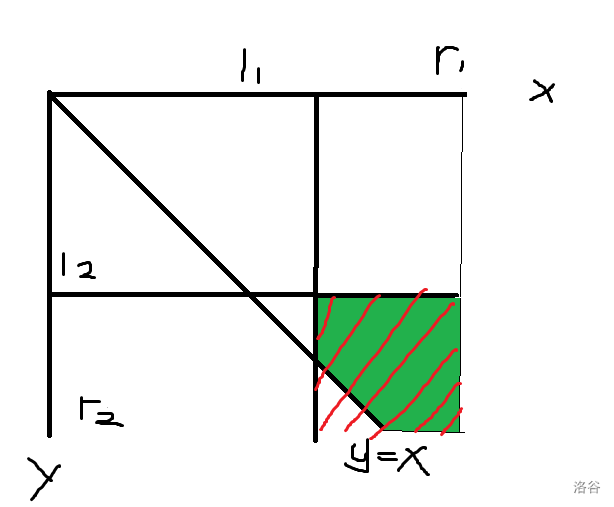
所以核心的柿子是下面这样的:
然后拿六个树状数组维护一下 \(1,x,x^2\) 这三个值就可以快速求 \(f\) 了,写起来其实很方便的,注意中间不要乘爆了,时间复杂度 \(O(n\log n)\),感觉我的代码写的好整齐啊
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 200005;
const int MOD = 998244353;
const int inv2 = (MOD+1)/2;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,a[M],l[M],r[M],b[M][6];
//0-2维护1/x/x^2(l),3-5维护1/x/x^2(r)
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int f,int t)
{
for(int i=x;i<=m;i+=lowbit(i))
b[i][f]=(b[i][f]+t)%MOD;
}
int ask(int x,int f)
{
int res=0;
for(int i=x;i>0;i-=lowbit(i))
res=(res+b[i][f])%MOD;
return res;
}
int fuck(int x,int y)
{
int t1=ask(m,y+1)-ask(x,y+1);
int t=ask(m,y)-ask(x,y),res=0;
res=ask(x,y+2);//r1<=r2
res=(res+2*t1*a[x])%MOD;//r1>r2
res=(res-a[x]*a[x]%MOD*t)%MOD;//r1>r2
return res*inv2%MOD;
}
signed main()
{
freopen("rng.in","r",stdin);
freopen("rng.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
{
l[i]=read();r[i]=read();
a[++m]=l[i];
a[++m]=r[i];
}
sort(a+1,a+m+1);
m=unique(a+1,a+m+1)-a-1;
for(int i=1;i<=n;i++)
{
int inv=qkpow(r[i]-l[i],MOD-2);
l[i]=lower_bound(a+1,a+m+1,l[i])-a;
r[i]=lower_bound(a+1,a+m+1,r[i])-a;
//下面是查询
ans=(ans+fuck(r[i],3)*inv)%MOD;
ans=(ans-fuck(r[i],0)*inv)%MOD;
ans=(ans-fuck(l[i],3)*inv)%MOD;
ans=(ans+fuck(l[i],0)*inv)%MOD;
//下面是修改
add(l[i],0,inv);
add(l[i],1,a[l[i]]*inv%MOD);
add(l[i],2,a[l[i]]*a[l[i]]%MOD*inv%MOD);
add(r[i],3,inv);
add(r[i],4,a[r[i]]*inv%MOD);
add(r[i],5,a[r[i]]*a[r[i]]%MOD*inv%MOD);
}
printf("%lld\n",(ans+MOD)%MOD);
}
lg
题目描述
给定 \(n,m\),求下列柿子:
\(n\leq 10^8,m\leq 200000\)
解法
注意 \(lcm\not=\frac{mul}{\gcd}\) 啊,这个只在两个数的情况下成立,还有就是反演的时候带着 \(lcm\) 走下去是没问题的
看见 \(\tt gcd\) 就直接莫比乌斯反演吧:
先推到这里把,然后你发现问题变成了选一个值域在 \([1,V=\frac{m}{T}]\) 中的序列,求所有情况的 \(lcm\) 的乘积,发现这个完全可以分质数考虑,对于质数 \(p\) 我们枚举 \(lcm\) 中它的次数 \(t\),那么选出来的序列至少要有数包含 \(p^t\) 这个质因子并且所有数 \(p\) 的指数都小于等于 \(t\),这个东西可以简单的容斥并且运用乘法原理知道方案数是这东西:
上面的 \(F(p^i)\) 表示是 \(p^i\) 的倍数但不是 \(p^{i+1}\) 的倍数。
然后就可以算了,现在来说明一下复杂度,\(p,t\) 枚举的复杂度是 \(O(V)\) 的因为枚举出来的 \(p^t\) 两两不同,那么总的时间复杂度就是调和级数求和,由于还要做快速幂,所以总时间复杂度 \(O(m\log m\log n)\)
注意 \(T\) 的指数是 \((\frac{m}{T})^{n}\),因为有那么多种 \(a\) 的排列,还是就是注意指数取模 \(998244353-1\)
#include <cstdio>
const int MOD = 998244353;
const int mod = MOD-1;
const int M = 200005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,cnt,ans=1,p[M],phi[M];
void init(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(!phi[i])
{
phi[i]=i-1;
p[++cnt]=i;
}
for(int j=1;j<=cnt && i*p[j]<=n;j++)
{
if(i%p[j]==0)
{
phi[i*p[j]]=phi[i]*p[j];
break;
}
phi[i*p[j]]=phi[i]*phi[p[j]];
}
}
}
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
int fast(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%mod;
a=a*a%mod;
b>>=1;
}
return r;
}
int lcm(int V)
{
int res=1;
for(int i=1;i<=cnt && p[i]<=V;i++)
{
for(int pt=1;pt<=V;pt*=p[i])
{
int tmp=fast(V-V/(p[i]*pt),n)-fast(V-V/pt,n);
//其实就表示两个后缀相减
tmp=(tmp+mod)%mod;
res=res*qkpow(pt,tmp)%MOD;
}
}
return res;
}
signed main()
{
freopen("lg.in","r",stdin);
freopen("lg.out","w",stdout);
n=read();m=read();
init(m);
for(int i=1;i<=m;i++)
{
int tmp=qkpow(i,fast(m/i,n));
ans=(ans*qkpow(tmp*lcm(m/i)%MOD,phi[i]))%MOD;
}
printf("%lld\n",ans);
}
pm
题目描述
有一个的排列 \(\{a_i\}\),你需要把他变成 \(\{1,2...n\}\)
第一阶段是交换两个相邻的位置,随时可以选择结束第一阶段,第二阶段是任意修改任意一个位置上的值。
最小化总操作步数,输出第一阶段的操作即可。
\(n\leq 2\cdot 10^5\)
解法
定义段表示每个元素都必须参与交换的一个区间,且交换次数至少是 \(len-1\),那么问题变成了把原序列划分成若干个段 \([l,r]\),使得段内元素集合是 \([l,r]\),并且逆序对个数是 \(r-l\)(交换次数)
考虑 \(dp\),设 \(dp[r]\) 表示划分到 \(r\) 的最小步数,但是 \(r\) 可能有多个对应的 \(l\) 满足条件,我们选取哪一个呢?选取最近的那一个即可,这是由于如果选取了更长的段,我们显然可以用这个段将它分开。
那么问题变成了快速找到第一个满足条件的左端点,首先考虑元素集合是 \([l,r]\) 怎么判断,首先里面的元素要小于等于 \(r\),然后满足 \(\sum_{i=l}^r(a_i-i)=0\),所以做出 \(a_i-i\) 的前缀和即可,找到左边第一个相等的位置。
接下来就检查 \([l,r]\) 的逆序对是否是 \(r-l\),因为它的元素集合 \([l,r]\),所以用 \([1,r]\) 的逆序对减去 \([1,l-1]\) 的逆序对,减去 \([1,l-1]\) 中大于 \(r\) 的数 \(\times(r-l+1)\) 即可,可以用可持久化线段树维护,时间复杂度 \(O(n\log n)\)
上面的方法是垃圾,现在来讲正解。
正着扫一遍,如果能换就换,如果你觉得不保险再倒着扫一遍,时间复杂度 \(O(n)\)
但是正着扫一遍就过了
#include <cstdio>
#include <map>
using namespace std;
const int M = 200005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[M],ans[M];
signed main()
{
freopen("pm.in","r",stdin);
freopen("pm.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
if(a[i]==i+1 || a[i+1]==i)
{
ans[++m]=i;
swap(a[i],a[i+1]);
}
printf("%d\n",m);
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号