「解题报告」[NOI2018]冒泡排序 (DP + Catalan 数)
题意
已知排列 \(p\) 冒泡排序的一个交换次数的下界是 \(\frac{1}{2} \sum_{i=1}^{n} |i - p_i |\).
给定一个长度为 \(n\) 排列 \(q\), 求字典序严格大于 \(q\) 且满足冒泡排序交换次数为 \(\frac{1}{2} \sum_{i=1}^{n} |i - p_i |\) 的排列 \(p\) 的个数.
\(n \le 6 \times 10^5\).
思路
基本思路
首先, 冒泡排序交换次数为 \(\frac{1}{2} \sum_{i=1}^{n} |i - p_i |\) 这个条件显然不能直接用, 所以我们考虑把它转化一下.
由题目中对于这个下界的证明可以得到, 当且仅当在排序过程中 \(p\) 中的数只朝一个方向移动 (即数 \(p_i\) 的移动次数是 \(| i - p_i |\)) 时, 排列 \(p\) 能达到这个下界.
为了方便描述 & 理解, 我们设 \(pl_i\) 为数字 \(i\) 在排列 \(p\) 中的位置.
-
若 \(pl_i \le i\), 则 \(pl_i\) 前面不存在大于 \(i\) 的数字 \(j\) (否则会使 \(i\) 往前移动一位);
-
若 \(pl_i \ge i\), 则 \(pl_i\) 后面不存在小于 \(i\) 的数组 \(k\) (否则会时 \(i\) 往后移动一位).
现在条件稍微直观了一点, 但它还是对于单个数的条件, 我们看看能不能把它变成对于排列整体的条件.
我们可以根据上面的条件得到它的逆否命题, 即
- 若 \(pl_i\) 前面存在大于 \(i\) 的数字 \(j\), 即 \(\exist j >i\) 满足 \(pl_j < pl_i\), 则 \(pl_i > i\);
- 若 \(pl_i\) 后面存在小于 \(i\) 的数字 \(k\), 即 \(\exist k < i\) 满足 \(pl_k > pl_i\), 则 \(pl_i < i\).
当上面两个条件同时成立时 \(pl_i \in \empty\).
所以 \(\not \exist k < i < j\) 满足 $ pl_k > pl_i > pl_j$.
用人话来说, 就是排列 \(p\) 中不存在长度 \(\ge 3\) 的下降序列.
所以,可以把排列 \(p\) 分为 $ \le 2$ 个上升序列.
这样, 我们就把原条件变为了排列 \(p\) 能够被分为 $ \le 2$ 个上升序列, 可以用 DP 解决.
先不考虑字典序的限制. 设 \(f[i][j]\) 为已经填上了前 \(i\) 位数, 大于 \(\max_{k=1}^{i} p_k\) 且未被填上的数有 \(j\) 个.
设我们已经求出了 \(f[i-1][j]\), 考虑如何转移到 \(f[i][j']\).
有两种情况
- 在第 \(i\) 位填上一个大于 \(max_{k=1}^{i-1} p_k\) 的数, 转移到 \(f[i][j-1 \sim 0]\);
- 在第 \(i\) 位填上一个小于 \(max_{k=1}^{i-1} p_k\) 的数. 由于排列中最多只能有 \(2\) 个上升序列, 所以我们只能填上目前未被选上的数中的最小值, 否则就会产生 \(3\) 个上升序列. 转移到 \(f[i][j]\).
注意 : 当 \(j=n-(i-1)\) 时, 未被选上的数都大于 \(max_{k=1}^{i-1} p_k\), 所以不能进行第二种转移.
边界条件 : \(f[0][n]=1\). 最终答案 : \(ans = f[n][0]\).
再来考虑字典序的限制.
考虑模仿数位 DP. 对排列 \(q\) 求出 \(s[i]\), 表示 \(i\) 后面比 \(\max_{k=1}^{i} q_k\) 更大的数的个数. 这可以用树状数组求, 也可以模仿上述 DP 的实际过程线性求得.
当 DP 进行到 \(i\) 时, 我们对 \(f[i][s[i]-1 \sim 0]++\), 表示前 \(i-1\) 位与 \(q\) 相同, 第 \(i\) 位大于 \(q\) 的情况. 剩余部分按照过程转移就行了.
这个 DP 的时间复杂度是 \(O(n^3)\) 的, 加上前缀和优化可以达到 \(O(n^2)\), 获得 \(80pts\).
优化
数形结合.
我们再来看一下上述 DP 的转移方程
\(i \in [0,n],\ j \in [0,n-i]\).
我们把 \(f[i][j]\) 看作是平面直角坐标系上的点 \((i,j)\), 可以画出来一张这样的图.

当不考虑字典序限制时, 答案为从点 \((0,n)\) 到 \((n,0)\) 且不穿过直线 \(y=-x+n\) 的最短路径方案数, 也就是 \(Catalan\) 数.
考虑字典序限制时, 相当于固定了若干个起点 \((i, s[i-1] \sim 0)\), 然后求这些起点到 \((n,0)\) 的方案数之和.
求点 \((i,j)\) 到 \((n,0)\) 的不穿过直线 \(y=-x+n\) 的方案数, 我们可以模仿 \(Catalan\) 数的求法.
作点 \((i,j)\) 关于直线 \(y = -x + n-1\) 的对称点, 易得其坐标为 \((n-j+1,n-i+1)\).
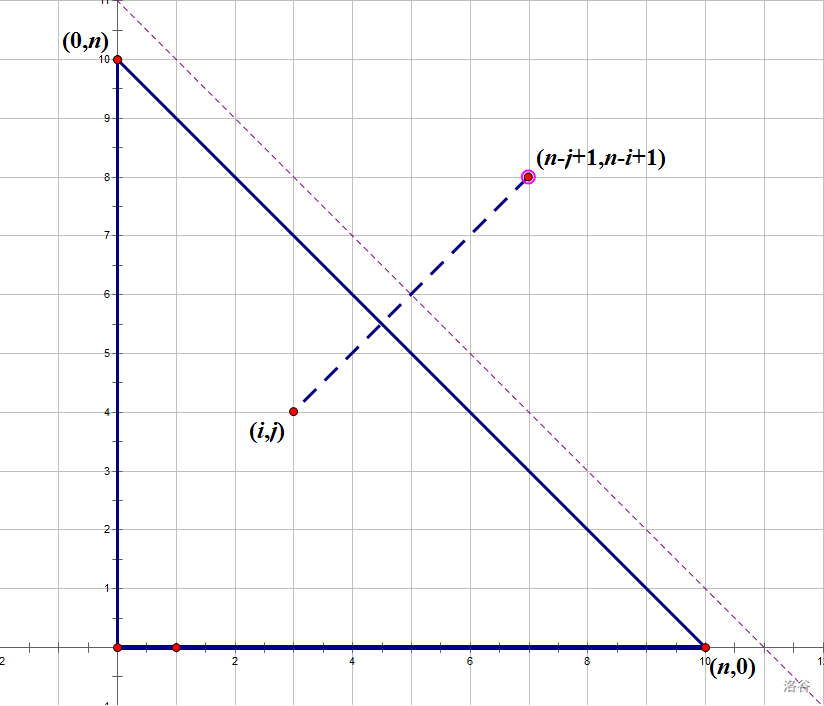
由图可知, 点 \((n-j+1,n-i+1)\) 到 \((n,0)\) 的每条最短路径都会穿过直线 \(y = -x + n-1\), 并且每条路径都会对应着一条从 \((i,j)\) 到 \((n,0)\) 的穿过直线 \(y = -x + n\) 的最短路径.
所以, \((i,j)\) 到 \((n,0)\) 的不穿过直线 $ y = -x + n$ 的最短路径数量为
设其为 \(F(i,j)\), 那么我们的最终答案就是
这样做还是 \(O(n^2)\) 的. 但我们注意到, 点 \((i,s[i]-1 \sim 0)\) 到 \((n,0)\) 的路径数量之和其实就相当于 \((i-1,s[i]-1)\) 到 \((n,0)\) 的路径数量. 所以答案式可以改写为
可以 \(O(n)\) 完成.
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int _=2e6+7;
const int mod=998244353;
int n,q[_],s[_],fac[_],invf[_];
bool b[_];
int gi(){
int x=0; char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x;
}
int Pw(int a,int p){
int res=1;
while(p){
if(p&1) res=(ll)res*a%mod;
a=(ll)a*a%mod; p>>=1;
}
return res;
}
void Pre(){
int n=2e6;
fac[0]=1; for(int i=1;i<=n;i++) fac[i]=(ll)fac[i-1]*i%mod;
invf[n]=Pw(fac[n],mod-2); for(int i=n-1;i>=0;i--) invf[i]=(ll)invf[i+1]*(i+1)%mod;
}
void Init(){
memset(s,-1,sizeof(s));
memset(b,0,sizeof(b));
n=gi();
for(int i=1;i<=n;i++)
q[i]=gi();
int j=n,minx=1;
for(int i=1;i<=n;i++){
int x=n-q[i];
if(x<j) s[i]=x-1,j=x;
else if(q[i]==minx) s[i]=j-1;
else{ s[i]=j-1; break; }
b[q[i]]=1;
while(b[minx]) minx++;
}
}
int C(int n,int m){
if(n<m) return 0;
return (ll)fac[n]*invf[m]%mod*invf[n-m]%mod;
}
int f(int i,int j){ return (C(n-i+j,j)-C(n-i+j,n-i+1)+mod)%mod; }
void pls(int &x,int y){ x=(ll)(x+y)%mod; }
void Run(){
int ans=0;
for(int i=1;i<=n;i++)
if(s[i]!=-1)
pls(ans,f(i-1,s[i]));
printf("%d\n",ans);
}
int main(){
#ifndef ONLINE_JUDGE
freopen("inverse.in","r",stdin);
freopen("inverse.out","w",stdout);
#endif
Pre();
int T=gi();
while(T--){
Init();
Run();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号