【题解·2025 ICPC Nanchang Invitational Contest】L. Regnaissance
简要题意
给定一棵 \(n\) 个点的无根树,请回答下面 \(q\) 次询问:当以点 \(rt_i\) 为根时,编号在 \([l_i,r_i]\) 中的点的 \(\text{LCA}\) 是谁?
数据范围:\(1\leqslant n,q\leqslant3\times10^5\)。
区间 \(\text{LCA}\)
问题:给定一棵 \(n\) 个点的以点 \(rt\) 为根的树,请回答下面 \(q\) 次询问:编号在 \([l_i,r_i]\) 中的点的 \(\text{LCA}\) 是谁?
以点 \(rt\) 为根预处理 \(\text{dfs}\) 序,“编号在 \([l_i,r_i]\) 中的点的 \(\text{LCA}\)”是“在它们中 \(\text{dfs}\) 序最小的和最大的两个点的 \(\text{LCA}\)”。
该结论较常见,可以自行分类讨论证明。
换根 \(\text{LCA}\)
问题:给定一棵 \(n\) 个点的无根树,请回答下面 \(q\) 次询问:当以点 \(rt_i\) 为根时,点 \(u_i,v_i\) 的 \(\text{LCA}\) 是谁?
选定一个点为根(下文选定点 \(1\) 为根)预处理 \(\text{LCA}\)。“当以点 \(rt_i\) 为根时,点 \(u_i,v_i\) 的 \(\text{LCA}\)”是“当以点 \(1\) 为根时,在点 \(rt_i,u_i\) 的 \(\text{LCA}\)、点 \(rt_i,v_i\) 的 \(\text{LCA}\) 和点 \(u_i,v_i\) 的 \(\text{LCA}\) 中深度最大的点”。
该结论较常见,可以自行分类讨论证明。
换根区间 \(\text{LCA}\)
即为本题。
选定一个点为根(下文选定点 \(1\) 为根)预处理 \(\text{dfs}\) 序和 \(\text{LCA}\)。
在以 \(\text{dfs}\) 序为下标的点的编号的序列上,在以 \(rt_i\) 为根的子树对应的区间和它的两个补区间(即在该序列上,下标为 \([1,\text{dfs}_{rt_i}-1],[\text{dfs}_{rt_i},\text{dfs}_{rt_i}+\text{size}_{rt_i}-1],[\text{dfs}_{rt_i}+\text{size}_{rt_i},n]\) 的三个区间,其中 \(\text{size}_{rt_i}\) 表示以 \(rt_i\) 为根的子树的点数)中各自找到最靠近区间左端点和右端点的编号在 \([l_i,r_i]\) 中的点,下文把这六个点称为关键点。“当以点 \(rt_i\) 为根时,编号在 \([l_i,r_i]\) 中的点的 \(\text{LCA}\)”是“当以点 \(rt_i\) 为根时,这六个关键点的 \(\text{LCA}\)”。
利用区间 \(\text{LCA}\) 的结论,简要证明:
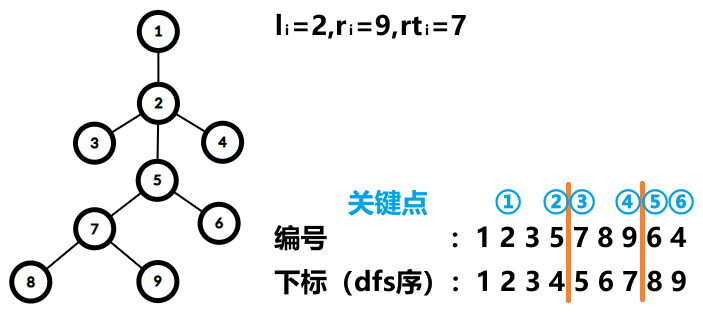
关键点 ① 的存在性和关键点 ② 的一致,关键点 ③ 的存在性和关键点 ④ 的一致,关键点 ⑤ 的存在性和关键点 ⑥ 的一致。
在下面证明过程中,以点 \(1\) 为根,但是 \(\text{LCA}\) 都指的是以点 \(rt_i\) 为根的 \(\text{LCA}\)。
-
当关键点 ③ 存在时,
-
当关键点 ① 存在或者关键点 ⑤ 存在时,区间的 \(\text{LCA}\) 和关键点的 \(\text{LCA}\) 都为点 \(rt_i\)。
-
当关键点 ① 不存在并且关键点 ⑤ 不存在时,可以构造一个以点 \(rt_i\) 为根的 \(\text{dfs}\) 序,满足在编号在 \([l_i,r_i]\) 中的点中 \(\text{dfs}\) 序最小的点为关键点 ③,最大的点为关键点 ④,区间的 \(\text{LCA}\) 和关键点的 \(\text{LCA}\) 都为关键点 ③ 和关键点 ④ 的 \(\text{LCA}\)。
-
-
当关键点 ③ 不存在时,
我们希望在点 \(1\) 到点 \(rt_i\) 的简单路径上,找到一个最接近点 \(rt_i\) 的点 \(u\),满足在以点 \(u\) 为根的子树中存在编号在 \([l_i,r_i]\) 中的点。以点 \(u\) 为根的子树中的编号在 \([l_i,r_i]\) 中的点即为关键点 ② 或者关键点 ⑤。
-
当在以点 \(u\) 为根的子树外存在编号在 \([l_i,r_i]\) 中的点时,这个点即为关键点 ① 或者关键点 ⑥,区间的 \(\text{LCA}\) 和关键点的 \(\text{LCA}\) 都为点 \(u\)。
-
当在以点 \(u\) 为根的子树外不存在编号在 \([l_i,r_i]\) 中的点时,可以构造一个以点 \(rt_i\) 为根的 \(\text{dfs}\) 序,满足在编号在 \([l_i,r_i]\) 中的点中 \(\text{dfs}\) 序最小的点为关键点 ② 或者关键点 ⑤,最大的点为关键点 ① 或者关键点 ⑥,区间的 \(\text{LCA}\) 和关键点的 \(\text{LCA}\) 都为关键点 ①②⑤⑥ 的 \(\text{LCA}\)。
-
求关键点
这个问题可以抽象为:在一个序列上多次求出满足小于等于 \(idx_i\) 且对应的元素值在 \([l_i,r_i]\) 内的最大下标。
方法有很多种,下面给出一种离线加线段树的方法:建立一棵线段树,线段树上代表 \([l_i,r_i]\) 的点表示在当前已插入的信息中对应的元素值在 \([l_i,r_i]\) 内的最大下标。将询问按 \(idx_i\) 从小到大排序。对于一个询问,将该序列上下标小于等于 \(idx_i\) 的元素插入线段树,然后用线段树查询对应的元素值在 \([l_i,r_i]\) 内的最大下标。
本题代码
时间复杂度:\(O(Q\log N)\)。空间复杂度:\(O(N\log N)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e5+10,M=N*2;
int n,q;
int h[N],e[M],ne[M],idx;
int dfn[N],idf[N],num;
int siz[N],dep[N],fa[N][20];
int key[N][7];
struct Query
{
int i,l,r,id[2];
bool operator < (const Query & that) const
{
return i<that.i;
}
}qu[2][N*3];
struct Segment_tree
{
int l,r;
int mi,ma;
}tr[N*4];
void add(int u,int v)
{
e[++idx]=v,ne[idx]=h[u],h[u]=idx;
return ;
}
void dfs(int u)
{
num++;
dfn[u]=num,idf[num]=u,siz[u]=1;
for(int i=h[u];i!=0;i=ne[i])
{
int v=e[i];
if(v==fa[u][0]) continue;
dep[v]=dep[u]+1;
fa[v][0]=u;
for(int k=1;k<=18;k++) fa[v][k]=fa[fa[v][k-1]][k-1];
dfs(v);
siz[u]+=siz[v];
}
return ;
}
int lca(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
for(int k=18;k>=0;k--)
if(dep[fa[u][k]]>=dep[v])
u=fa[u][k];
if(u==v) return u;
for(int k=18;k>=0;k--)
if(fa[u][k]!=fa[v][k])
u=fa[u][k],v=fa[v][k];
return fa[u][0];
}
int lca_rt(int rt,int u,int v)
{
if(!u || !v) return u|v;
int res=0;
int p=lca(rt,u);
if(dep[p]>dep[res]) res=p;
p=lca(rt,v);
if(dep[p]>dep[res]) res=p;
p=lca(u,v);
if(dep[p]>dep[res]) res=p;
return res;
}
void pushup(int u)
{
tr[u].mi=min(tr[u<<1].mi,tr[u<<1|1].mi);
tr[u].ma=max(tr[u<<1].ma,tr[u<<1|1].ma);
return ;
}
void build(int u,int l,int r)
{
tr[u]={l,r,n+1,0};
if(l==r) return ;
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
return ;
}
void change(int u,int x,int val)
{
if(tr[u].l==tr[u].r)
{
tr[u].mi=tr[u].ma=val;
return ;
}
int mid=(tr[u].l+tr[u].r)>>1;
if(x<=mid) change(u<<1,x,val);
else change(u<<1|1,x,val);
pushup(u);
return ;
}
int query_mi(int u,int l,int r)
{
if(l<=tr[u].l && tr[u].r<=r) return tr[u].mi;
int mid=(tr[u].l+tr[u].r)>>1,mi=n+1;
if(l<=mid) mi=min(mi,query_mi(u<<1,l,r));
if(r>mid) mi=min(mi,query_mi(u<<1|1,l,r));
return mi;
}
int query_ma(int u,int l,int r)
{
if(l<=tr[u].l && tr[u].r<=r) return tr[u].ma;
int mid=(tr[u].l+tr[u].r)>>1,ma=0;
if(l<=mid) ma=max(ma,query_ma(u<<1,l,r));
if(r>mid) ma=max(ma,query_ma(u<<1|1,l,r));
return ma;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
add(u,v),add(v,u);
}
dep[1]=1;
dfs(1);
for(int i=1;i<=q;i++)
{
int l,r,rt;
cin>>l>>r>>rt;
key[i][0]=rt;
qu[1][i*3-2]={1,l,r,{i,1}};
qu[0][i*3-2]={dfn[rt]-1,l,r,{i,2}};
qu[1][i*3-1]={dfn[rt],l,r,{i,3}};
qu[0][i*3-1]={dfn[rt]+siz[rt]-1,l,r,{i,4}};
qu[1][i*3]={dfn[rt]+siz[rt],l,r,{i,5}};
qu[0][i*3]={n,l,r,{i,6}};
}
sort(qu[0]+1,qu[0]+3*q+1);
build(1,1,n);
for(int i=1,j=0;i<=3*q;i++)
{
while(j+1<=qu[0][i].i)
{
j++;
change(1,idf[j],j);
}
key[qu[0][i].id[0]][qu[0][i].id[1]]=idf[query_ma(1,qu[0][i].l,qu[0][i].r)];
}
sort(qu[1]+1,qu[1]+3*q+1);
build(1,1,n);
for(int i=3*q,j=n+1;i>=1;i--)
{
while(j-1>=qu[1][i].i)
{
j--;
change(1,idf[j],j);
}
key[qu[1][i].id[0]][qu[1][i].id[1]]=idf[query_mi(1,qu[1][i].l,qu[1][i].r)];
}
for(int i=1;i<=q;i++)
{
int ans=0;
for(int j=1;j<=6;j++) ans=lca_rt(key[i][0],ans,key[i][j]);
cout<<ans<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号