矩阵快速幂在ACM中的应用

矩阵快速幂在ACM中的应用

16计算机2黄睿博

首发于个人博客http://www.cnblogs.com/BobHuang/

作为一个acmer，矩阵在这个算法竞赛中还是蛮多的，一个优秀的算法可以影响到一个程序的运行速度的快慢，在算法竞赛中常常采用快速幂算法，因为有些递推式及有些问题都可以化为矩阵，所以矩阵快速幂也就有了意义。

首先引入快速幂：

我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，

例如当b=11时 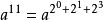 11的二进制是1011

11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1因此，我们将a¹¹转化为算 因为存在这一相等关系，所以将O(n)复杂度的算法降到了O(logn)，代码如下

int poww(int x, int n)
{
    int ans=1;
    while(n)
    {
        if(n&1)ans=ans*x;
        x=x*x;
        n>>=1;
    }
    return ans;
}

这里面用到了一些奇怪的运算，位运算，关于这个详见我的另一篇博客（>>相当于/2，&1相当于判断末位是否为1，比较接近计算机底层，取模还有除法运算常数比较大）

我的矩阵快速幂模板

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
int G;
struct MX
{
    ll v[N][N];
    void O()
    {
        memset(v,0,sizeof v);
    }
    void E()
    {
        memset(v,0,sizeof v);
        for(int i=0; i<G; i++)v[i][i]=1;
    }
    void P()
    {
        for(int i=0; i<G; i++)
            for(int j=0; j<G; j++)printf(j==G-1?"%d\n":"%d ",v[i][j]);
    }
    MX operator+(const MX &b) const
    {
        MX c;
        c.O();
        for(int i=0; i<G; i++)
            for(int j=0; j<G; j++)c.v[i][j]=v[i][j]+b.v[i][j];
        return c;
    }
    MX operator*(const MX &b)const
    {
        MX c;
        c.O();
        for(int k=0; k<G; k++)
            for(int i=0; i<G; i++)
                if(v[i][k])for(int j=0; j<G; j++)c.v[i][j]+=v[i][k]*b.v[k][j];
        return c;
    }
    MX operator^(int p)const
    {
        MX y,x;
        y.E(),memcpy(x.v,v,sizeof(v));
        for(; p; x=x*x,p>>=1)if(p&1)y=y*x;
        return y;
    }
} a,ans;

 

目前c/c++最大支持__int128，也就是最大的有符号整数为2^127-1，数量级大概是1e38，不过常用的还是long long，是长整形，2^63-1。所以常用一个MOD质数的方法，这样得到的答案更加丰富。

引入完毕，接下来进入正题，无非是将以上的乘法转换为矩阵乘法。

我们从最简单的斐波那契数列入手

求菲波那切数列的第n项

n很大，所以MOD1e9+7

斐波的为前两项之和，即发f[0]=1,f[1]=1,f[i] = f[i-1]+f[i-2](i>1)

比较简单的可以直接得到递推式

 

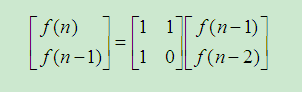
，进一步递推

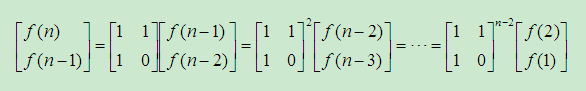
由于矩阵乘法满足结合律，所它也可以用快速幂算法求解。

代码如下

struct Matrix
{
    long long a[2][2];
    Matrix()
    {
        memset(a,0,sizeof(a));
    }
    Matrix operator*(const Matrix  y)
    {
        Matrix  ans;
        for(int i=0; i<=1; i++)
            for(int j=0; j<=1; j++)
                for(int k=0; k<=1; k++)
                    ans.a[i][j]+=a[i][k]*y.a[k][j];
        for(int i=0; i<=1; i++)
            for(int j=0; j<=1; j++)
                ans.a[i][j]%=M;
        return ans;
    }
    void operator=(const Matrix b)
    {
        for(int i=0; i<=1; i++)
            for(int j=0; j<=1; j++)
                a[i][j]=b.a[i][j];
    }
};
long long solve(long long x)
{
    Matrix ans,t;
    ans.a[0][0]=ans.a[1][1]=1;
    t.a[0][0]=t.a[1][0]=t.a[0][1]=1;
    while(x)
    {
        if(x&1)ans=ans*t;
        t=t*t;
        x>>=1;
    }
    return ans.a[0][0];
}

 强行递推式

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1000000009;
unordered_map<ll,ll> M;
ll fic(ll x)
{
    if(M.count(x))return M[x];
    ll a=(x+1)/2,b=x/2+1;
    return M[x]=((fic(a)*fic(b))%mod+(fic(a-1)*fic(b-1)))%mod;
}
int main()
{
    ll n;
    M[0]=0,M[1]=M[2]=1;
    cin>>n;
    cout<<fic(n);
    return 0;
}

 

如果经过推理得到一个递推式呢

如果对矩阵乘法还是不太懂的话，可以先看下这个知乎回答

例子HDU2842

Dumbear likes to play the Chinese Rings (Baguenaudier). It’s a game played with nine rings on a bar. The rules of this game are very simple: At first, the nine rings are all on the bar.

The first ring can be taken off or taken on with one step.

If the first k rings are all off and the (k + 1)th ring is on, then the (k + 2)th ring can be taken off or taken on with one step. (0 ≤ k ≤ 7)

 

Now consider a game with N (N ≤ 1,000,000,000) rings on a bar, Dumbear wants to make all the rings off the bar with least steps. But Dumbear is very dumb, so he wants you to help him.

九连环：如果要拆第n个环，那么第n-1个环就必须在竿上，

前n-2个环都必须已经被拆下，题目是现在是一个n连环，求将n连环全部

拆掉需要的最少的步骤%200907.

如果前k个环被拆掉,第k+1个还被挂着,那么第k+2个就可以拿下或者装上

f[n] = 2 * f[n - 2] + f[n - 1] + 1

 

 

就是f(n)=f[n-1]+2*f[n-2]+1,f[n-1]=1*f[n-1],1=1;

就是可以从前两个状态推到当前状态，这个关系矩阵的系数还是比较好找的

下一个例子

n个六边形排成一行，相邻两个六边形共用一条边，如下图所示：

 

 

 

记这个图形的生成树个数为t(n)（由于每条边都是不同的，不存在同构的问题）。那么t(1)=6，t(2)=35……

给出n，求 mod 1000000007

第i个矩形右边那条边会不会去掉的方案数

dp[i][1]=dp[i-1][0]+dp[i-1][1],

dp[i][0]=4*dp[i-1][1]+5*dp[i-1][0]

i个六边形总个数就是dp[i][0] + dp[i][1];

矩阵就是

 

分析下dp[i+1][2]，这一项已经做了前缀和，所以和之前的总数是不一样的

dp[i+1][2]=dp[i+1][1]+dp[i+1][0]+dp[i][2]=dp[i][0]+dp[i][1]+4dp[i][0]+5dp[i-1][1]+dp[i][2]

=5dp[i][0]+6dp[i][1]+dp[i][2]

所以这个就很好解决了

假设a[i]为当前项的前缀和，很容易发现

a[i] =6*a[i-1] - a[i-2] +5

这个用矩阵怎么填呢

 

可以这样填，还有看到他们最后把a[0][0]-1的，但是相信懂了矩阵乘法的你懂这戏额都是在干嘛

 

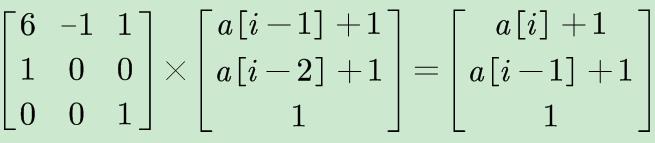
（因为初值的设置不同）

 最后一个例子

一个n位数，它的每位都是奇数，且数字1和3出现偶数次，这样的n位数有多少个。比如说n=1，只有3个，它们分别是5，7和9。让你求下满足这些条件的数的个数MOD9973，对于给定的n都会包含有四种状态，1和3的个数都是奇数；1是奇数，3是偶数；1是偶数，3是奇数；1是偶数，3是偶数。

1是偶数，3是偶数是我想要的状态

在相互转换中其实是可以直接写出系数的

 

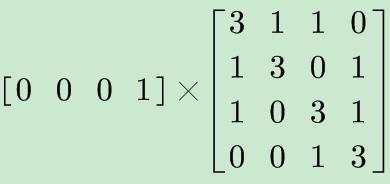
a[0][3]是我们要的状态即为所求

代码如下

#include <stdio.h>
#include <string.h>
const int MD=9973;
struct matrix
{
    int mat[5][5];
};
matrix matmul(matrix a,matrix b,int n)
{
    int i,j,k;
    matrix c;
    memset(c.mat,0,sizeof(c.mat));
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            for(k=0; k<n; k++)
            {
                c.mat[i][j]=(c.mat[i][j]+a.mat[i][k]*b.mat[k][j])%MD;
            }

        }
    }
    return c;
}
matrix matpow(matrix a,int k,int n)
{
    matrix b;
    int i;
    memset(b.mat,0,sizeof(b.mat));
    for(i=0; i<n; i++) b.mat[i][i]=1;
    while(k)
    {
        if(k&1) b=matmul(a,b,n);
        a=matmul(a,a,n);
        k>>=1;
    }
    return b;
}
int main()
{
    int k;
    while(~scanf("%d",&k))
    {
        matrix a,b,ans;
        memset(a.mat,0,sizeof(a.mat));
        memset(b.mat,0,sizeof(b.mat));
        a.mat[0][3]=1;
        for(int i=0; i<4; i++)
        {
            for(int j=0; j<4; j++)
            {
                if(i==j) b.mat[i][j]=3;
                else if(i+j==3) b.mat[i][j]=0;
                else b.mat[i][j]=1;
            }
        }
        ans=matmul(a,matpow(b,k,4),4);
        printf("%d\n",ans.mat[0][3]);
    }
    return 0;
}