高中信息技术(Python)重难点3：最大公约数

本博客原文地址：https://www.cnblogs.com/BobHuang/p/15498007.html，原文体验更佳。

最大公约数在教材必修1 P38、P47以及选修1 P120出现，较为困难，其算法流程、迭代以及递归思想都是教材重难点，属于较为经典的必学算法之一。

一、循环枚举

什么是最大公约数呢？如果整数n除以m，得出结果是没有余数的整数，就称m是n的约数。A和B的最大公约数指A和B公共约数中最大的一个。
教材必修1 P91 整数的因子中介绍我们求一个整数x的因子可以一一列举 \([1,x]\) 范围内的所有整数，如果x能被这个范围内的某个整数整除，那么这个数就是整数x的因子。
那我们解决TZOJ7380: 最大公约数之枚举时，我们也可以一一枚举其因子，最大公约数最小为1，最大公约数最大为数A和B中较小数，即枚举范围为 \([1,\min(A,B)]\) 。
倒着枚举找到公因子即结束循环是比较方便的，参考代码如下所示。
TZOJ7380参考代码1

n=int(input())
m=int(input())
if n<m:
    min_value = n
else:
    min_value = m
for i in range(min_value,0,-1):
    if n%i==0 and m%i==0:
        print(i)
        break

如果枚举初始值为大数并不会影响程序结果，仅会增加循环次数，所以随便选择一个输入的数作为枚举初始值也是正确的。
TZOJ7380参考代码2

n=int(input())
m=int(input())
for i in range(n,0,-1):
    if n%i==0 and m%i==0:
        print(i)
        break

如果从小开始枚举，记录下答案最后输出即可。
TZOJ7380参考代码3

n=int(input())
m=int(input())
for i in range(1,n+1):
    if n%i==0 and m%i==0:
        ans=i
print(ans)

我们还可以分别预处理出A和B的因子，并且因子枚举范围缩小至 \(1\) 至 \(\lfloor{x/2} \rfloor\) ，然后再求出最大公因子。
无论采用以上哪种方法，我们循环枚举求最大公约数的算法复杂度均为\(O(n)\)，即我们需要 n*常数次 循环。

二、因数分解

在数学学习中，我们求最大公约数往往使用质因数分解的方法。
7382: 最大公约数之因数分解 就是这样， 一个整数其质因数分解唯一，比如\(1008=2^4*3^2*7^1\)，\(60=2^2\times3^1\times5^1\)，他们的最大公约数可以把所有因数指数取小而得，即 \(2^2 \times 3^1 \times 5^0\times 7^0=12\) ，最小公倍数可以把所有因数指数取大获得，如下图所示。

我们如何求得质因数分解呢，我们可以找到其质因数，然后将其除尽并统计。这个过程可以和判断素数一样在\(\sqrt x\)次完成，其代码已给出。
质因数分解代码

# 计算质因数分解的字典
def cal_factor_dic(x):
    dic={}
    # 最小因数为2，最大为x**0.5，一一枚举
    for i in range(2,int(x**0.5)+1):
        if x%i==0:
            # 存在质因数i，t存储有几个
            t=0
            # 将其质因数除尽
            while x%i==0:
                t+=1
                x=x//i
            # 将质因数i及其个数存储，质因数作为key，指数作为value
            dic[i]=t
    # 如果没有除尽，存在x这个质因数
    if x>1:
        dic[x]=1
    return dic

那如何将其公因数取小呢，我们可以循环A的因数，如果在B中也存在对指数取小即可，参考代码如下。
TZOJ7382参考代码

def greatest_common_divisor(a,b):
    ans=1
    for i in a:
        if i in b:
            ans=ans*i**min(a[i],b[i])
    return ans

完成了可以尝试下 TZOJ7383: 最小公倍数之因数分解
这个算法的复杂度为\(O(\sqrt n)\)，cal_factor_dic()函数复杂度为\(O(\sqrt n)\)，greatest_common_divisor()函数由于其质因子个数不超过 \(\log n\) 个，所以其复杂度为 \(O(\log n)\)，综合复杂度为\(2*O(\sqrt n)+O(\log n)\)。\(O(\log n)\)与\(O(\sqrt n)\)相比较小可以省略，并忽略常数即为这个算法的复杂度\(O(\sqrt n)\)。

三、更相减损术

7134: 最大公约数之更相减损术 这个算法来源于我们古代数学专著《九章算术》，其文言文描述为“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”
翻译为现代语言如下：
1）任意给定两个正整数，判断它们是否都是偶数。若是，用2约简；若不是，执行 2)；
2）以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数．继续这个操作，直到所得的数相等为止，则这个数（等数）或这个数与约简的数的乘积就是所求的最大公约数。

其算法程序流程图如下所示

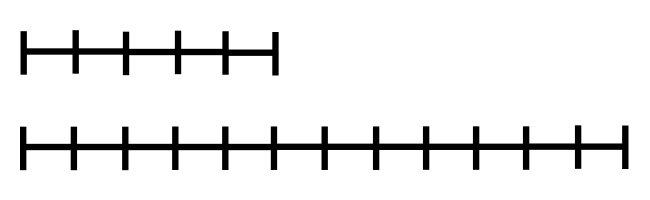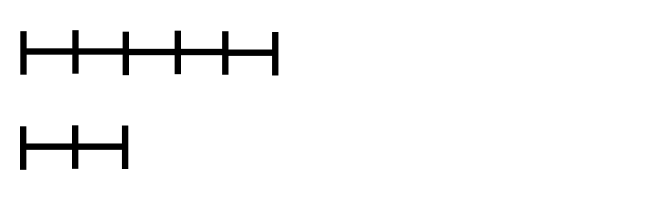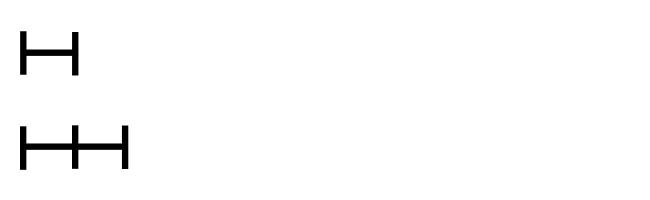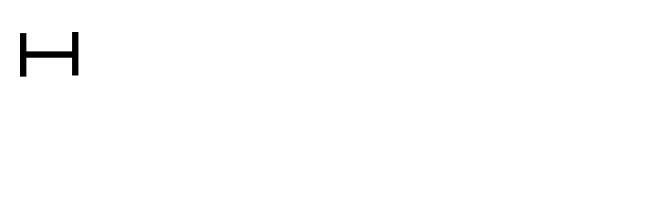
下图可能对你了解这个算法有帮助，看完你可以尝试自己写出代码并提交测试。两条线段长分别可表示252和105，则其中每一小分段长代表最大公约数21。如动画所示，只要辗转地从大数中减去小数，直到其中一段的长度为0，此时剩下的一条线段的长度就是252和105的最大公因数。

7134参考代码1

a=int(input())
b=int(input())
# 存储有多少个2
k=1
# 第一步，求出多少个2
while a%2==0 and b%2==0:
    a=a//2
    b=b//2
    k=2*k
# 第二步，更相减损
while a!=b:
    if a>b:
        a=a-b
    else:
        b=b-a
print(k*a)

第一步为算法优化，直接更相减损也可以，代码如下所示。
7134参考代码2

a=int(input())
b=int(input())
while a!=b:
    if a>b:
        a=a-b
    else:
        b=b-a
print(a)

当然我们也可以使用选修1的递归函数来解决这个问题。
更相减损递归代码

def gcd(a,b):
    if a==b:
        return a
    if a<b:
        return gcd(a,b-a)
    if a>b:
        return gcd(a-b,b)
a=int(input())
b=int(input())
print(gcd(a,b))

Python对递归次数有限制，此代码递归调用次数太多，故无法通过此题。
更相减损代码已比较简洁，但其算法复杂度并没有实质性的变化，如果最大公约数为1，需要运行n次，故其复杂度为\(O(n)\)。

四、辗转相除法

7135: 最大公约数之辗转相除法 辗转相除法是更相减损的一个优化，将其减的过程转换为了取余，算法流程如下：
1)输入两个正整数m和n。
2)若m<n，则交换m和n的值。
3)若m除以n，相除得到的余数r。
4)若r=0，则输出n的值，算法结束；否则，执行步骤5)。
5)令m=n，n=r，返回步骤3)继续执行。

算法流程图如下所示，你可以尝试自己写出代码并提交测试。

我们用死循环模拟其步骤，参考代码如下所示。
7135参考代码1

n=int(input())
m=int(input())
# 死循环
while True:
    # m<n交换
    if m<n:
        m,n=n,m
    # 求出取余值
    r=m%n
    # 为0代表找到了
    if r==0:
        break
    # 执行第5步，缩小范围
    m,n=n,r
print(n)

上述死循环可以使用迭代公式\(gcd(m,n)=gcd(n,m \mod n)\)优化，参考代码如下所示。
7135参考代码2

def gcd(m,n):
    while n!=0:
        temp=n
        n=m%n
        m=temp
    return m

n=int(input())
m=int(input())
print(gcd(n,m))

也可以写为递归形式，参考代码如下所示。
7135参考代码3

def gcd(a,b):
    if b==0:
        return a
    return gcd(b,a%b)

n=int(input())
m=int(input())
print(gcd(n,m))

使用 if表达式 可以将此函数精简函数为1行，参考代码如下所示。
7135参考代码4

def gcd(a,b):
    return a if b==0 else gcd(b,a%b)

n=int(input())
m=int(input())
print(gcd(n,m))

辗转相除法的算法复杂度为\(O(\log n)\)，也是我们常用的求最大公约数方法。这个简单数论在密码学RSA算法也有运用，将其扩展可以求解不定方程、线性同余方程、逆元等，感兴趣的同学欢迎大学选择计算机类专业参加算法竞赛。