山东暑假集训2025 IV

Day 22

为什么会和上一篇有两那个 Day 22？因为写太多了，越来越慢......

题目：P4577。
我们首先考虑一条链的情况。我们会发现，这不就是一个 LIS 问题吗！
好，我们会了链上面的情况，我们考虑放到一棵树上：
如果我们从上往下考虑，发现不太简单。正难则反，我们从下往上，设 \(f_u\) 是 \(u\) 的一个合法最长集合。
首先，我们把下面的所有 \(v\) 的 \(f\) 合并起来（*），
其次，我们把 \(w_u\) 插入到 \(f\) 中：

• 加入 \(w_u\) 不是最小的元素，那么我们把 \(w_u\) 前面的一个元素删掉；
• 否则，我们啥也不干。

*：我们考虑，如果直接随机暴力合并，那么答案就是 \(O(n^2)\)，不够好，我们考虑启发式合并，对于 \(u\) 和 \(v\)，我们每次都把 \(size\) 小的向大的合并，这样复杂度是 \(O(n \log^2n)\) ，也就是 O(能过)。

数位 DP没太听懂，先待补。

Day 23

什么是凸包？那就是凸和包。

题目：没有。
由于笔者在 luogu 上没有找到原题，于是简述一下题意：
现在有 \(n\) 个点，一开始这些点之间没有连边。
接下来有 \(m\) 次询问，每次我们可以选择加一条边或者询问两个点 \(u\)，\(v\) 在多少次操作之后联通即可。

解法：我们考虑类似于启发式合并的并查集合并方式，每次都是把小的向大的合并，不要压缩路径，这样合并出来的复杂度就是 \(O(\log n)\)。
我们再考虑两个点一直向上跳，那么也就是 \(\log n\) 步即可到达 LCA，那么我们考虑直接暴力往上跳，复杂度最大是 \(O(m \log n)\)。

题目：P3556 [POI 2013] MOR-Tales of seafaring。

我们假设 \(s\) 到 \(t\) 的最短路径是 \(5\)，那么要是 \(d = 3\) 那么一定是不可行的；但是，\(d = 7\) 或者 \(d = 9\) 这两种路径都是合法的；
同理，假设 \(s\) 到 \(t\) 的有一条距离是 \(6\)，那么 \(d = 4\) 是不可能的，但是 \(d = 8\)、\(d = 10\) 一定是可行的。
我们发现规律，维护任意两点之间的最短奇数路径、最短偶数路径，考虑 \(d\) 是奇数或者偶数的情况，只要 \(d \ge dis_{s, t, 0/1}\) 即可。

题目：P2865 [USACO06NOV] Roadblocks G。
这道题是一个典的严格次短路的题目，我们考虑记录 \(dis_{i, 0/1}\)，和 dijskra 一样进行更新，同时记得维护是最短还是次短即可。

题目：P4667 [BalticOI 2011] Switch the Lamp On 电路维修 (Day1)。
我们对于每一行和每一列的点进行编号，然后我们考虑对于一个点 \((i, j)\) 向左上、左下、右上、右下的点进行连边，如果相同那么代价是 \(0\)，否则是 \(1\)，最后从起点开始跑一边 dijskra，然后求出到右下角的最短路径即可。

题目：P4568 [JLOI2011] 飞行路线。
典中典，分层图板子题。
我们考虑把分层图复制 \(k\) 次，每一层表示第 \(i\) 条路径免费，每一层之间代价为 \(0\)，层内保留原有边权，跑一边最短路径即可。

wkl：想上厕所的上厕所，想喝水喝水，想去厕所喝水也可以去厕所喝水。

题目：luogu 上应该有，但是我目前没找到。
现在有 \(T\) 个时间段，\(n\) 只奶牛，每只奶牛的值班时间是 \([s_i, e_i]\)，\(T \le 10^6\)，\(n \le 25000\)，求最小需要多少只奶牛。
我们考虑把每个 \(s_i\) 向 \(e_i\) 连边，但是我们发现这个图大概率不连通，所以我们把 \(i\) 向 \(i - 1\) 连一个长度是 \(0\) 的路径，然后再跑最短路径即可。

题目：笔者又双叒叕没有找到 luogu 上的原题，于是简述题面。
给定一个 \(n\) 个点 \(m\) 条无向图，有一些边只能在奇数步走，另外一些只能在偶数步走，剩下的都可以，求最短路径。

我们考虑分层图，分成两层，一层是奇数，另一个是偶数，如果两个都可以的话那么都加入。我们把奇数和偶数之间连一条边，再跑一边最短路即可。

P2371 [国家集训队] 墨墨的等式。
我们考虑同余最短路，我们把 \(a\) 进行排序，按照 \(a_1\) 余数建图。然后对于每一个点 \(a_i\)，都向现在的 \((u + a_i)\) 模 \(a_1\) 意义下连一条边，跑一条最短路径即可。

题目：luogu 上没有。
我们有一个在 \(xOy\) 下的 \(n\) 个点，每个点都有一个坐标 \((x_i, y_i)\)。两个点之间的距离定义为 \(\min (|x_i - x_j|, |y_i - y_j|)\)，求 \(1\) 到 \(n\) 之间的最短距离。

题目：P2888 [USACO07NOV] Cow Hurdles S。
我们魔改一下 Floyd 做法，我们设 \(dis_{i, j}\) 表示 \(i\) 到 \(j\) 之间的距离。我们进行一些转移：

\[dis_{i, j} = \min (dis_{i, j}, \max (dis_{i, k}, dis_{k, j})) \]

即可。

题目：P3275 [SCOI2011] 糖果：
见山东暑假集训2025 II。

题目：P5994 [PA 2014] Kuglarz。

绝世好题，真的是绝世好题。

我们考虑一个区间 \([l, r]\)，我们不妨魔改成另一个区间 \((l, r]\)，这样我们就会把 \(0\) 号点加进来，然后跑一个最小生成树即可。

Day 24

又是图论+数论的一天。

题目：P3350 [ZJOI2016] 旅行者。
我的评价是：逆天。
我们把这个矩形沿中轴线切开，分为左右两边。我们考虑 \((x1, y1)\) 和 \((x2, y2)\) 一定是分列在中轴线的左右两侧。接下来，我们沿着中轴线，对于中轴线上的每一个点进行一次最短路的计算，然后我们计算出这个点到中轴线上每个点的距离，然后进行枚举，找出最短路径即可。
然后我们考虑不跨过中轴线的可能，我们递归左半区间，再递归右半区间，重复上述过程即可。对于询问我们要进行离线处理。
我们记 \(S = n \times m\)，\(m \le n\)，那么复杂度大致是 \(O(S \times \sqrt S \times \log S + m \times q)\)，也即是 \(O(能过)\)。

题目：P3505 [POI 2010] TEL-Teleportation。
我先放一个图：

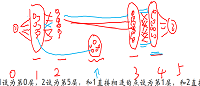
我们通过观察，我们会发现，现在处于 \(0\) 层和 \(0\) 层不可能和中间的散点直接连边，因为这样就会不合法，也就是说，处于中间散点只能和 \(1\) 层和 \(4\) 层的点进行连边，也就是说它终将会划入 \(2\) 层后者 \(3\) 层当中。
我们现在设第 \(i\) 层有 \(x_i\) 个点，那么我们直接暴力枚举中间的散点，设有 \(a\) 个散点划入 \(2\) 层，总共有 \(T\) 个散点，那么我们可以算出总共的边的数量：

\[x_1 + \frac{x_1 \times (x_1 - 1)}{2} + x_1 \times x_2 + \frac{x_2 \times (x_2 - 1)}{2} + x_2 \times x_3 + \frac{x_3 \times (x_3 - 1)}{2} + x_3 \times x_4 + \frac{x_4 \times (x_4 - 1)}{2} + x_4 \]

暴力枚举 \(a\) 计算上式即可。
对了，这个题其实也可以 \(O(1)\) 得出上式的 max，可以使用二次函数相关知识，但是式子过于复杂，我懒得代入。

题目：P3588 [POI 2015] PUS。
不好写，但是比这个好写。
我们先不考虑建边的复杂度，我们直接把这个区间内的点都建好，这样我们再跑一个拓扑或者是 spfa，如果存在一个环，那么就是无解；否则，我们会发现 \(u\) 的答案可以是 \(dis_u + 1\)，其中 \(dis_u\) 是拓扑最长序。
我们考虑对于建图进行优化，根据我们会看到，这其实是在区间内进行建图，所以我们考虑使用线段树进行建图优化即可。

题目：P4092 [HEOI2016/TJOI2016] 树。
这道题有很多种无脑的数据结构暴力大法，由于笔者数据结构学的很烂，所以这里只讲解一个最快的做法。
我们考虑使用离线做法，我们倒着考虑，也就是我们把打标记换成撤标记。我们考虑并查集，每个点如果被打了标记就向自己连一条边，否则向父亲连一条边。
我们进行路径压缩，直接找到找到第一个节点，如果这个点标记被撤销了，我们就把这个节点 \(u\) 连向 \(father\)，复杂度是 \(O(n \alpha (n))\)，比 \(O(n \log n)\) 更优，所以你看数据结构也不是万能的。

题目：CF708C Centroids。
我们考虑重心的定义，也就是说对于任意的 \(v\)，没有任何一个 \(size_v \ge \frac{n}{2}\)。我们考虑对于一个节点 \(u\)，对于最大的儿子里面我们找出最大的一个子树使得子树的大小 \(\le \frac{n}{2}\)，然后把他加到自己 \(u\) 下边作为一个新的子树，看看能否使得那个节点合法。

题目：luogu 上没有。
简述题意：对于一个 \(n\) 个点、\(m\) 条边的无向图，你必须回答下列两个问题中的一个：

• 进行 \(k\) 染色；
• 找出一条长度为 \(k\) 的简单路径。

注意，以上这两个问题都是 NP 问题，也就是不存在复杂度为多项式解法（除了搜索）的问题。

脑筋急转弯。我们考虑把原图转化成一个 DFS 树，没有横插边，只有向父亲的连边。
我们考虑这个 DFS 的深度为 \(d\)，如果 \(d \le k\)，那么我们每层染一个即可；
如果 \(d > k\)，我们就找到了一条长度为 \(k\) 的简单路径。没了。

题目：luogu 上没有。
简述题意：我们现在有一棵 \(n\) 个节点的树。现在给出 \(m\) 组询问，没次给定 \(a, b, c, d\)，要求在 \([a, b]\) 中选择一个 \(u\)，\([c, d]\) 中选择一个 \(v\)，要求我们找出 \(\max dis(u, v)\)。

数学

题目：P4139 上帝与集合的正确用法。
我们记录 \(\varphi(x)\)，其中 \(1 \le x \le 10^7\)，提前预处理出来，我们根据万恶的扩展欧拉定理：

\[a^b \equiv a ^ {b \mod \varphi(p) + \varphi(p)} \pmod p \]

然后根究上面这个式子直接进行递归求解即可。

题目：P1082 [NOIP 2012 提高组] 同余方程。
板子，可以不讲。

题目：P1869 愚蠢的组合数。
我们根据万恶的卢卡斯定理：

\[C_{n}^{m} = C_{n \mod p}^{m \mod p} \times C_{\frac{n}{p}}^{\frac{m}{p}} \]

其实也可以换一种理解方式，也就是把 \(n\) 和 \(m\) 都拆成 \(p\) 进制数，然后把每一位的对应组合数乘起来。

二项式定理：

\[(a + b)^n = \sum_{i = 0}^{n} C_{n}^{i} \times a^{n - i} \times b^i \]

二项式定理扩展版

\[(x_1 + x_2 + ... + x_t) ^ n = \sum_{n_1 + n_2 ... + n_t = n}^{} C_{n_1 \times n_2 \times ... \times n_t}^{n} \times x_1^{n_1} \times x_2^{n_2} \times ... \times x_t^{n_t} \]

一开始，我觉得这可以大大简化我背一些高难度的式子，但是我看到了之后放弃了......

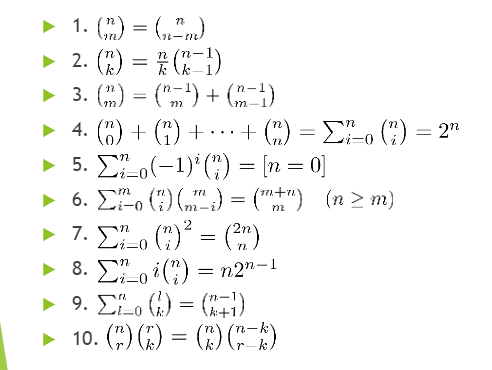
上面是一些其他的重要公式。

题目：P1350 车的放置。
我们考虑如果是 \(k \times k\) 的正方形中放入 \(k\) 辆车的方案数。很明显，答案是 \(k!\)。
我们考虑 \(a \times a\) 的正方形中放入 \(k\) 辆车的方案数。很明显，答案是 \(C_{a}^{k} \times C_{a}^{k} \times k!\)。
我们再考虑一下在 \(a \times b\) 中放入 \(k\) 辆车的方案数。很明显，答案是 \(C_{a}^{k} \times C_{b}^{k} \times k!\)。
我们再考虑如原题的情况，很明显，我们考虑 \(t\) 辆车放在 \(c \times d\) 的矩阵中，那么答案就是 \(C_{d}^{t} \times C_{c}^{t} \times t!\)。
再考虑剩下的，也就是相当于把 \(k - t\) 辆车放在 \(a \times (b + d - t)\) 的矩阵中，计算答案即可。

错排

我们设 \(f_n\) 表示 \(n\) 个错排的方案数。
那么递推公式就是 \(f_n = (n - 1) \times (f_{n - 1} + f_{n - 2})\)。

题目：P4071 [SDOI2016] 排列计数。
典。答案是 \(C_{n}^{m} \times f_{n - m}\)。

线性基

题目：P4570 [BJWC2011] 元素。
我们考虑贪心，按照权值进行排序。
我们又考虑线性基，我们对于每一个位置进行枚举，考虑这一位异或上之后是不是 \(0\)，如果不是，那么我们就贪心地把这个数插进来，否则就不管它。可以证明，这样一定是最优的。

分数规划

题目：P4377 [USACO18OPEN] Talent Show G。
典。
我们考虑 01 分数规划，二分一个 \(a\)，表示 \(a\) 是否可以是答案。
那么：

\[\frac{\sum t_i}{\sum w_i} \ge a \]

\[\sum t_i \ge a \times \sum w_i \]

\[\sum t_i - a \times w_i \ge 0 \]

接下来，我们把一头奶牛的新的价值定义为 \(t_i - a \times w_i\)，重量还是 \(w_i\)，再进行 01 背包即可。
拼好题。

wkl：今天的课程上到这里了，明天就是愉快的瞎扯蛋环节。