山东暑假集训2025 I

Day 1 ~ Day 3

Day 1

搜索

xby：搜索就是弱智，大家都会，那就来点不一样的。

折半搜索，顾名思义，就是先搜索前 \(\frac{n}{2}\) ，在搜索后 \(\frac{n}{2}\) 个，再把他们进行整合得到答案。
来看到题目：

P3067 [USACO12OPEN] Balanced Cow Subsets G

题目描述

我们定义一个奶牛集合 \(S\) 是平衡的，当且仅当满足以下两个条件：

• \(S\) 非空。
• \(S\) 可以被划分成两个集合 \(A,B\)，满足 \(A\) 里的奶牛产奶量之和等于 \(B\) 里的奶牛产奶量之和。划分的含义是，\(A\cup B=S\) 且 \(A\cap B=\varnothing\)。

现在给定大小为 \(n\) 的奶牛集合 \(S\)，询问它有多少个子集是平衡的。请注意，奶牛之间是互不相同的，但是它们的产奶量可能出现相同。

输入格式

第一行一个整数 \(n\)，表示奶牛的数目。

第 \(2\) 至 \(n+1\) 行，每行一个数 \(a_i\)，表示每头奶牛的产奶量。

输出格式

输出一个数表示方案总数。

样例解释

共存在三种方案。集合 \(\{1,2,3\}\) 可以划分为 \(\{1,2\}\) 与 \(\{3\}\)；集合 \(\{1,3,4\}\) 可以划分为 \(\{1,3\}\) 与 \(\{4\}\)；集合 \(\{1,2,3,4\}\) 可以划分为 \(\{1,4\}\) 与 \(\{2,3\}\)，共 \(3\) 种子集。

输入输出样例 #1

输入 #1

4 
1 
2 
3 
4

输出 #1

3

说明/提示

对于全部数据，保证 \(1\le n\le 20\)，\(1\le a_i\le 10^8\)。

好的，我们先思考一下普通的搜索：
每个东西都会用三个状态：

• 被选择到 \(A\) 集合中；
• 被选择到 \(B\) 集合中；
• 没有被选择。

解法

这样的话复杂度就是 \(O(3^n)\)，非常快，考虑优化：
我们不妨先搜索前 \(\frac{n}{2}\) 个数，然后可以得到两个集合：\(A_1\) 和 \(B_1\)，再搜索后半程，可以得到两个集合 \(A_2\) 和 \(B_2\)。
设 \(a\) 表示 \(A_1\) 的得分，\(b\) 表示 \(B_1\) 的得分，\(c\) 表示 \(A_2\) 的得分，\(d\) 表示 \(B_2\) 的得分。
根据题意，可得：
\(a + c = b + d\)，
移项可得 \(a - b = d - c\)。
所以，我们对前 \(\frac{n}{2}\) 个记录 \(a - b\)，后 \(\frac{n}{2}\) 记录 \(d - c\)，在通过 map 映射即可。恭喜你，成功A了一道水蓝。

再来一道？

CF2002G Lattice Optimizing

题目描述

考虑一个具有
\(n\) 行和
\(n\) 列的网格图。

对于所有 \(x < n\) 的位置有一个权值 \(d_{x,y}\)

对于所有 \(y < n\) 的位置有一个权值
\(r_{x,y}\)

从 \((1,1)\) 开始走，每次往下或往右走，最终到 \((n,n)\)。

初始有一个空集合 \(S\)。若从 \((x,y)\) 走到 \((x+1,y)\)，将 \(d_{x,y}\) 加入 \(S\)；走到 \((x,y+1)\) 就加入 \(r_{x,y}\)。

需要最大化走到终点时的 \(mex(S)\)

其中，\(mex(x)\) 定义为 \(x\) 中最小未出现的 非负整数。

输入格式

第一行一个数 \(T\)，表示测试组数。

每组测试第一行一个整数 \(n\)，接下来 \(n-1\) 行每行 \(n\) 个数表示 \(d\)。

接下来 \(n\) 行每行 \(n-1\) 个数表示 \(r\)。

保证 \(n\) 不超过 \(20\)，且所有 \(n^3\) 的和不超过 \(8000\)，且 \(d_{i,j}\) 和 \(r_{i,j}\) 都不超过 \(2n-2\)。

输出格式

输出 \(T\) 行表示每组测试数据的答案。

输入输出样例 #1

输入 #1

2
3
1 0 2
0 1 3
2 1
0 3
3 0
3
1 2 0
0 1 2
2 0
1 2
0 1

输出 #1

3
2

输入输出样例 #2

输入 #2

1
10
16 7 3 15 9 17 1 15 9 0
4 3 1 12 13 10 10 14 6 12
3 1 3 9 5 16 0 12 7 12
11 4 8 7 13 7 15 13 9 2
2 3 9 9 4 12 17 7 10 15
10 6 15 17 13 6 15 9 4 9
13 3 3 14 1 2 10 10 12 16
8 2 9 13 18 7 1 6 2 6
15 12 2 6 0 0 13 3 7 17
7 3 17 17 10 15 12 14 15
4 3 3 17 3 13 11 16 6
16 17 7 7 12 5 2 4 10
18 9 9 3 5 9 1 16 7
1 0 4 2 10 10 12 2 1
4 14 15 16 15 5 8 4 18
7 18 10 11 2 0 14 8 18
2 17 6 0 9 6 13 5 11
5 15 7 11 6 3 17 14 5
1 3 16 16 13 1 0 13 11

输出 #2

14

解法

我们可以发现，从 \((1,1)\) 走到 \((n,n)\) 一共会走 \(2n - 2\) 步。我们考虑从 \((1,1)\) 走 \(B\) 步，再从 \((n,n)\) 走 \(2n - 2 - B\) 步。我们发现，这两个点一定是在一条直线上的。
我们再来考虑如何判断是不是满足前 \(t - 1\) 位都是 \(1\)，我们考虑 \(2 ^ t - 1 - t_j\) 是否在 \(S_i\) 的子集中即可。我们把每一个 \(S_i\) 找到它的所有子集，加入一个 map 中，再来查找即可。

二分

xby:没啥好讲的
xby:来给大家震撼一下OI中的思维题。

AT_agc006_d [AGC006D] Median Pyramid Hard

题目描述

$ N $ 段のピラミッドがあります。 段は上から順に $ 1 $, $ 2 $, $ ... $, $ N $ と番号が振られています。 各 $ 1\ <\ =i\ <\ =N $ について、$ i $ 段目には $ 2i-1 $ 個のブロックが横一列に並んでいます。 また、各段の中央のブロックに注目すると、これらは縦一列に並んでいます。

$ N=4 $ 段のピラミッド

すぬけ君は $ N $ 段目のブロックに ($ 1 $, $ 2 $, $ ... $, $ 2N-1 $) を並べ替えたもの（順列）を書き込みました。 さらに、次のルールに従い、残りすべてのブロックに整数を書き込みました。

• あるブロックに書き込まれる整数は、そのブロックの左下、真下、右下のブロックに書き込まれた整数の中央値である。

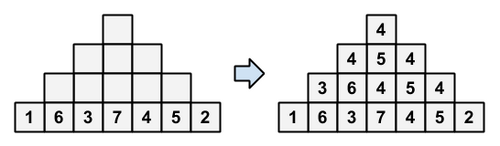ブロックに整数を書き込む例

その後、すぬけ君はすべてのブロックに書き込まれた整数を消してしまいました。 すぬけ君は、$ N $ 段目のブロックに書き込まれた順列が ($ a_1 $, $ a_2 $, $ ... $, $ a_{2N-1} $) であったことだけを覚えています。

$ 1 $ 段目のブロックに書き込まれた整数を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ a_1 $ $ a_2 $ $ ... $ $ a_{2N-1} $

输出格式

$ 1 $ 段目のブロックに書き込まれた整数を出力せよ。

输入输出样例 #1

输入 #1

4
1 6 3 7 4 5 2

输出 #1

4

输入输出样例 #2

输入 #2

2
1 2 3

输出 #2

2

说明/提示

制約

• $ 2\ <\ =N\ <\ =10^5 $
• ($ a_1 $, $ a_2 $, $ ... $, $ a_{2N-1} \() は (\) 1 $, $ 2 $, $ ... $, $ 2N-1 $) の順列である。

Sample Explanation 1

問題文中の図の例です。

解法

我们考虑二分最高层 \(x\)，把所有的大于等于 \(x\) 的数设为 \(1\)，把所有小于 \(x\) 的数字设为 \(0\)。
那么我们就得到了一个 01 序列。怎么考虑它的最高层是 \(0\) 还是 \(1\) 呢？
我们观察一下，并且口胡了一个强大的结论：
如果越靠近中间的且相邻的两个数是一样的，那么这就是最高层的数。
为什么呢？
感性理解一下，越靠近中间的数肯定对于上面的贡献越大，所以这就是对的。

再来一道？

P3199 [HNOI2009] 最小圈

题目描述

考虑带权有向图 \(G=(V,E)\) 以及 \(w:E\rightarrow \R\)，每条边 \(e=(i,j)\)（\(i\neq j\)，\(i, j\in V\)）的权值定义为 \(w_{i,j}\)。设 \(n=|V|\)。

\(c=(c_1,c_2,\cdots,c_k)\)（\(c_i\in V\)）是 \(G\) 中的一个圈当且仅当 \((c_i,c_{i+1})\)（\(1\le i<k\)）和 \((c_k,c_1)\) 都在 \(E\) 中。称 \(k\) 为圈 \(c\) 的长度，同时记 \(c_{k+1}=c_1\)，并定义圈 \(c=(c_1,c_2,\cdots,c_k)\) 的平均值为

\[\mu(c)= \frac 1 k \sum\limits_{i=1}^{k} w_{c_i,c_{i+1}} \]

即 \(c\) 上所有边的权值的平均值。设 \(\mu'(G)=\min_c\mu(c)\) 为 \(G\) 中所有圈 \(c\) 的平均值的最小值。

给定图 \(G=(V,E)\) 以及 \(w:E\rightarrow \R\)，求出 \(G\) 中所有圈 \(c\) 的平均值的最小值 \(\mu'(G)\)。

输入格式

第一行两个正整数，分别为 \(n\) 和 \(m\)，并用一个空格隔开。其中 \(n=|V|\)，\(m=|E|\) 分别表示图中有 \(n\) 个点 和 \(m\) 条边。

接下来 \(m\) 行，每行三个数 \(i,j,w_{i,j}\)，表示有一条边 \((i,j)\) 且该边的权值为 \(w_{i,j}\)，注意边权可以是实数。输入数据保证图 \(G=(V,E)\) 连通，存在圈且有一个点能到达其他所有点。

输出格式

一个实数 \(\mu'(G)\)，要求精确到小数点后 \(8\) 位。

输入输出样例 #1

输入 #1

4 5
1 2 5
2 3 5
3 1 5
2 4 3
4 1 3

输出 #1

3.66666667

输入输出样例 #2

输入 #2

2 2
1 2 -2.9
2 1 -3.1

输出 #2

-3.00000000

说明/提示

对于 \(100\%\) 的数据，\(2\leq n\le 3000\)，\(1\leq m\le 10000\)，\(|w_{i,j}| \le 10^7\)，\(1\leq i, j\leq n\) 且 \(i\neq j\)。

---

提示：本题存在 \(O(nm)\) 的做法，但是 \(O(nm\log n)\) 的做法也可以通过。

解法：

我们考虑二分平均数 \(x\)，如果 $ x \le \frac 1 k \sum\limits_{i=1}^{k} w_{c_i,c_{i+1}} $，那么我们可以得到结论 \(\sum\limits_{i = 1}^{k}x\times k - w_{c_i, c_{i+1}} \le 0\)。
我们把每条边都剪掉 \(x\)，再判断负环即可。

贪心

xby:贪心就是一种直觉！

来看一道试题：CF1637F Towers。
解法：我们通过直觉观察可以发现，这个东西一定会种在叶子节点上。我们不妨找出 \(h_i\) 最大的点作为根节点，然后向随机两个儿子下放。其他的叶子节点在其子树内的最大值只要大于 \(h_i\)，那么一定符合答案。
再来一道？
P1484 种树。
这道题是一道反悔贪心的题目。我们通过直觉发现，如果我们选择编号为 \(i\) 的树，那么 \(i - 1\) 和 \(i + 1\) 都是不可以选的。
所以，我们设置一个反悔机制，当我们拿出第 \(i\) 个树后，我们把 \(a_{i - 1} + a_{i + 1} - a_i\) 这个数字替换成 \(i\)，再进行贪心的选择即可。
当我们再一次选择它时，我们会得到 \(a_i + a_{i - 1} + a_{i + 1} - a_i = a_{i - 1} + a_{i + 1}\) 的恒等式，也就是相当于选择了 \(i - 1\) 和 \(i + 1\) 这两个树。
再来一道？
好，看看这个AT_agc023_f [AGC023F] 01 on Tree，别一看紫题就想放弃，我们来思考一下：
首先，我们贪心的想，一定是要把 \(0\) 放在前面，\(1\) 放在后面。如果一个节点 \(u\) 的父亲节点为 \(father\)，那么删除了 \(father\) 后立即删除 \(u\) 对于答案是没有任何影响的。所以，我们把 \(p_u = 0\) 的所有的 \(u\) 和父亲节点绑定再一起就可以了。
接下来，这棵树就变成了若干个点组成的点集 \(A\) 的一棵树。假设点集 \(A\) 中有 \(a\) 个 \(1\)，\(b\) 个 \(0\)；点集 \(B\) 中有 \(c\) 个 \(1\)，\(d\) 个 \(0\)。要是按照 \(AB\) 的方式拼接，所形成的逆序对数量是 \(ad\)，若按照 \(BA\) 的方式拼接，所形成的逆序对数量是 \(bc\)。我们要是想让 \(A\) 拼接在 \(B\) 的前面，那么必须满足 \(ad < bc\)，移项可得 \(\frac{a}{b} < \frac{c}{d}\)。
所以，我们把所有点集 \(1\) 的数量除以 \(0\) 的数量再进行选择即可。

分治

xby：分治，就是把一个东西劈成两部分，左边搞一下，右边搞一下就可以了。

来看一道题：SP32079 ADAGF - Ada and Greenflies。

xby：这道题有一万种解法

我们考虑一段区间 \([l, r]\)，取中点 \(mid = \frac{l + r}{2}\)。我们注意到一个 \(mid\) 确定后，gcd 的数值只会变化 \(\log w\) 次，所以我们维护从 \(mid\) 到 \(r\) 的所有 gcd 的值再暴力匹配即可。
再来一个？
来看看P3350 [ZJOI2016] 旅行者。
我们考虑 \((x1, y1)\) 和 \((x2, y2)\) 是否在当前矩阵的左右两侧，对其进行分治处理。对于起点 \(A\) 和终点 \(B\) 以及中间点 \(C\)，答案是就是 \(dis_{AC} + dis_{CB}\).
Day1 最后一道啦：AT_abc282_h [ABC282Ex] Min + Sum。
我们设 \(s_i\) 表示数组 \(b\) 的前缀和。那么我们可以得到 \(s_r - s_{l - 1 } + a_x \le S\) 的不等式，其中 \(x\) 表示 \([l, r]\) 当中最小数的下标。
我们发现，因为 \(b_i\) 都是非负的，所以 \(s_i\) 肯定是不降的，所以我们对不等式进行变形，就可以满足一定的单调性。此时我们需要注意，如果 \(x - l + 1 \le r - x\) 的话，我们要对 \(l\) 进行枚举，否则对 \(r\) 进行枚举。
假设我们枚举 \(l\)，那么我们可以得到 \(s_r + a_x - S \le s_{l - 1}\) 的不等式，然后我们可以用二分来确定 \(l\) 的范围。
至于 \(x\) 怎么求，我们可以使用 st表。

Day 2

线段树

xby:要练习数据结构，我上初三的时候天天写。

好吧，线段树是个好东西。

线段树例题

来看一个经典的线段树题目：P4513 小白逛公园。
我们来思考一下，一段区间 \([l, r]\) 的最长子段和，有以下几种情况：

1. 由区间 \([l, mid]\) 的最长子段和；
2. 由区间 \([mid + 1, r]\) 的最长子段和；
3. 由 \(mid\) 向 \(l\)、\(r\) 两端扩展得到的；
4. \([l, mid]\) 的区间和加上 \([mid + 1, r]\) 的最大前缀和；
5. \([mid + 1, r]\) 的区间和加上 \([l, mid]\) 的最大和后缀和。

知道了这些，我们开始发扬人类智慧，本着没有困难要制造困难的原则，我们可以发现，要是想维护跨过中间的 \(mid\) 的最大子段和，那么就需要维护 \([l, mid]\) 和 \([mid + 1, r]\) 的最大子段和、最大后缀和、最大前缀和、

本题趣事：
xby现场写线段树，并且自豪的问：大家觉得能过吗？
过了 \(4\) 次提交之后，终于通过了。
lzy: NOI退役金牌就是菜啊！

来一道有点数学的OI题：
P6327 区间加区间 sin 和。
我们来看，首先我们知道：

\[\sin(a + b) = \sin a \cos b + \cos a \sin b \]

\[\cos (a + b) = \cos a \cos b - \sin a \sin b \]

然后我们根据这个公式进行展开再维护即可。

来一道难题：
P2824 [HEOI2016/TJOI2016] 排序：
这道题的难度不在于它的诡异操作，而是对于这个问题进行转化。
我们考虑一个二分，如果所有 大于 \(mid\) 的数记为 \(1\)，剩下的数记为 \(0\)。
这样我们进行 \(m\) 次排序后，\(q\) 位置上的数是 \(0\) 还是 \(1\) 进行一些判断。
这样就回到了我们熟悉的线段树区间覆盖和线段树修改问题了。

势能分析

首先，我们来看区间除、区间求和。
我们定义一个区间 \([l, r]\) 的势能 \(E = \log(a_i)\)，其中 \(a_i\) 表示区间 \([l, r]\) 中最大的数。我们会发现，最多执行 \(E\) 次后，整个区间就变成了 \(0\) 了。
所以，我们可以计算出这个程序的复杂度：\(T(2n \log(V) + n \log n)\)，化成大O表示法就是 \(O(n(\log(V) + \log(n)))\) 这样的东西。

平衡树

xby:平衡树这种东西在我的现役时期是一次也没有考过的。

因为平衡树从来不考几乎很少考，所以 xby 因为懒给我们讲解了非旋转 Treap。
首先，对于一个节点 \(pos\)，维护一下一些东西：
左右儿子，它自己的值，以及一个随机权值。
我们开始发扬人类智慧，将二叉搜索树和堆（大根堆小根堆都可以）结合起来，使得 \(v_{pos} > v_{lson_{pos}}\) 且 \(v_{pos} < v_{rson_{pos}}\)，同时还得满足 \(rnd_{pos} < rnd_{lson_{pos}}\) 以及 \(rnd_{pos} < rnd_{rson_{pos}}\)。
现在，我们开始 Treap 的核心操作：split（分裂）和 merge （合并）。

split

将一个数分裂成两个数。
我们可以发现，如果 \(pos\) 的权值要小于 \(x\) 的话，我们将 \(pos\) 的右儿子再进行分裂，将右儿子分裂完的左边的作 \(pos\) 的右儿子。反之，同理。

merge

合并操作。这个
我们可以把两个树的顶点分别设为 \(pos1\) 和 \(pos2\)。因为我们维护的是小根堆，所以我们把小的放到顶点上。
假设我们放的是 \(pos1\)，那么我们只需要把 \(pos1\) 的左儿子和 \(pos2\) 再进行合并即可。
若取的是 \(pos2\) 同理。

练习一下：P3391 【模板】文艺平衡树。
我们会思考：这和 Treap 有啥关系？
首先，我们可以把 Treap 的中序遍历视作是整个数组，那么我们对于 \([l, r]\) 进行交换（指两个儿子交换位置，以此类推）。
我们借鉴一下线段树的懒标记，设 \(tag\) 表示操作了多少次。所以，我们这里得加一个 pushdown 函数，对于 \(tag\) 传递给两个儿子。这样，这道题就迎刃而解。

Day 3

我妈：今天是NOI day2，也就是说，今天过完之后，明年的教练就出来了。

KMP

我是不会靠诉你我学过但是我忘了

xby:字符串要么大家都会，要么大家都不会。

来一道试题？
P4391 [BalticOI 2009] Radio Transmission 无线传输。
我们设 \(s_1\) 是由 \(s_2\) 重复 \(m\) 遍形成的，则 \(s_1\) 一定包含 \(s_2\) 重复 \(m - 1\) 次形成的字符串。所以，我们跑一下 KMP 算法的匹配 \(next\) 数组，答案自然就是 \(|s_1| - next_{|s_1|}\)。
来一道板子题：P4824 [USACO15FEB] Censoring S。
我们发现，每次我们删除一个 \(i\) 以后，\(i + 1\) 的 \(next_{i + 1}\) 会变成与 \(next_j\) 有关的数值。所以，每次我们删除一段之后，都会更新答案，用栈来记录一下就可以。

来道难点的？
ok，我们来看看 P3426 [POI 2005] SZA-Template。
这道题目的难度在于将 DP 与字符串结合起来。
我们不妨设 \(dp_i\) 表示 \(i\) 的前缀的答案。很明显，\(dp_i\) 有且仅有两种取值：\(i\) 或 \(dp_{next_i}\)。
什么时候 \(dp_{next_i}\) 呢？
因为 \(i\) 的后缀字符为 \(next_i\)，所以当且仅当存在一个 \(j\) 使得

\[dp_j = dp_{next_i} \]

并且，我们要求： \(i - next_i \le j\)。
所以，我们求出了 \(dp_i\) 之后要记录一下，可以使用桶，也可以使用 map。

字典树

mlh：\(1s\) 能过 \(10^5\)，那么 \(2s\) 能过 \(10^{10}\)！
xby：不，这不能。

我们来看一道经典题目：P3065 [USACO12DEC] First! G。
我们来考虑，如果我们假设 \(s\) 能被设置为最小的，那么对于 \(s\) 上的每个点 \(p\) 都和它的兄弟节点连一条有向边，再跑一边拓扑排序，看看有没有合法的拓扑排序。然后呢，没了。

来看一道P4551 最长异或路径。
我们考虑把每一条边加入一个 01Trie 树当中，依次询问每一个节点，然后通过 01Trie 树当中进行 query 查询，然后就没了。

本题趣事：
xby 心血来潮，手搓，然后先 CE，后 RE。

DP

lzy：感觉 mzh 加上 xby 都不如玄晔。

有一些神奇的DP。

背包DP

mzh：众所周知，什么01背包，完全背包，分组背包

我们来看一个与众不同的：P4141 消失之物。
我们来思考一下，对于第 \(i\) 个物品，假设我们最后把他放进背包中，那么我们可以得到一个 \(f_j\) 和 \(g_j\) 之间的数量关系：

\[f_j = g_j + g_{j - w}，w \le j \]

\[f_j = g_j，w > j \]

那么，对于 \(j < w\) 的 \(g_j\) 可以直接从 \(f_j\) 转移过来，否则我们可以递推把剩下的 \(g_j\) 求出来。

来一道好玩的：CF1442D Sum。
我们会发现，如果直接 DP 的复杂度会爆炸。我们不妨来点儿好玩的：
考虑神奇的分治，我们对于 \([l, r]\) 之间的每一个序列，我们会发现一个好玩的性质：最多就只有一个没被删干净。怎么证明？
因为每个序列都是单调不降的，所以我们假设取了某一个数列的前 \(x\) 项和另一个数列的前 \(y\) 项，且 \(w_x < w_y\) 由于每个序列都是单调不降的，所以我们把第 \(x\) 项丢掉，改选第 \(y + 1\) 项，这样一定是会优于原来的结果。
所以我们考虑第 \(mid\) 项删除了一部分，对于区间 \([l, r]\)，我们先考虑将 \([l, mid]\) 项数列都计算一下贡献，然后我们分治 \([mid + 1, r]\) 之间的每一项去寻找被我们假设删除的那一项。

看一下：P6189 [NOI Online #1 入门组] 跑步。我们考虑：
对于每一个数都小于 \(\sqrt n\) 的数，由于它的高度不够，所以它的个数会很长；相反，如果对于高度大于 \(\sqrt n\) 的每一个数，由于它的高度很高，所有他的个数自相应减少。看到没有，两个错误的解法竟然凑出了正解。