LR(逻辑回归)分类算法

一、算法原理

LR算法：通过线性映射和sigmoid转换确定{0,1}间条件概率。

1.1 模型表达(Objective Function)

逻辑回归也被称为对数几率回归，用条件概率分布的形式表示 P(Y|X)，这里随机变量 X 取值为 n 维特征向量，例如x=(x(1),x(2),...,x(n))x=(x(1),x(2),...,x(n))。

当Y 取值为 1时：

                           

当Y 取值为 0时：

                          

 等价地，对于z=w^Tx+b，通过Sigmoid函数实现实数值z到0/1值概率的转化：

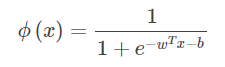                                  or                   

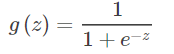
1.2 损失函数(Cost Function)

1.3 模型求解

二、超参数(结合sklearn. linear_model.LogisticRegression)

2.1 penalty(正则化策略, default ='l2' )

如果为'l2'，则优化目标函数为：为极大似然函数。

如果为'l1'，则优化目标函数为：为极大似然函数。

2.2 c(惩罚系数, default = 1)

c指定了惩罚系数的倒数。如果它的值越小，则正则化越大。

2.3 solver(最优化算法,default=’liblinear’）

'newton-cg'：使用牛顿法。

'lbfgs'：使用L-BFGS拟牛顿法。

'sag'：使用 Stochastic Average Gradient descent 算法。

'saga'：

'liblinear' ：使用 liblinear。

 注意：对于规模小的数据集，'liblearner'比较适用；对于规模大的数据集，'sag'比较适用；'newton-cg'、'lbfgs'、'sag' 只处理penalty=‘12’的情况；‘saga’ 和‘liblinear’ 可处理两种情况；

2.4 max_iter(最大迭代次数, default=100)

三、 算法优缺点

3.1 效率高

3.2 可解释性

 四、超参数调整

log_reg_params = [{'penalty': ['l1'], 
                   'C': [0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09],
                   'solver': ['saga','liblinear'],
                   'max_iter': list(range(50,550,50))},
                  {'penalty': ['l2'], 
                   'C': [0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09],
                   'solver': ['saga','liblinear','newton-cg'，'lbfgs'，'sag'],
                   'max_iter': list(range(50,550,50))}]
grid_log_reg = GridSearchCV(LogisticRegression(n_jobs=-1), log_reg_params, scoring='roc_auc') 
grid_log_reg.fit(X_train, y_train) 
log_reg = grid_log_reg.best_estimator_ 
print(log_reg) 
log_reg_score = cross_val_score(log_reg, X_train, y_train, cv=5, scoring='roc_auc') 
log_reg.fit(X_train,y_train) 
print('Logistic Regression Cross Validation Auc Score', str(log_reg_score.mean())[:6], 
      'and test Auc Score', str(roc_auc_score(y_test, log_reg.predict_proba(X_test)[:, 1]))[:6])