论文解读（WIND）《WIND: Weighting Instances Differentially for Model-Agnostic Domain Adaptation》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：WIND: Weighting Instances Differentially for Model-Agnostic Domain Adaptation
论文作者：
论文来源：2021 ACL
论文地址：download 
论文代码：download
视屏讲解：click

1 介绍

　　出发点：传统的实例加权方法由于不能学习权重，从而不能使模型在目标领域能够很好地泛化；

　　方法：为了解决这个问题，在元学习的启发下，将领域自适应问题表述为一个双层优化问题，并提出了一种新的可微模型无关的实例加权算法。提出的方法可以自动学习实例的权重，而不是使用手动设计的权重度量。为了降低计算复杂度，在训练过程中采用了二阶逼近技术；

　　贡献：

• • 提出了一种新的可微实例加权算法，该算法学习梯度下降实例的权重，不需要手动设计加权度量；
  • 采用了一种二阶近似技术来加速模型的训练；
  • 对三个典型的NLP任务进行了实验：情绪分类、机器翻译和关系提取。实验结果证明了该方法的有效性；

2 相关

　　事实：把域外、域内数据联合训练做领域适应，但并不是所有来自域外数据集的样本在训练过程中都具有相同的效果。一些关于神经机器翻译（NMT）任务的研究表明，与域内数据相关的域外实例是有益的，而与域内数据无关的实例甚至可能对翻译质量有害 。

　　目前的实列加权方法：

• • 核心思想：根据实例的重要性以及与目标域的相似性来加权实例；
  • 问题：当前领域适应场景中，域外语料库的规模大于域内语料库，容易导致学习到的权值偏向于域外数据，导致域内数据的性能较差；

3 方法

 　　为避免域内数据的性能较差，如何有效地利用 $\mathcal{D}_{\text {in }}$ 是域转移的关键。为解决这个问题，首先从 $\mathcal{D}_{\text {in }}$ 中抽取子集 $\mathcal{D}_{i t}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n_{1}}$，并为每个实例 $\left(x_{i}, y_{i}\right) \in \mathcal{D}_{i t} \cup \mathcal{D}_{\text {out }}$ 分配一个标量权值 $w_{i}$。本文希望在训练过程中，模型能够找到最优的权重 $\boldsymbol{w}=\left(w_{1}, \ldots, w_{n_{1}+m}\right)$，因此，权重 $w$ 是可微的，并可通过梯度下降优化。此外，将 DNN 表示为由 $\theta$ 参数化的函数 $f_{\theta}: \mathcal{X} \rightarrow \mathcal{Y}$，并将 $x_{i}$ 从输入空间映射到标签空间。

　　最终训练损失遵循一个加权和公式：

　　　　$\mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})=\frac{1}{n_{1}+m} \sum_{\substack{\left(x_{i}, y_{i}\right) \;\in \; \mathcal{D}_{i t}\; \cup\; \mathcal{D}_{\text {out }}}} \; w_{i} \ell\left(f_{\boldsymbol{\theta}}\left(x_{i}\right), y_{i}\right)$

　　其中 $\ell$ 表示损失函数，可以是任何类型的损失，如分类任务的交叉熵损失，或标签平滑交叉熵损失。

　　由于域内和域外数据集的数据分布存在差异，简单联合优化 $\boldsymbol{\theta}$ 和 $\boldsymbol{w}$ 可能会对 $\boldsymbol{w}$ 引入偏差。本文期望在 $\boldsymbol{w}$ 上训练的模型可以推广到域内数据。受 MAML 的启发，本文建议从 $\mathcal{D}_{i n}$ 中采样另一个子集 $\mathcal{D}_{q}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n_{2}}$ 命名为查询集，使用这个查询集来优化 $\boldsymbol{w}$。具体来说，目标是得到一个权重向量 $w$ 减少 $\mathcal{D}_{q}$ 上的损失：

　　　　$\mathcal{L}_{q}(\boldsymbol{\theta})=\frac{1}{n_{2}} \sum_{\left(x_{i}, y_{i}\right) \in \mathcal{D}_{q}} \ell\left(f_{\boldsymbol{\theta}}\left(x_{i}\right), y_{i}\right)$

　　总结：随机初始化 $\boldsymbol{w}$，用 $\mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})$ 训练一个模型，得到优化后的参数 $\boldsymbol{\theta}^{*}$，接着固定 $\boldsymbol{\theta}^{*}$ ，最小化在查询集上的损失，得到新的 $\boldsymbol{w}$。

　　该过程表述为以下双层优化问题：

　　　　$\begin{array}{ll}\underset{\boldsymbol{w}}{\text{min}}& \mathcal{L}_{q}\left(\boldsymbol{\theta}^{*}\right) \\\text { s.t. } & \boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \min }\; \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})\end{array}$

　　上述双层优化问题由于求解复杂性高，难以直接解决。受 MAML 中的优化技术启发，将每次迭代的训练过程分为以下三个步骤：

• 伪更新

　　　　$\widehat{\boldsymbol{\theta}}=\boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})$

• 实例权重更新

　　　　$\begin{aligned}\boldsymbol{w}^{*} & =\underset{\boldsymbol{w}}{\arg \min } \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}}) \\& =\underset{\boldsymbol{w}}{\arg \min } \mathcal{L}_{q}\left(\boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})\right)\end{aligned}$

　　　　$\widehat{\boldsymbol{w}}=\boldsymbol{w}-\gamma \cdot \nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}})$

• 最终更新

　　　　$\boldsymbol{\theta} \leftarrow \boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \widehat{\boldsymbol{w}})$

　　对 $\nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}})$ 使用链式法则：

　　　　$\begin{aligned}\widehat{\boldsymbol{w}} & =\boldsymbol{w}-\gamma \cdot \nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}}) \\& =\boldsymbol{w}-\gamma \cdot \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{w}} \widehat{\boldsymbol{\theta}} \\& =\boldsymbol{w}+\beta \gamma \cdot \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }}\end{aligned}$

　　问题：使用 $|\boldsymbol{\theta}|$，$|\boldsymbol{w}|$ 分别表示 $\boldsymbol{\theta}$，$\boldsymbol{w}$ 的维数，二阶推导 $\nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }}$ 是一个 $|\boldsymbol{\theta}| \times|\boldsymbol{w}|$ 矩阵，无法计算和存储。幸运的是，可采用 DARTS 中使用的近似技术来解决这个问题，这种技术使用了有限差分近似：

　　　　$\begin{array}{c}\nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }} \approx \frac{\nabla_{\boldsymbol{w}} \mathcal{L}_{\text {train }}\left(\boldsymbol{\theta}^{+}, \boldsymbol{w}\right)-\nabla_{\boldsymbol{w}} \mathcal{L}_{\text {train }}\left(\boldsymbol{\theta}^{-}, \boldsymbol{w}\right)}{2 \epsilon} \\\boldsymbol{\theta}^{+}=\boldsymbol{\theta}+\epsilon \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \\\boldsymbol{\theta}^{-}=\boldsymbol{\theta}-\epsilon \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \\\end{array}$

　　其中 $\epsilon$ 是一个小标量，设置 $\epsilon=0.01 /\left\|\nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q}\right\|_{2}$

算法

　　

4 实验

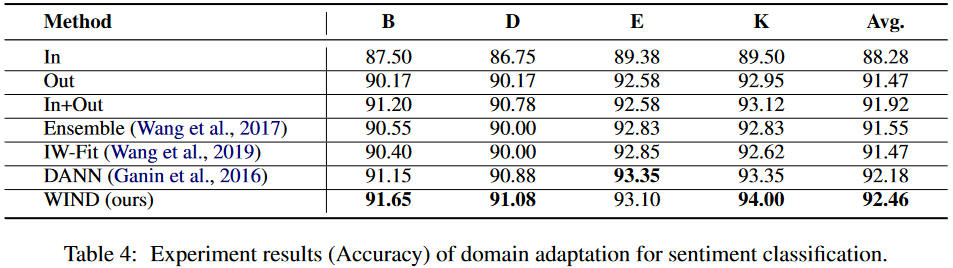
情感分析