论文解读《Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning》

论文信息

论文标题：Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning
论文作者：Qimai Li, Zhichao Han, Xiao-Ming Wu
论文来源：2018, AAAI
论文地址：download 
论文代码：download

1 Introduction

　　======================== 顶级好文 ===========================

　　贡献：

• • 证明了GCN 是拉普拉斯平滑的一种形式；
  • 从 co-taining 和 self-training 方法解决 GCN 层数多性能下降的问题；

　　虽然 平滑有助于简化分类任务，但是当 GCN 很深时，容易出现输出特征过度平滑，即来自不同簇的顶点可能会变得难以区分。如 Fig. 2 所示：

　　

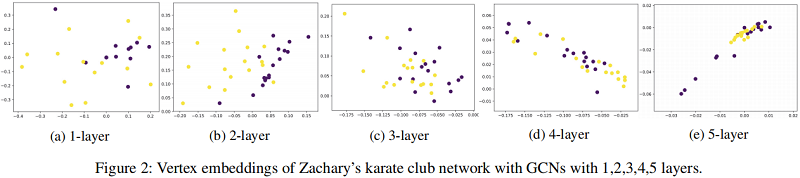
　　浅层 GCN 存在问题：它需要许多额外的标签来进行验证，此外还遭受卷积核的局部特性的问题。

　　当只给出少量标签时，浅层GCN不能有效地将标签传播到整个数据图。如图1所示，随着训练规模的缩小，GCN 的性能迅速下降，即使是那些有 500 个额外标签进行验证的也是如此。

　　

　　思考：为什么加不加验证集对于测试集精度有所影响？

Label propagation

　

　　$\mathbf{W}_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}}\quad\quad\quad(11.1)$

　　为了解决GCN存在的问题，本文提出：

• • co-training：一个基于随机游走的模型，可以对GCN补充全局信息；
  • self-training：通过对GCN的自训练，我们可以利用其特征提取能力来克服其局部性；

　　如 Fig. 1 所示，证明了本文策略的有效性。

2 Review

　　GCN 的传播过程：

　　　　$H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} \Theta^{(l)}\right) \quad\quad\quad(4)$

　　半监督节点分类：

　　　　$Z=\operatorname{softmax}\left(\hat{A} \operatorname{Re} L U\left(\hat{A} X \Theta^{(0)}\right) \Theta^{(1)}\right) \quad\quad\quad(5)$

　　对应的损失函数：

　　　　$\mathcal{L}:=-\sum_{i \in \mathcal{V}_{l}} \sum_{f=1}^{F} Y_{i f} \ln Z_{i f} \quad\quad\quad(6)$

　　其中

• • $F$ 代表着输出特征的维度；
  • $Y \in R^{\left|\mathcal{V}_{l}\right| \times F}$ 是标签矩阵；

3 Analysis

3.1 Why GCNs Work

　　不使用结构信息的 FCN 和 GCN 的在 Cora 数据集上的节点分类结果：

　　

　　全连接网络 FCN：

　　　　$H^{(l+1)}=\sigma\left(H^{(l)} \Theta^{(l)}\right) \quad\quad\quad(7)$

　　GCN 可以看成两步：

• • 首先，利用 $ X $ 获得的新特征矩阵 $Y$：$Y=\tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2} X  \quad\quad\quad(8)$ ；
  • 其次，将上述的特征矩阵  $Y$ 放入 FCN；

　　 结论：考虑结构信息的 GCN 显著好于 不考虑结构信息的 FCN。 

Laplacian Smoothing

　　拉普拉斯平滑方程：

　　　　$\hat{\mathbf{y}}_{i}=(1-\gamma) \mathbf{x}_{i}+\gamma \sum_{j} \frac{\tilde{a}_{i j}}{d_{i}} \mathbf{x}_{j} \quad(\text { for } 1 \leq i \leq n)   \quad\quad\quad(9)$

　　其中：

• • $\tilde{A}=A+I$；
  • $0<\gamma \leq 1$ 是控制当前节点和其他节点特征的权重参数；

　　重写上述 $\text{Eq.9}$ 得到：

　　　　$\hat{Y}=X-\gamma \tilde{D}^{-1} \tilde{L} X=\left(I-\gamma \tilde{D}^{-1} \tilde{L}\right) X \quad\quad\quad(10)$

 　　其中，$\tilde{L}=\tilde{D}-\tilde{A}$ 。

　　当设置 $\gamma=1$ 时，可以得到 $\hat{Y}=\tilde{D}^{-1} \tilde{A} X $ ，此时只考虑了邻居信息。

　　设置 $\gamma=1$，使用对称标准化拉普拉斯 $\tilde{D}^{-\frac{1}{2}} \tilde{L} \tilde{D}^{-\frac{1}{2}}$ 替换标准化拉普拉斯矩阵 $\tilde{D}^{-1} \tilde{L}$，可得$\hat{Y}=\tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2} X$ ，这正是$\text{Eq.8}$ 中的图卷积 。可以分别称之为 Laplacian smoothing 或者 symmetric Laplacian smoothing 。

　　Note：这里的平滑仍然包括当前顶点的特征，因为每个顶点都有一个自循环，并且是它自己的邻居。

　　为什么常说平滑有助于分类：拉普拉斯平滑法计算出一个顶点的新特征作为其自身及其邻居的加权平均值。由于同一簇中的顶点往往是紧密连接的，平滑使得它们的特征相似，这使得后续的分类任务更加容易。从 Table 1 中可以看出，只应用一次平滑已经带来了巨大的性能提高。

回顾

　　GCN 的消息传递模板：

　　　　$\mathbf{x}_{i}^{\prime}=\boldsymbol{\Theta}^{\top} \sum\limits _{j \in \mathcal{N}(v) \cup\{i\}} \frac{e_{j, i}}{\sqrt{\hat{d}_{j} \hat{d}_{i}}} \mathbf{x}_{j}$

　　APPNP ：

　　　　$\boldsymbol{Z}^{(k+1)}=(1-\alpha) \hat{\tilde{A}} \boldsymbol{Z}^{(k)}+\alpha \boldsymbol{H}$

　　随机游走：

　　

Multi-layer Structure

　　从 Table 1 中我们还可以看出，虽然 2 层FCN仅比 1 层FCN略有改善，但 2 层GCN比 1 层GCN有很大的提高。这是因为对第一层的激活再次应用平滑会使同一集群中的顶点的输出特征更加相似，并进一步简化了分类任务。

3.2 When GCNs Fail

　　下面，将证明通过多次重复应用拉普拉斯平滑，图中每个连通分量内的顶点的特征将收敛到相同的值。对于对称拉普拉斯平滑的情况，它们将收敛到与顶点度的平方根成正比。

　　假设一个图 $G$ 有 $k$ 个连通分量 $\mathcal{G}$，并且第 $i$ 个分量的指示向量用 $\left\{C_{i}\right\}_{i=1}^{k}$ 表示。该向量表示一个顶点是否在分量 $C_{i}$ 中，即：

　　　　$\mathbf{1}_{j}^{(i)}=\left\{\begin{array}{l}1, v_{j} \in C_{i} \\0, v_{j} \notin C_{i}\end{array}\right.  \quad\quad\quad(11)$

　　Theorem 1. If a graph has no bipartite components, then for any  $\mathbf{w} \in \mathbb{R}^{n}$ , and  $\alpha \in(0,1]$ ,

　　　　$\begin{array}{l}\underset{m \rightarrow+\infty}{\text{lim}}  \left(I-\alpha L_{r w}\right)^{m} \mathbf{w}=\left[\mathbf{1}^{(1)}, \mathbf{1}^{(2)}, \ldots, \mathbf{1}^{(k)}\right] \theta_{1} \\\underset{m \rightarrow+\infty}{\text{lim}}\left(I-\alpha L_{s y m}\right)^{m} \mathbf{w}=D^{-\frac{1}{2}}\left[\mathbf{1}^{(1)}, \mathbf{1}^{(2)}, \ldots, \mathbf{1}^{(k)}\right] \theta_{2}\end{array}$

　　where  $\theta_{1} \in \mathbb{R}^{k}$, $\theta_{2} \in \mathbb{R}^{k}$ , i.e., they converge to a linear combination of  $\left\{\mathbf{1}^{(i)}\right\}_{i=1}^{k}$  and  $\left\{D^{-\frac{1}{2}} \mathbf{1}^{(i)}\right\}_{i=1}^{k}$  respectively.

　　Note：由于每个顶点都添加了一个额外的自循环，所以图中没有二部分量。基于上述定理，过度平滑会使特征难以区分，损害分类精度。？？？

　　GCN 模型的问题一：如 Fig. 1 所示，随着训练规模的缩小，GCNs的性能（有无验证）迅速下降。事实上，GCN 的准确性下降的速度比标签传播的准确性要快得多。由于标签传播只使用图结构信息，而 GCNs 同时使用结构和顶点特征，这反映了GCN模型在探索全局图结构方面的无能力。

　　GCN 模型的问题二：它需要一个额外的验证集来进行训练中的早期停止，这本质上是使用验证集上的预测精度来进行模型选择。如果我们在不使用验证集的情况下对训练数据进行优化 GCN，它的性能将会显著下降。如 Fig. 1  所示，没有验集证的 GCN 的性能比有验证的 GCN 下降得明显得多。在 GCN 中，作者使用了一组额外的 500 个标记数据进行验证，这远远超过了训练数据的总数。这当然是不可取的，因为它违背了半监督学习的目的。此外，它使得 GCN 与其他方法的比较不公平，因为其他方法，如标签传播，可能根本不需要验证数据。【回答了上述 思考问题，其实我没看到这就已经想到了。】

4 Solutions

　　GCN 的优点：

• • 图卷积-拉普拉斯平滑有助于使分类问题更加容易；
  • 多层神经网络是一个强大的特征提取器；

　　GCN 的缺点：

• 图卷积是一种局部滤波器，在标记数据很少的情况下性能不佳；
• 神经网络需要大量的标记数据来进行验证和模型选择；

　　针对 GCN 的缺点，至今还有人在讨论，比如 Tangjie 教授组今年还挂了一篇论文。

4.1 Co-Train a GCN with a Random Walk Model

　　本文建议将 GCN 与随机游走模型共同训练，因为后者可以探索全局图结构，这是对GCN模型的补充。

　　特别地，我们首先使用随机游走模型来找到最自信的顶点——每个类的标记顶点的最近邻居，然后将它们添加到标签集中来训练 GCN。与 GCN 不同，我们直接优化了训练集上的 GCN 参数，而不需要额外的标记数据进行验证。

　　我们选择使用 partially absorbing random walks  (ParWalks) 作为我们的随机游动模型。ParWalks在每个状态都由部分吸收的二阶马尔科夫链。Algorithm 1 描述了使用 ParWalks 扩展标签集。

　　

　　即：

• • 首先，计算归一化吸收概率矩阵（normalized absorption probability matrix）$P=(L+\alpha \Lambda)^{-1} $，$P_{i, j}$ 是从顶点 $i$ 随机游走被顶点 $j$ 吸收的概率，它表示 $i$ 和 $j$ 属于同一类的可能性；
  • 其次，需要测量属于类 $k$ 的顶点置信度。将标记的顶点划分为 $\mathcal{S}_{1}, \mathcal{S}_{2}, \ldots$，其中 $\mathcal{S}_{k}$ 表示类 $k$ 的标记数据集。对于每个类 $k$，我们计算一个置信向量 $\mathbf{p}=\sum_{j \in \mathcal{S}_{k}} P_{:, j}$，其中 $\mathbf{p} \in \mathbb{R}^{n} $ 和 $p_{i}$ 是属于类 $k$ 的顶点 $i$ 的置信度。最后，找到 $t$ 个最自信的顶点，并将它们添加到带有标签 $k$ 的训练集中，以训练一个 GCN ；

4.2 GCN Self-Training

　　首先，使用给定的 Label 来训练 GCN，然后通过比较 softmax 的分数来挑选每个 class 中 most confident predictions，将这些数据加入到 Labeled set 之中。然后使用拓展过的数据集再次训练，初始状态使用之前 pre-trained GCN。

　　 

Combine Co-Training and Self-Training

　　为了提高 labels 的多样性和训练一个更加鲁棒的分类器，我们将 co-training 和 self-learning 结合起来。将 random walk 以及 GCN 找到的 most confidence label 加入到数据集之中，使用这些数据进一步训练 GCN。对 GCN/Random walk 找到的取交集——Union 训练方式，取并集——Intersection 训练方式。

　　看到这个不妨看看2022年 《Rethinking the Setting of Semi-supervised Learning on Graphs》，你会发现思路基本上一致。

5 Experiments

数据集

　　

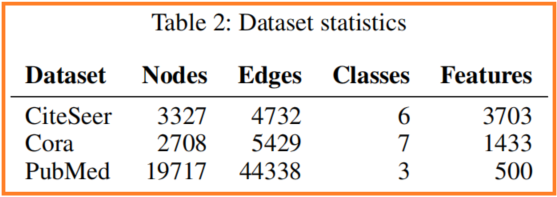
节点分类

　　

　　

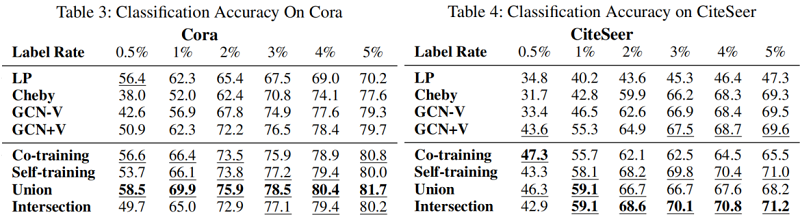
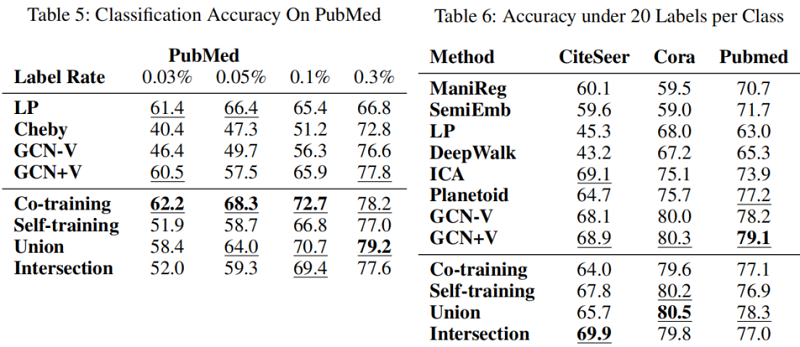
6 Conclusions

　　理解深度神经网络对于实现其在实际应用中的全部潜力至关重要。本文有助于理解GCN模型及其在半监督分类中的应用。我们的分析不仅揭示了GCN模型的机制和局限性，而且还导致了克服其局限性的新的解决方案。在未来的工作中，我们计划开发与深度架构兼容的新的卷积滤波器，并利用先进的深度学习技术来提高gcn的性能，用于更多的基于图的应用程序。

 

7 相关理论证明

证明 Theorem 1：

　　Proof.  $L_{r w}$  and  $L_{s y m}$  have the same  $n$  eigenvalues (by multiplicity) with different eigenvectors . If a graph has no bipartite components, the eigenvalues all fall in  $\left[0,2\right.  )$. The eigenspaces of  $L_{r w}$  and  $L_{s y m}$  corresponding to eigenvalue $0$ are spanned by  $\left\{\mathbf{1}^{(i)}\right\}_{i=1}^{k}$  and  $\left\{D^{-\frac{1}{2}} \mathbf{1}^{(i)}\right\}_{i=1}^{k}$  respectively. For  $\alpha \in(0,1]$ , the eigenvalues of  $\left(I-\alpha L_{r w}\right)$  and  $\left(I-\alpha L_{s y m}\right)$  all fall into  $(-1,1]$ , and the eigenspaces of eigenvalue $1$ are spanned by  $\left\{\mathbf{1}^{(i)}\right\}_{i=1}^{k}$  and  $\left\{D^{-\frac{1}{2}} \mathbf{1}^{(i)}\right\}_{i=1}^{k}$  respectively. Since the absolute value of all eigenvalues of  $\left(I-\alpha L_{r w}\right)$  and  $\left(I-\alpha L_{s y m}\right)$  are less than or equal to $1$ , after repeatedly multiplying them from the left, the result will converge to the linear combination of eigenvectors of eigenvalue $1$ , i.e. the linear combination of  $\left\{\mathbf{1}^{(i)}\right\}_{i=1}^{k}$  and  $\left\{D^{-\frac{1}{2}} \mathbf{1}^{(i)}\right\}_{i=1}^{k}$  respectively.

 

 

扯皮

　　小样本学习：从每个类中用很少的例子来学习一个分类模型。

　　正确使用无标签数据可以提高性能，2009年出现。