论文解读（MVGRL）Contrastive Multi-View Representation Learning on Graphs

论文信息

论文标题：Contrastive Multi-View Representation Learning on Graphs
论文作者：Kaveh Hassani 、Amir Hosein Khasahmadi
论文来源：2020, ICML
论文地址：download 
论文代码：download

1 Introduction

　　节点 local-global 对比学习。

2 Method

　　框架如下：

　　

　　框架由以下组件组成:

• • 仅有图结构数据增强，并无节点级数据增强；
  • 两个专用 GNN Encoder $g_{\theta}(.)$，$g_{\omega}(.)$ ；
  • 图池化层（Graph pooling layer）：即 Readout 函数；　　
  • 判别器（Discriminator）；　　

2.1 Augmentations

Graph Diffusion

　　图扩散如下：

　　　　$\mathbf{S}=\sum\limits _{k=0}^{\infty} \Theta_{k} \mathbf{T}^{k} \in \mathbb{R}^{n \times n}\quad \quad\quad(1)$

　　其中：

• • $\mathbf{T} \in \mathbb{R}^{n \times n} $ 是生成的转移矩阵，即 $\mathbf{T}=\mathbf{A} \mathbf{D}^{-1}$；　　
  • $ \Theta$  是权重系数，决定了全局和局部信息的比重；　　
  • $\sum\limits _{k=0}^{\infty} \theta_{k}=1, \theta_{k} \in[0,1] $　　
  • $\lambda_{i} \in[0,1] $ 是矩阵  $\mathbf{T} $ 的特征值，保证收敛性。　　

　　图扩散常用形式：Personalized PageRank (PPR) 和 heat kernel，定义为：

　　　　heat kernel：$\theta_{k}=e^{-t} t^{k} / k !$

　　　　PPR：$\theta_{k}=\alpha(1-\alpha)^{k}$

　　其中：$\alpha$ 表示随机游走的传送概率， $t$ 是扩散时间。

　　heat kernel 和 PPR 的扩散矩阵如下：

　　　　$\mathbf{S}^{\text {heat }}=\exp \left(t \mathbf{A} \mathbf{D}^{-1}-t\right) \quad\quad\quad\quad(2)$

　　　　$\mathbf{S}^{\mathrm{PPR}}=\alpha\left(\mathbf{I}_{n}-(1-\alpha) \mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}\right)^{-1}\quad\quad\quad\quad(3)$

Sub-sampling

　　从一个视图选择节点及其之间的边，并从另一个视图中选择一样的的节点及其之间的边。

2.2 Encoders

 　　本文采用 GCN Encoder，分别是 $g_{\theta}(.), g_{\omega}(.): \mathbb{R}^{n \times d_{x}} \times \mathbb{R}^{n \times n} \longmapsto\mathbb{R}^{n \times d_{h}}$。

　　本文将 Sub-sampling 采样的子图 和 图扩散子图看成结构一致的视图，用 GCN Encoder 提取初始节点表示：

　　　　$\sigma(\tilde{\mathbf{A}} \mathbf{X} \Theta)$

　　　　$\sigma(\mathbf{S} \mathbf{X} \Theta)$

　　其中

• • $\tilde{\mathbf{A}}=\hat{\mathbf{D}}^{-1 / 2} \hat{\mathbf{A}} \hat{\mathbf{D}}^{-1 / 2} \in \mathbb{R}^{n \times n}$；
  • $\mathbf{S} \in \mathbb{R}^{n \times n}$ 是扩散矩阵；
  • $\mathbf{X} \in \mathbb{R}^{n \times d_{x}}$ 是特征矩阵；
  • $\Theta \in \mathbb{R}^{d_{x} \times d_{h}}$ 是网络参数矩阵；
  • $\sigma$ 是非线性映射 ReLU (PReLU) ；

　　学习到的表示被喂入到共享的 MLP 映射头（2层+使用 PReLU 激活函数）：，最后生成各自对应的节点表示 

　　然后使用共享参数的 MLP $f_{\psi}(.): \mathbb{R}^{n \times d_{h}} \longmapsto \mathbb{R}^{n \times d_{h}}$ 得到最终节点表示$\mathbf{H}^{\alpha}, \mathbf{H}^{\beta} \in \mathbb{R}^{n \times d_{h}}$ 。

　　　　

---

　　为得 图级表示，Readout （$\mathcal{P}(.): \mathbb{R}^{n \times d_{h}} \longmapsto \mathbb{R}^{d_{h}}$）函数拼接每个 GCN 层的节点表示，然后将其送入全职共享的包含 $2$ 层隐藏层的 MLP，使获得的图表示与节点表示的维数大小一致:

　　　　$\vec{h}_{g}=\sigma\left(\|_{l=1}^{L}\left[\sum\limits _{i=1}^{n} \vec{h}_{i}^{(l)}\right] \mathbf{W}\right) \in \mathbb{R}^{d_{h}}\quad\quad\quad\quad(4)$

　　其中：

• • $\vec{h}_{i}^{(l)}$  节点  $\text{i}$  第  $\text{l}$ 层的潜在表示；　　
  • $\|$  是拼接操作；
  • $\text{L}$ 代表 $\mathrm{GCN}$  的层数；
  • $\mathbf{W} \in \mathbb{R}^{\left(L \times d_{h}\right) \times d_{h}}$  是网络权值矩阵；
  • $\sigma$ 是 PReLU 非线性映射；

　　　　

---

　　推断时，将图表示 $\vec{h}_{g}^{\alpha}, \vec{h}_{g}^{\beta} \in \mathbb{R}^{d_{h}}$，进行加和处理：

　　　　$\vec{h}=\vec{h}_{g}^{\alpha}+\vec{h}_{g}^{\beta} \in \mathbb{R}^{n} $

　　节点表示也进行加和处理：

　　　　$\mathbf{H}=\mathbf{H}^{\alpha}+\mathbf{H}^{\beta} \in \mathbb{R}^{n \times d_{h}} $

　　上述处理后的节点表示和图表示均可直接用于下游任务。

2.3 Training

　　local-global MI 交叉对比：

　　　　$\underset{\theta, \omega, \phi, \psi}{\text{max}}\frac{1}{|\mathcal{G}|} \sum\limits _{g \in \mathcal{G}}\left[\frac{1}{|g|} \sum\limits _{i=1}^{|g|}\left[\mathbf{M I}\left(\vec{h}_{i}^{\alpha}, \vec{h}_{g}^{\beta}\right)+\operatorname{MI}\left(\vec{h}_{i}^{\beta}, \vec{h}_{g}^{\alpha}\right)\right]\right]\quad\quad\quad\quad(5)$

　　其中：

• • $\theta$，$\omega$，$\phi$，$\psi$  是图编码器和映射头的参数；　　
  • $|\mathcal{G}|$  是图的数目；　　
  • $|g| $ 是节点的数目；　　
  • $\vec{h}_{i}^{\alpha}, \vec{h}_{g}^{\beta}$  是节点 $ i$  和图  $g$  在  $\alpha$, $\beta $ 视角下的表示。　　

　　　　

互信息作为为判别器　

　　$\mathcal{D}(., .): \mathbb{R}^{d_{h}} \times \mathbb{R}^{d_{h}} \longmapsto \mathbb{R}$  ，即:  $\mathcal{D}\left(\vec{h}_{n}, \vec{h}_{g}\right)=\vec{h}_{n} \cdot \vec{h}_{g}^{T} $

　　算法如下：

　　

3 Experiments

数据集

　　

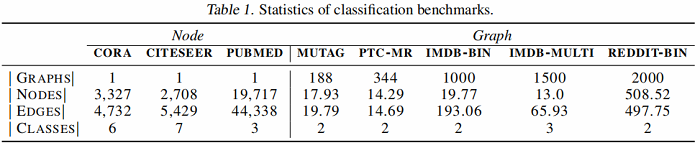
节点分类

　　

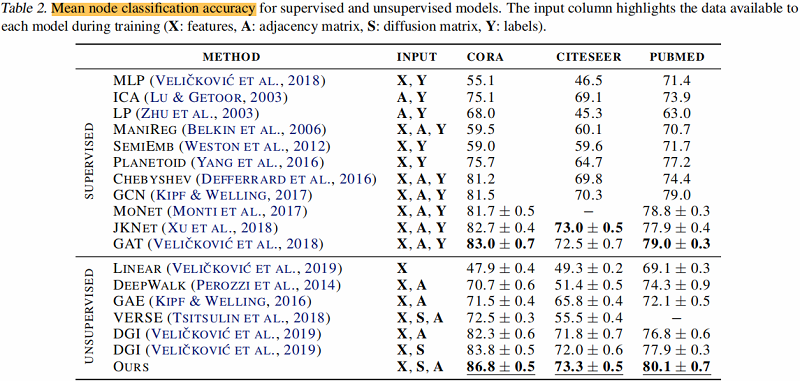
节点聚类

　　

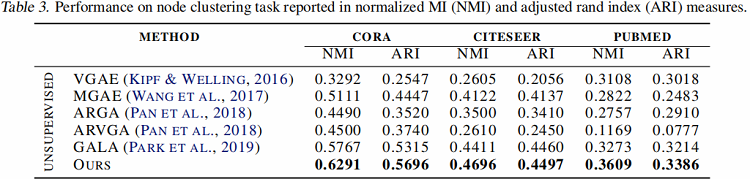
图分类

　　

互信息估计器对比

　　论文考虑了五种对比模式：

• • local-global：对比一个视角的节点编码与另一个视角的图编码；
  • global-global：对比不同视角的图编码；
  • multi-scale：对比来自一个视图的图编码与来自另一个视图的中间编码；使用 DiffPool 层计算中间编码；
  • hybrid：使用 local-global 和 global-global 模式；
  • ensemble modes：对所有视图，从相同视图对比节点和图编码。

　　

修改历史

2022-03-27 创建文章
2022-06-10 精读

论文解读目录