线性判别分析（Linear Discriminant Analysis）

1 前言

　　在学 LDA 之前，需要将其与自然语言主题模型进行区别开来。在 NLP 中， LDA 是隐含狄利克雷分布（Latent Dirichlet Allocation，简称LDA），是一种处理文档的主题模型。本文只讨论线性判别分析（LDA）。

2 LDA思想

　　基本思想：投影后类内方差最小，类间方差最大。

　　即：数据在低维度上投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

　　回顾一下主成分分析（PCA）：《机器学习——主成分分析（PCA）》

3 正文

3.1 瑞利商（Rayleigh quotient）

　　瑞利商指 $ R(A, x)$ : 

　　　　$R(A, x)=\frac{x^{H} A x}{x^{H} x} \quad \quad \quad (1)$

　　其中 $x$ 为非零向量， $A$ 为 $n \times n$  的 $Hermitan$ 矩阵（如果矩阵 $\mathrm{A}$ 是实矩阵，且满足 $A^{T}=A$ 的矩阵即为Hermitan矩阵） 。

　　瑞利商 $R(A, x) $ 的重要性质：

• 它的最大值等于矩阵 $A$  最大的特征值，而最小值等于矩阵 $A$  的最小的特征值，也就是满足

　　　　　　$\lambda_{\min } \leq \frac{x^{H} A x}{x^{H} x} \leq \lambda_{\max } \quad \quad \quad (2)$

　　  当向量 $x$ 是标准正交基时，即满足 $x^{H} x=1$ 时，瑞利商退化为:

　　　　$R(A, x)=x^{H} A x \quad \quad \quad (3)$

3.2 广义瑞利商（genralized Rayleigh quotient）

　　广义瑞利商是指这样的函数 $R(A, B, x)$  :

　　　　$R(A, B, x)=\frac{x^{H} A x}{x^{H} B x} \quad \quad \quad (4)$

　　其中  $x$  为非零向量，而  $A, B$  为  $n \times n$  的 $Hermitan$ 矩阵。  $B$  为正定矩阵。

　　思考：广义瑞利商最大值和最小值是什么呢?其形式是不是像 Eq.2 那种形式？

　　Solution：

　　通过将其标准化就可以转化为瑞利商的形式。

　　令  $x=B^{-1 / 2} x^{\prime}$ , 则分母转化为:

　　　　$x^{H} B x=x^{\prime H}(B^{-1 / 2})^{H} B B^{-1 / 2} x^{\prime}=x^{\prime H} B^{-1 / 2} B B^{-1 / 2} x^{\prime}=x^{\prime H} x^{\prime}\quad \quad \quad (5)$

　　分子则为：

　　　　$x^{H} A x=x^{\prime H} B^{-1 / 2} A B^{-1 / 2} x^{\prime}\quad \quad \quad (6)$

　　此时广义瑞利商 $R(A, B, x)$  转化为 $R\left(A, B, x^{\prime}\right)$ :

　　　　${\large R\left(A, B, x^{\prime}\right)=\frac{x^{\prime H} B^{-1 / 2} A B^{-1 / 2} x^{\prime}}{x^{\prime H} x^{\prime}}} \quad \quad \quad (7)$

3.3 二类LDA

　　数据集  $D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{m}, y_{m}\right)\right\} $，样本  $x_{i} \in \mathbb{R}^n $ ，$ y_{i} \in\{0,1\}  $。

　　如下图所示，有红蓝两种颜色标注的两个类。对于二分类问题来说，是要找一条直线，使得实列 $x_i$ 在直线上的投影尽可能的满足LDA基本思想。

　　　　

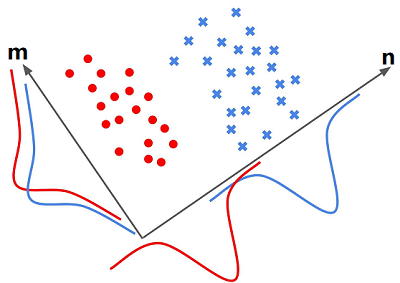
　　上图在 $m$、$n$  轴下分别有两条曲线：蓝色曲线 和 红色曲线（代表着蓝色点和红色点分别在 $m$、$n$  轴投影的密度分布函数）。

　　可以发现样本 $x_i$ 在  $n$  轴投影两个类的类间距较大（密度中心距离远），而在  $m$ 轴下的投影，类间距很小，几乎快要重合。同时也可发现，在 $n$  轴上两个类的投影密度也较 $m$  轴更大（分布的峰值更大）。显然在 $n$ 轴上满足了最大化类间方差，和最小化类内方差。

　　类内分布紧密例子：

　　　　

　　从上图，两个类在绿色线上的投影如右图所示，显然此时的投影是的类内的方差最小化，即类内分布更紧密。

　　那么得出我们的目标：找一个向量使得满足：类内更紧致，类间更远。

　　由于是两类数据，因此只需要将数据投影到一条直线上即可。这里先定义类中心：

　　　　$\mu_{j}=\frac{1}{N_{j}} \sum\limits _{x \in X_{j}} x \quad\quad(j=0,1)\quad \quad \quad (8)$

　　其中

• • $N_{j}(j=0,1) $ 为第  $j$  类样本的个数；
  • $\mu_{j}(j=0,1)$  为第 $ j  $ 类样本的均值向量；
  • $X_{j}\;(j=0,1)$ 代表 $X$ 轴下第 $j$ 类样本集合；

　　假设投影直线是向量  $w$ ，对任意一个样本  $x_{i}$ , 它在直线  $w$  的投影为 $ w^{T} x_{i}$；那么对于两个类别的中心点  $\mu_{0}$, $\mu_{1} $ ，在直线  $w$  的投影为  $w^{T} \mu_{0}$  和  $w^{T} \mu_{1} $ 。

　　LDA  需要让不同类别数据的类中心之间的距离尽可能的大（条件1：类间方差最大化），即要最大化 

　　　　 $\left\|w^{T} \mu_{0}-w^{T} \mu_{1}\right\|_{2}^{2} =w^T\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{T}w  \quad \quad \quad (9)$

　　但是不能只满足这一个条件，如下图所示，两个类在  $q$  轴上达到了类间方差最大化的条件，但在  $p$ 轴上的投影两个类重合部分太多，无法进行有效的区分。（可以理解为在 $p$ 轴方向类分布范围大，发散）

　　　　

　　所以，同时希望同一种类别数据的投影点尽可能的接近（条件2：类内方差最小化），

　　　　${\large \tilde{s}_{j}^{2}=\sum\limits _{y \in Y_{j}}\left(y-\tilde{\mu}_{j}\right)^{2}=\sum\limits_{x \in X_{j}}\left(w^{T} x-w^{T} \mu_{j}\right)^{2}=\sum\limits_{x \in X_{j}} w^{T}\left(x-\mu_{j}\right)\left(x-\mu_{j}\right)^{T} w} \quad \quad \quad (10)$

　　其中：

• • $\Sigma_{j}=\sum\limits _{x \in X_{j}}\left(x-\mu_{j}\right)\left(x-\mu_{j}\right)^{T} \quad\quad(j=0,1)$

　　故：Eq.10 等价于最小化 （2类样本）

　　　　$ w^{T} \Sigma_{0} w+w^{T} \Sigma_{1} w  \quad \quad \quad (11)$

　　综上所述，优化目标为:

　　　　${\large \underbrace{\arg \max }_{w}\; \; \; J(w)=\frac{\left\|w^{T} \mu_{0}-w^{T} \mu_{1}\right\|_{2}^{2}}{w^{T} \Sigma_{0} w+w^{T} \Sigma_{1} w}=\frac{w^{T}\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{T} w}{w^{T}\left(\Sigma_{0}+\Sigma_{1}\right) w}}  \quad \quad \quad (12)$

　　通常定义类内散度矩阵 $S_{w}$ 为:

　　　　$S_{w}=\Sigma_{0}+\Sigma_{1}=\sum\limits _{x \in X_{0}}\left(x-\mu_{0}\right)\left(x-\mu_{0}\right)^{T}+\sum\limits_{x \in X_{1}}\left(x-\mu_{1}\right)\left(x-\mu_{1}\right)^{T}\quad \quad \quad (13)$

　　类间散度矩阵 $S_{b}$ ：

　　　　$S_{b}=\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{T}\quad \quad \quad (14)$

　　那么优化目标重写为:

　　　　$\underbrace{\arg \max }_{w}\;\; J(w)={\large \frac{w^{T} S_{b} w}{w^{T} S_{w} w}} \quad \quad \quad (15)$

　　可以发现 Eq.15 就是上面将的广义瑞利商。利用广义瑞利商的性质可以知道 $J\left(w^{\prime}\right)$ 最大值为矩阵  $S_{w}^{-\frac{1}{2}} S_{b} S_{w}^{-\frac{1}{2}} $  的最大特征值，而对应的  $w^{\prime} $  为  $S_{w}^{-\frac{1}{2}} S_{b} S_{w}^{-\frac{1}{2}}$  最大特征值对应的特征向量。

　　$S_{w}^{-1} S_{b}$  的特征值和  $S_{w}^{-\frac{1}{2}} S_{b} S_{w}^{-\frac{1}{2}}$  的特征值相同， $S_{w}^{-1} S_{b} $ 的特征向量 $w$ 和 $S_{w}^{-\frac{1}{2}} S_{b} S_{w}^{-\frac{1}{2}}$  的特征向量   $w^{\prime}$   满足  $w=S_{w}^{-\frac{1}{2}} w^{\prime} $。

　　注意到二类时，  $S_{b} w$  的方向恒平行于 $ \mu_{0}-\mu_{1}$  ，不妨令  $S_{b} w=\lambda\left(\mu_{0}-\mu_{1}\right)  $，将其代入:  $\left(S_{w}^{-1} S_{b}\right) w=\lambda w$  ，可以得到  $w=S_{w}^{-1}\left(\mu_{0}-\mu_{1}\right) $ ，即只要求出原始二类样本的均值和方差就可以确定最佳的投影方向  $w $ 了。

3.4 多类LDA原理

　　数据集 $D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(\left(x_{m}, y_{m}\right)\right)\right\} $ ，其中任意样本样本  $x_{i} \in \mathbb{R}^n $ , $y_{i} \in\left\{C_{1}, C_{2}, \ldots, C_{k}\right\}$。 

　　我们定义  $N_{j}(j=1,2 \ldots k) $ 为第  $j$  类样本的个数，  $X_{j}(j=1,2 \ldots k)$  为第  $j$  类样本的集合，而  $\mu_{j}(j=1,2 \ldots k) $ 为第  $j$  类样本的均值向量，定义 $ \Sigma_{j}(j=1,2 \ldots k)$  为第  $j$  类样本的散度值。

　　由于是多类向低维投影，则此时投影到的低维空间就不是一条直线，而是一个超平面。假设投影到的低维空间的维度为  $d$ ，对应的基向量为  $\left(w_{1}, w_{2}, \ldots w_{d}\right)  $，基向量组成的矩阵为  $W$  ，它是一个  $n \times d$  的矩阵。 

　　此时优化目标应该可以变成为:

　　　　$\frac{W^{T} S_{b} W}{W^{T} S_{w} W}\quad \quad \quad (16)$

　　其中

• • $S_{b}=\sum\limits _{j=1}^{k} N_{j}\left(\mu_{j}-\mu\right)\left(\mu_{j}-\mu\right)^{T}$, $\mu$  为所有样本均值向量。 
  • $S_{w}=\sum\limits _{j=1}^{k} S_{w j}=\sum\limits_{j=1}^{k} \sum\limits_{x \in X_{j}}\left(x-\mu_{j}\right)\left(x-\mu_{j}\right)^{T}$

　　但是有一个问题，就是 $W^{T} S_{b} W$ 和 $W^{T} S_{w} W$ 都是矩阵，不是标量，无法作为一个标量函数来优化! 常见的一个LDA多类优化目标函数定义为:
　　　　$\underbrace{\arg \max }_{W} J(W)=\frac{\prod\limits _{\operatorname{diag}} W^{T} S_{b} W}{\prod\limits_{d i a g} W^{T} S_{w} W}\quad \quad \quad (17)$

　　其中 

• • $\prod\limits _{diag } A$ 为 $A$ 的主对角线元素的乘积，$ W$  为 $n \times d$ 的矩阵。 　　

　　$J(W)$ 的优化过程可以转化为：

　　　　${\large J(W)=\frac{\prod_{i=1}^{d} w_{i}^{T} S_{b} w_{i}}{\prod_{i=1}^{d} w_{i}^{T} S_{w} w_{i}}=\prod_{i=1}^{d} \frac{w_{i}^{T} S_{b} w_{i}}{w_{i}^{T} S_{w} w_{i}}} \quad \quad \quad (18)$

　　显然最右边就是广义瑞利商。最大值是矩阵 $S_{w}^{-1} S_{b} $ 的最大特征值，最大的 $\mathrm{d} $ 个值的乘积就是矩阵 $S_{w}^{-1} S_{b}$ 的最大的 $\mathrm{d} $ 个特征值的乘积，此时对应的矩阵 $W $ 为这最大的 $\mathrm{d}$ 个特征值对应的特征向量张成的矩阵。

　　由于 $W$ 是一个利用了样本的类别得到的投影矩阵，因此它的降维到的维度 $\mathrm{d}$ 最大值为 $\mathrm{k}-1 $ 。为什么最大维度不是类别数 $\mathrm{k}$ 呢? 因为 $S_{b}$ 中每个 $\mu_{j}-\mu$ 的秩为 $1$ ，因此协方差矩阵相加后最大的秩为 $\mathrm{k}$ (矩阵的秩小于等于各个相加矩阵的秩的和)，但是由于如果我们知道前 $\mathrm{k}-1$ 个 $\mu_{j}$ 后，最后一个 $\mu_{k}$ 可以由前 $\mathrm{k}-1$ 个 $\mu_{j} $ 线性 表示，因此 $S_{b}$ 的秩最大为 $\mathrm{k}-1$ ，即特征向量最多有 $\mathrm{k}-1$ 个。

4 LDA算法流程

　　输入: 数据集 $D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(\left(x_{m}, y_{m}\right)\right)\right\}$ , 其中任意样本 $x_{i} 为 \mathrm{n}$  维向量，$ y_{i} \in\left\{C_{1}, C_{2}, \ldots, C_{k}\right\} $， 降维到的维度 $\mathrm{d} $。
　　输出: 降维后的样本集 $D^{\prime} $
　　1) 计算类内散度矩阵 $S_{w} $
　　2) 计算类间散度矩阵 $S_{b} $
　　3) 计算矩阵 $S_{w}^{-1} S_{b} $
　　4) 计算 $S_{w}^{-1} S_{b}$  的最大的  $\mathrm{d} $ 个特征值和对应的  $\mathrm{d}$   个特征向量  $\left(w_{1}, w_{2}, \ldots w_{d}\right) $，得到投影矩阵  $\mathrm{W} W $
　　5) 对样本集中的每一个样本特征 $x_{i} $，转化为新的样本 $z_{i}=W^{T} x_{i} $
　　6) 得到输出样本集 $D^{\prime}=\left\{\left(z_{1}, y_{1}\right),\left(z_{2}, y_{2}\right), \ldots,\left(\left(z_{m}, y_{m}\right)\right)\right\}$