图神经网络基础一：傅里叶级数与傅里叶变换

图神经网络基础目录：

《图神经网络基础一：傅里叶级数与傅里叶变换》

《图神经网络基础二——谱图理论》

  论文解读GCN 1st《 Deep Embedding for CUnsupervisedlustering Analysis》

一、从简单变换到傅里叶级数

　　如下图所示，在笛卡尔坐标系中，定义一组基  $e_{x}=(1,0), e_{y}=(0,1)$  ，因此坐标系中的所有点能被一个坐标唯一地表示:

　　　　

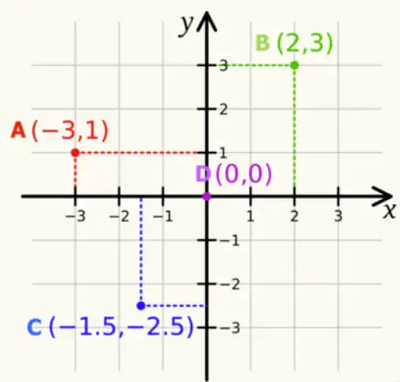
　　好处：有坐标以后，点与点之间不再是相互孤立的存在，也就有了距离的关系。这种简单的变换将空间中的点使用一组基来表示，点是基的加权累加。

　　类比到函数中，对于一个函数，期待使用一组基函数来表示。傅里叶级数与傅里叶变换就是用来解决这个问题的办法，其中傅里叶级数能够将任意周期函数表示成一组基函数依照各自的系数的累加，而傅里叶变换针对的是非周期函数。

　　首先描述傅里叶级数，它可以将任意周期函数分解为简单震荡函数（正弦函数和余弦函数等基函数) 的加和。具体地，对于周期为   $T$ 的周期函数  $f(t) $，可以分解为三角函数的组合:

　　　　$f(t)=a_{0}+\sum_{n=1}^{+\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]$

　　其中   $w=\frac{2 \pi}{T}$ ，称为基频率。类比笛卡尔坐标系， $a_{0}, a_{n}, b_{n}$   就相当于坐标，而   $1$, $\cos (n \omega t)$, $\sin (n \omega t) $  就相当于基向量。不同的是， $1, \cos (n \omega t), \sin (n \omega t) $  是一组函 数，而基向量是一组向量，笛卡尔坐标系使用基向量来表示点，傅里叶级数使用基函数来表示周期函数。

二、傅里叶级数

2.1 三角函数系

　　一个三角函数系为：

　　　　$\{1, \sin (\omega x), \cos (\omega x), \sin (2 \omega x), \cos (2 \omega x), \cdots, \sin (n \omega x), \cos (n \omega x), \cdots\}$

　　注意： $1$   也可以看做一个函数，其实也就是   $\cos (0 \omega x)$ ，由于   $\sin (0 \omega x)=0$   ，所以不考虑。

　　这里的  $ \omega$   也就是上面提到的基频率，可以看到这个基频率的大小由要分解的函数   $f(t) $  的周期   $T$   决定的，也就是说使用傅里叶级数分解周期函数时不同周期的函数要使用不同的三角函数系来作为基函数。

　　在笛卡尔坐标系中，基向量满足的性质是不同的基向量之间两两正交（内积为 0 ），相同的基向量内积为 1 。假设两个基向量   $v$   和   $ m$  ，则他们的内积就是对应的维度相乘之后的累加：

　　　　$v \cdot m=v_{1} m_{1}+v_{2} m_{2}+\cdots+v_{n} m_{n}=0$

　　傅里叶级数的基函数之间也有类似的性质，基向量之间的内积是以累加的方式计算的，类似 的，基函数之间的内积是以积分的形式计算的。同样类似的，不同基函数之间的内积为   $0$ ， 同一基函数的内积为一个正数。

知识点补充：

　　傅里叶级数的基础是三角函函数系  $1, \sin x, \cos x, \sin 2 x, \cos 2 x, \ldots, \sin n x, \cos n x$  的正交性。正交是对于线性无关的抽象概念，类比向量正交即为内积等于零的概念，函数的正交同样采用内积等于零来判断。

　　现定义两个实函数：$f(x), g(x)$ 的内积。若 $f(x), g(x)$ 在闭区间  $[a, b] $上可积且平方可积，则它们的内积：

　　　　 $<f, g>=\int_{a}^{b} f(x) g(x) \mathrm{d} x$ 

　　在$[0,2 \pi] $  上，三角函数系是两两正交的，它们满足如下性质：

　　　　$(1) \int_{0}^{2 \pi} \sin n x \mathrm{~d} x=0\left(n \in \mathbb{N}^{*}\right)$ 

　　　　$(2) \int_{0}^{2 \pi} \cos n x \mathrm{~d} x=0\left(n \in \mathbb{N}^{*}\right) $

　　　　$(3) \int_{0}^{2 \pi} \sin n x \cos m x \mathrm{~d} x=0\left(n \neq m, n \in \mathbb{N}^{*}, m \in \mathbb{N}^{*}\right) $

　　　　$(4) \int_{0}^{2 \pi} \sin n x \sin m x \mathrm{~d} x=0\left(n \neq m, n \in \mathbb{N}^{*}, m \in \mathbb{N}^{*}\right) $

　　　　$(5) \int_{0}^{2 \pi} \cos n x \cos m x \mathrm{~d} x=0\left(n \neq m, n \in \mathbb{N}^{*}, m \in \mathbb{N}^{*}\right)$

　　前两个式子显然成立，后三个式子的推导主要是利用积化和差公式，在这里给出最后一个式子的推导过程。

　　　　$\begin{array}{l}& \int_{0}^{2 \pi} \cos n x \cos m x \mathrm{~d} x \\=& \int_{0}^{2 \pi} \frac{\cos (n+m) x+\cos (n-m) x}{2} \mathrm{~d} x \\=& \frac{1}{2}\left[\frac{\sin (n+m) x}{n+m}+\frac{\sin (n-m) x}{n-m}\right]_{0}^{2 \pi} \\=& 0\end{array}$

2.2 傅里叶级数的直观理解

2.2.1 矩形波的分解

　　以一个周期矩形波为例，难以想象的是这个矩形波是可以被傅里叶级数分解的。下图中展示了多个正弦函数如何逐步组合成为一个矩形波，随着震荡函数的增加，它们最终就可以组成一个矩形波：

　　　　

　　注意这里只有正弦函数而没有余弦函数。我们之前说任意周期函数都可以由正弦和余弦函数累加而组成，而事实上我们只需要有相位的正弦函数就可以组成任意的周期函数了。下图也同样展示了这些有相位的正弦波组合成矩形波的过程：

　　　　

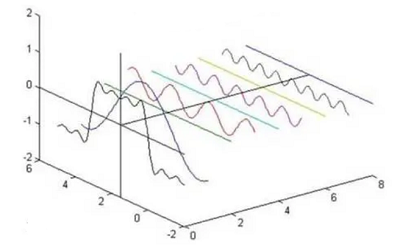
　　这里的正弦波之间还有一些直线，这些直线其实也是正弦波，只不过振幅为  $0$  ，这说明组成一个周期函数时，可能一些成分是不需要的。

2.2.2 频谱

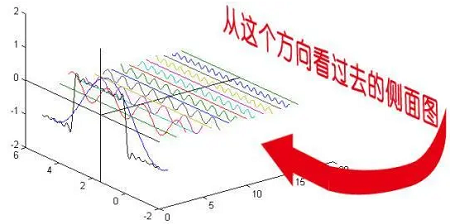
　　上面的图立体地展示了正弦波组合成周期函数的过程，如果我们从侧面来看这个立体图，也就得到了所谓的频谱（Spectrum）：

　　　　

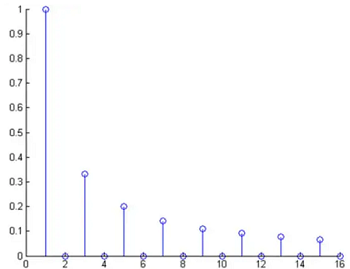
　　即：以这些正弦波的频率做横轴，振幅做竖轴得到图像：

　　　　

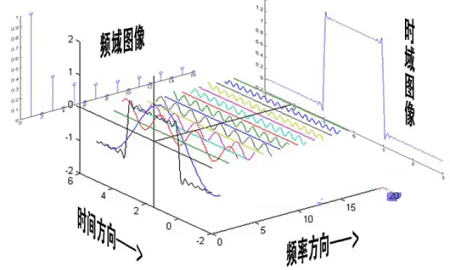
　　重新审视一个周期函数的立体分解图——>从正面来看是时域（Time Domain）的图像，从侧面就是频域（Frequency Domain）图像：

　　　　

2.2.3 相位谱

　　频谱记录了正弦波的频率和振幅，但没有记录相位信息。

　　这里以频率为横轴，相位为纵轴构建一个相位谱（phase spectrum）：

　　　　

　　利用频谱和相位谱就可以记录所有的组成一个周期函数的正弦函数了。

　　集合图：

　　　　

2.2.3 傅里叶级数的由来

　　现在解释下面式子（傅里叶级数）的由来：

　　　　$f(t)=a_{0}+\sum \limits _{n=1}^{+\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]$

　　利用带有相位的正弦函数可以组合成任意的周期函数，此时基频率还是   $\omega=\frac{2 \pi}{T} $， 该过程用公式表示为:

　　　　$f(t)=\sum\limits_{n=0}^{+\infty} A_{n} \sin \left(n \omega t+\varphi_{n}\right)$

　　利用和角公式进行一些变换:

　　$\begin{array}{l}&f(t)=\sum\limits _{n=0}^{+\infty} A_{n} \sin \left(n \omega t+\varphi_{n}\right) \\&=\sum\limits_{n=0}^{+\infty} A_{n}\left[\sin (n \omega t) \cos \left(\varphi_{n}\right)+\cos (n \omega t) \sin \left(\varphi_{n}\right)\right] \\&=\sum\limits_{n=0}^{+\infty}\left[A_{n} \cos \left(\varphi_{n}\right) \sin (n \omega t)+A_{n} \sin \left(\varphi_{n}\right) \cos (n \omega t)\right] \\&=A_{0} \cos \left(\varphi_{0}\right) \underbrace{\sin (0 \omega t)}_{=0}+\underbrace{A_{0} \sin \left(\varphi_{0}\right)}_{\text {记作 } a_{0}} \underbrace{\cos (0 \omega t)}_{=1}+\sum\limits_{n=1}^{+\infty}[\underbrace{A_{n} \cos \left(\varphi_{n}\right)}_{\text {记作 } b_{n}} \sin (n \omega t)+\underbrace{A_{n} \sin \left(\varphi_{n}\right)}_{\text {记作 } a_{n}} \cos (n \omega t)] \\&=a_{0}+\sum\limits_{n=1}^{+\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]\end{array}$

　　最终得到了上述傅里叶级数。

2.2.4 求解傅里叶级数的系数

　　对于一个周期函数    $f(t)$  ，如何求它分解为傅里叶级数后的系数  $a_{0}, a_{n}, b_{n}$  呢?

　　同样类比笛卡尔坐标系，一个坐标点与一个基向量做内积就可以得到这个坐标点在这个基向量上的系数， 那么一个周期函数只需要与一个基函数做积分，也就可以得到对应的系数。

　　首先求  $a_{0}$  (  $a_{0} $   对应的基函数为  $\cos (0 t) $ ）:

　　$\begin{array}{l}\int_{0}^{T} f(t) \cos (0 t) \mathrm{d} t&=\int_{0}^{T}\left(a_{0}+\sum \limits _{n=1}^{+\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]\right) \cos (0 t) \mathrm{d} t \\&=\int_{0}^{T} a_{0} \cos (0 t) \mathrm{d} t+\int_{0}^{T} \sum \limits_{n=1}^{+\infty}[a_{n} \underbrace{\cos (n \omega t) \cos (0 t)}_{\text {积分 } 0}+b_{n} \underbrace{\sin (n \omega t) \cos (0 t)}_{\text {积分为 } 0}] \mathrm{d} t \\&=a_{0} T\end{array}$

　　即：

　　　　$a_{0}=\frac{1}{T} \int_{0}^{T} f(t) \mathrm{d} t$

　　然后求  $ a_{n}$  ，对应的基函数为 $\cos (n \omega t)$  : 

　　　　$\begin{array}{l}&\int_{0}^{T} f(t) \cos (n \omega t) \mathrm{d} t\\&=\int_{0}^{T}\left(a_{0}+\sum \limits _{n=1}^{+\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]\right) \cos (n \omega t) \mathrm{d} t \\&=\int_{0}^{T} a_{0} \cos (n \omega t) \mathrm{d} t+\int_{0}^{T} \sum \limits_{n=1}^{+\infty} a_{n} \cos (n \omega t) \cos (n \omega t) \mathrm{d} t+\int_{0}^{T} \sum \limits_{n=1}^{+\infty} b_{n} \sin (n \omega t) \cos (n \omega t) \mathrm{d} t \\&=\int_{0}^{T} a_{n} \cos (n \omega t) \cos (n \omega t) \mathrm{d} t \\&=\int_{0}^{T} a_{n} \cos ^{2}(n \omega t) \mathrm{d} t \\&=\int_{0}^{T} a_{n} \frac{1+\cos (2 n \omega t)}{2} \mathrm{~d} t \\&=a_{n} \frac{T}{2}\end{array}$

　　即：

　　　　$a_{n}=\frac{2}{T} \int_{0}^{T} f(t) \cos (n \omega t) \mathrm{d} t$

　　最后用类似的方法求得  $b_{n}$:

　　　　$b_{n}=\frac{2}{T} \int_{0}^{T} f(t) \sin (n \omega t) \mathrm{d} t$

2.2.5 欧拉公式与傅里叶级数

　　首先有欧拉公式如下：

　　　　$e^{i \theta}=\cos (\theta)+i \sin (\theta)$

　　复变函数中，$e^{(ix)}=(cos x+isin x)$  称为欧拉公式，$e$  是自然对数的底，$i$  是虚数单位。

　　可以简单的将欧拉公式理解为复数的另一种表示形式， $e^{i \theta} $  看做复数。

　　为简化傅里叶级数的表达形式，需要用到欧拉公式。
　　当   $\theta=n \omega t $   以及  $  \theta=-n \omega t $  时，根据欧拉公式有:

　　　　$\begin{array}{l}e^{i n \omega t}=\cos (n \omega t)+i \sin (n \omega t) \\e^{-i n \omega t}=\cos (n \omega t)-i \sin (n \omega t)\end{array}$

　　那么：

　　　　$\begin{aligned}\cos (n \omega t) &=\frac{e^{i n \omega t}+e^{-i n \omega t}}{2} \\\sin (n \omega t) &=\frac{e^{i n \omega t}-e^{-i n \omega t}}{2 i}\end{aligned}$

　　将这两项代入傅里叶级数，并进行整理：

　　　　$\begin{array}{l}f(t)&=a_{0}+\sum \limits _{n=1}^{+\infty}\left[a_{n} \frac{e^{i n \omega t}+e^{-i n \omega t}}{2}+b_{n} \frac{e^{i n \omega t}-e^{-i n \omega t}}{2 i}\right] \\&=a_{0}+\sum \limits_{n=1}^{+\infty}\left(\frac{a_{n}-i b_{n}}{2}\right) e^{i n \omega t}+\sum \limits_{n=1}^{+\infty}\left(\frac{a_{n}+i b_{n}}{2}\right) e^{-i n \omega t} \\&=\sum \limits_{n=0}^{0} a_{n} e^{i n \omega t}+\sum \limits_{n=1}^{+\infty}\left(\frac{a_{n}-i b_{n}}{2}\right) e^{i n \omega t}+\sum \limits_{n=-1}^{-\infty}\left(\frac{a_{-n}+i b_{-n}}{2}\right) e^{i n \omega t} \\&=\sum \limits_{-\infty}^{+\infty} c_{n} e^{i n \omega t}\end{array}$

　　其中：

　　　　$\begin{array}{l}\text { 当 } n=0 \text { 时 }, c_{n}=a_{0} \\\text { 当 } n=1,2,3, \cdots \text { 时, } c_{n}=\frac{a_{n}-i b_{n}}{2} \\\text { 当 } n=-1,-2,-3, \cdots \text { 时, } c_{n}=\frac{a_{-n}+i b_{-n}}{2}\end{array}$

　　上一小节求得系数  $a_{0}, a_{n}, b_{n}$  ，现在将这些系数代入经过欧拉公式变换后的傅里叶级数。

　　首先，当  $n=0$  时:

　　　　$\begin{array}{l}c_{n}=a_{0} \\=\frac{1}{T} \int_{0}^{T} f(t) \mathrm{d} t \\=\frac{1}{T} \int_{0}^{T} f(t) e^{-i 0 \omega t} \mathrm{~d} t\end{array}$

　　当 $n=1,2,3, \cdots$ 时: 

　　　　$\begin{array}{l}c_{n}&=\frac{a_{n}-i b_{n}}{2} \\&=\frac{\frac{2}{T} \int_{0}^{T} f(t) \cos (n \omega t) \mathrm{d} t-i \frac{2}{T} \int_{0}^{T} f(t) \sin (n \omega t) \mathrm{d} t}{2} \\&=\frac{1}{T} \int_{0}^{T} f(t)[\cos (n \omega t)-i \sin (n \omega t)] \mathrm{d} t \\&=\frac{1}{T} \int_{0}^{T} f(t) e^{-i n \omega t} \mathrm{~d} t\end{array}$

　　可见对于任意的 $n$ ，所有的 $c_{n}$ 的表达式都是一样的。

　　总结一下，傅里叶级数最终可以写为:

　　　　$f(t)=\sum \limits_{n=-\infty}^{+\infty} c_{n} e^{i n \omega t}$

　　其中

　　　　$ c_{n}=\frac{1}{T} \int_{0}^{T} f(t) e^{-i n \omega t} \mathrm{~d} t$

　　上面的式子说明，任意一个周期为  $T$  的周期函数，都可以使用一组  $c_{n}$  来表示它。也就 是说，在时域内  $(t, f(t))$  可以唯一地确定函数  $f(t)$  ，而在频域内，函数  $f(t)$  由  $\left(n, c_{n}\right)$  来唯一确定，这就是从时域到频域的转换，如下图：

　　　　

 　　上图右边纵轴  $c_{n}$  其实是个复数，可以理解为应该有两个维度，一个实部，一个虚部，但是这 里为了简单画图，就把它画成了实数，但其实它是个复数。

三、傅里叶变换

　　傅里叶变换针对非周期函数，一个非周期函数可以看做周期无限大的函数。

　　同样的以 $\boldsymbol{\omega}$ 作为基频率，满足 $\omega=\frac{2 \pi}{T}$ ，当 $T \rightarrow+\infty$ 时， $ \omega \rightarrow 0 $ ，又有 $\omega=(n+1) \omega-n \omega=\Delta \omega $ ，因此 $\Delta \omega \rightarrow 0$ 。

　　在这里我们将 $c_{n}$ 写作从 $-\frac{T}{2}$ 到 $\frac{T}{2} $ 的积分:

　　　　$c_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-i n \omega t} \mathrm{~d} t$

　　那么对于非周期函数  $f(t)$  来说有：

　　　　$\begin{array}{l}f(t)&=\underset{T \rightarrow+\infty}{lim}    \sum \limits_{n=-\infty}^{+\infty} c_{n} e^{i n \omega t} \\&=\underset{T \rightarrow+\infty}{lim}    \sum \limits_{n=-\infty}^{+\infty} \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-i n \omega t} \mathrm{~d} t \cdot e^{i n \omega t} \\&=\underset{\Delta \omega \rightarrow 0}{lim}    \sum \limits_{n=-\infty}^{+\infty} \frac{\Delta \omega}{2 \pi} \int_{-\infty}^{+\infty} f(t) e^{-i n \omega t} \mathrm{~d} t \cdot e^{i n \omega t}\end{array}$

　　从下图中可以看做，当  $\Delta \omega \rightarrow 0$  时，虽然 $n$  为离散的量，但是  $n \omega$  会变成一个连续的量: 

　　　　

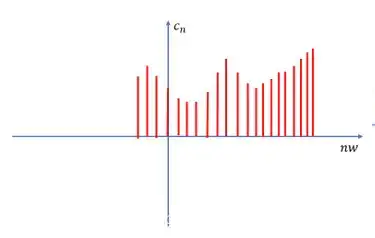
　　注意   $\Delta \omega=\omega$  ，另外我们令  $ W=n \omega$   ，那么我们有:  

　　　　$\begin{array}{l}f(t)&=\underset{\omega \rightarrow  0}{lim}  \sum \limits _{n=-\infty}^{+\infty} \frac{\omega}{2 \pi} \int_{-\infty}^{+\infty} f(t) e^{-i n \omega t} \mathrm{~d} t \cdot e^{i \pi \omega t} \\&=\int_{-\infty}^{+\infty} \frac{1}{2 \pi}\left(\int_{-\infty}^{+\infty} f(t) e^{-i W t} \mathrm{~d} t\right) e^{i W t} \mathrm{~d} W \\&=\frac{1}{2 \pi} \int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty} f(t) e^{-i W t} \mathrm{~d} t\right) e^{i W t} \mathrm{~d} W\end{array}$

　　注意这里的  $\int_{-\infty}^{+\infty} f(t) e^{-i W t} \mathrm{~d} t$  是对   $t$  进行积分，因此它是关于 $W$  的函数，定义:  

　　　　$F(W)=\int_{-\infty}^{+\infty} f(t) e^{-i W t} \mathrm{~d} t$

　　$F(W)$   就是   $f(t)$  的傅里叶变换，将 $F(W)$ 代入 $f(t)$ 得:

　　　　$f(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} F(W) e^{i W t} \mathrm{~d} W$

　　$f(t)$  就是傅里叶变换的逆变换。 

参考：

　　1、图卷积神经网络(GCN)深入理解(1) 矩阵的谱分解

　　2、图卷积神经网络课程笔记（一）——谱域图卷积（Spectral）背景知识及经典模型