论文解读(GraphSAGE)《Inductive Representation Learning on Large Graphs》
论文信息
论文标题:Inductive Representation Learning on Large Graphs
论文作者:William L. Hamilton, Rex Ying
论文来源:2017, NIPS
论文地址:download
论文代码:download
1 Introduction
创新:基于采样和聚合的算法。
1.1 Transductive Learning
即直推式学习,已经预先观察了所有数据,含训练和测试数据集。 从已经观察到的数据集中学习,然后预测测试数据集的标签。 即过程会利用这些不知道数据标签的测试集数据的模式和其他信息。

def load_inductive_dataset(dataset_name):
if dataset_name == "ppi":
batch_size = 2
# define loss function
# create the dataset
train_dataset = PPIDataset(mode='train')
valid_dataset = PPIDataset(mode='valid')
test_dataset = PPIDataset(mode='test')
train_dataloader = GraphDataLoader(train_dataset, batch_size=batch_size)
valid_dataloader = GraphDataLoader(valid_dataset, batch_size=batch_size, shuffle=False)
test_dataloader = GraphDataLoader(test_dataset, batch_size=batch_size, shuffle=False)
eval_train_dataloader = GraphDataLoader(train_dataset, batch_size=batch_size, shuffle=False)
g = train_dataset[0]
num_classes = train_dataset.num_labels
num_features = g.ndata['feat'].shape[1]
else:
_args = namedtuple("dt", "dataset")
dt = _args(dataset_name)
batch_size = 1
dataset = load_data(dt)
print("dataset = ",dataset)
num_classes = dataset.num_classes
g = dataset[0]
num_features = g.ndata["feat"].shape[1]
train_mask = g.ndata['train_mask']
feat = g.ndata["feat"]
feat = scale_feats(feat)
g.ndata["feat"] = feat
g = g.remove_self_loop()
g = g.add_self_loop()
train_nid = np.nonzero(train_mask.data.numpy())[0].astype(np.int64)
train_g = dgl.node_subgraph(g, train_nid)
train_dataloader = [train_g]
valid_dataloader = [g]
test_dataloader = valid_dataloader
eval_train_dataloader = [train_g]
return train_dataloader, valid_dataloader, test_dataloader, eval_train_dataloader, num_features, num_classes
GCN 就是一个典型的例子:

def train(epoch):
t = time.time()
model.train()
optimizer.zero_grad()
output = model(features, adj)
loss_train = F.nll_loss(output[idx_train], labels[idx_train])
acc_train = accuracy(output[idx_train], labels[idx_train])
loss_train.backward()
optimizer.step()
if not args.fastmode:
# Evaluate validation set performance separately,
# deactivates dropout during validation run.
model.eval()
output = model(features, adj)
loss_val = F.nll_loss(output[idx_val], labels[idx_val])
acc_val = accuracy(output[idx_val], labels[idx_val])
def test():
model.eval()
output = model(features, adj)
loss_test = F.nll_loss(output[idx_test], labels[idx_test])
acc_test = accuracy(output[idx_test], labels[idx_test])
缺点:一旦有新的节点出现,直推式学习需要重新训练模型。
1.2 Inductive Learning
即归纳式学习,只能使用已经观测到的数据(有标签),对于没有标签的节点在训练过程中只能忽略(不使用结构信息和属性信息)。

def load_dataset(dataset_name):
assert dataset_name in GRAPH_DICT, f"Unknow dataset: {dataset_name}."
if dataset_name.startswith("ogbn"):
dataset = GRAPH_DICT[dataset_name](dataset_name)
else:
dataset = GRAPH_DICT[dataset_name]()
if dataset_name == "ogbn-arxiv":
graph, labels = dataset[0]
num_nodes = graph.num_nodes()
split_idx = dataset.get_idx_split()
train_idx, val_idx, test_idx = split_idx["train"], split_idx["valid"], split_idx["test"]
graph = preprocess(graph)
if not torch.is_tensor(train_idx):
train_idx = torch.as_tensor(train_idx)
val_idx = torch.as_tensor(val_idx)
test_idx = torch.as_tensor(test_idx)
feat = graph.ndata["feat"]
feat = scale_feats(feat)
graph.ndata["feat"] = feat
train_mask = torch.full((num_nodes,), False).index_fill_(0, train_idx, True)
val_mask = torch.full((num_nodes,), False).index_fill_(0, val_idx, True)
test_mask = torch.full((num_nodes,), False).index_fill_(0, test_idx, True)
graph.ndata["label"] = labels.view(-1)
graph.ndata["train_mask"], graph.ndata["val_mask"], graph.ndata["test_mask"] = train_mask, val_mask, test_mask
else:
graph = dataset[0]
graph = graph.remove_self_loop()
graph = graph.add_self_loop()
num_features = graph.ndata["feat"].shape[1]
num_classes = dataset.num_classes
return graph, (num_features, num_classes)
主要观点是:节点的嵌入可以通过一个共同的聚合邻居节点信息的函数得到,在训练时只要得到这个聚合函数,就可以将其泛化到未知的节点上。
2 GraphSAGE Method
GraphSAGE 的核心思想:不是试图学习一个图上所有 Node Embedding,而是学习一个为每个 Node 产生 Embedding 的映射(即产生一个通用的映射函数)。
本文提出的 GraphSAGE(Inductive Method) 可以利用所有图中存在的结构特征(如:节点度,邻居信息),去推测未知的节点表示。
举例如下:
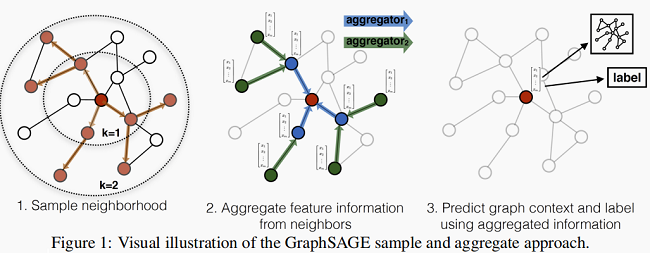
- 先对邻居随机采样,降低计算复杂度(Figure 1 :一跳邻居采样数=3,二跳邻居采样数=5)
- 生成目标节点 Emebedding:先聚合2跳邻居特征,生成一跳邻居 Embedding,再聚合一跳邻居 Embedding,生成目标节点 Embedding,从而获得二跳邻居信息。
- 将 Embedding 作为全连接层的输入,预测目标节点的标签。
2.1 Embedding generation algorithm
GraphSAGE 算法如下:

注意:$K$ 控制着跳数,本文这边取 $K=2$。
举例:
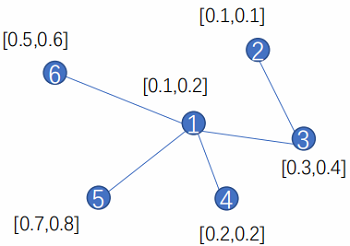
这里以节点 $1$ 为例,采用均值聚合。
对于节点 $1$ ,它相连的邻居为 ${3,4,5,6}$。(这里以聚合所有邻居信息为例)
对于算法中的第 4 步:$h_{\mathcal{N}(1)}^{1} \leftarrow A G G R E G A T E\left(\left\{h_{3}^{0}, h_{4}^{0}, h_{5}^{0}, h_{6}^{0}\right\}\right)$:
$h_{\mathcal{N}(1)}^{1}=A G G R E G A T E\left(\left\{h_{3}^{0}, h_{4}^{0}, h_{5}^{0}, h_{6}^{0}\right\}\right)=\operatorname{Mean}([0.3,0.4],[0.2,0.2],[0.7,0.8],[0.5,0.6]$
对于算法中的第 5 步:$h_{1}^{1} \leftarrow \sigma\left(W^{1} \cdot \operatorname{CONCAT}\left(h_{1}^{0}, h_{\mathcal{N}(1)}^{1}\right)\right)$ :
$\left.h_{1}^{1}=W \cdot \operatorname{CONCAT}\left(h_{1}^{0}, h_{\mathcal{N}(1)}^{1}\right)\right)=W \cdot[0.1,0.2,0.425,0.5]$
改进:聚合部分邻居
-
- 对于节点 $1$,比如我们要聚合其 $3$ 个邻居的信息,那就按均匀分布随机在其邻居集合中选择 $3$ 个邻居节点。(节点不重复)
- 对于节点 $1$,比如我们要聚合其 $6$ 个邻居的信息,那就先聚合其所有邻居一次($5$ 个邻居),然后在按均匀分布随机在其邻居集合中选择 $1$ 个邻居节点。(节点重复)
注意点:上述提到 $K$ 控制着跳数。
举例:【$K=2,S_1 =2,S_2 = 3$】
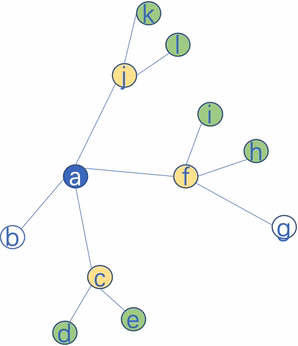
本文实验说明聚合邻居数最好满足: $S_{1} \cdot S_{2} \leq 500$。
基于 minibatch 版本的 GraphSAGE 算法:

举例:
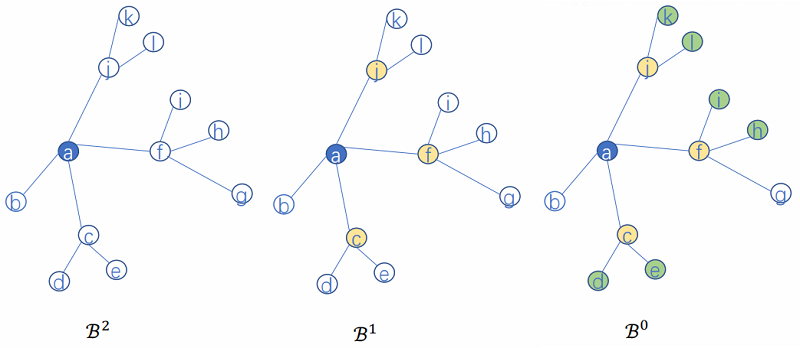
考虑:
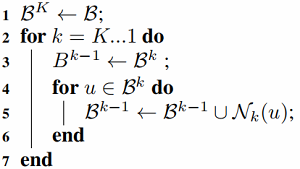
假设:$K=2, S_1=2, S_2=3$,$\mathcal{B}^{2}=\{a\}$
那么:
$\mathcal{B}^{1}=\{a\} \cup \mathcal{N}_{2}(a)=\{a\} \cup\{c, f, j\}$
$\mathcal{B}^{0}=\{a\} \cup\{c, f, j\} \cup \mathcal{N}_{1}(\{c, f, j\})=\{a\} \cup\{c, f, j\} \cup\{d, e, i, h, k, l\}$
考虑:

$\begin{array}{l}\mathcal{B}^{1}=\{a\} \cup \mathcal{N}_{2}(a)=\{a\} \cup\{c, f, j\} \\\mathcal{N}_{1}(c)=\{d, e\} \\h_{\mathcal{N}(c)}^{1} \leftarrow A G G R E G A T E_{1}\left\{h_{d}^{0}, h_{e}^{0}\right\} \\h_{c}^{1} \leftarrow \sigma\left(W^{1} \cdot \operatorname{CONCAT}\left(h_{c}^{0}, h_{\mathcal{N}(1)}^{1}\right)\right)\end{array}$
2.2 Learning the parameters of GraphSAGE
损失函数分为基于图的无监督损失和有监督损失。
- 基于图的无监督损失:目标是使节点 $u$ 与 “邻居” $v$ 的 Embedding 相似,与无边相连的节点 $v_n$ 不相似。
$J_{\mathcal{G}}\left(\mathbf{z}_{u}\right)=-\log \left(\sigma\left(\mathbf{z}_{u}^{\top} \mathbf{z}_{v}\right)\right)-Q \cdot \mathbb{E}_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-\mathbf{z}_{u}^{\top} \mathbf{z}_{v_{n}}\right)\right)$
其中:
-
- 节点 $v$ 是节点 $u$ 经过固定长度的 Random walk 到达的邻居节点;
- $v_{n} \sim P_{n}(u)$ 表示负采样:节点 $v_{n}$ 是从节点 $u$ 的负采样分布 $P_{n}$ 采样的, $Q$ 为采样样本数;
- 基于图的有监督损失:无监督损失函数的设定来学习节点 Embedding 可以供下游多个任务使用,若仅使用在特定某个任务上,则可以替代上述损失函数符合特定任务目标,如交叉熵。
2.3 Aggregator Architectures
由于节点是无序的,所以聚合器需要满足排列不变性。
排列不变性(permutation invariance):指输入的顺序改变不会影响输出的值。
- Mean aggregator
$h_{v}^{k}=\sigma\left(W^{k} \cdot \operatorname{mean}\left(\left\{h_{v}^{k-1}\right\} \cup\left\{h_{u}^{k-1}, \forall u \in N(v)\right\}\right)\right.$
- LSTM aggregator
LSTM函数不符合 "排列不变性" 的性质,需要先对邻居随机排序,然后将随机的邻居序列 Embedding $ \left\{x_{t}, t \in N(v)\right\}$ 作为 LSTM 输入。
-
Pooling aggregator
一个 element-wise max pooling 操作应用在邻居集合上来聚合信息:
$\text { AGGREGATE }_{k}^{\mathrm{pool}}=\max \left(\left\{\sigma\left(\mathbf{W}_{\text {pool }} \mathbf{h}_{u_{i}}^{k}+\mathbf{b}\right), \forall u_{i} \in \mathcal{N}(v)\right\}\right)$
$\mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W}^{k} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{v}^{k-1}, \mathbf{h}_{\mathcal{N}(v)}^{k}\right)\right)$
3 Experiments
基线实验
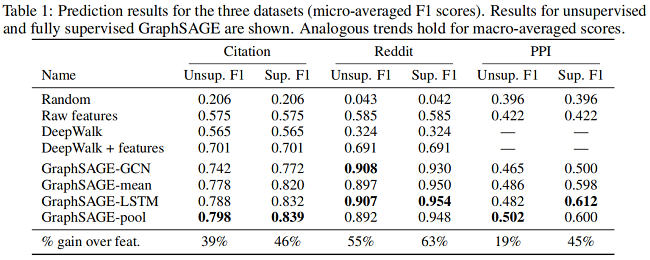
消融实验
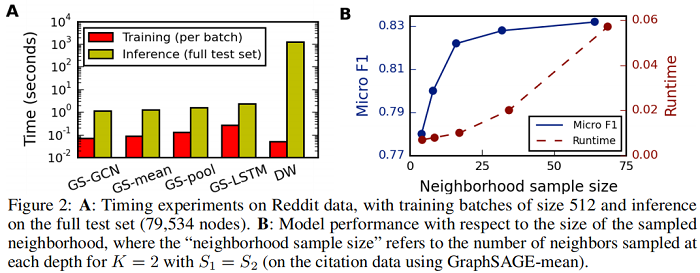
修改时间
2022-01-17 创建文章
2022-06-07 修改文中关于直推式和归纳式学习的定义
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15439876.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号