信息传递

有 n个同学（编号为 1 到 n）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 i 的同学的信息传递对象是编号为 Ti​ 的同学。 游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入格式

输入共 22 行。

第 1 行包含 1 个正整数 n，表示 n 个人。

第 2 行包含 n 个用空格隔开的正整数 T1​,T2​,…,Tn​，其中第 Ti个整数表示编号为 ii的同学的信息传递对象是编号为Ti​ 的同学，Ti​≤n 且Ti​!​=i。

数据保证游戏一定会结束。

输出格式

输出共 11 行，包含 11 个整数，表示游戏一共可以进行多少轮。

数据范围

对于 30% 的数据 n≤200；

对于 60% 的数据，n≤2500；

对于 100% 的数据，n≤200000。

样例说明

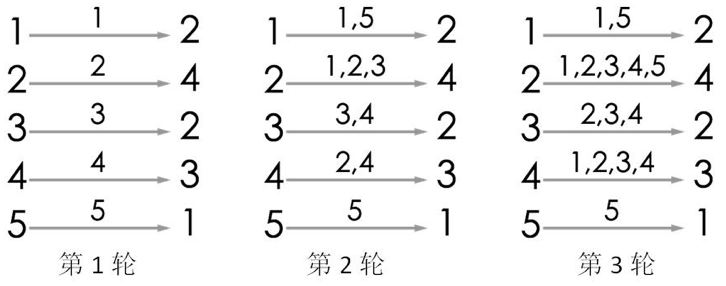
游戏的流程如图所示。当进行完第 3轮游戏后，4 号玩家会听到 2 号玩家告诉他自己的生日，所以答案为 3。当然，第 3 轮游戏后，22号玩家、3号玩家都能从自己的消息 来源得知自己的生日，同样符合游戏结束的条件。

输出时每行末尾的多余空格，不影响答案正确性

样例输入

5
2 4 2 3 1

样例输出

3

 

 

#include<cstdio>
#include<iostream>
using namespace std;
int f[200002],d[200002],n,minn,last;   //f保存祖先节点，d保存到其祖先节点的路径长。 
int fa(int x)
{
    if (f[x]!=x)                       //查找时沿途更新祖先节点和路径长。 
    {
        int last=f[x];                 //记录父节点（会在递归中被更新）。 
        f[x]=fa(f[x]);                 //更新祖先节点。 
        d[x]+=d[last];                 //更新路径长（原来连在父节点上）。 
    }
    return f[x];
}
void check(int a,int b)
{
    int x=fa(a),y=fa(b);               //查找祖先节点。 
    if (x!=y) {f[x]=y; d[a]=d[b]+1;}   //若不相连，则连接两点，更新父节点和路径长。 
    else minn=min(minn,d[a]+d[b]+1);   //若已连接，则更新最小环长度。 
    return;
}
int main()
{
    int i,t;
    cin>>n;
    for (i=1;i<=n;i++) f[i]=i;         //祖先节点初始化为自己，路径长为0。 
    minn=0x7777777;
    for (i=1;i<=n;i++)
    {
        cin>>t;
        check(i,t);                    //检查当前两点是否已有边相连接。 
    }
    cout<<minn<<endl;
    return 0;
}

 

 

 

#include<iostream>
using namespace std;
int dx[300000];//存每一个人传话的对象
bool visit[300000]={0},novisit[300000]={0};//visit存每次查找中被查到的点，而novisit存每次查找前，已经被查找过的点（及不用继续查找了）
int bs[300000]={0};//每次查找中第一次到一个节点所经过的边数
int minn=2e9;
void dfs(int node,int num)
{
    if(novisit[node])return;//不需要继续找了
    if(visit[node])//在此次查找中出现过
    {
        minn=min(minn,num-bs[node]);//形成一个环，取最小值
    }
    else
    {
        visit[node]=true;//在此次循环中经过
        bs[node]=num;//记录第一次到达时的步数
        dfs(dx[node],num+1);//搜索
        novisit[node]=true;//已经搜过
    }
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>dx[i];
    }
    for(int i=1;i<=n;i++)
    {
        dfs(i,0);//枚举全部节点
    }
    cout<<minn<<endl;//输出
    return 0;//时间复杂度O(n)
}