Blair

假设用一个 n×n 的数组 a来描述一个有向图的邻接矩阵：

（1）编写一个函数确定一个顶点的出度

（2）编写一个函数确定一个顶点的入度

（3）编写一个函数确定图中边的数目

输入格式

第一行：节点总数 n、指定节点 m。

下面n行：有向图的邻接矩阵

输出格式

第一行包括三个数据：节点编号 m、m 的出度、m 的入度（之间用一个空格隔开）。

第二行包括一个数据：图中边的总数。

数据范围

  1≤n,m,a[i][j]≤1000 。

输出时每行末尾的多余空格，不影响答案正确性

样例输入

5 3
0 4 2 2 3
2 0 1 5 10
2 0 0 4 0
0 3 7 0 7
6 2 0 0 0

样例输出

3 2 3
15

 

知识点补充：

下图中无向图G 5 和有向图G 6 的邻接矩阵分别为A1 和A 2 。

 

 

 

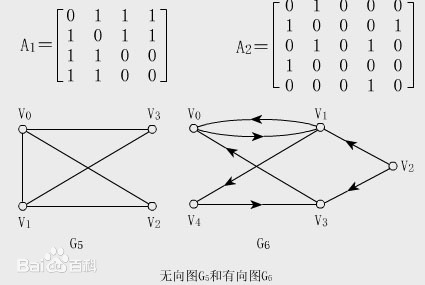
 带距离的邻接矩阵：

 

 

 

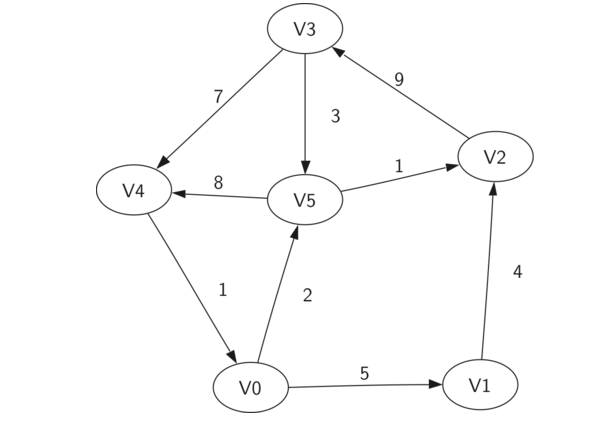
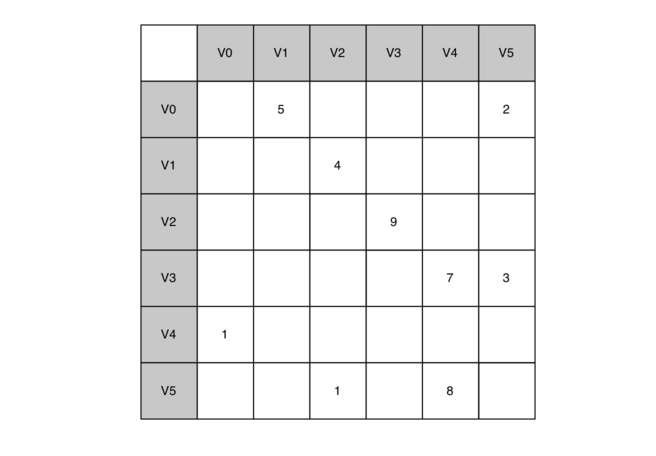
 代码：

#include<iostream>
using namespace std;
int main(){
    int n ,m;
    cin>>n>>m;
    int **arr =new int*[n];
    for (int i = 0; i < n; i++)
    {
        arr[i] = new int[n];
        for (int j = 0; j < n; j++)
        {
            cin>>arr[i][j];
        }
    }
    int chu=0,ru=0,total=0;
    for (size_t i = 0; i < n; i++)
    {
        if (arr[m-1][i]>0)
        {
           chu++;
        }
        if (arr[i][m-1]>0)
        {
            ru++;
        }
        for (int j = 0; j < n; j++)
        {
            if (arr[i][j]>0)
            {
                total++;
            }
        }
    }
    cout<<m<<" "<<chu<<" "<<ru<<endl;
    cout<<total<<endl;
}

 

 

#include<bits/stdc++.h>
#define MaxVertexNum 100 //最大顶点
#define INFINITY 65535 // ∞设为双字节无符号整数的最大值65535
using namespace std;

typedef int Vertex; //用顶点下标表示顶点,为整型
typedef int WeightType; //边的权值
typedef char DataType; //顶点储存的数据类型
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1,V2; //有向边<V1,V2>
    WeightType Weight; //权重
};
typedef PrtToENode Edge; //图结点的定义
typedef GNode *PtrToGNode;
struct GNode{
    int Nv; //顶点数
    int Ne; //边数
    WeightType G[MaxVertexNum][MaxVertexNum]; //邻接矩阵
    DataType Data[MaxVertexNum]; //存顶点的数据
    //注意：很多情况下，顶点无数据，此时Data[]可以不用出现
};
typedef PtrToGNode MGraph; //以邻接矩阵存储的图类型
MGraph CreatGraph(int VertexNum){
    /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V,W;
    MGraph Graph;
    Graph = (MGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;//初始化邻接矩阵，这里默认顶点编号从0开始，到(Graph->Nv-1)
    for(V = 0; V<Graph->Nv; V++){
        for(W = 0; W<Graph->Nv; W++){
            Graph->G[V][W] = INFINITY;
        }
    }
    return Graph;
}

void InsertEdge(MGraph Graph,Edge E){
    //插入边<V1,V2>
    Graph->G[E->V1][E->V2] = E->Weight; 
    //若是无向图，还要插入边<V1,V2>
    //Graph->G[E->V2][E->V1] = E->Weight;
}

MGraph BuildGraph(){
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv,i;
    scanf("%d",&Nv);//读入顶点个数
    Graph = CreatGraph(Nv);//初始化有nv个顶点但没有边的图
    scanf("%d",&(Graph->Ne));//边数
    if(Graph->Ne != 0){
        E = (Edge)malloc(sizeof(struct ENode));
        //建立边结点，读入边，格式化为“起点 终点 权重”，插入邻接矩阵
        for(i = 0; i<Graph->Ne; i++){
            scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
            //注意如果权重不是整型，%d要改
            InsertEdge(Graph , E);
        }
    }
    for(V = 0; V<Graph->Nv; V++){
        scanf("%c",&(Graph->Data[V]));
    }
    return Graph;
}