高级机器学习
人工智能学院
Homework 2
Instructor: 詹德川
Name: 胡涂, StudentId: 211820073
一、VC 维

Problem 1.1
令\(h_{x \in A}(x) = 1\),其他情况\(h(x) = -1\)
对于三点集,我们可以假设满足如下情况
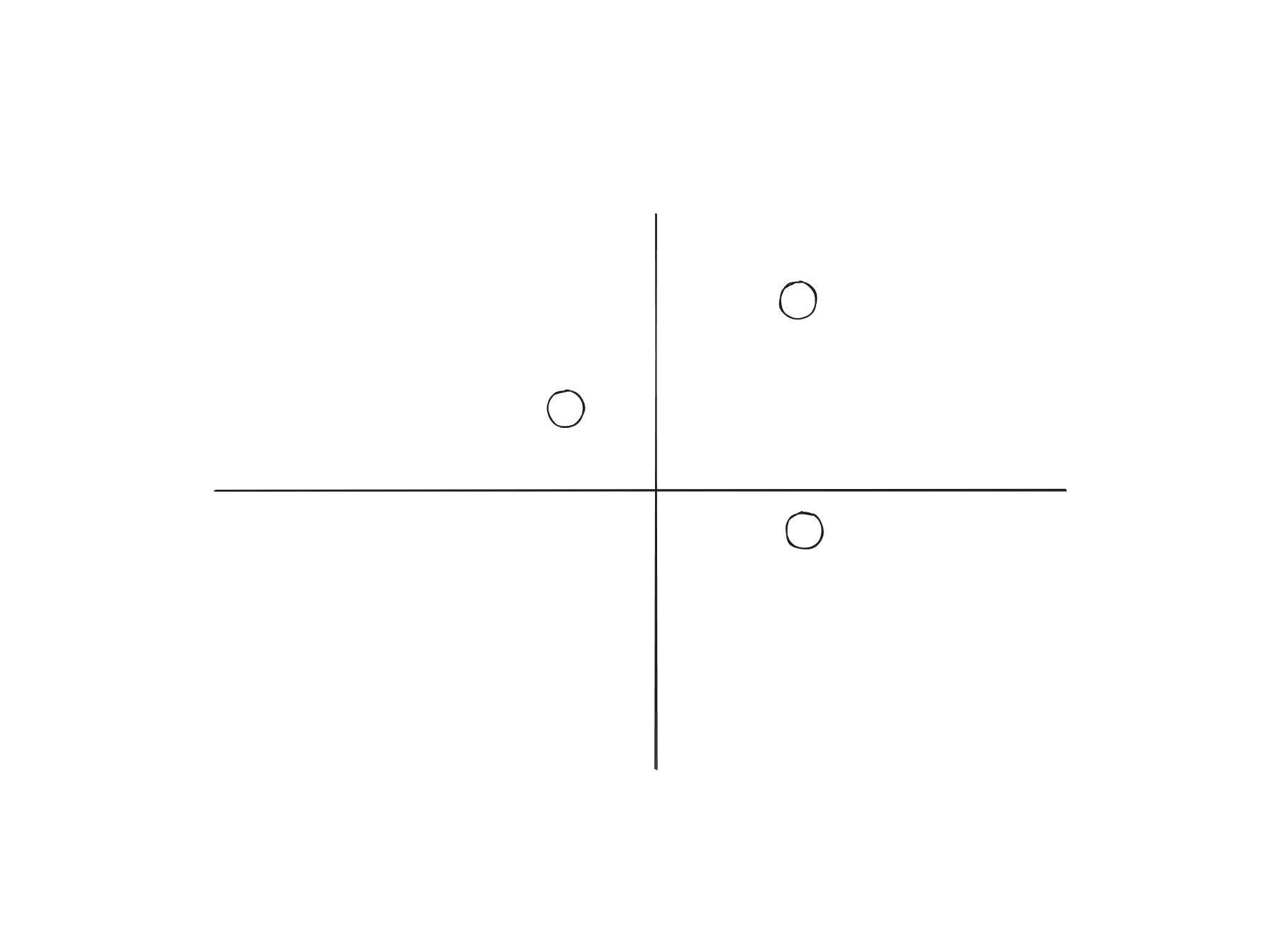
不难得出,所有的标记情况都能被实现对分,因此 VC 维至少为 3
如果我们选择 4 个点,它们构成一个凸四边形,那么无论我们如何画一个平行于坐标轴的矩形,这个矩形不能覆盖对角线上的两个点。
对于一个凹四边形,无论如何无法覆盖某一邻边上的两个点。
因此,VC 维为 3
Problem 1.2
考虑任意数量的点集,\((x_1, \dots, x_n)\),我们证明需要存在一个 1-近邻分类器,使得对于任意的标记集合\((y_1, \dots, y_n)\),都能被实现。
因此,只需要构造一个 1-近邻分类器,使得\(\forall x_i, \text{n}(x_i) \to y_i\)。
我们可以通过调整点的位置,使得每个点的最近邻就是它自己。这对于任意数量的点集都是成立的,所以对于任意数量的点集,我们都可以找到一个最近邻分类器使得其分类结果与预期一致。因此,最近邻分类器的假设空间可以对任意数量的点集进行打散。
所以,最近邻分类器的 VC 维为无穷大。
二、图半监督学习

上述正则化框架由两部分组成:
- 传播项:\(\sum_{i,j} W_{ij} || \frac{1}{\sqrt{d_i}}F_i - \frac{1}{\sqrt{d_j}}F_j||^2\), 这部分是为了保证相似的节点应当有同样的标签,\(W_{ij}\)是节点之间的相似度,而\(F\)是标记矩阵,通过最小化平方项保证相似的节点有相同的标签。
- 正则化项:\(\sum_{i=1}^l ||F_i - Y_i||^2\), 这部分是确保在标记传播的过程中,已知标签的节点尽量保持不变,能够保证在已知标签上的表现。
这个正则化框架通过两个项的平衡实现了对图中未标记节点标签的推断:传播项确保了标签信息能在图中相似的节点间有效传播,而拟合项则确保模型在已知标签节点上的预测准确性。
三、高斯混合模型

Problem 3.1
高斯混合模型:
\[p(x) = \sum_{k=1}^{K} p(z = k) \mathcal{N}(x | \mu_k, \Sigma_k)
\]
其中\(\mathcal{N}(x | \mu_k, \Sigma_k)\)由 k 唯一确定,因此可以用\(p(x|z)\)来表示,即为
\[p(x) = \sum_{k=1}^{K} p(z = k) p(x|z = k)
\]
\[p(x, z = (z_1, z_2, \dots, z_k)) = \prod_{i=1}^N p(x_i, z_i) = \prod_{i=1}^N p(z_i) p(x_i|z_i)
\]
使用概率图模型可以表示为:
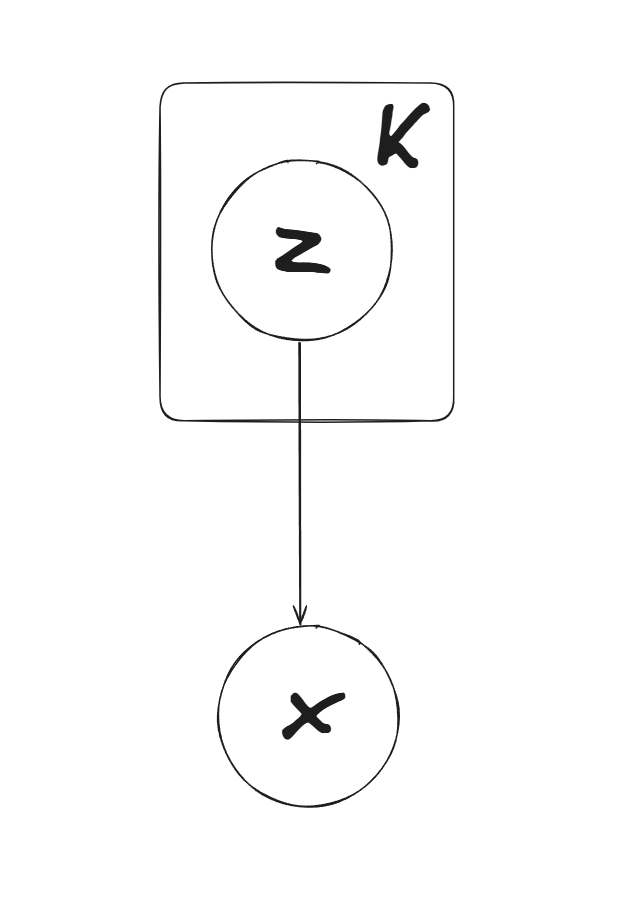
Problem 3.2
EM 算法的步骤为:
- E-step:求解\(\mathbb{E}_{p(z|x;\theta^t)}[\log p(x,z;\theta)]\)
- M-step:求解\(\theta^{t+1} = \arg \max_{\theta} \mathbb{E}_{p(z|x;\theta^t)}[\log p(x|z;\theta)]\)
我们假设样本集合为\(\{x_1, x_2, \cdots, x_N\}\),每一对\((x_i,z_i)\)相互独立
在 GMM 中,我们定义\(p(x,z;\theta)\)
\[p(x,z=(\dots);\theta) = \prod_{i=1}^N p(x_i,z_i;\theta_k) = \prod_{i=1}^N p(z_i) p(x_i|z_i) = \prod_{i=1}^N \pi_{z_i} \mathcal{N}(x_i|\mu_{z_i}, \Sigma)
\]
定义\(p(z|x;\theta)\)
\[p(z|x; \theta) = \prod_{i=1}^N p(z_i|x_i;\theta)
\]
\[p(z_i|x_i;\theta) = \frac{p(x_i|z_i)p(z_i)}{\sum_{k=1}^K p(x_i|z_i=k)p(z_i=k)}
\]
E-step:
\[\mathbb{E}_{p(z|x;\theta^t)}[\log p(x,z;\theta)] =
\sum_{k} p(z=k|x;\theta^t) \log p(x,z=k;\theta) = \\
\sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K \prod_{i=1}^N p(z_i|x_i;\theta^t) (\log \prod_{i=1}^N \pi_{z_i} \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K \prod_{i=1}^N p(z_i|x_i;\theta^t) \sum_{i=1}^N (\log \pi_{z_i} + \log \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{i=1}^N \sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K \prod_{i=1}^N p(z_i|x_i;\theta^t)(\log \pi_{z_i} + \log \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{i=1}^N \sum_{k = 1}^K p(z_i=k|x_i;\theta^t)(\log \pi_{k} + \log \mathcal{N}(x_i|\mu_{k}, \Sigma))
\]
M-step:
\[(\pi^{t+1}, \mu^{t+1}, \Sigma^{t+1}) = \\ \arg \max_{\pi, \mu, \Sigma} \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t)(\log \pi_{k} + \log \mathcal{N}(x_i|\mu_{k}, \Sigma)) \iff \\
\arg \max_{\pi, \mu, \Sigma} \sum_{i=1}^N \sum_{k = 1}^K p(z_i=k|x_i;\theta^t)\log \pi_{k} + \sum_{i=1}^N \sum_{k = 1}^K p(z_i=k|x_i;\theta^t) \log \mathcal{N}(x_i|\mu_{k}, \Sigma)
\]
那么,对于\(\pi^{t+1}\),
\[\pi^{t+1} = \arg \max_{\pi} \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t)\log \pi_{k}
\]
由于\(\sum_{k=1}^K \pi_k = 1\),可以使用拉格朗日乘子法求解,即
\[\mathcal{L}(\pi, \lambda) = \sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t) \log \pi_k + \lambda(1 - \sum_{k=1}^K \pi_k)
\]
对\(\pi_k\)求导,令导数为 0,即
\[\frac{\partial \mathcal{L}(\pi, \lambda)}{\partial \pi_k} =
\sum_{i=1}^N p(z=k|x_i;\theta^t) \frac{1}{\pi_k} - \lambda = 0
\Rightarrow \pi_k^{t+1} = \frac{\sum_{i=1}^N p(z=k|x_i;\theta^t)}{\lambda} = \\
\frac{\sum_{i=1}^N p(z=k|x_i;\theta^t)}{\sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t)} = \frac{\sum_{i=1}^N p(z=k|x_i;\theta^t)}{N}
\]
其中\(\lambda\)由\(\sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t) = N\)确定
对于\(\mu^{t+1}\),
\[\mu^{t+1} = \arg \max_{\mu} \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t) \log \mathcal{N}(x_i|\mu_{k}, \Sigma)
\]
由于\(\mu\)各分量之间无关,因此可以分别求解
\[\mu_k^{t+1} = \arg \max_{\mu_k} \sum_{i=1}^N p(z=k|x_i;\theta^t) \log \mathcal{N}(x_i|\mu_{k}, \Sigma) = \\
\argmax_{\mu_k} \sum_{i=1}^N p(z=k|x_i;\theta^t) \left( -\frac{d}{2} \log 2\pi - \frac{1}{2} \log |\Sigma| - \frac{1}{2}(x_i - \mu_k)^T \Sigma^{-1} (x_i - \mu_k) \right)
\]
对\(\mu_k\)求导,令导数为 0,即
\[\frac{\partial}{\partial \mu_k} \sum_{i=1}^N p(z=k|x_i;\theta^t) \left( -\frac{d}{2} \log 2\pi - \frac{1}{2} \log |\Sigma| - \frac{1}{2}(x_i - \mu_k)^T \Sigma^{-1} (x_i - \mu_k) \right) = 0 \Rightarrow \\
\sum_{i=1}^N p(z=k|x_i;\theta^t) \Sigma^{-1} (x_i - \mu_k) = 0 \Rightarrow \\
\mu_k^{t+1} = \frac{\sum_{i=1}^N p(z=k|x_i;\theta^t) x_i}{\sum_{i=1}^N p(z=k|x_i;\theta^t)}
\]
对于\(\Sigma^{t+1}\),
\[\Sigma^{t+1} = \arg \max_{\Sigma} \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t) \log \mathcal{N}(x_i|\mu_{k}, \Sigma)
\]
对\(\Sigma\)求导,令导数为 0,即
\[\frac{\partial}{\partial \Sigma} \sum_{i=1}^N \sum_{k=1}^K p(z=k|x_i;\theta^t) \left( -\frac{d}{2} \log 2\pi - \frac{1}{2} \log |\Sigma| - \frac{1}{2}(x_i - \mu_k)^T \Sigma^{-1} (x_i - \mu_k) \right) = 0 \\
\Rightarrow \sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t) \left( -\frac{1}{2} \Sigma^{-1} + \frac{1}{2} \Sigma^{-1} (x_i - \mu_k) (x_i - \mu_k)^T \Sigma^{-1} \right) = 0 \\
\Rightarrow \Sigma^{t+1} = \frac{\sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t) (x_i - \mu_k) (x_i - \mu_k)^T}{\sum_{k=1}^K \sum_{i=1}^N p(z=k|x_i;\theta^t)}
\]







 浙公网安备 33010602011771号
浙公网安备 33010602011771号