数据结构 - 树 - 二叉树基本介绍
二叉树定义
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根结点加上两棵分别称为左子树和右子树的,互不相交的二叉树构成。
形式定义
对数据元素集合 \(D\),其上的数据关系 \(R\) 满足:
-
若 \(D=\empty\),则 \(R=\empty\),称为空二叉树。
-
若 \(D\neq \empty\),则 \(R=\{H\}\),\(H\) 是如下二元关系:
-
在 \(D\) 中存在唯一的称为根的数据元素 \(\text{root}\),它在关系 \(H\) 下无前驱。
-
若 \(D-\{\text{root}\}\neq \empty\),则存在 \(D-\{\text{root}\}=\{D_l,D_r\}\),且 \(D_l \cap D_r = \empty\)。
二叉树的五种基本形态
根据上述的二叉树定义,我们可以得到二叉树的五种基本形态:
说明:
-
二叉树中每个结点最多有两棵子树;二叉树每个结点度小于等于 \(2\);
-
左、右子树不能颠倒,即二叉树是一棵有序树。
两类特殊的二叉树
满二叉树:指的是深度为 \(k\) 且含有 \(2^k - 1\) 个结点的二叉树。
完全二叉树:树中所含的 \(n\) 个结点和满二叉树中编号为 \(1\) 至 \(n\) 的结点一一对应。
下图中,左图展示了满二叉树,右图展示了一个对应的完全二叉树。
二叉树的性质
性质 1
在二叉树的第 \(i\) 层上至多有 \(2^{i-1}\) 个结点(\(i \geqslant 1\))。
证明:用数学归纳法证明,当 \(i=1\) 层时,只有一个根结点,此时满足
假设对所有 \(j \, (1 \leqslant j < i)\),命题成立。则根据假设,第 \(i-1\) 层至多有 \(2^{i-2}\) 个结点,由于二叉树上每个结点至多有两棵子树,则第 \(i\) 层结点数至多有
证毕。
性质 2
深度为 \(k\,(k \geqslant 1)\) 的二叉树上至多含 \(2^{k}-1\) 个结点。
证明:基于性质 1,我们可知深度为 \(k\,(k \geqslant 1)\) 的二叉树上结点数至多为
证毕。
可有性质 2 得到如下推论。
推论
具有 \(n \, (n \geqslant 1)\) 个结点的二叉树,高 \(h\) 至少是 \(\lfloor \log_2 n \rfloor + 1\)。
证明:设 高为 \(h\),则该树满足条件
故高 \(h\) 至少是 \(\lfloor \log_2 n \rfloor + 1\)。
证毕。
性质 3
对任何一棵非空二叉树,若它含有 \(n_0\) 个叶子结点(结点度为零的结点)、\(n_2\) 个结点度为 \(2\) 的结点,则必存在关系式:
\[n_0 = n_2 + 1 \]
证明:设二叉树上的结点总数
又二叉树上的分支总数 \(b\) 等于从结点出发的边
而除根结点外 \(n\) 个点需要 \(n-1\) 条边连接,故有
由此得到 \(n_0 = n_2 + 1\)。
证毕。
性质 4
具有 \(n \, (n \geqslant 1)\) 个结点的完全二叉树的深度为 \(\lfloor \log_2 n\rfloor + 1\)。
证明:设完全二叉树的深度为 \(k\),则根据性质 \(2\) 得到
由于 \(n\) 为正整数,故有
又由于 \(k\) 只能为整数,故有
证毕。
性质 5
若对含 \(n\) 个结点的完全二叉树从上到下且从左至右进行 \(1\) 到 \(n\) 的编号,则对完全二叉树中任意一个编号为 \(i\) 的结点:
若 \(i=1\),则该结点是二叉树的根,无双亲;否则 \(i \neq 1\),编号为 \(\lfloor i/ 2\rfloor\) 的结点为其双亲结点。
若 \(2i > n\),则该结点无左孩子结点;否则,编号为 \(2i\) 的结点为其左孩子结点。
若 \(2i + 1 > n\),则该结点无右孩子结点;否则,编号为 \(2i+1\) 的结点为其右孩子结点。
该性质也可用图表示如下:
证明:在此过程中,我们可以由第二点和第三点推出第一点。所以我们先证明第二点和第三点。
对于 \(i=1\),由完全二叉树的定义,其左孩子是结点 \(2\),若 \(2>n\),即不存在结点 \(2\)。此时,结点 \(i\) 无孩子。类似地,结点 \(i\) 的右孩子也只能是结点 \(3\),若 \(3>n\),显然此时结点 \(i\) 无右孩子。
对于 \(i > 1\),可分为两种情况:
(1)设第 \(j \, (1 \leqslant j \leqslant \lfloor \log_2 n\rfloor)\) 层的第一个结点的编号为 \(i\),由二叉树的性质 \(2\) 和定义可知 \(i=2^{j-1}\)。结点 \(i\) 的左孩子必定为第 \(j+1\) 层的第一个结点,其编号为 \(2^j=2 \cdot 2^{j-1}=2i\)。如果 \(2^i > n\),则无左孩子;其右孩子必定为第 \(j+1\) 层的第二个结点,编号为 \(2i+1\)。若 \(2i+1 > n\),则无右孩子。
(2)假设第 \(j \, (1 \leqslant j \leqslant \lceil \log_2 n\rceil)\) 层上的某个结点编号为 \(i\),且 \(2i+1<n\),其左孩子为 \(2 i\),右孩子为 \(2i+1\),则编号为 \(i+1\) 的结点是编号为 \(i\) 的结点的右兄弟或堂兄弟。若它有左孩子,则其编号必定为 \(2i+2=2\times (i+1)\),若它有右孩子,则其编号必定为 \(2i+3=2\times (i+1)+1\)。
当 \(i=1\) 时,就是根,因此无双亲,当 \(i>1\) 时,如果 \(i\) 为左孩子,即 \(2 \times (i / 2)=i\),则 \(i/2\) 是 \(i\) 是双亲;如果 \(i\) 为右孩子,则有 \(i=2p+1\),\(i\) 是双亲为 \(p\),而此时 \(p = \lfloor i/2\rfloor\)。
证毕。
二叉树的存储结构
二叉树的顺序结构表示
对于完全二叉树,可以采用一组连续的内存单元,按编号顺序依次存储完全二叉树的结点。
对于一棵一般的二叉树,如果补齐构成完全二叉树所缺少的那些结点,便可以对二叉树的结点进行编号。
对于一些“退化二叉树”,顺序存储结构存在突出缺点:比较浪费空间。
二叉树的二叉链表表示
二叉链表中每个结点包含三个域:数据域、左指针域、右指针域。
typedef struct BiTNode
{
ElemType data; // 数据域
struct BiTNode* lchild, * rchild; // 左指针域、右指针域
} BiTNode, * BiTree;
下图展示了一棵二叉树的二叉链表表示。
考虑一棵有 \(n\) 个结点的二叉树,我们容易证明该二叉树的二叉链表表示中共有 \(n+1\) 个空指针(对结点数 \(n\) 做数学归纳法)。
二叉树的三叉链表表示
三叉链表中每个结点包含四个域:数据域、双亲指针域、左指针域、右指针域。
typedef struct BiTNode
{
ElemType data; // 数据域
struct BiTNode* lchild, * rchild; // 左指针域、右指针域
struct BiTNode* parent; // 双亲指针域
} BiTNode, * BiTree;
下面给出一棵二叉树的三叉链表表示中的结点结构图示:
下图展示了一棵二叉树的三叉链表表示。
静态二叉链表表示
我们可以采用一个数组来存储类似于二叉链表表示中的结点。下图展示了一棵二叉树的静态二叉链表表示。
此时一般使用类似下面的代码,通过静态二叉链表来定义一棵二叉树。
typedef struct BPTNode { // 结点结构
TElemType data;
int lchild, rchild;
} BNode;
typedef struct BTree { // 树结构
BNode nodes[MAX_TREE_SIZE];
int num_node; // 结点数目
int root; // 根结点的位置
} BTree;
双亲链表
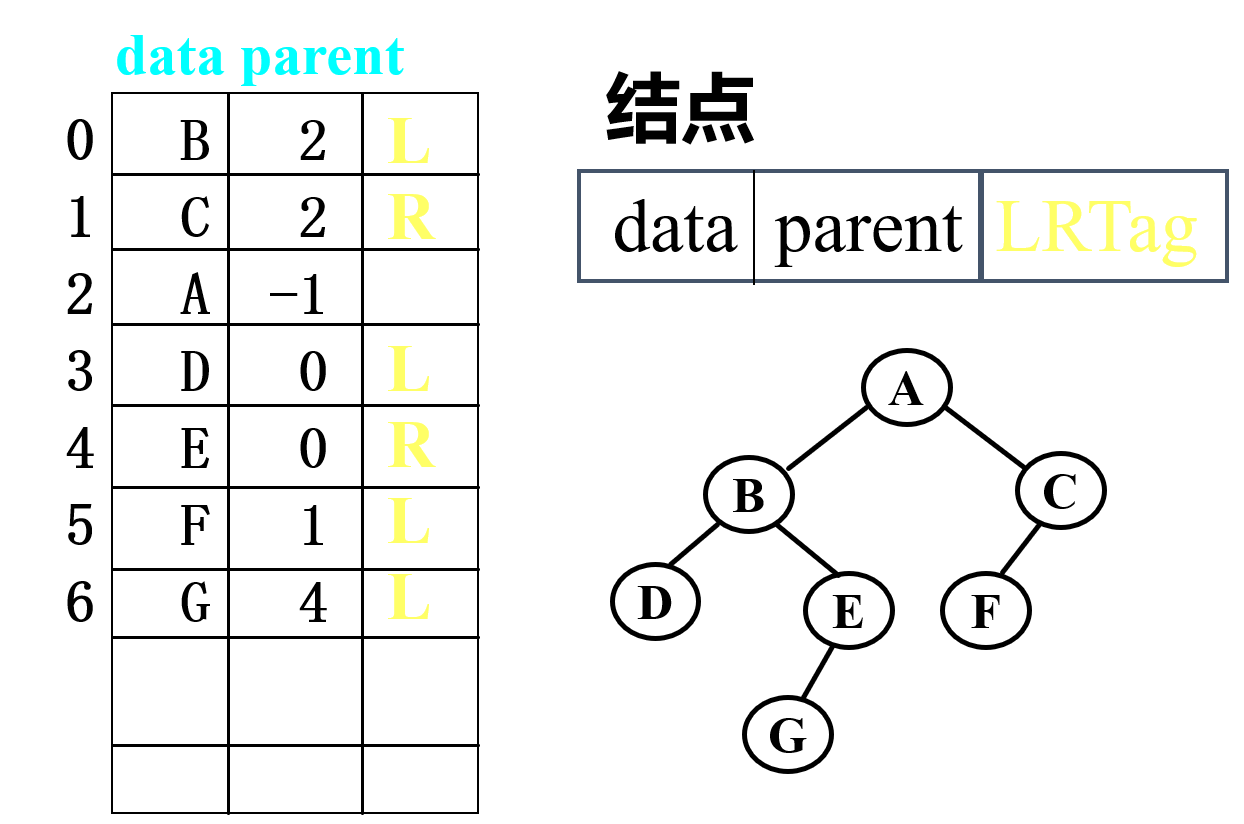
typedef struct BPTNode { // 结点结构
TElemType data;
int parent; // 指向双亲的指针
char LRTag; // 左、右孩子标志域
} BPTNode;
typedef struct BPTree { // 树结构
BPTNode nodes[MAX_TREE_SIZE];
int num_node; // 结点数目
int root; // 根结点的位置
} BPTree;
二叉树的创建
二叉树的遍历
遍历的基本概念
-
遍历:按某种搜索策略(路径)访问树或图中的每个结点,且每个结点仅被访问一次。
-
访问:含义很广,可以解释为对结点的各种处理,如修改结点的数据,输出结点数据等。
遍历是各种数据结构最基本的操作,许多其他的操作可以在遍历基础上实现。
遍历对线性结构很容易,但二叉树每个结点都可能有两棵子树,我们可以通过寻找一种规律,使二叉树中的结点能线性排列。
遍历二叉树
按某种次序依次访问二叉树中的结点,要求每个结点访问一次且仅访问一次。
线性结构只有一条访问路径,二叉树是非线性结构,需要确定访问的顺序。
我们令:
-
L:遍历左子树。
-
D:访问根结点。
-
R:遍历右子树。
此时我们可知,共有六种基本的遍历方法。
基本:DLR,LDR,LRD
镜像:DRL,RDL,RLD
如果我们约定先左后右,则有三种遍历方法:DLR,LDR,LRD。分别根据访问根结点的次序称为:先序遍历、中序遍历、后序遍历。
先序遍历(DLR)
若二叉树非空,我们按下述顺序遍历二叉树。
-
(1)访问根结点;
-
(2)遍历左子树;
-
(3)遍历右子树。
对一棵二叉树进行先序遍历的递归算法可用如下代码表示:
void PreOrderTraverse(BiTree T, Status(*Visit) (ElemType e))
{
// 采用二叉链表存贮二叉树,visit( )是访问结点的函数
// 本算法先序遍历以T为根结点指针的二叉树
if (T) { // 若二叉树不为空
Visit(T->data); // 访问根结点
PreOrderTraverse(T->lchild, Visit); // 先序遍历T的左子树
PreOrderTraverse(T->rchild, Visit); // 先序遍历T的右子树
}
} // PreOrderTraverse
// 最简单的 visit 函数是:
Status PrintElement(ElemType e)
{ //输出元素e的值
output(e);
return OK;
}
有另一种利用了 visit 函数信息的先序遍历的递归算法:
Status PreOrderTraverse(BiTree T, Status(*Visit) (ElemType e))
{
// 采用二叉链表存贮二叉树, visit( )是访问结点的函数
if (T) {
if (Visit(T->data)) { // 如果访问根结点成功,则继续
if (PreOrderTraverse(T->lchild, Visit)) //左子树
if (PreOrderTraverse(T->rchild, Visit)) //右子树
return OK;
}
return ERROR;
}
else return OK;
} // PreOrderTraverse
中序遍历(LDR)
若二叉树非空,我们按下述顺序遍历二叉树。
-
(1)遍历左子树;
-
(2)访问根结点;
-
(3)遍历右子树。
对一棵二叉树进行中序遍历的递归算法可用如下代码表示:
Status InOrderTraverse(BiTree T, Status(*Visit) (ElemType e))
{
// 采用二叉链表存贮二叉树, visit( )是访问结点的函数
// 本算法中序遍历以T为根结点指针的二叉树
if (T) { // 若二叉树不为空
InOrderTraverse( T->lchild, Visit ); // 中序遍历T的左子树
Visit(T->data); // 访问根结点
InOrderTraverse( T->rchild, Visit ); // 中序遍历T的右子树
}
return OK;
} // InOrderTraverse
后序遍历(LRD)
若二叉树非空,我们按下述顺序遍历二叉树。
-
(1)遍历左子树;
-
(2)遍历右子树;
-
(3)访问根结点。
对一棵二叉树进行后序遍历的递归算法可用如下代码表示:
void PostOrderTraverse(BiTree T, Status (*Visit) (ElemType e))
{
// 采用二叉链表存贮二叉树, visit( )是访问结点的函数
// 本算法后序遍历以T为根结点指针的二叉树
if (T) { // 若二叉树不为空
PostOrderTraverse(T->lchild, Visit); // 后序遍历左子树
PostOrderTraverse(T->rchild, Visit); // 后序遍历右子树
Visit(T->data); // 访问根结点
}
} // PostOrderTraverse
二叉树遍历的一些实际例子
例 1
编写求二叉树的叶子结点个数的算法。该算法输入为一棵二叉树的二叉链表,输出为该二叉树的叶子结点个数。
void leaf(BiTree T)
{
// 二叉链表存贮二叉树,计算二叉树的叶子结点个数
// 先序遍历的过程中进行统计,初始全局变量 n = 0
if (T) {
if (T->lchild == NULL && T->rchild == NULL) {
n += 1; // 若T所指结点为叶子结点则计数
} else {
leaf(T->lchild);
leaf(T->rchild);
}
} // if
} // leaf
有另一种不使用全局变量的方法。
int Countleave(BiTree T)
{
// 采用二叉链表存贮二叉树,返回叶子结点的个数
if (!T) return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1;
else
return Countleave(T->lchild) + Countleave(T->rchild);
}
例 2
是否可利用“遍历”,建立二叉链表的所有结点并完成相应结点的链接?即用二叉链表表示来建立一棵二叉树。
输入(在空子树处添加字符 \(*\) 的二叉树的)先序序列(不妨设每一个结点元素是一个字符)。按先序遍历的顺序,建立二叉链表的所有结点并完成相应结点的链接。
对原来的二叉树进行扩充,在空子树处添加 \(*\)。
void CreateBiTree(BiTree& T, char*& str) {
if (*str == '*') { T = NULL; str++;}
else {
if (!(T = (BiTNode*)malloc(sizeof(BiTNode))))
exit(OVERFLOW);
T->data = *str++; // 生成根结点(基本操作)
CreateBiTree(T->lchild, str); // 构造左子树
CreateBiTree(T->rchild, str); // 构造右子树
} // if (*str==' ') … else
} // CreateBiTree
例 3
复制二叉链表。该算法输入为一棵二叉树的二叉链表,输出为复制的新二叉链表。
void CopyBiTree(BiTree T, BiTree& newT)
{
// 采用后序遍历,新二叉链表根为 newT
if (!T) newT = NULL;
else
{
CopyBiTree(T->lchild, plchild); // 复制左子树
CopyBiTree(T->rchild, prchild); // 复制右子树
newT = (BiTree)malloc(sizeof(BiTNode));
newT->data = T->data; // 复制当前结点
newT->lchild = plchild; // 链接新结点的左子树
newT->rchild = prchild; // 链接新结点的右子树
}
}
例 4
求二叉树的深度。若一棵二叉树为空,则它的深度为 \(0\),否则它的深度等于其左右子树中的最大深度加 \(1\)。
int BinTreeDepth(BiTree bt) // 求二叉树的深度
{
if (bt == NULL)
return 0; // 对于空树,返回0值
else
{
depl = BinTreeDepth(bt->lchild); // 求左子树深度
depr = BinTreeDepth(bt->rchild); // 求右子树深度
if (depl > depr)
return depl + 1;
else
return depr + 1;
}
}
线索二叉树
通过遍历二叉树,我们可以得到结点的一个线性序列。
我们希望不必每次都通过遍历找出这样的线性序列。只要事先做预处理,将某种遍历顺序下的前驱、后继关系记在树的存储结构中,以后就可以高效地找出某结点的前驱、后继。
如何在二叉链表中保存线索?我们可以借用结点的空链域保存线索。指向线性序列中的“前驱”和“后继”的指针,称作“线索”。
包含“线索”的存储结构,称作“线索链表”。
线索链表中的结点
我们可以在二叉链表的结点中增加两个标志域 Ltag 和 Rtag。两个标志域取值为 \(0\) 或 \(1\)。
-
\(0\) 表示
lchild为指向左孩子的指针。 -
\(1\) 表示
lchild为指向直接前驱的线索。 -
\(0\) 表示
rchild为指向右孩子的指针。 -
\(1\) 表示
rchild为指向直接后继的线索。
下面给出线索链表的类型说明:
typedef enum { link, thread } PointerTag;
// link=0, thread=1
typedef struct BiThrNode {
ElemType data;
struct BiThrNode* lchild, * rchild;
PointerTag Ltag, Rtag; //左、右标志域
} BiThrNode, * BiThrTree;
线索二叉树的遍历
以中序线索二叉树为例。
-
中序遍历的第一个结点:二叉树的最左下结点。
-
当前结点的后继结点:若结点的右链域为线索,则后继结点为右链结点;否则,后继结点为右子树的最左下结点。
Status InTra_ThrT(BiThrTree ThrT, void (*Visit) (TElemType e))
{
BiThrNode* p = ThrT->lchild; // ThrT指向根结点
while (p != ThrT)
{
while (p->Ltag == link) p = p->lchild; // 最左下结点
Visit(p->data); // p->Ltag== thread
while (p->Rtag == Thread && p->rchild != ThrT)
{
// 若右孩子域是线索
p = p->rchild;
Visit(p->data);
}
p = p->rchild; // 若右孩子域不是线索
}
return OK;
} // InTra_ThrT
二叉树的线索化
在中序遍历过程中为二叉树的结点添加线索。
在添加线索的过程中,我们增加指针 pre 和 p,并保持指针 p 指向当前访问的结点,pre 指向当前访问结点的前驱。
void InThreading(BiThrTree p) // 中序线索化二叉树
{ // pre为全局变量,初值为NULL
if (p) {
InThreading(p->lchild); // 左子树线索化
if (p->lchild == NULL) { // 为当前结点加前趋线索
p->Ltag = Thread; p->lchild = pre;
}
if (pre->rchild == NULL) { // 为前趋结点加后继线索
pre->Rtag = Thread; pre->rchild = p;
}
pre = p; // pre指向p
InThreading(p->rchild);
} // if
} // InThreading
Status InThread(BiThrTree& Thrt, BiThrTree T)
{
if (Thrt = (BiThrTree)malloc(sizeof(BiThrNode))) {
exit(OVERFLOW);
}
Thrt->Ltag = Link; // 0
Thrt->Rtag = Thread; // 1. 建头结点
Thrt->rchild = Thrt; // 右指针指向头结点
if (!T)
Thrt->lchild = Thrt; // 左指针指向头结点
else {
Thrt->lchild = T; // 树非空,左指针指向根结点
pre = Thrt; // 头结点是中序第一个结点的前趋
InThreading(T); // 中序线索化
pre->rchild = Thrt; // 最后一个结点线索化
pre->Rtag = Thread;
Thrt->rchild = pre;
} // 进行中序线索化
return OK;
} // InThread






















 浙公网安备 33010602011771号
浙公网安备 33010602011771号