队列 and 环形队列(Queue)-Java版

队列简介

　　队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

　　队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。 

 

顺序队列实现

　　由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素，如图 1 所示：

　　

 

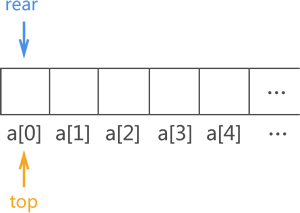
　　由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

　　在图 1 的基础上，当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

例如，在图 1 基础上将 {1,2,3,4} 用顺序队列存储的实现操作如图 2 所示：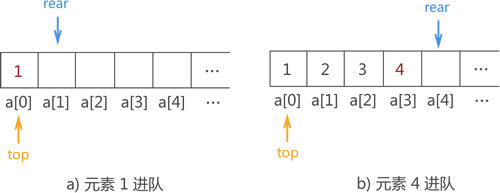

 

 

 

 

 

 

 

在图 2 基础上，顺序队列中数据出队列的实现过程如图 3 所示：

 

 

代码实例

package queue;

/**
 * ArrayQueue[数组队列实现]
 *
 */

class ArrayQueue {
    private int maxSize;
    private int front;
    private int rear;
    private int[] arr;

    public ArrayQueue(int maxSize) {
        this.maxSize = maxSize;
        front = -1;
        rear = -1;
        arr = new int[this.maxSize];
    }

    /**
     * 判断队列是否满了
     *
     * @return
     */
    public boolean isFull() {
        return rear == maxSize - 1;
    }

    /**
     * 判断队列是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return front == rear;
    }

    /**
     * 入队
     * @param element
     */
    public void addQueue(int element) {
        if (isFull()) {
            System.out.println("队列元素已满");
            return;
        }
        arr[++rear] = element;
    }

    /**
     * 出队
     * @return
     */
    public int getQueue() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        return arr[++front];
    }

    /**
     * 遍历队列
     */
    public void list() {
        if (isEmpty()) {
            System.out.println("队列为空");
        }
        for (int i = front + 1; i <= rear; i++) {
            System.out.printf("arr[%d] = %d\n", i, arr[i]);
        }
    }

    /**
     * 返回队列头元素
     * @return
     */
    public int headQueue() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        return arr[front + 1];
    }

}

public class ArrayQueueDemo {
    public static void main(String[] args) {
        ArrayQueue aq = new ArrayQueue(5);
    }
}

 

此方法存在的问题

　　先来分析以下图 2b) 和图 3b)。图 2b) 是所有数据进队成功的示意图，而图 3b) 是所有数据全部出队后的示意图。通过对比两张图，你会发现，指针 top 和 rear 重合位置指向了  a[4] 而不再是 a[0]。也就是说，整个顺序队列在数据不断地进队出队过程中，在顺序表中的位置不断后移。

顺序队列整体后移造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
• 如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；

为了避免以上两点，我建议初学者使用下面的方法实现顺序队列。

顺序队列另一种实现方法

既然明白了上面这种方法的弊端，那么我们可以试着在它的基础上对其改良。

为了解决以上两个问题，可以使用巧妙的方法将顺序表打造成一个环状表，如图 4 所示：

 

 

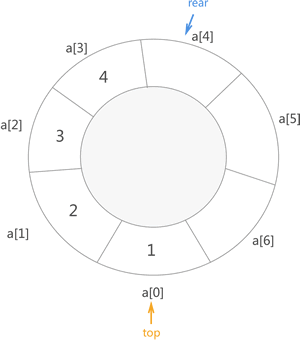
图 4 只是一个想象图，在真正的实现时，没必要真创建这样一种结构，我们还是使用之前的顺序表，也还是使用之前的程序，只需要对其进行一点小小的改变：

package queue;

/**
 * CircleArrayQueue(环形队列)
 *    
*/
class CircleArrayQueue {
    private int maxSize;
    private int front;
    private int rear;
    private int[] arr;

    public CircleArrayQueue(int arrMaxSize) {
        maxSize = arrMaxSize;
        arr = new int[maxSize];
    }

    // 判断队列是否满
    public boolean isFull() {
        return (rear + 1) % maxSize == front;
    }

    // 判断队列是否为空
    public boolean isEmpty() {
        return rear == front;
    }

    public void addQueue(int element) {
        if (isFull()) {
            System.out.println("队列满，不能加入数据~");
            return;
        }
        arr[rear] = element;
        rear = (rear + 1) % maxSize;
    }

    public int getQueue() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        int value = arr[front];
        front = (front + 1) % maxSize;
        return value;

    }

    public void showQueue() {
        if (isEmpty()) {
            System.out.println("队列为空");
            return;
        }
        for (int i = front; i < front + size(); i++) {
            System.out.printf("arr[%d]=%d\n", i % maxSize, arr[i % maxSize]);
        }
    }

    public int size() {
        return (rear + maxSize - front) % maxSize;
    }

    public int headQueue() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        return arr[front];
    }
}

public class CircleArrayQueueDemo {
    public static void main(String[] args) {

    }
}