bzoj1485--HNOI2009有趣的数列--Catalan数
Description
我们称一个长度为2n的数列是有趣的,当且仅当该数列满足以下三个条件:
(1)它是从1到2n共2n个整数的一个排列{ai};
(2)所有的奇数项满足a1<a3<…<a2n-1,所有的偶数项满足a2<a4<…<a2n;
(3)任意相邻的两项a2i-1与a2i(1≤i≤n)满足奇数项小于偶数项,即:a2i-1<a2i。
现在的任务是:对于给定的n,请求出有多少个不同的长度为2n的有趣的数列。因为最后的答案可能很大,所以只要求输出答案 mod P的值。
Input
输入文件只包含用空格隔开的两个整数n和P。输入数据保证,50%的数据满足n≤1000,100%的数据满足n≤1000000且P≤1000000000。
Output
仅含一个整数,表示不同的长度为2n的有趣的数列个数mod P的值。
Sample Input
3 10
Sample Output
5
对应的5个有趣的数列分别为(1,2,3,4,5,6),(1,2,3,5,4,6),(1,3,2,4,5,6),(1,3,2,5,4,6),(1,4,2,5,3,6)。
对应的5个有趣的数列分别为(1,2,3,4,5,6),(1,2,3,5,4,6),(1,3,2,4,5,6),(1,3,2,5,4,6),(1,4,2,5,3,6)。
题解:
打表可以看出来,这题的结果是求卡特兰数第n项……
当然也可以有实际意义,其中奇数项为入栈,偶数项为出栈,用1~2N这些数放进去,就成了卡特兰数。
卡特兰数的公式 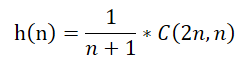
将式子展开以后得到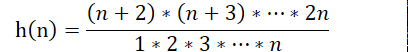
 View Code
View Code
因为数据范围很大,且p不保证是质数。我们考虑用分解质因数的方法来表示h(n),因为n+2~2n是在分子上,所以指数为正,而1~n在分母上,所以指数为负。
对于数字i,当我们要把它的k次方放进结果中时,如果a是i的质因数,就把a的指数和i/a的指数都加k。
因为上述过程可以迭代进行,故我们只需要求出数字的最小质因数即可,用线性筛求出。
最后用一下快速幂将每个数字与其指数的结果乘到ans中。

1 #include<iostream> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstdio> 5 #include<cstring> 6 #define ll long long 7 using namespace std; 8 9 const int maxn=2000009;//mindiv是最小质因数 10 int n,p,mindiv[maxn],pri[maxn],cnt[maxn],tot=0; 11 //cnt数组记录指数的值 12 ll poww(ll x,ll y,ll m) 13 {//快速幂 14 ll ret=1; 15 while(y) 16 { 17 if(y&1) 18 ret=1ll*ret*x%m; 19 x=1ll*x*x%m; 20 y>>=1; 21 } 22 return ret; 23 } 24 25 void getpri(int n) 26 {//线性筛 27 for(int i=2;i<=n;i++) 28 { 29 if(!mindiv[i]) 30 pri[++tot]=mindiv[i]=i; 31 for(int j=1,k;j<=tot&&pri[j]<=mindiv[i]&&(k=pri[j]*i)<=n;j++) 32 { 33 mindiv[k]=pri[j]; 34 if(i%pri[j]==0)break; 35 } 36 } 37 } 38 39 void calc(int x,int y) 40 {//计算指数 41 while(x>1) 42 { 43 cnt[mindiv[x]]+=y; 44 x/=mindiv[x]; 45 } 46 } 47 int main() 48 { 49 //freopen("eccentric.in","r",stdin); 50 //freopen("eccentric.out","w",stdout); 51 scanf("%d%d",&n,&p); 52 getpri(2*n); 53 for(int i=1;i<=n;i++)calc(i,-1); 54 for(int i=n+2;i<=2*n;i++)calc(i,1); 55 int ans=1; 56 for(int i=2;i<=n*2;i++) 57 { 58 ans=(ll)ans*poww(i,cnt[i],p)%p; 59 } 60 printf("%lld\n",ans); 61 //fclose(stdin); 62 //fclose(stdout); 63 return 0; 64 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号