XXII Open Cup : Grand Prix of Southeastern Europe

QOJ，Editorial

A. ABC Legacy

我们可以求出三种子序列各划分出了多少个，设为 \(x,y,z\)，则 \(cnt_A=x+y\)，\(cnt_B=x+z\)，\(cnt_C=y+z\)，不难求出 \(x,y,z\)。从 \(B\) 出发考虑，它要作为 \(BC\) 出现 \(z\) 次，作为 \(AB\) 出现 \(x\) 次。显然将前 \(z\) 个 \(B\) 作为 \(BC\) 出现最优，此时 \(C\) 一定取某个 \(B\) 后面第一个没匹配的 \(C\)，这样做完以后只需要 check 一遍 \(AC\) 是否合法。

B. New Queries On Segment Deluxe

考虑没有可持久化怎么做。注意到 \(k\) 很小，尝试对列建立线段树然后维护所有行的信息，需要维护区间最小值，修改操作需要加法标记和赋值标记，下传标记的时候区间最小值并不是很好更改。对于行的每个子集，维护其和的最小值，这样区间最小值信息是好修改的，同时注意到子集信息也是可以相互推出的。时间复杂度 \(O(q\log n2^k)\)，最后加一个主席树即可。

C. Counting Phenomenal Arrays

一个直观感觉是，\(>1\) 的数不会很多，实际上确为如此。考虑对于所有 \(>1\) 的数求出 \(x=\prod-\sum\)，那么需要添加 \(x\) 个 \(1\) 使其合法。注意到数组里面的数是 \(O(n)\) 级别，更确切地可以分析到 \(\leq n\)，\(ab-a-b\geq 2(n+1)-2-(n+1)\geq n-1\)。感受到不断加入 \(>1\) 的数后 \(\prod-\sum\) 增长速度非常快，于是后面直接搜即可。

D. LIS Counting

问题的结构非常复杂，用双射来简化问题，题目中 \(NM\) 的形式提示映射到矩阵。下文 \(i\) 均指下标，\(p_i\) 指值。

令 \(inc_i\) 代表以 \(i\) 结尾的 LIS 长度，\(dec_i\) 代表以 \(i\) 结尾的 LDS 长度，可以说明，在同一个序列中 \((inc_i,dec_i)\) 互不相同。设 \(i<j\)，分析一下 \(p_i\) 和 \(p_j\) 的大小关系即可。

建立两个矩阵，\(A_{inc_i,dec_i}=i\)，\(B_{inc_i,dec_i}=p_i\)。考察矩阵的性质，可以发现 \(A\) 行列均递增，\(B\) 行减列增。同时对于一个合法的长为 \(nm\) 的序列，\(A\) 和 \(B\) 一定均被填满，同时形成双射。\(p\to(A,B)\) 是单射很好说明，\((A,B)\to p\) 是单射需要说明任何 \((A,B)\) 均能生成合法的 \(p\)，说明此点后恰好生成一个是显然的。对于一对 \((A,B)\) 生成一个序列 \(p\) 后，可以说明其必然合法。

对于 \(i:1\to nm\)，依次将 \(A\) 中值为 \(i\) 的位置染色，可以发现任意时刻染色必然为包含右上角的，轮廓不存在凹陷的连通块。新加入 \(i\) 时，考虑其 \(inc_i\) 实际上是从先前连通块中找到值小于其且 \(inc\) 最大的位置，\(inc\) 最大表现为最靠下，从 \(B\) 出发考虑，新染色点的上方显然是一个合法的位置，同时不存在其它更靠下的合法位置，因为 \(B\) 是行减列增的。\(dec\) 的分析同理。

我们要求的 \(f(pos,val)\) 即为在 \(AB\) 同一个位置上分别为 \(pos\) 和 \(val\) 的矩阵数量。对上面的染色过程 dp，维护轮廓线，可以统计出 \(g_0(i,j,pos)\) 代表 \(A_{i,j}=pos\) 的方案数，由于 \(AB\) 完全独立，各做一遍然后乘起来即可。对 \(B\) 的 dp 顺序需要从右上角开始。时间复杂度 \(O(\binom{n+m}nnm+(nm)^3)\)。

E. Flood Fill

建图。注意到有边的两个连通块在最后的矩阵中不可能同时被改变颜色，同时选择原图的一个独立集，钦定这些连通块改变颜色是一定可以做到的，图是二分图，所以问题等价于二分图最大独立集，网络流即可。

F. to Pay Respects

考虑什么时候让对手中毒最优，如果存在一个让对手中毒的时刻 \(i\)，同时对手存在一个回血的时刻 \(j\)，且 \(j\) 上没有中毒，\(i>j\)，那么将 \(i\) 上的中毒移到 \(j\) 一定更优，因为中毒本身就是越往前越优，唯一制约其的就是抵消回血这一效果。因此最后的中毒时间形如一段前缀加上若干回血的时间点，枚举最后一个中毒的时间即可。

G. Replace Sort

对 \(B\) 排序。考虑将 \(A\) 中的若干连续段替换成 \(B\) 的一个连续段，令 \(f_i\) 代表 \(i\) 处没有连续段的最小值，\(i-1\) 处没有连续段的情况可以直接转移。以下讨论 \(i-1\) 处有连续段的情况。

我们必然是将 \(A_{i-1}\) 替换成 \(B\) 中小于 \(A_i\) 的最大值，需要满足这个值 \(>A_{i-1}\)。显然这个值在此前不会被使用。同理，设连续段开头为 \(j+1\)，将 \(A_{i-1}\) 替换为 \(B_x\)，那么整个连续段就是将 \(A_{j+1\sim i-1}\) 替换为 \(B_{x-(i-j)+2\sim x}\)，写出转移条件：

\[A_j<B_{x-(i-j)+2}\&\&j\geq i-x-1 \]

第一个条件主要体现在下标上，考虑将其转化。设 \(c_i\) 为最小的 \(j\) 使得 \(A_i<B_j\)，若不存在则为 \(\infty\)，那么条件改写为：

\[c_j\leq x-(i-j)+2\Longrightarrow c_j-j\leq x-i+2 \]

这是唯一的条件，因为原先的第二个条件被此蕴含。线段树直接优化即可，时间复杂度 \(O(n\log n)\)。存在常数更小的做法，注意到 \((c_j-j,f_j)\) 带来了很多支配对，删掉不需要的支配对以后可以发现剩下的决策点一定是最大的 \(c_j-j\) 带来，set 维护即可。

H. Werewolves

枚举颜色 \(i\)，考虑组合意义。将 \(c_j=i\) 的点权设为 \(1\)，否则设为 \(-1\)，等价于查询树上权值 \(>0\) 的连通块数量，根据树上背包经典结论，做这个的复杂度是 \(O(nk)\)，其中 \(k\) 是颜色 \(i\) 的出现次数，总复杂度 \(O(n^2)\)。

I. Colourful Permutation Sorting

存在最优方案使得所有操作一在操作二之前。考虑最终序列的形态，如果一些数所处的颜色改变了，那么交换这些数是必然需要的，先将这些交换做完，此后的交换只会发生在同种颜色间，每种颜色是独立的，那一种颜色先做操作二在做操作一显然不优。同时每种颜色只会做一次操作二。

不存在操作二时的经典结论是答案为 \(n-cyc\)，\(cyc\) 为置换环数量。枚举哪些颜色做操作二，每个颜色的所有点可以缩成一个大点，我们想最大化图上的环数，每条边只能位于一个环中。缩掉二度点，则剩下最多 \(k\) 个点，同时每个点入度等于出度。自环直接删去，二元环也直接删去。三元环不能直接删去的原因是，假设最终答案中三条边在不同的环上，那么将三条边放在同一个环中，剩下三个缺一条边的环可能只合成一个环，环数减小。

实际上，如果我们能按顺序删去自环、二元环、三元环、四元环、五元环，那么是对的。上面的分析需要三条边在最终答案中处于不同的环，这些环至少是三元环（二元环和自环已经被删去了），那么顶点数至少是 \(6\)，由于最多 \(5\) 个点，所以必然有重复的顶点，可以多拆出一个简单环。四元环同理但复杂一点，四条边在不同环中的情况和上面一样，四条边在三个环中，顶点数至少为 \(12\)，肯定可以多拆出一个简单环。

还有一些别的做法。当不超过 \(4\) 个点的时候，一定可以找到一个点满足出点只有一个，合并即可。五个点的时候可以构造出如下反例（题解说每个点的入点数和出点数都为 \(2\)，下面这张图显然是不符合的，我也不知道是不是 typo）：

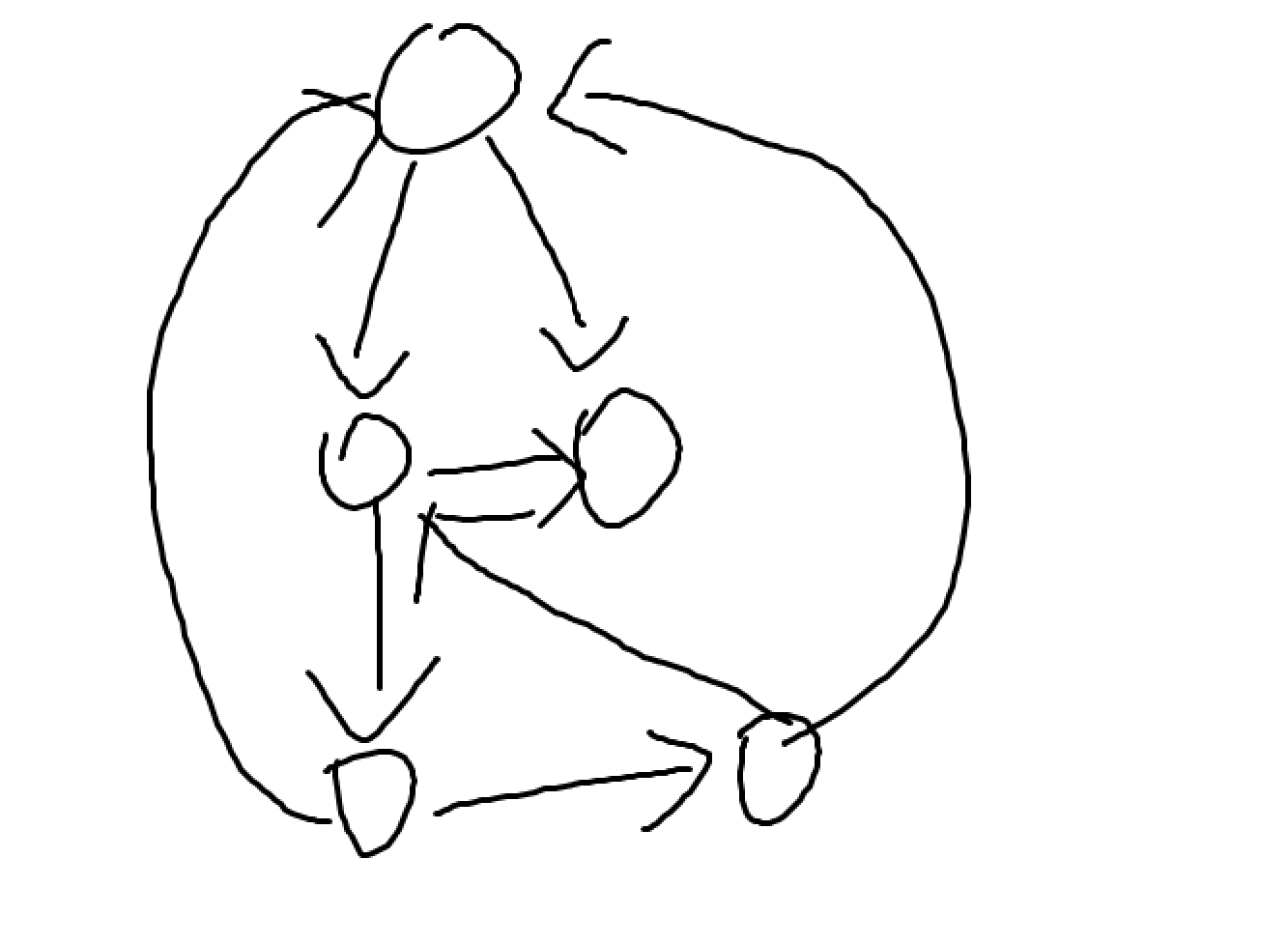
但是一定有出点数为 \(2\) 的点，暴力枚举配对方式可以缩掉这个点。其实我也不知道这句话是什么意思，看不懂。

上述所有过程都要不断删去自环和二元环。

J. Jason ABC

答案显然不超过 \(3\)，只需判断答案是否为 \(0\) 或 \(1\) 或 \(2\)。但是判断为 \(2\) 十分困难，实际上答案可以进一步分析到不超过 \(2\)。考虑最靠前的一个位置，满足这个位置是某种颜色的第 \(n\) 次出现，则通过将后面的位置染色可以做到两次操作。

\(0\) 次操作容易判断。考虑判断能否在 \(1\) 次操作内完成，枚举这次操作改变哪个颜色，扫描右端点，则可以直接得到左端点的位置，判断即可。

K. Amazing Tree

定根以后怎么做？找到最小的叶子，走到那里。可以发现最终答案的第一个数一定是最小的一度点，设为 \(u\)，其相连的点为 \(v\)。记录完 \(u\) 后需要走到 \(v\)，此时有两种情况：

• \(v\) 是根，对 \(v\) 的所有子树（除了 \(u\)）按照“子树内最小叶子”这一关键字进行 dfs。
• \(v\) 不是根，对 \(v\) 的所有子树（除了 \(u\) 和根方向）按照“子树内最小叶子”这一关键字进行 dfs。

由于可以随意定根，要是 \(v\) 不是根，我们一定会将根定在最小叶子最大的那个子树中，因此大部分 dfs 的顺序是固定的，先将所有不是最小叶子最大的子树 dfs 完。此时可以判断 \(v\) 是根优秀还是不是更优秀，如果是就做完了。如果不是，只需要往根的方向走一步，重复该过程。当走到一个一度点后，直接将根定为那个点即可。

L. Primes and XOR? Nonsense

显然，这道题唯一的突破口是我们认为素数相当随机。对值域分块，每块为 \([x\times 2^k,(x+1)\times 2^k)\)，即每个质数不一样的只有中间 \(k-1\) 位（最后一位均为 \(1\)，\(2\) 特殊处理），我们断言，当 \(k\) 充分大时，一定可以张成这个 \(k\) 维的空间。因此整块可以直接写出线性基，散块暴力求线性基。\(k\) 需要至少取到 \(11\) 才能保证正确性。

M. Many LCS

肯定需要去控制 LCS 的形态。考察如下字符串：

\[S=0^{k_1}010^{k_2}\dots0^{k_t}01 \]

\[T=(01)^{n+t} \]

\[\sum k_i\geq n \]

考虑 LCS 是什么，\(S\) 有若干段 \(0\)，中间用 \(01\) 分开，设 \(T\) 的某一段用一堆 \(0\) 匹配了 \(S\) 的某一段，令 \(P=\rm{LCS}(S,T)\)，这样 \(P\) 被划分为了若干段，每段可能为空，第 \(i\) 段匹配了 \(S\) 的第 \(i\) 段，可以说明 \(P\) 的相邻段中间也会被 \(01\) 隔开。如果不是的话一定可以调整。也就是说：

\[P=0^{a_1}010^{a_2}01\dots0^{a_t}01 \]

\[0\leq a_i\leq k_i \]

再来表示 LCS 长度，由形态得到长度为 \(n+2t\)。计算方案数时需要钦定若干个 \(T\) 中的若干个 \(01\) 段作为分隔，同时每段要短于 \(S\) 的对应段。这个计数很难做到一个很好的形式，不过要是 \(k_i\geq\frac n2\)，我们能通过容斥得到一个不错的式子：

\[\binom{n+t-1}{t-1}-\sum\limits_{i=1}^t\binom{n+k_i-1+t-1}{t-1} \]

后面的部分钦定 \(i\) 这一段满足 \(a_i>k_i\)，则其余的 \(a\) 必然合法，考虑先将一个长为 \(n+t-k_i-1\) 的段插完分割点，然后在 \(i\) 处插入一个长为 \(k_i+1\) 的段。我们通过取合适的 \(n,t,k_i\) 来让这个式子 \(=K\)。

往后的想法大致是找到一个固定的 \(t\)，然后求出一个 \(n\) 使得 \(\binom{n+t-1}{t-1}>K\)，背包出后面的部分。取 \(t=3\) 的话 \(n\approx\sqrt{2K}\)，取 \(t=4\) 则 \(n\approx\sqrt[3]{6K}\)，这已经很有道理了。背包的正确性来源于一个 open problem，任何一个数都能被表示成不超过五个 四面体数 之和，在 \(\leq 10^{10}\) 内已经被验证。不过我们的 \(t=4\)，而最少需要表示成五个四面体数的数字在范围内只有 \(241\) 个，对于这些数，我们重新选一个 \(n\) 做背包。

还需要保证 \(k_i\geq\frac n2\)，对于足够大的 \(K\) 这一定可以保证。对于较小的 \(K\)，尝试 \(t=2\) 和 \(t=3\) 对其构造即可。

N. Max Pair Matching

将每个点看作一条 \([l_i=\min(a_i,b_i),r_i=\max(a_i,b_i)]\) 的线段，则问题等价于钦定 \(n\) 条线段贡献 \(r_i\)，另外 \(n\) 条线段贡献 \(-l_i\)，同时后者在左端点处视为左括号，前者在右端点处视为右括号，需要是一个合法的括号序列。二选一，先钦定所有线段都贡献 \(r_i\)，此时选中一个线段的贡献就是 \(-r_i-l_i\)。一个贪心是从大到小选，这一定保证了一个合法括号序列。考虑将后面的左括号调整到前面可以说明。最终括号序列的形态一定是 ((((...))))。