BUAA-OO2022-UNIT1总结
一、前言
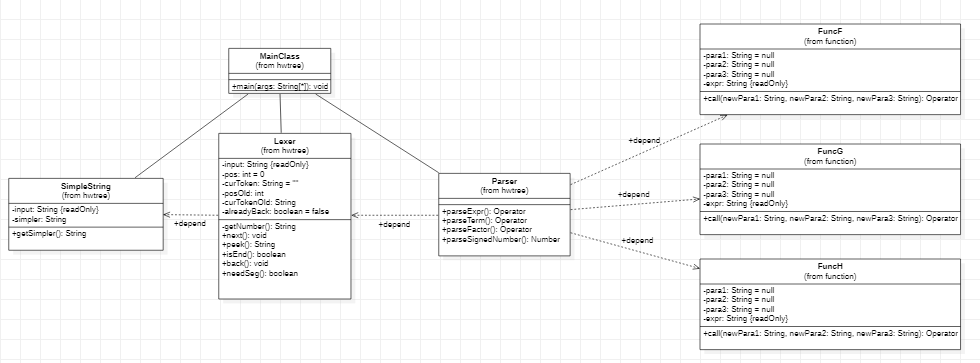
本单元主要是表达式的拆分和化简。个人认为相比于pre有很大的难度提升,特别是第一周,一开始就涉及到不小的工程量,在还没有熟悉java的情况下有不小的难度。第二周和第三周难度跨度略微下降。本人在第一周就看来许多往届学长的博客,重构了两次,选取了一个较为合理的构架,使得在之后两周后能够进行“”“增量”作业,而不需要重构。三次架构的基本框架都身份类似,故第二三次作业在架构部分主要只说与之前进行了那些改动
二、架构设计
第一次作业
-
基本思想:递归下降——建立二叉树形结构
解析:
![]()
存储结构:(存储即递归计算)
![]()
-
解析输入
- lexer负责字符串指针的移动和字符的弹出
- Parser递归得解析字符串,递归下降生成表达式树
Operator 解析Expr{ Operator left = 解析Term(); while (lexer弹出-) if (lexer弹出+) { Oprator right = 解析Expr(); } else if (lexer弹出+) { …… } return expr } Operator 解析Term{...} Operator 解析Factor{...} ...... -
存储结构层次逐渐下降
- 所有存储类都继承自“运算子”类——Operator。
- 拥有left right两个成员,都是Operator类。
- 拥有一个getResult函数计算两个子树运算后所得值。返回一个MAP——每个次数对应系数。eg:3x**2+2x+23,则
- 拥有一个toString函数,根据getResult方法得到的结果(一个HashMap)编写输出。所有继承Operator的类都可通用。
- 专门设计了一个result类用来存储每个运算子对象的值——主要是HashMap的处理。
- 最上层:表达式类Expr
- 拥有left right两个成员,getResult方法进行加法运算
- 中间层:项类Term
- 拥有left right两个成员,getResult方法进行乘法运算
- 因子接口:虽然最初设计了,但最后里面全删完了。
- 最底层:因子类:变量因子,常数因子,表达式因子:(xxx)**xxx(与表达式类不同)
- 根据不同情况设计,继承的left和right两个成员不一定有实际意义
- 表达式因子存储时若带指数则拆一层出来,left存一个普通表达式类,right存一个指数减一的表达式因子。getResult方法类似Term类的乘法运算。
- 所有存储类都继承自“运算子”类——Operator。
第二次作业迭代思路:
-
需求变更:增加了三角函数、自定义函数、求和函数
-
基本思想:仍然是递归下降——建立二叉树形结构
解析:
![]()
存储结构:
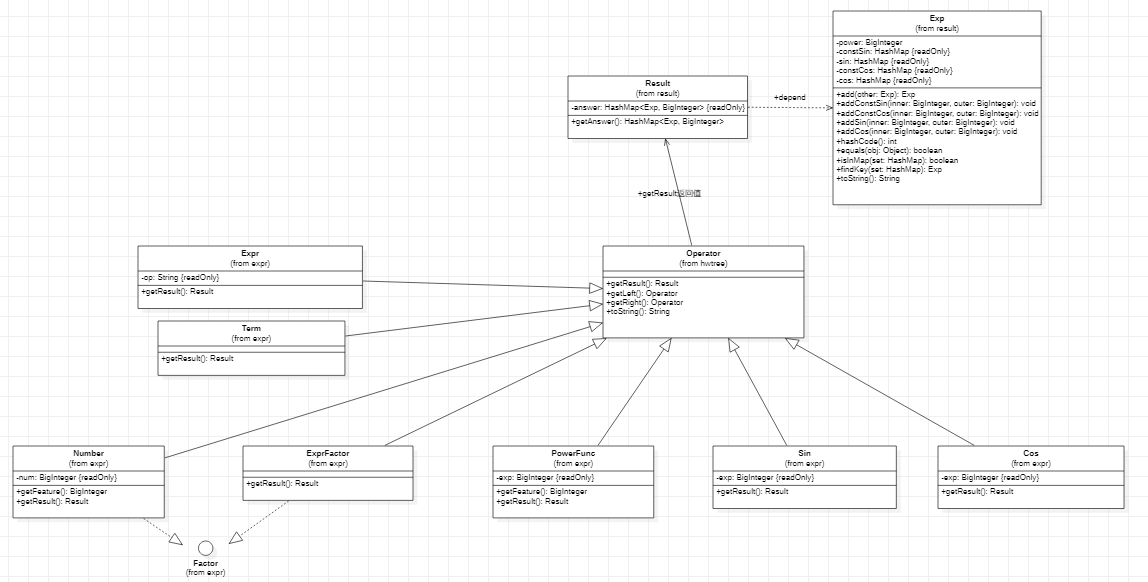
1、引入三角函数后更改存储形式
第一次作业的Result类:

- 使用一个HashMap<Integer, BigInteger>进行结果存储——{指数:系数}的格式。
第二次作业的Result类:

- Result类仍使用一个HashMap进行结果存储,但对于指数的存储新建了一个类——Exp类。
- Exp类中用5个属性来表示幂次项和三角函数项。
- Exp类需重写equals和hashcode函数来确保值比较不会出错。
2、sum函数因子的处理
- 将sum函数作为因子Factor层级,在递归下降处理表达式中,与表达式因子、三角函数同级
- 具lexer中设计识别sum函数的判断,可将求和表达式一次性全部读出
- 利用replace字符串替换函数把求和表达式中的i替换成实际循环变量值,进行循环相加。
- 相当于重新解析一个新的表达式,最终返回一个表达式类的对象。
3、自定义函数的处理
- 直接新建了三个类表示自定义函数f,g,h
- 将sum函数作为因子Factor层级,在递归下降解析表达式中,与表达式因子、三角函数同级
- 利用replace字符串对实参和形参进行替换,之后重新解析得到的“新”表达式
- 返回一个表达式类的对象
第三次作业迭代思路
- 架构与第二次完全相同,故不再重复类图
- 删除了没有什么实际意义的Factor类
1、嵌套函数:作业二实现
2、三角函数因子为表达式因子
更改Exp指数类中的存储结构。
第二次作业的Exp类属性:

第三次作业的Exp类属性:

- 改为用String来表示三角函数内层的内容
- 刚好每个类都有toString函数,可用来判断是否相等。
3、三角函数的化简
- 由于时间关系只完成了基本的合并同类项化简,没有进行sin**2+cos**2=1和二倍角一类的化简。
- 合并同类项主要在于对Exp类的比较,通过在Exp中编写equals方法实现,之后需要合并同类项的时候都不再需要根据具体运算子是Expr类还是Term类之类的进行不同考虑。耦合度很小,个人感觉很方便。
三、度量分析
缩写含义:
- OC:类的非抽象方法圈复杂度,继承类不计入
- WMC:类的总圈复杂度
- CogC:认知复杂度,衡量一个方法的控制流程有多困难去理解。具有高认知复杂度的方法将难以维护。
- ev(G):非抽象方法的基本复杂度,用以衡量一个方法的控制流结构缺陷,范围是 [1, v(G)]
- iv(G):方法的设计复杂度,用以衡量方法控制流与其他方法之间的耦合程度,范围是 [1, v(G)]
- v(G):非抽象方法的圈复杂度,用以衡量每个方法中不同执行路径的数量
- 圈复杂度:也称条件复杂度,衡量衡量一个模块判定结构的复杂程度,其数量上表现为独立路径的条数,也可理解为覆盖所有的可能情况最少使用的测试用例个数
第一次作业
规模分析:

相比于其他同学我的第一次规模应该要大一些,主要是由于选用了较为复杂的架构,但我的架构拥有较好的可拓展性,第二三次都在此基础上完成,我认为总的来说是利大于弊的。
但是要注意还是存在不少的重复代码,说明在设计上还存在一些耦合度较高的部分。
复杂度分析:
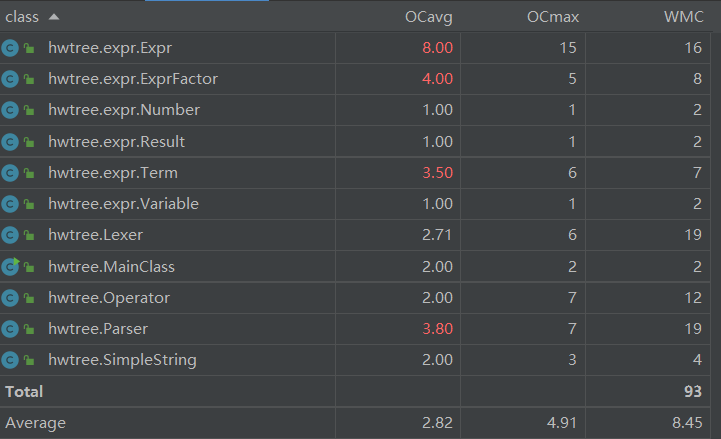
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| hwtree.expr.Expr.Expr(Operator, Operator, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Expr.getResult() | 34.0 | 6.0 | 15.0 | 15.0 |
| hwtree.expr.ExprFactor.ExprFactor(Expr, int) | 2.0 | 1.0 | 1.0 | 3.0 |
| hwtree.expr.ExprFactor.getResult() | 8.0 | 2.0 | 4.0 | 5.0 |
| hwtree.expr.Number.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Result.getPoly() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Result.Result(HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Term.getResult() | 9.0 | 3.0 | 4.0 | 6.0 |
| hwtree.expr.Term.Term(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Variable.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Variable.Variable(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.back() | 3.0 | 3.0 | 1.0 | 3.0 |
| hwtree.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Lexer.isEnd() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.needSeg() | 7.0 | 5.0 | 7.0 | 8.0 |
| hwtree.Lexer.next() | 7.0 | 3.0 | 7.0 | 12.0 |
| hwtree.Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.MainClass.main(String[]) | 2.0 | 1.0 | 2.0 | 2.0 |
| hwtree.Operator.getLeft() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getRight() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.toString() | 13.0 | 1.0 | 9.0 | 9.0 |
| hwtree.Parser.parseExpr() | 7.0 | 3.0 | 5.0 | 5.0 |
| hwtree.Parser.parseFactor() | 15.0 | 4.0 | 8.0 | 8.0 |
| hwtree.Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Parser.parseSignedNumber() | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Parser.parseTerm() | 5.0 | 4.0 | 2.0 | 4.0 |
| hwtree.SimpleString.getSimpler() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.SimpleString.SimpleString(String) | 4.0 | 1.0 | 3.0 | 4.0 |
| Total | 121.0 | 57.0 | 92.0 | 108.0 |
| Average | 3.6666666666666665 | 1.7272727272727273 | 2.787878787878788 | 3.272727272727273 |
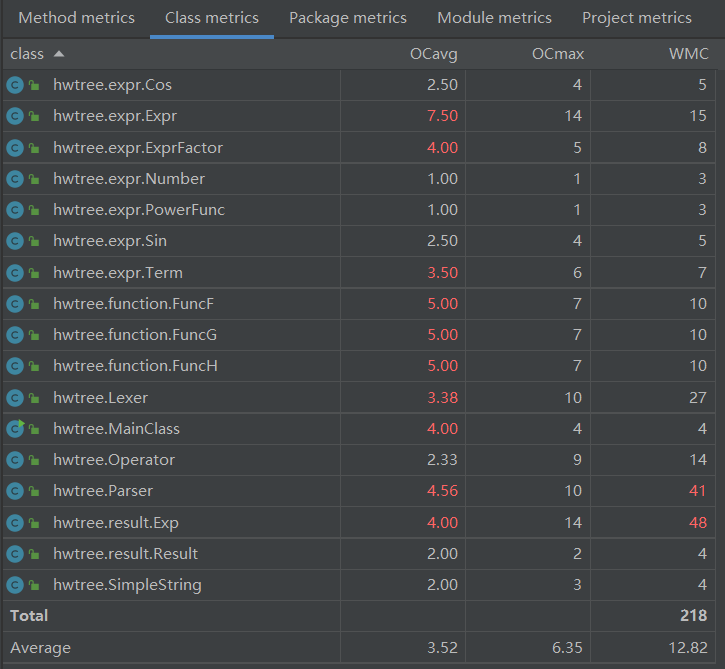
第二次作业
规模分析:
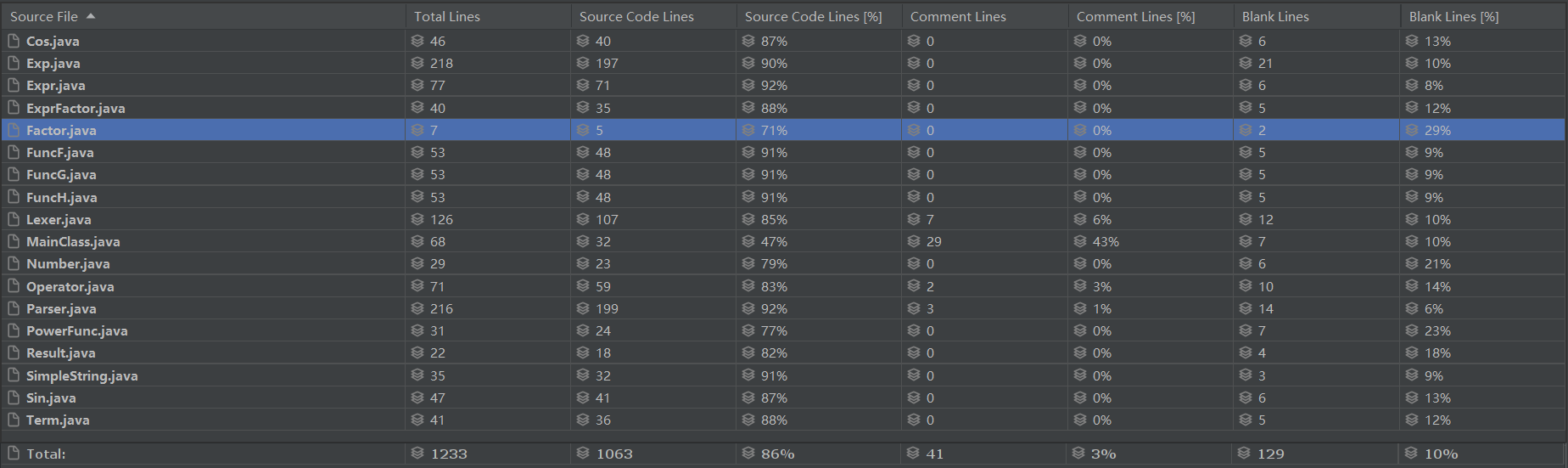
可以看出总行数达到了1233行,偏多;而且重复行也达到了43行,说明还是存在不少冗余的部分,设计上还不够精炼,存在“硬编程”,解耦度不够。
复杂度分析:
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| hwtree.expr.Cos.Cos(Factor, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Cos.getResult() | 5.0 | 4.0 | 4.0 | 4.0 |
| hwtree.expr.Expr.Expr(Operator, Operator, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Expr.getResult() | 30.0 | 6.0 | 14.0 | 14.0 |
| hwtree.expr.ExprFactor.ExprFactor(Expr, BigInteger) | 2.0 | 1.0 | 2.0 | 3.0 |
| hwtree.expr.ExprFactor.getResult() | 8.0 | 2.0 | 4.0 | 5.0 |
| hwtree.expr.Number.getFeature() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Number.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.getFeature() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.PowerFunc(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Sin.getResult() | 6.0 | 4.0 | 4.0 | 4.0 |
| hwtree.expr.Sin.Sin(Factor, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Term.getResult() | 9.0 | 3.0 | 4.0 | 6.0 |
| hwtree.expr.Term.Term(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.function.FuncF.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncF.FuncF(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.function.FuncG.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncG.FuncG(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.function.FuncH.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncH.FuncH(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Lexer.back() | 3.0 | 3.0 | 1.0 | 3.0 |
| hwtree.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Lexer.getSumExpr() | 5.0 | 1.0 | 4.0 | 5.0 |
| hwtree.Lexer.isEnd() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.needSeg() | 7.0 | 5.0 | 7.0 | 8.0 |
| hwtree.Lexer.next() | 16.0 | 3.0 | 12.0 | 23.0 |
| hwtree.Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.MainClass.main(String[]) | 5.0 | 1.0 | 3.0 | 4.0 |
| hwtree.Operator.getLeft() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getRight() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.toString() | 25.0 | 1.0 | 13.0 | 13.0 |
| hwtree.Parser.parseExpr() | 7.0 | 3.0 | 5.0 | 5.0 |
| hwtree.Parser.parseFactor() | 19.0 | 7.0 | 14.0 | 14.0 |
| hwtree.Parser.parseFunc() | 7.0 | 3.0 | 6.0 | 7.0 |
| hwtree.Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Parser.Parser(Lexer, FuncF, FuncG, FuncH) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Parser.parseSignedNumber() | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Parser.parseSumFunc() | 4.0 | 2.0 | 3.0 | 3.0 |
| hwtree.Parser.parseTerm() | 5.0 | 4.0 | 2.0 | 4.0 |
| hwtree.Parser.parseTri() | 5.0 | 3.0 | 3.0 | 6.0 |
| hwtree.result.Exp.add(Exp) | 20.0 | 1.0 | 13.0 | 13.0 |
| hwtree.result.Exp.addConstCos(BigInteger, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.addConstSin(BigInteger, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.addCos(BigInteger, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.addSin(BigInteger, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.equals(Object) | 7.0 | 8.0 | 1.0 | 8.0 |
| hwtree.result.Exp.Exp() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.Exp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.findKey(HashMap) | 3.0 | 3.0 | 2.0 | 3.0 |
| hwtree.result.Exp.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.isInMap(HashMap) | 3.0 | 3.0 | 2.0 | 3.0 |
| hwtree.result.Exp.toString() | 25.0 | 1.0 | 14.0 | 14.0 |
| hwtree.result.Result.getAnswer() | 1.0 | 1.0 | 2.0 | 2.0 |
| hwtree.result.Result.Result(HashMap) | 1.0 | 1.0 | 2.0 | 2.0 |
| hwtree.SimpleString.getSimpler() | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 264.0 | 111.0 | 208.0 | 244.0 |
| Average | 4.258064516129032 | 1.7903225806451613 | 3.3548387096774195 | 3.935483870967742 |
可以看出几个大方法的复杂度和耦合度都有些超标,同时也会发现这些方法都是主要出bug的地方。因此如何有效处理多种情况判断的需求、把大方法拆分成消防法、降低耦合度是需要思考之处。
此外,函数处理部分也存在明显的“硬编程”,因为题目需求而直接设置三个类存储三种自定义函数,可以满足需求但可拓展性很低,判定结构也很冗杂,有不少改进的空间。
第三次作业
规模分析:
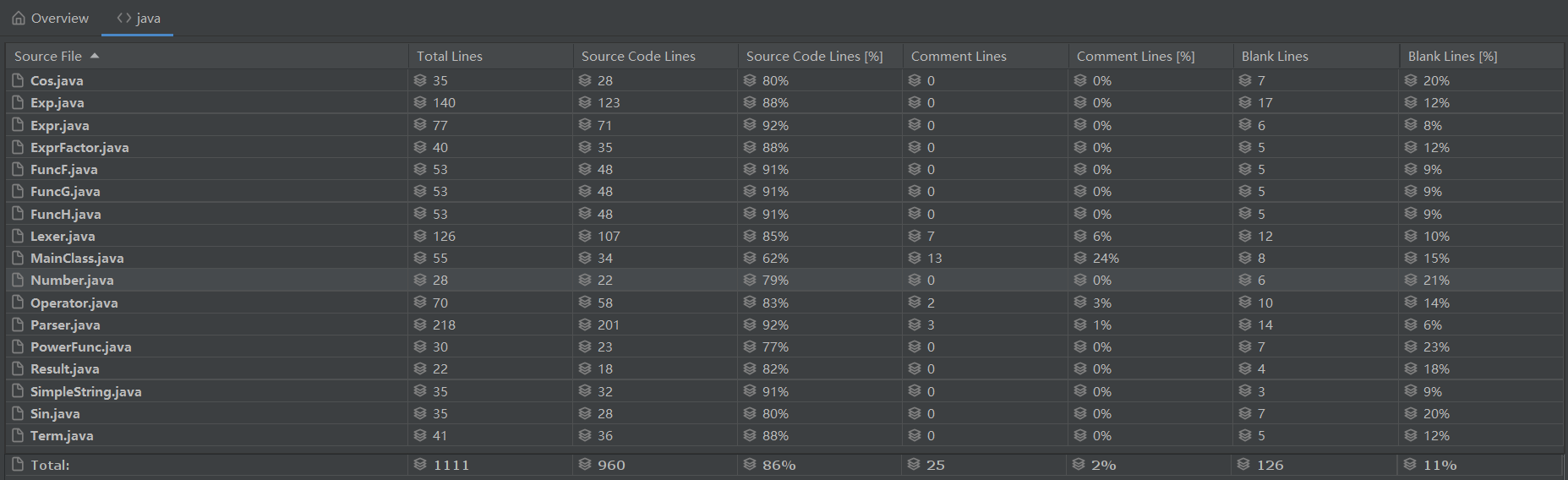
可以发现,第三次作业相比第二次总行数反而变少了,重复代码也减少。由此可以看出第三次利用String来存储sin和cos内部结构其实是一种更合理的方式,相比第二次的每种情况建一个哈希表,具有更好的可拓展性、并且减小了耦合度。
复杂度分析:
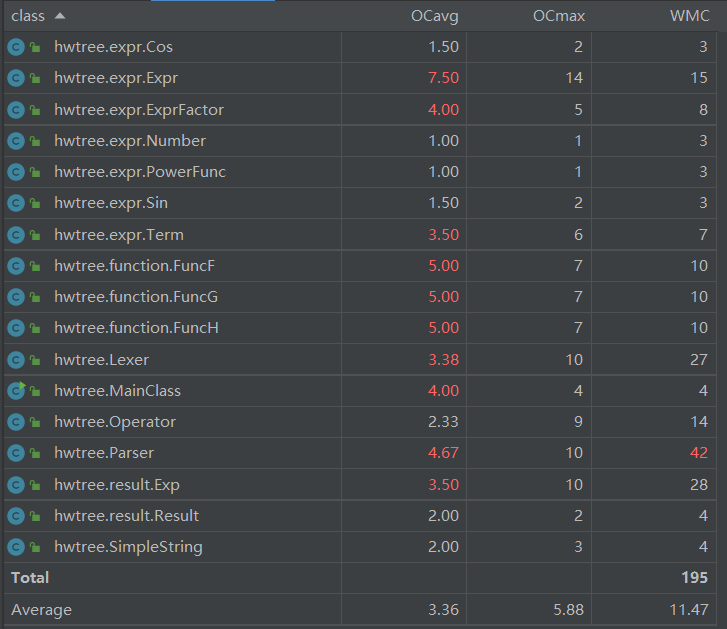
可以发现整体复杂度相较第二次有所下降,主要贡献者是两个三角函数类,这也得益于之前提到的String存三角函数内部是一种更好的方式。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| hwtree.expr.Cos.Cos(Operator, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Cos.getResult() | 1.0 | 2.0 | 2.0 | 2.0 |
| hwtree.expr.Expr.Expr(Operator, Operator, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Expr.getResult() | 30.0 | 6.0 | 14.0 | 14.0 |
| hwtree.expr.ExprFactor.ExprFactor(Expr, BigInteger) | 2.0 | 1.0 | 2.0 | 3.0 |
| hwtree.expr.ExprFactor.getResult() | 8.0 | 2.0 | 4.0 | 5.0 |
| hwtree.expr.Number.getFeature() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Number.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.getFeature() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.PowerFunc.PowerFunc(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Sin.getResult() | 1.0 | 2.0 | 2.0 | 2.0 |
| hwtree.expr.Sin.Sin(Operator, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.expr.Term.getResult() | 9.0 | 3.0 | 4.0 | 6.0 |
| hwtree.expr.Term.Term(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.function.FuncF.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncF.FuncF(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.function.FuncG.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncG.FuncG(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.function.FuncH.call(String, String, String) | 6.0 | 1.0 | 7.0 | 7.0 |
| hwtree.function.FuncH.FuncH(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Lexer.back() | 3.0 | 3.0 | 1.0 | 3.0 |
| hwtree.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Lexer.getSumExpr() | 5.0 | 1.0 | 4.0 | 5.0 |
| hwtree.Lexer.isEnd() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Lexer.needSeg() | 7.0 | 5.0 | 7.0 | 8.0 |
| hwtree.Lexer.next() | 16.0 | 3.0 | 12.0 | 23.0 |
| hwtree.Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.MainClass.main(String[]) | 5.0 | 1.0 | 3.0 | 4.0 |
| hwtree.Operator.getLeft() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getResult() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.getRight() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.Operator(Operator, Operator) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Operator.toString() | 25.0 | 1.0 | 13.0 | 13.0 |
| hwtree.Parser.parseExpr() | 7.0 | 3.0 | 5.0 | 5.0 |
| hwtree.Parser.parseFactor() | 19.0 | 7.0 | 14.0 | 14.0 |
| hwtree.Parser.parseFunc() | 7.0 | 3.0 | 6.0 | 7.0 |
| hwtree.Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Parser.Parser(Lexer, FuncF, FuncG, FuncH) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.Parser.parseSignedNumber() | 3.0 | 1.0 | 3.0 | 3.0 |
| hwtree.Parser.parseSumFunc() | 6.0 | 2.0 | 4.0 | 4.0 |
| hwtree.Parser.parseTerm() | 5.0 | 4.0 | 2.0 | 4.0 |
| hwtree.Parser.parseTri() | 5.0 | 3.0 | 3.0 | 6.0 |
| hwtree.result.Exp.add(Exp) | 10.0 | 1.0 | 7.0 | 7.0 |
| hwtree.result.Exp.addCos(String, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.addSin(String, BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.equals(Object) | 5.0 | 6.0 | 1.0 | 6.0 |
| hwtree.result.Exp.Exp() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.Exp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.result.Exp.toString() | 19.0 | 1.0 | 14.0 | 14.0 |
| hwtree.result.Result.getAnswer() | 1.0 | 1.0 | 2.0 | 2.0 |
| hwtree.result.Result.Result(HashMap) | 1.0 | 1.0 | 2.0 | 2.0 |
| hwtree.SimpleString.getSimpler() | 0.0 | 1.0 | 1.0 | 1.0 |
| hwtree.SimpleString.SimpleString(String) | 4.0 | 1.0 | 3.0 | 4.0 |
| Total | 233.0 | 97.0 | 193.0 | 225.0 |
| Average | 4.017241379310345 | 1.6724137931034482 | 3.3275862068965516 | 3.8793103448275863 |
相关函数的复杂度也有所下降,原因与之前分析的相同。
四、测试方法与bug分析
1. 测试方法
由于时间关系只在第一次作业的时候自己写了一个评测程序用于评测。第二次和第三次增加了自定义函数、求和函数后自动测试样例的生成变复杂,因而没来得及写。
第一次作业评测机的思路:
-
自动生成代码
参考当时讨论区中王小鸽同学的思路,依据表达式的形式化表述,一层一层地递归生成测试用例。大致思路如下:
def get_num(type): # 常数 ans = "" # 随机加上± # …… ans += random.choice(string.digits) # …… return ans def get_variable(): # …… def get_expr_factor(termNum, factorNum, max_depth): # 表达式/因子 ans = "(" ans += get_expr(termNum, factorNum, max_depth) ans += ")" # 随机带指数 return ans def get_term(termNum, factorNum, max_depth): ans = "" # 随机加上± # 随机调用上方的函数生成多个因子,用*连接 return ans def get_expr(termNum, factorNum, max_depth): ans = "" # 随机加上± # …… ans += get_term(termNum, factorNum, max_depth) # …… return ans def cal(exp, x_value): x = x_value return eval(exp) -
测试
-
基本思路:
-
自动生成待化简表达式
-
在python中调用写好的java程序,获得结果my_out
-
随机代入x的值,利用eval函数进行计算,得到源表达式和java程序化简后表达式的数值结果
-
比较两个结果。
-
重复第一步
-
-
需要注意:
- 调用eval需要先对其中的常数项去除前导零
-
2. bug分析
以下是各次作业遇到的一些有启示性的bug。
第一次作业
-
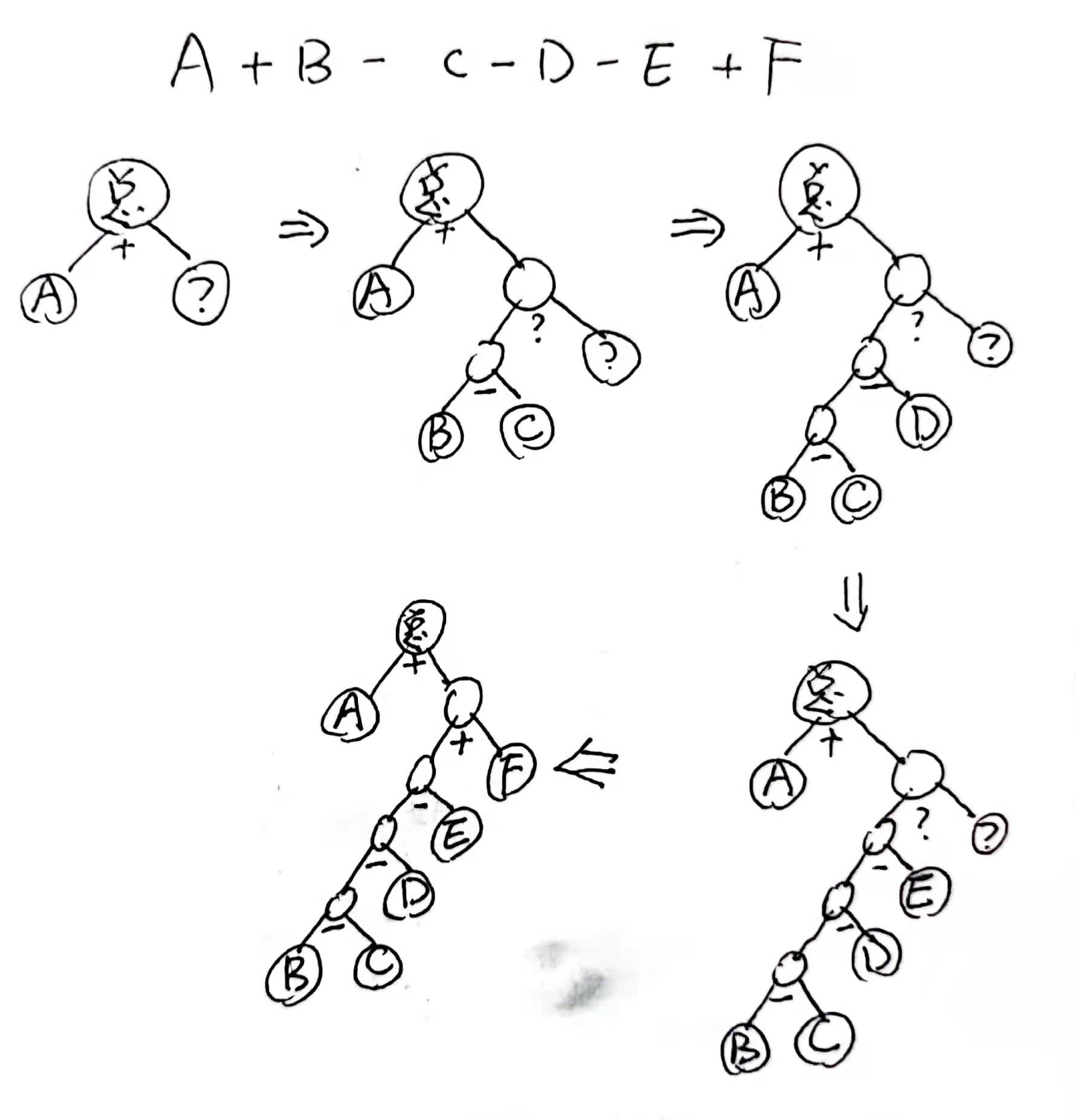
初期架构设计bug——无法处理连续减法。
- 例:5-2-3+4
-
原因:最初划分树形结构时若是读入一个+或-,则把其左右直接当成两个子节点,然而如果是减号,此种处理会把右侧全部都当做减数,相当于人为添加了一个括号。
-
改进:如果遇到减号,把左侧叫成节点1,把减号右侧紧邻的一个Term叫做节点2,新建节点3的左子节点为节点1,右子节点为节点2,把节点3当做总的左节点;若接下来又是减号,则按相同的思路把左节点变深一层,把右侧紧邻的Term添加到新左节点右子节点。可见图例:
![]()
-
输出为0
- 例:x-x
- 分析:需要在toString中进行一个特殊考虑
-
连续符号解析出错
- 例:- + -1
- 原因:以为解析的是带符号常数,建树时对“自带”符号处理不清晰
- 改进:利用replace方法把输出的所有连续符号转变为单一符号
-
一些nullpointer报错
- 例:-x**2-x**+0*x*-389161*x*+767+8*x**+3*x-2831468*+39
- 分析:Expr类、Term类内进行运算的时候子节点很可能是null,需要充分判断!
第二次作业
- sin(x)**0 - 0 * cos(1) + - x**2 被hack
- 分析:sin和cos里面对外指数为0的情况把Exp的power设成了1
- sin(0)**0 hack别人
- 分析:遇到sin(0)先处理成了0,但是若外层指数也为0的话整体应该为1
第三次作业
- sum函数的上下界问题
- 例:x*sum(i,1,0,0)
- 原因:若是出现上界小于下届整个因子应该为0,但设计时容易设计一个for循环,此时若出现上界小于下届会直接退出循环而返回一个null作为子节点。
- 改进:增加if判断是否需要返回0
- sum爆int问题
- 例:x*sum(i,12345678912,12345678913,0)
- 分析:对于这种不定的常数一定要充分考虑,宁愿都设成BigInteger!
五、心得体会
这一单元的作业算是面向过程思想到面向对象思想的转变。本单元作业在第一单元就经历了多次重构,选取了一个较好的架构,耦合度较小、可拓展性强。因而后续的几次作业都较为游刃有余,通过一些增补和修改可以较好得适应新功能。
但是本次在评测方面则显得不足。除了第一单元写了评测程序,后续都没有在评测上下功夫。并且测试的时候总是懒得从逻辑上去构思边界条件、不同可能的组合,导致思路混乱,不仅自己的第二次作业出现了不少弱智错误没检查出来,互测也只是随机地编数据,没有针对性,十分低效。如果能够稍微花点时间理一下逻辑,画几个树状分类图,相信可以事半功倍。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号