Codeforces Round #460 (Div. 2) E. Congruence Equation

E. Congruence Equation

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given an integer x. Your task is to find out how many positive integers n (1 ≤ n ≤ x) satisfy

where a, b, p are all known constants.

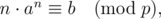
Input

The only line contains four integers a, b, p, x (2 ≤ p ≤ 106 + 3, 1 ≤ a, b < p, 1 ≤ x ≤ 1012). It is guaranteed that p is a prime.

Output

Print a single integer: the number of possible answers n.

Examples

input

2 3 5 8

output

2

input

4 6 7 13

output

1

input

233 233 10007 1

output

1

Note

In the first sample, we can see that n = 2 and n = 8 are possible answers.

 

思路：问题转化为n%(p - 1) = x, n % p = y, y = b / (a ^ x) % p, 枚举x，后一个式子通过递推预处理求出的逆元可以O(1)得到y的值，然后前两个式子孙子定理得到最小n，进而算出此时多少个X内的合法n。时间复杂度O(p)。有个不明白的地方是没特判p = 2的情况对结果居然没有影响。

#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <iomanip>
#include <cctype>
#include <cassert>
#include <bitset>
#include <ctime>

using namespace std;

#define pau system("pause")
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define clr(a, x) memset(a, x, sizeof(a))

const double pi = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-9;

ll a, b, p, x, ans;
ll mpow(ll x, ll y, ll MOD) {
    if (y <= 0) return 1;
    ll res = mpow(x, y >> 1, MOD);
    if (y & 1) {
        return res * res % MOD * x % MOD;
    } else {
        return res * res % MOD;
    }
}
ll pow_a[1000015], inv[1000015];
int main() {
    scanf("%lld%lld%lld%lld", &a, &b, &p, &x);
    pow_a[0] = 1;
    for (int i = 1; i <= p; ++i) {
        pow_a[i] = pow_a[i - 1] * a % p;
    }
    inv[1] = 1;
    for (int i = 2; i < p; ++i) {
        inv[i] = (p - p / i) * inv[p % i] % p;
    }
    ll m1 = p - 1, m2 = p, M = p * (p - 1), M1 = p, M2 = p - 1;
    ll inv_M1 = mpow(M1, m1 - 2, m1), inv_M2 = mpow(M2, m2 - 2, m2);
    for (int i = 0; i < p - 1; ++i) {
        ll y = inv[pow_a[i]] * b % p;
        ll res = (i * M1 * inv_M1 + y * M2 * inv_M2) % M;
        if (res > x) {
            continue;
        }
        ll tans = (x - res) / M;
        if (res) ++tans;
        tans = max(tans, 0ll);
        ans += tans;
    }
    printf("%lld\n", ans);
    return 0;
}