臭鼬牌圆锥曲线笔记(烂尾了)

进行一个圆锥曲线的笔记的整理。

由于现在不太成体系所以先散着记笔记。

一.圆锥曲线的介绍

1.椭圆、双曲线、抛物线定义

啊？不会有人知道椭圆、双曲线、抛物线定义来看这个吧？

椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

双曲线 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

抛物线 \(y^2=2px(p>0)\)

证明就不介绍了下一个。

2.基本处理技巧：

说实话我也不是很了解，但是浅浅总结一点点(毕竟除了我也没人看这么简单的东西吧……)。

对于选择题和填空题，一般来说都是让你使用二级结论秒杀不会联立方程求解。

而大题一般就是联立直线椭圆然后加上韦达定理解方程什么的。

而其他的处理技巧基本都是辅助韦达定理或者构造好的结构解决，由于方法太过于多了而且我也不会很多就先写一点点进行一个积累。

由于三种类型太多本人比较喜欢椭圆就都以椭圆为例。

基本的联立：

椭圆与直线的联立每道题都会用到，所以应该比较熟练，对于椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) 和直线 \(y=kx+m\) 联立，得到的方程应当是：

\[(a^2k^2+b^2)x^2+2a^2kmx+a^2(m^2-b^2)=0 \]

由于像是求线段长度这种东西常用 \(x_1-x_2\) 的值所以 \(\Delta\) 值也是常用的，应该熟悉。

\[\Delta=4a^2b^2(a^2k^2+b^2-m^2) \]

\[\sqrt{\Delta}=2ab\sqrt{a^2k^2+b^2-m^2} \]

双曲线和抛物线同理。

二.圆锥曲线的一车处理技巧

1.齐次化(处理斜率和积定值问题)

进行一个典中典例题的看：

已知椭圆 \(\frac{x^2}{4}+y^2=1\)，设不经过点 \((0,1)\) 的直线 l 与椭圆交于 B,C 两点，若 AB,AC 斜率之和为 -1，证明：直线 l 恒过定点。

别说我太菜了连这都不会，我就是菜怎么了。

首先是设直线 l，我们发现可以将直线方程设成：

\[mx+n(y-1)=1 \]

就可以表示所有不经过 \((0,1)\) 的直线了。

随后我们进行一个椭圆的处理。

\[\frac{x^2}{4}+y^2=1 \]

\[x^2+4y^2=4 \]

\[x^2+4(y-1+1)^2=4 \]

\[x^2+4(y-1)^2+8(y-1)=0 \]

注意到 \(8(y-1)\) 与其他项不齐次，考虑构造齐次：

\[x^2+4(y-1)^2+8(y-1)(mx+n(y-1))=0 \]

\[x^2+(4+8n)(y-1)^2+8mx(y-1)=0 \]

因为我们知道直线 l 的斜率 \(k=\frac{y-1}{x}\)，所以我们就有：

\[(4+8n)k^2+8mk+1=0 \]

\[k_1+k_2=-\frac{2m}{1+2n}=-1 \]

\[2m-2n=1 \]

\[y-1=-2 \]

\[x=2,y=-1 \]

所以直线 l 过定点 \((2,-1)\)，任务完成。

总结其核心在于：

• 1.不过点 \((x_0,y_0)\) 的直线系可以表示为 \(m(x-x_0)+n(y-y_0)=1\)。

• 2.对椭圆的处理可以恰好使得常数项为零(若不为零则点不在椭圆上)，进行一个元的换

更典例分析(2022 新高考 I 数学 21 题)：

过双曲线 \(\frac{x^2}{2}-y^2=1\) 上一点 \(A(2,1)\) 的两条直线斜率之和为 0，求两条直线与双曲线的两个交点所在直线的斜率(题目是我自己概括的)

我们利用同样的处理技巧：

\[m(x-2)+n(y-1)=1 \]

\[(x-2+2)^2-2(y-1+1)^2=2 \]

\[(x-2)^2+4(x-2)-2(y-1)^2-4(y-1)=0 \]

\[(x-2)^2-2(y-1)^2+4((x-2)-(y-1))(m(x-2)+n(y-1))=0 \]

\[(1+4m)(x-2)^2-(2+4n)(y-1)^2+(4n-4m)(x-2)(y-1)=0 \]

\[-(2+4n)k^2+(4n-4m)k+1+4m=0 \]

\[k_1+k_2=\frac{2n-2m}{1+2n}=0 \]

\[n=m \]

所以随便带个 \(n=m=1\) 进入得到 \(k=-1\)。

任务彻底完成。

2.第三定义(优化运算/二级结论)：

众所周知有个东西他叫第三定义，比如 \(A(2,0),B(-2,0)\)，一点 \(M\) 满足 \(k_{AM}k_{BM}=-\frac{1}{2}\)，求点 \(M\) 的轨迹。

这道题显然非常的没脑子，但是还是要写一下。

设 \(M(x_0,y_0)\)

\[k_{AM}k_{BM}=\frac{y_0^2}{(x_0-2)(x_0+2)}=-\frac{1}{2} \]

\[2y_0^2=4-x_0^2 \]

\[\frac{x_0^2}{4}+\frac{y_0^2}{2}=1 \]

但是注意到若 AM 或 BM 为通径时是不存在斜率的，所以要扣掉 4 个点。但是这并不妨碍我们使用这个美好的性质。

现在我们开始反过来考虑这个问题，如果我们知道 \(A(a,0),B(-a,0)\) 在椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) 上，那么椭圆上任意一点 \(M\)(AM,BM有斜率)的 \(k_{AM}k_{BM}\) 是否为定值，这个定值是多少？

我们显然发现：确实为定值。

\[\frac{y_0^2}{x_0^2-a^2}=\frac{y_0^2}{-\frac{a^2}{b^2}y_0^2}=-\frac{b^2}{a^2}=e^2-1 \]

通过证明你可以发现对于双曲线也满足(指 \(e^2-1\))

但是这个应用过于狭隘了，我们进行一个引理的获取。

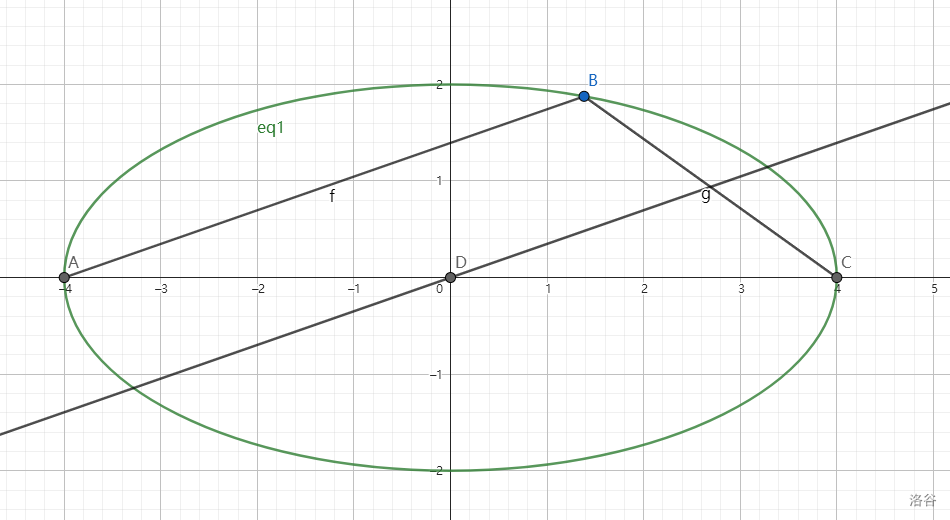
根据我们刚才的知识我们知道 \(k_{AB}k_{BC}=e^2-1\)，但是我们发现如果我们做一条中位线那么就得到了新的结论：

椭圆上两点 AB 和中点 M 满足 \(k_{AB}k_{OM}=e^2-1\)

进而我们还可以发现：

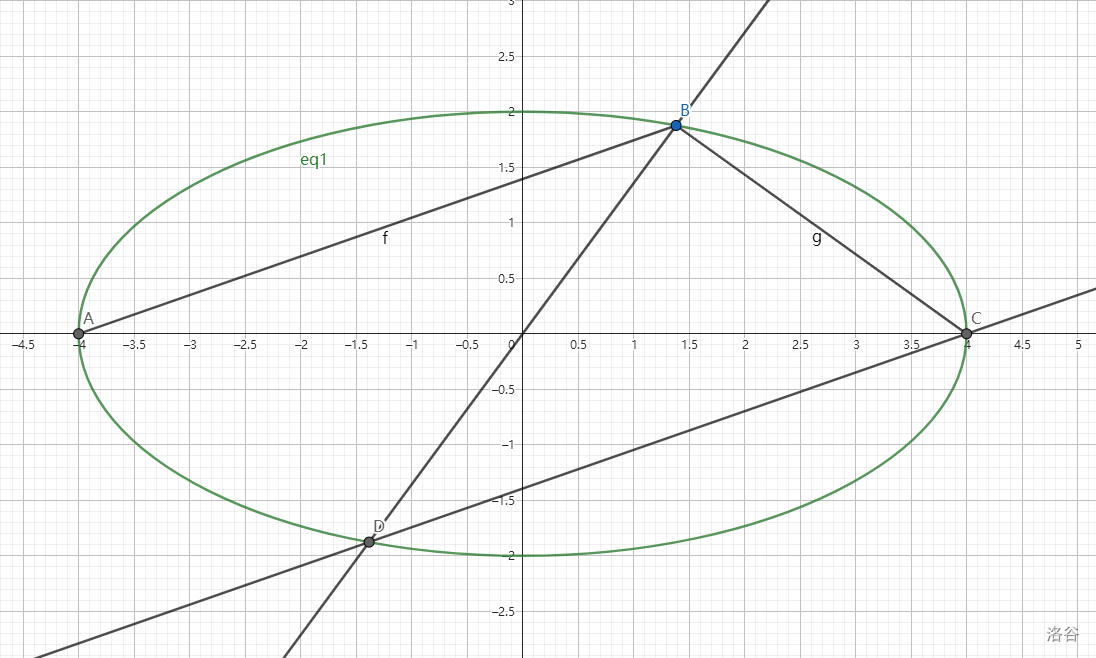
\(k_{BC}k_{CD}=e^2-1\)

所以我们就有：

对于过原点的直线 l 与椭圆交于两点 AB，顶点为 C 则 \(k_{AC}k_{BC}=e^2-1\)

特别注意如果焦点在 y 轴那么结论有所不同。

\[\frac{y_0^2}{a^2}+\frac{x_0^2}{b^2}=1 \]

\[\frac{y_0^2}{x_0^2-b^2}=-\frac{a^2}{b^2} \]

不用背过，带个特殊值算一下即可。

变式！求 \(a_n\) 前 n 项和！

对于椭圆 \(\frac{y^2}{4}+x^2=1\) 的过左顶点 \(A(-1,0)\) 和右顶点 \(B(1,0)\) 的两条直线 \(AM,BN\) 满足 \(\frac{k_{AM}}{k_{BN}}=2\) 且直线 \({MN}\) 过 \((0,1)\)，求直线 \(MN\) 方程。(好像是这么个东西)

注意到他给予的是斜率的比例而不是斜率的乘积这非常难搞，然后班里同学纷纷拿出了他们的非对称韦达然后算了一大堆最后算出来，但是伟大的臭鼬一眼就切掉了这道题，它使用了第三定义。

注意到 \(A,B\) 关于原点对称，所以可以得出结论 \(k_{AM}k_{BM}=-4\)

\[-\frac{4}{k_{BN}k_{BM}}=2 \]

\[k_{BN}k_{BM}=-2 \]

\[\frac{y_1}{x_1-1}\times\frac{y_2}{x_2-1}=\frac{y_1y_2}{x_1x_2-(x_1+x_2)+1}=-2 \]

哦这不是我们熟悉的常见的韦达定理吗！

直接进行一个立的联。

设 \(y=kx+1\) 并与 \(4x^2+y^2=4\) 联立。

\[(4+k^2)x^2+2kx-3=0 \]

\[x_1+x_2=-\frac{2k}{4+k^2} \]

\[x_1x_2=-\frac{3}{4+k^2} \]

\[y_1y_2=(kx_1+1)(kx_2+1)=k^2x_1x_2+k(x_1+x_2)+1 \]

\[\frac{-\frac{3k^2}{4+k^2}-\frac{2k^2}{4+k^2}+1}{-\frac{3}{4+k^2}+\frac{2k}{4+k^2}+1}=-2 \]

\[\frac{4-4k^2}{k^2+2k+1}=-2 \]

\[k^2-2k-3=0 \]

解得 \(k=3\) 或 \(-1\)

注意到若 \(k=-1\) 则过右顶点显然不合条件。舍 \(k=-1\)。

所以 \(y=3x+1\)。

(由于我之前也没有算过这道题只知道思路，所以可能写的有点繁琐)

点差法(中点弦)

说实话我觉得这个东西没什么大用，或许是因为第三定义太好用了。

他就是第三定义的另一种证明方法吧。

\[\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1 \]

\[\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1 \]

做差得：

\[\frac{(x_0+x_1)(x_0-x_1)}{a^2}+\frac{(y_0+y_1)(y_0-y_1)}{b^2}=0 \]

\[\frac{(y_0+y_1)(y_0-y_1)}{(x_0+x_1)(x_0-x_1)}=-\frac{b^2}{a^2} \]

观察上面的式子可以得到：

\[k_{AB}k_{CD}=-\frac{b^2}{a^2} \]

啊没有了，这就是全部内容，下一个。

啊不会真的以为就没了吧，还有 定比点差法

和点差法类似但是会有一个比例，其实个人觉得更像是加权点差法，无所谓反正差不多。

典中典例题：过椭圆 \(E=\frac{x^2}{2}+y^2=1\) 左焦点 \(F\) 的直线与椭圆交于 \(A,B\) 两点，且 \(\overrightarrow{FA}=3\overrightarrow{FB}\),求 \(A\) 点坐标。

我们利用和点差法一样的方式 \(A(x_1,y_1)\) 与 \(B(x_2,y_2)\) 均在椭圆上。

\[\frac{x_1^2}{2}+y_1^2=1 \]

\[\frac{x_2^2}{2}+y_2^2=1 \]

\[\frac{x_2^2\lambda^2}{2}+y_2^2\lambda^2=\lambda^2 \]

\[\frac{(x_2\lambda-x_1)(x_2\lambda+x_1)}{2}+(y_2\lambda-y_1)(y_2\lambda+y_1)=\lambda^2-1 \]

\[\frac{x_2\lambda+x_1}{\lambda+1}=-1 \]

\[\frac{y_2\lambda+y_1}{\lambda+1}=0 \]

\[x_1-x_2\lambda=\frac{\lambda^2-1}{2} \]

又因为我们刚才求出了：

\[x_1+x_2\lambda=-\lambda-1 \]

解得 \(x_1=\frac{\lambda^2-1}{2}-\lambda-1=0\)，\(A(0,1)\) 或 \((0,-1)\)。

极点极线(圆锥曲线内接四边形以及点在定直线)

这个东西有点点的高级，但是事先声明这个东西不太能在大题里面用，如果要大题用记得写假过程。

至于假过程，大概就是说你写个暴力的柿子，极其复杂的柿子，然后在草稿纸上用二级结论秒杀，然后写个解得。

首先我不太了解极点极限的定义是什么，但是通过各方了解，大概可以分为两种方式去引入这个问题。

首先第一种是利用调和点列去引入极点极线的。

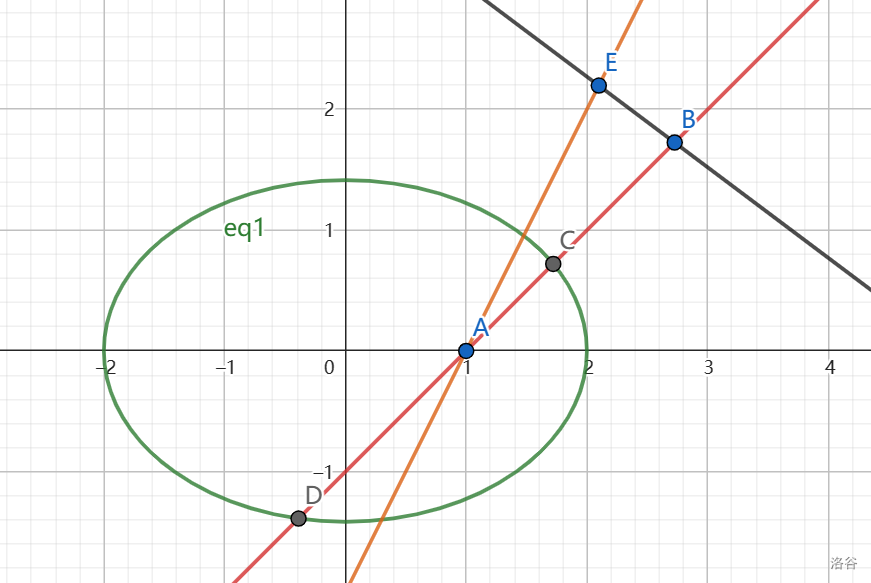
(因为我懒了所以这个图不是按照极点极限的结论的比例做的图，会意即可)

他描述的是对于椭圆内一点 A 做一条线与椭圆交于两点 C,D，作一点 B 使得 A,B,C,D 四个点构成调和点列，翻译：\(|AC||BD|=|CD||AB|\)，B 在定直线上，或许看起来没什么大用？

另一种引入的方式是我们知道对于椭圆外一点 \((x_0,y_0)\) 做椭圆的两条切线两个切点连成的直线叫切点弦，而切点弦的公式也是众所周知的 \(\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1\)，那么对于椭圆上一点套用这个公式会得到的显然是该点的切线方程，那么我们会自然一点也不自然思考如果该点在椭圆内会发生什么？

既然我写在这里那想必肯定是对应的极线了，也就是第一种引入中所过的定直线。

TAOC(The Acumulation Of Conic)

对于韦达定理的优化方案

打个比方，对于一个比较常见的现象，两条直线的斜率相加，这个东西显然可以使用之前说过的齐次化来解决，但是有的时候就有点大材小用了，于是我学到了下面这个神奇的东西，先写，然后再进行解释。

过 \((-2,0)\) 的与两点 \((x_1,y_1)\),\((x_2,y_2)\) 的连线的斜率之和显然可以写成：

\[k_1+k_2=\frac{y_1}{x_1+2}+\frac{y_2}{x_2+2} \]

化简得到：

\[k_1+k_2=\frac{y_1x_2+y_2x_1+2(y_1+y_2)}{(x_1+2)(x_2+2)} \]

这个时候我们发现好像算不了，韦达定理没法针对这种 \(xy\) 交叉出现的情况，怎么办呢？我们不妨退回到刚才那步，注意到这两个点不可能是凭空出现的，一般来说都是有约束条件的，而最简单的为非就是一条直线与圆锥曲线的两个交点，那么我们就可以设这条直线的方程为 \(y=kx+m\),下面是最重要的一步——将方程带入化简之前的柿子！

\[k_1+k_2=\frac{kx_1+m}{x_1+2}+\frac{kx_2+m}{x_2+2} \]

\[k_1+k_2=k+\frac{m-2k}{x_1+2}+\frac{m-2k}{x_2+2} \]

\[k_1+k_2=k+\frac{(m-2k)(x_1+x_2)+4(m-2k)}{x_1x_2+2(x_1+x_2)+4} \]

这不就解决了？关键的关键，在于金手指把 y 替换成 x 是能够和分母约掉一些并且合并成较为好看的结构。

神秘的抛物线性质

对于一条任意的与抛物线有两个交点的直线，两个交点分别是 \((x_1,y_1)\) 和 \((x_2,y_2)\)，容易发现直线的斜率就是 \(\frac{y_2-y_1}{x_2-x_1}\)，和抛物线方程 \(y^2=2px\) 联立得到 \(\frac{y_2-y_1}{\frac{y_2^2}{2p}-\frac{y_1^2}{2p}}=\frac{2p}{y_1+y_2}=\frac{p}{y_中}\)。

设这条直线方程为 \(x=my+t\) 与 \(y^2=2px\) 联立得，\(y^2-2pmx-2pt=0\)。

\[y_1y_2=-2pt \]

\[t=-\frac{y_1y_2}{2p} \]

甚至还有更加神秘的性质：

这里等待补全。

阿基米德三角形

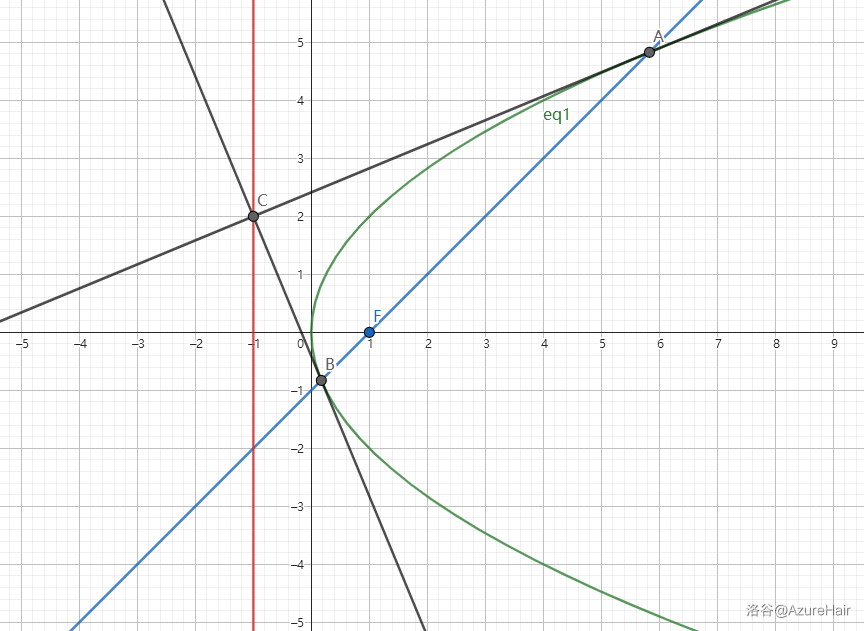
先简述一下，过焦点的直线与抛物线交于两点，这两点做抛物线的切线交于一点，则这个点在定直线 \(x=-1\) 上。

熟悉极点极线的同学就发炎了，这不就是极点极线吗？

(确实就是

简单证明一下他的推广：

设直线 \(x=my+t\) 与 \(y^2=2px\) 交于两点 \(A,B\)。

\[y^2-2pmy-2pt=0 \]

根据留一半大法，\(x_0,y_0\) 处的切线方程就是：\(y_0y=px+px_0\)，然后我们将两点带入小小联立一下得到：

\[\frac{px+px_1}{y_1}=\frac{px+px_2}{y_2} \]

\[p\times \frac{y_2-y_1}{y_1y_2}x=\frac{}{y_1y_2} \]

摆摆摆摆摆，考完期末再写。

导数启动启动启动！期末考试rp++