反向传播

B站视频学习链接：3 反向传播

目录

0 复习回顾

在上一节课程中，主要使用的是numpy库函数配合梯度下降算法来进行咱们权重的一个选取操作。

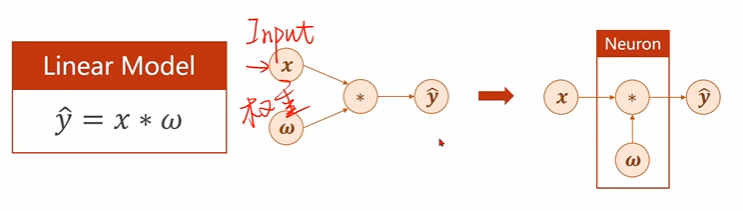
主要的模型是一个最简单的线性模型(是线性模型里面最简单的一个哈)，\(\hat{y}=x*\omega\)，用这个模型进行的一个算法的模拟。就像是下面这个图片展示的这个样子。

第一步、咱们输入了变量\(x\)和相对应的权重\(w\)，并将这两个变量按照函数要求进行数值相乘，得到咱们的计算值\(\hat{y}\)。

第二步、将得到的计算值\(\hat{y}\)作为输入重新进入下一层内求出损失函数\(loss\)。

image-20250828141240269

第三步、求解该损失函数在该条件下的梯度，\(\frac{\partial loss_n}{\partial\omega}=2\cdot x_n\cdot(x_n\cdot\omega-y_n)\)。

第四步、重新更新咱们的权重，\(\omega=\omega-\alpha\frac{\partial loss}{\partial\omega}\)，知道稳定收敛为止。

image-20250828141347184

咱们上一次的例子是一个线性的模型，同时还是线性模型里面最简单的一个模型，因此在计算解析式的时候难度不大，但是一般而言，咱们的深度学习网络是有很多层的，并且输入的变量个数也不仅仅只有一个，像是下面这图片所示。

试问这种类型的深度学习网络模型该如何求解他的解析式呢？

这个模型左侧有\(5\)组\(x\)的输入，第一个隐层有\(6\)个节点，因此第一层就有\(30\)个权重，那么后面慢慢累积起来，这个运算量大的恐怖，基本上是无法求解他的解析式的！

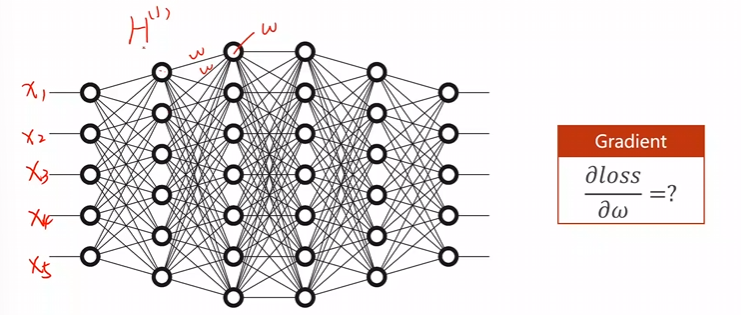
image-20250828141440063

那么我们应该如何求解他的梯度呢，这个时候咱们想到了链式法则。

1 反向传播原理

1.1 引入原理

首先让我们上一点难度，看看双层的线性模型是个什么样子的，下面是一个双层的神经网络模型\(\hat{y}=W_{2}(W_{1}\cdot X+b_{1})+b_{2}\)。

image-20250828141859910

这个是一个双层的神经网络，首先咱们看看他的第一层，也就是权重\(w_1\)所在的那一层

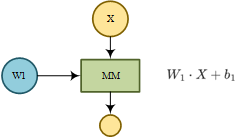
image-20250829221621340

在这里面我们令\(H^{(1)}\)作为我们的隐层则有\(H^{(1)} = W_1^{T}X\)。这几个数据的形状为

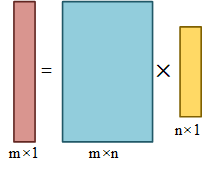
image-20250829222722186

因此第一层是这个玩意儿，我们需要确定矩阵的形状大小，一定要求这\(W_1\)的大小是\(m \times n\)的其中\(mm\)表示的是\(matrix multiplication\) 每一个隐层都有一个偏置量即\(bias-b\)，\(b_1\)是\(m\)维度的

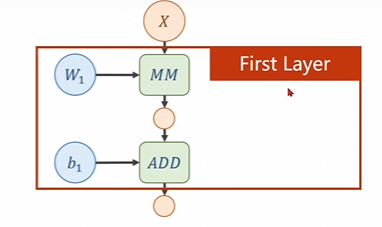
image-20250829161729428

然后我们将第一层的输出结果进行再一次的矩阵乘法，便得到了第二层的神经网络。

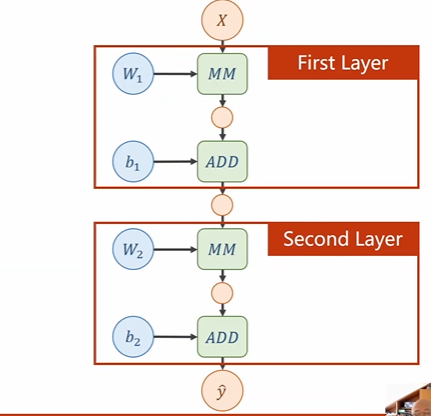
image-20250829161806892

而对于矩阵求导的话可以找一本书叫做\(mairix\ cookbook\)这本书

本地位置： [martix cookbook.pdf](....\martix cookbook.pdf)
网络连接：martix-cookbook-pdf

j如果咱们现在将上面讲的双层线性模型进行展开可以得到下面这个东西，不难看出多层线性变换可以获得同一个形式的解，因此这么多层就没有意义了，故需要添加非线性的层才有意义。

\[\begin{aligned}&\hat{y}=W_{2}(W_{1}\cdot X+b_{1})+b_{2}\\&=W_{2}\cdot W_{1}\cdot X+(W_{2}b_{1}+b_{2})\\&=W\cdot X+b\end{aligned} \]

就像下面一样我们可以适当的引入一些非线性层会更加的有意义。

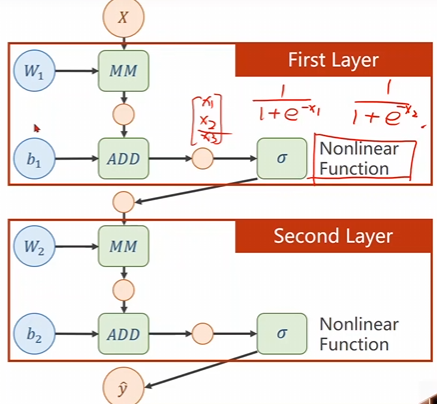
image-20250829162319156

上面就是采用了一些非线性的函数进行了优化以防止展开成基本相同的线性函数。

1.3 求导法则

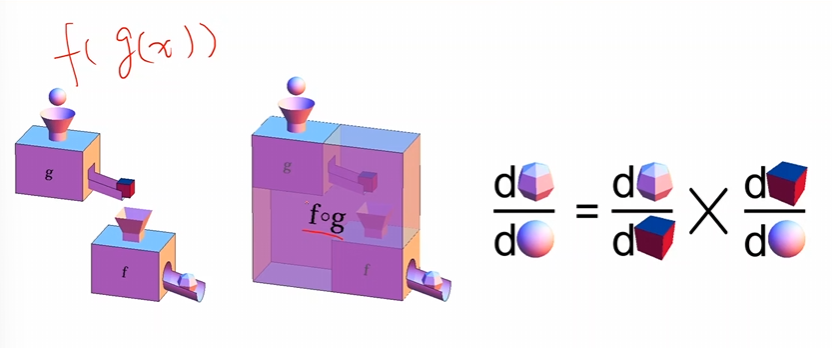
image-20250829162557375

上面是一个比较好的一个概念，其中\(g , f\)这两个分别是两种对应法则，\(fog(x)\)就是\(f(g(x))\)因此，如果相对x求导数，那么就需要使用矩阵的链式法则。

\(\frac{\mathrm{d}fog(x)}{\mathrm{d}x}=\frac{\mathrm{d}fog(x)}{\mathrm{d}g(x)}\times\frac{\mathrm{d}g(x)}{\mathrm{d}x}\)

最主要的就是这个链式法则在矩阵上面的应用。

1.4 求导计算图

现在咱们同样对一个最简单的模型\(\hat{y}=x\times \omega\)进行讲解。

前馈；输入参数\(x,w\)我们将这两个参数传入到模型\(f(x)\)中，便可以得到第一个函数\(z= f(x,w)\)，这个时候的\(z\)实际上就是所谓的虚拟计算值，将这个数值和真实值一起边可求得损失函数\(loss()\)，有了损失函数便可以使用梯度下降算法进行权重的求解啦。

反馈(反向传播)；反向和正向在说法上就刚好相反，首先我们得到了损失函数关于传入参数\(z\)的导数\(\frac{\partial z}{\partial \omega}\)这时候我们拟用链式求导法则，通过\(\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\cdot\frac{\partial z}{\partial x}\)求得\(z\)对\(x\)的导数；通过\(\frac{\partial L}{\partial\omega}=\frac{\partial L}{\partial z}\cdot\frac{\partial z}{\partial\omega}\)求得\(z\)对\(\omega\)的导数。

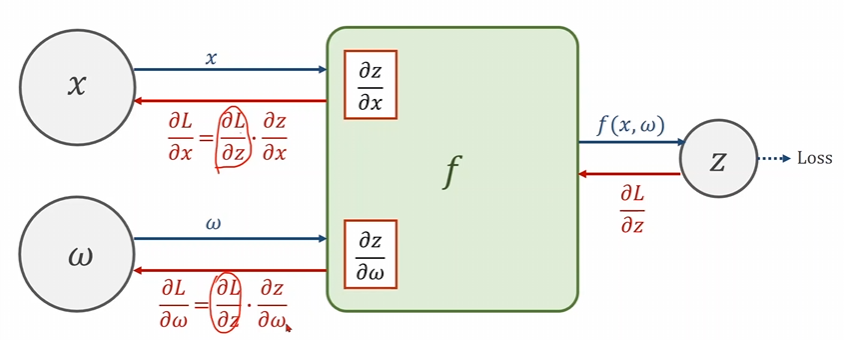
image-20250829163257883

这就是一个最简单的求导计算图。黑色箭头就是最简单的从前面到后面的一个前馈，而红色箭头便是反向传播。

举一个例子吧。

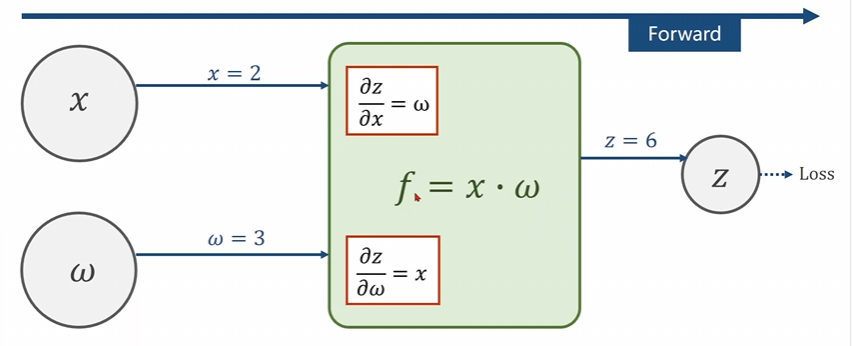
image-20250829163327331

上面就是一个正向的前馈处理。

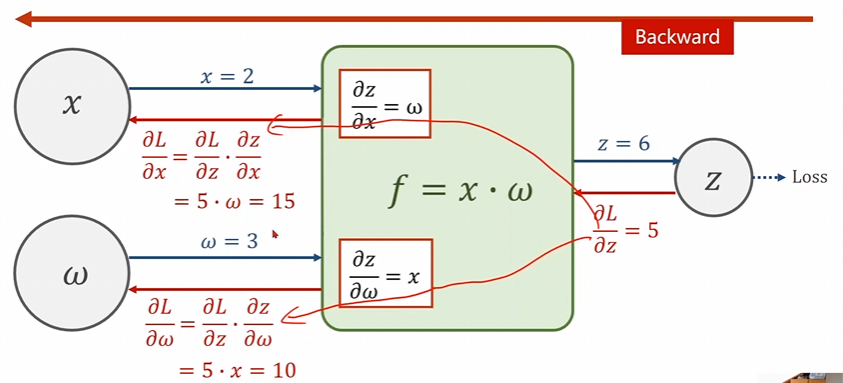
image-20250829163536505

这个是反向传播，首先在进行前面的传播过程我们可以得到\(l\)对\(z\)的导数是\(5\)然后反向及逆行。这个样子就可以求出相应的\(w\)了。注意哈l对\(z\)的偏导是给出的。

现在给出一个具体的模型来处理尝试

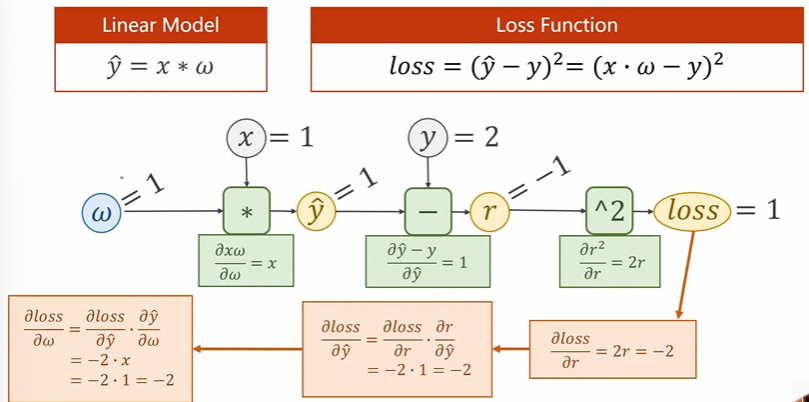
image-20250829164150723

先进行前向处理，后进行反向传播之后便可以得到解答。

2 代码使用

2.1 分块编写

咱们使用的是pytorch进行编写哈。其中的所有的数据均是在一个叫做Tensor的东西。然后我们又开了两个玩意儿一个是他的数据\(data\)也即是权重，另一个是\(grad\)也就是所谓的梯度也即是损失函数对权重的导数。这两个就是最重要的两个参数。

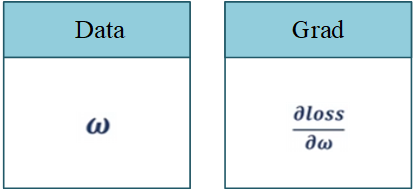
image-20250829223830943

因此对于一个普通的最简单的线性模型\(\hat{y}=x\times \omega\)而言他的计算图绘制如下所示。

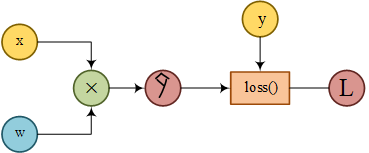
image-20250829225912780

在进行代码编写的时候最重要的就是整出这样子的计算图。

现在让我们正式开始代码的编写。

首先引入库，同时定义训练数据，并初始化权重，同时开启自动保存梯度的开关。

import torch # 引入库

x_data = [1.0, 2.0, 3.0] #给定训练数据
y_data = [2.0, 4.0, 6.0]

w = torch.Tensor([1.0]) # 初始化权重
w.requires_grad = True # 开启自动保存梯度的开关

image-20250829164823859

注意：w.requires_grad = True这个表示的是需要进行梯度的计算,并开启自动保存。

然后咱么开始各个函数的配置。

首先就是前馈相乘函数forward()

其次就是计算损失的损失函数loss()

def forward(x): #前馈相乘函数
    return x * w

def loss(x, y): # 计算损失的损失函数
    y_pred = forward(x)
    return (y_pred - y) ** 2

image-20250829213540998

image-20250829213706377

注意：\(x\)和\(w\)是一个数乘，但是\(x\)并不是一个\(tensor\)需要将\(x\)转换成\(tensor\)即可。

现在就可以进行深度学习求解权重的处理了。

这里给一个以循环轮数为循环变量，同时循环的最大轮数为100轮；

其次读取咱们的训练数据；

开始进行计算图的前馈模拟；

前馈完毕后进行反向传播backward()

然后重新更新这个权重，

更新好之后将权重里面的梯度数据进行一个清理操作即可。

print("predict (before training)", 4, forward(4).item())

for epoch in range(100): #以循环轮数为循环变量，同时循环的最大轮数为100轮
    for x, y in zip(x_data, y_data): #读取咱们的训练数据
        l = loss(x, y) #计算图的前馈模拟
        l.backward() #进行反向传播
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data #重新更新这个权重
        
        w.grad.data.zero_() #将权重里面的梯度数据进行一个清理
        
	print("progress:", epoch, l.item())
print("predict (after training)", 4, forward(4).item())

image-20250829213921513

image-20250829213952830

注意：backward())这个函数用来反向传播并且计算路上的每一个梯度，同时将这个求出来的梯度存储在w里面。

但是一旦进行backward之后loss便被释放了，这个计算图就没了。

image-20250829214132202

注意：获取梯度的数据方法，注意这个grad也是一个tensor，一定要用data进行计算，要不然的话会整出一个新的计算图了。
item是将梯度的数值直接拿出来变成一个标量。防止产生计算图。
权重的更新一定要使用data而非直接用张量计算。防止出现计算图。

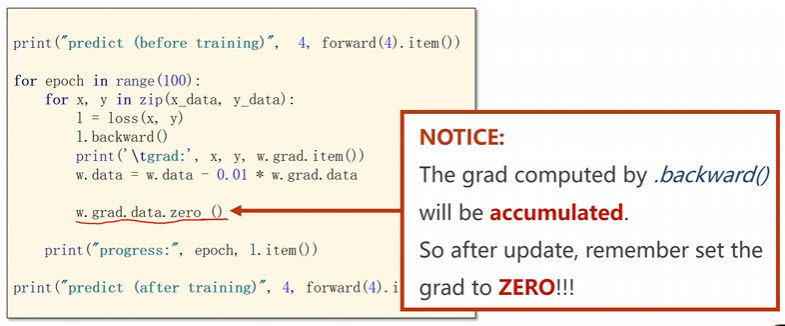
image-20250829214540316

注意：将权重里面的梯度数据全部进行一个清零操作。否则在下一轮的时候上一轮的梯度数据会进行一个重合操纵，这样就出问题了。

这就是使用pytorch来进行反向传播的操作。

2.2 代码综合

  1. 简单的线性模型的使用
import torch
import numpy as np # 引入库函数
import matplotlib.pyplot as plt
import time

x_data=[1.0 ,2.0 , 3.0 , 4.0 , 5.0]
y_data=[2.0 , 4.0 , 6.0 ,8.0 , 10.0]

w = torch.tensor([1.0])
w.requires_grad = True

def forward(x):
    return x*w

def loss(x,y):
    y_hat= forward(x)
    return (y_hat-y)**2

MSE_list = []
epoch_list = []

plt.ion()
fig,ax = plt.subplots(figsize = (10,6)) # 创建图表对象和坐标轴对象

plt.pause(10)

for epoch in range(0 , 16 , 1): # 轮数为15轮
    for x,y in zip(x_data , y_data):
        l =loss(x ,y)
        l.backward() # 反向传播
        w.data = w.data - 0.01 * w.grad.data

        w.grad.data.zero_()
    print("progress:", epoch, l.item())
    MSE_list.append(l.item())
    epoch_list.append(epoch)

    # 更新图表
    ax.clear()
    ax.plot(epoch_list , MSE_list , 'b-o' , linewidth = 2 , markersize = 4)
    ax.set_xlabel('epoch' ,fontsize = 12)
    ax.set_ylabel('MSE loss' , fontsize = 12)
    ax.set_title(f'Training progress (Epoch{epoch})' , fontsize = 14)
    ax.grid(True , alpha = 0.3)
    ax.text(
        0.02 , 0.95, # x坐标和y坐标
        f'Current W:{w.item():.4f}',#显示当前的权重值，并保留四位小数
        transform = ax.transAxes, #使用坐标轴相对坐标
        fontsize = 10,  #字体大小
        bbox = dict(
            boxstyle="round,pad=0.3", #圆角矩形框,内边距
            facecolor = "yellow", #背景颜色
            alpha = 0.7 #透明度
            )
    )
    plt.pause(0.5) #每一轮后暂停0.5秒

plt.ioff()
plt.show()


print("predict (after training)", 4, forward(4).item())

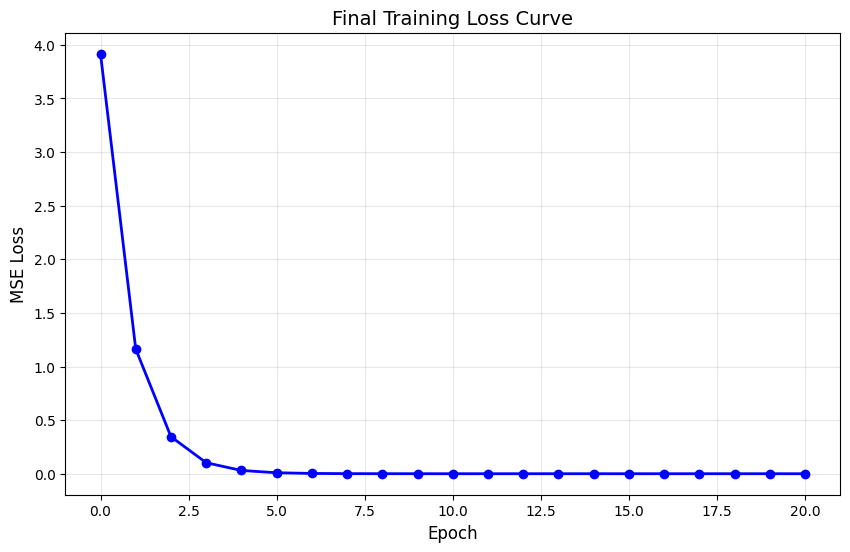
# 最终绘制完整的损失曲线
plt.figure(figsize=(10, 6))
plt.plot(epoch_list, MSE_list, 'b-o', linewidth=2, markersize=6)
plt.xlabel('Epoch', fontsize=12)
plt.ylabel('MSE Loss', fontsize=12)
plt.title('Final Training Loss Curve', fontsize=14)
plt.grid(True, alpha=0.3)
plt.show()

ezgif.com-animated-gif-maker (1)

img

3 课后作业

3.1 换一组变量进行推导并绘制其计算图

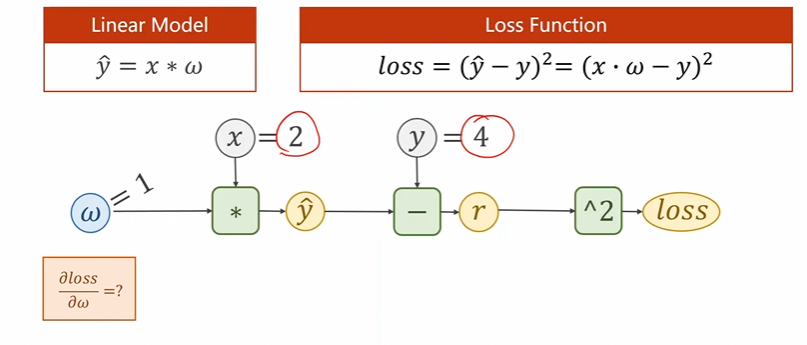
​ image-20250829164407921

现在给出这个题目的解答。

1. 正向传播（前馈）

\(\begin{aligned}&\text{正向传播(前馈).}\\&①\text{输入 }x=2;\quad w=1(\text{初步估计值}).\\&②\hat{y}:x\cdot w=2\times1=2.\\&②r=\hat{y}-y=2-4=-2\\&④loss=r^2=4.\end{aligned}\)

2. 反向传播

\(\begin{aligned}&\text{反向传播}\\&①\text{ 已知 }loss=r^2,\quad\Rightarrow\quad\frac{\partial loss}{\partial r}=\frac{\partial r^2}{\partial r}=2r=-4\\&②\text{ 求 }\frac{\partial loss}{\partial\hat{y}}=\frac{\partial loss}{\partial r}\times\frac{\partial r}{\partial\hat{y}}=2r\times\frac{\partial(\hat{y}-y)}{\partial\hat{y}}=2r=-4\\&②\text{ 求 }\frac{\partial loss}{\partial w}=\frac{\partial loss}{\partial\hat{y}}\times\frac{\partial\hat{y}}{\partial w}=2r\times\frac{\partial(x\cdot w)}{\partial w}=2rx=-8\end{aligned}\)

3. 计算图的绘制

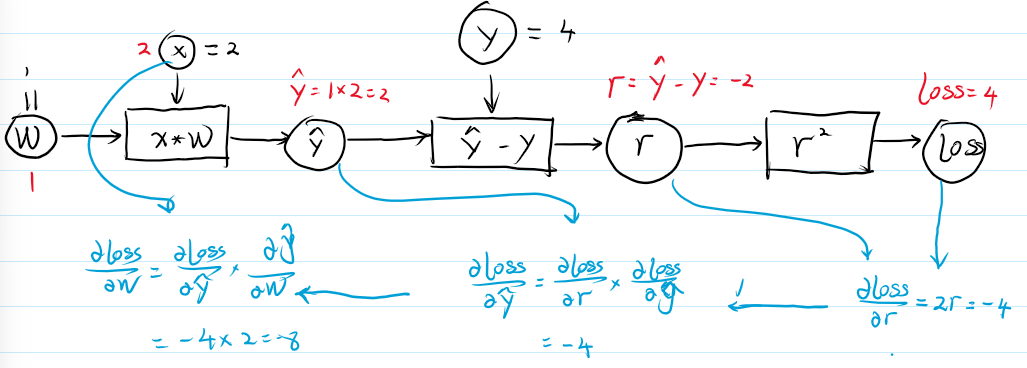
image-20250830101029515

3.2 增加模型复杂度继续进行pytorch求解

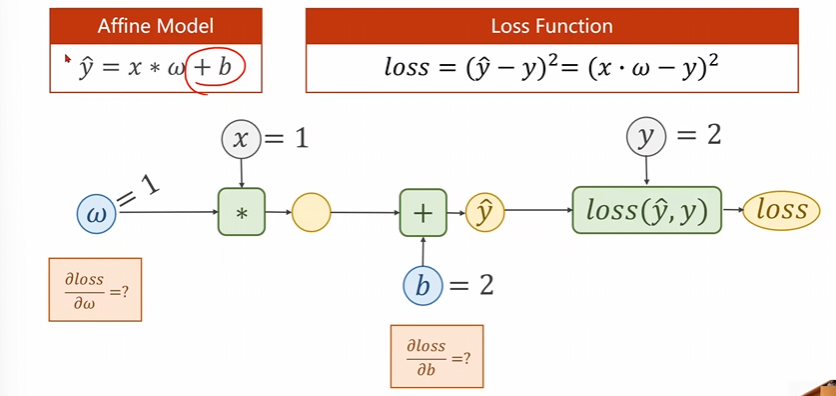
​ image-20250829164440947

现在给出这个题目的解答

  1. 正向传播

\[\begin{aligned}&\text{正向传播(前馈)}\\&①\text{输入}:x=1,w=1,\Rightarrow x\cdot w=1.\\&②\text{输入}:b(\text{偏置})=2\Rightarrow\hat{y}:x\cdot w+b=3.\\&②\text{输入}:y=2\Rightarrow r=\hat{y}-y=1.\\&④\text{ 输入}:r=1\Rightarrow loss=r^2=1\end{aligned} \]

  1. 反向传播

\(\begin{aligned}&\text{反向传播}\\&①\frac{\partial loss}{\partial r}=\frac{\partial r^2}{\partial r}=2r|r=1=2.\\&②\frac{\partial loss}{\partial y}=\frac{\partial loss}{\partial r}\cdot\frac{\partial r}{\partial y}=2r\times\frac{\partial(\hat{y}-y)}{\partial\hat{y}}=2r=2\\&③\frac{\partial loss}{\partial z}=\frac{\partial loss}{\partial y}\times\frac{\partial g}{\partial z}=2r\times\frac{\partial(z+b)}{\partial z}=2r=2\\&④\frac{\partial loss}{\partial w}=\frac{\partial loss}{\partial z}\times\frac{\partial z}{\partial w}=2r\times\frac{\partial(x\cdot w)}{\partial w}=2rx=2\end{aligned}\)

  1. 计算图绘制

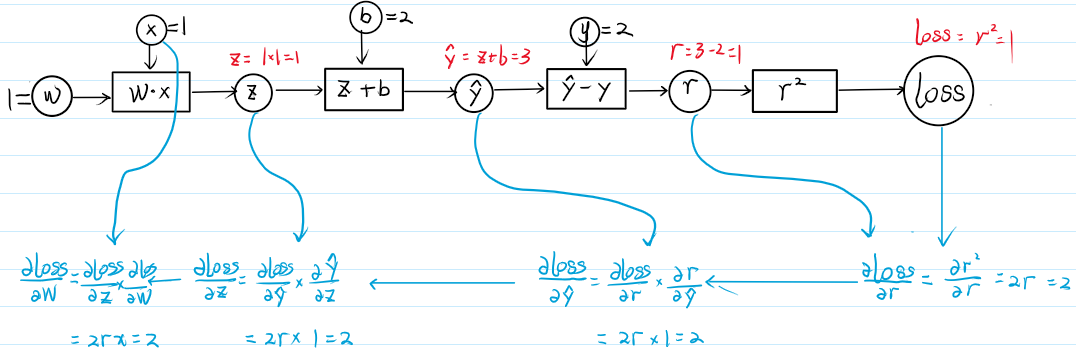
image-20250830103237282

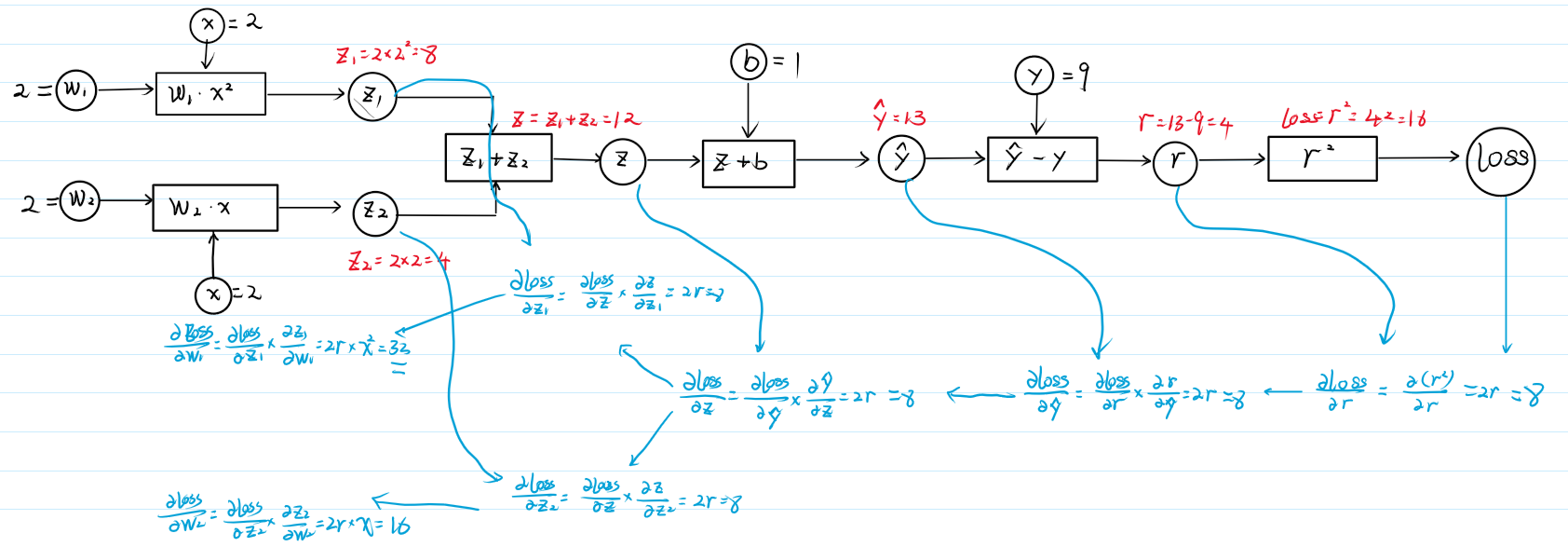
3.3 尝试使用二次函数模型进行反向传播的求解

image-20250829214924771

现在给出这个题目的解答

  1. 正向传播

① 输入: \(w_1=2\), \(x=2\) \(\Rightarrow\) \(z_1=w_1 \times x^2=2 \times 4=8\).

② 输入: \(w_2=2\), \(x=2\) \(\Rightarrow\) \(z_2=w_2 \times x=2 \times 2=4\).

③ 输入: \(z_1\), \(z_2\), \(\Rightarrow\) \(z=z_1+z_2=8+4=12\).

④ 输入: \(z\), \(b\). \(\Rightarrow\) \(\hat{y}=z+b=13\)

⑤ 输入: \(y\) \(\Rightarrow\) \(r=\hat{y}-y=13-9=4\)

⑥ 输入: \(r\) \(\Rightarrow\) \(loss=r^2=16\).

  1. 反向传播

① \(\frac{\partial loss}{\partial r} = \frac{\partial (r^2)}{\partial r} = 2r |_{r=4} = 2 \times 4 = 8\)

② \(\frac{\partial loss}{\partial z} = \frac{\partial loss}{\partial r} \times \frac{\partial r}{\partial z} = 2r \times \frac{\partial (z+b)}{\partial z} = 2r = 8\)

③ \(\frac{\partial loss}{\partial z_1} = \frac{\partial loss}{\partial z} \times \frac{\partial z}{\partial z_1} = 2r \times \frac{\partial (z_1 + z_2)}{\partial z_1} = 2r = 8\)

④ \(\frac{\partial loss}{\partial z_2} = \frac{\partial loss}{\partial z} \times \frac{\partial z}{\partial z_2} = 2r \times \frac{\partial (z_1 + z_2)}{\partial z_2} = 2r = 8\)

⑤ \(\frac{\partial loss}{\partial w_1} = \frac{\partial loss}{\partial z_1} \times \frac{\partial z_1}{\partial w_1} = 2r \times \frac{\partial (w_1 \cdot x^2)}{\partial w_1} = 2r \times 4 = 32\)

⑥ \(\frac{\partial loss}{\partial w_2} = \frac{\partial loss}{\partial z_2} \times \frac{\partial z_2}{\partial w_2} = 2r \times \frac{\partial (w_2 \cdot x)}{\partial w_2} = 2r \times 2 = 16\)

  1. 计算图的绘制

image-20250830111154436

posted @ 2025-08-29 23:19  AxonoSensei  阅读(22)  评论(0)    收藏  举报