6 线性回归算法

0 引言
1 线性回归算法
2 线性回归算法代码实现
- 2.1 从零开始搭建
- 2.2 简洁实现

[!IMPORTANT]

B站视频链接 6 线性回归算法

0 引言

这个线性回归算法没啥好说的，作为深度学习入门的第一个算法，也是后面算法的基础，认真学习便是。

本文包括了深度学习算法的数学模型和代码的实现。

在数学方面，我们需要预先学习好线性代数以及微积分的相关知识才可以进行学习。注意本文的符号主要有下面三种，各个不同。

\[\begin{align} &1. 小写字母 a、b 、c 表示数据也可以说是标量\\ &2.带有箭头的字母\vec{a}、\vec{b}、\vec{c}之类的表示向量、也就是好多个标量，同时默认为列向量。\\ &3.大写字母A、B、C表示矩阵 \end{align} \]

而在代码方面，使用本文说到的各种代码的时候一定要预先下载并配置好环境，要求可以正确引用下面这几个库函数。

import torch
import numpy as np
import matplotlib.pyplot as plt
from d2l import torch as d2l

确认准备完毕之后便可开始线性回归算法的学习和说明了。

1 线性回归算法

1.1 引例

首先我们用一个比较简单的例子来引入线性回归的算法，那就是贯彻中国人一生的买房问题。

现在一套房子的价格达到了上百万甚至是上千万，对于一个正常的普通百姓工人阶级而言，这样一套房子可以说是一辈子才能支付的起的大件物品，因此在购买房子的时候我们希望买的房子价格尽可能的低一些，哪怕少一万元都是好的，这个时候我们就需要对一个地区的房子价格进行预测，并找到在那个地方，什么时候买是比较划算的。

从上面的文字中可以看出，一套房子的价格和很多很多的因素有关。譬如下面几个因素。

购买时间，1999年和2025年的房子价格肯定是完全不一样。
房子位置，撒哈拉沙漠的房子怎么样都没有北京的房子贵。
房子大小，一套6平方米的房子和600平方米的别墅这两个的价格，也不用说了吧。
人文因素，一个房子里面如果有过凶杀案等问题，房子的价格基本崩盘了
自然因素，如果一个地方经常火山爆发、山洪海啸等那房价应该也不会特别高。

那么我们难道直接将上面的因素转化成硬性指标直接相加吗？显然不是。各个因素之间的影响比重肯定是不一样的呀！

举个简单的例子，现在有两个房子，其中一个房子大小是10平方米、但是位于北京的学区；另一套房子的大小是100平方米、但是位于沙漠里面。这两个房子我想用脑子一想就知道肯定是北京的房子贵，哪怕它的面积小了一些。这个时候不难看出，地区好像比大小更加的重要欸。

这个重要二字便恰如其分的表现了这两个因素之间的比重问题。故此我们需要采用不同的比重来对每个因素的影响情况进行调整，从而得到一个完美的元素比重，确定最终的函数关系。

这个过程就是线性回归算法的基本过程。

1.2 数学的简单实现

好那么有了上面的引例，便可用数学的语言进行解释了。现在我们先考虑一个影响因素购买时间，来简单的说明一下。

首先我们假设某个房子的价格为$\vec{y}$，注意这个$\vec{y}$是一个向量，假设它里面包括了近十年的房子的真正的价格，即，

\[\vec{y} =[y_1,y_2,\cdots ,y_{10}]^T \tag{1-1} \]

同时有影响因素年份$\vec{x}$，注意这个$\vec{x}$也是一个向量，它里面包括了近十年的年份，即，

\[\vec{x} =[x_1,x_2,\cdots ,x_{10}]^T = [2016,2017,\cdots,2025] \tag{1-2} \]

令年份和房子之间的影响权重为$\vec{w}$，注意$\vec{w}$也是一个向量，他里面有各个因素的影响权重，但是这里只有一个影响因素，则

\[\vec{w} = [w_1]^T \tag{1-3} \]

最后我们再给一个偏移量$b$，用来偏移修正的。

综上可以设出我们的虚拟价格表达式子，注意下面这个$\vec {\widehat{y}}$，是我们自己拟合的虚假的房价不是真正的房价！

\[\vec {\widehat{y}} = \vec{w}^T \vec{x}+b \tag{1-4} \]

这个时候我们需要使用这个来计算出怎么样令这个函数的结果$\vec {\widehat{y}}$和真正的结果$\vec{y}$尽可能的接近，因为越接近，说明他的拟合效果最好。

这个时候就需要引入一个评价拟合效果好坏的变量$\vartheta $来定量的确定。

\[\vartheta(y_i , \widehat{y}_i)=\frac{1}{2} (y_i-\widehat{y}_i)^2 \tag{1-5} \]

这个是任意一个房子的评价标准，那么如果有很多的数据呢，用向量的形式书写如下。

\[\vartheta(\vec{y} ,\vec{ \widehat{y}})=\frac{1}{2n} (\vec{y}-\vec{ \widehat{y}})^T (\vec{y}-\vec{ \widehat{y}})= \frac{1}{20} (\vec{y}-\vec{ \widehat{y}})^T (\vec{y}-\vec{ \widehat{y}}) \tag{1-5} \]

这就是单个变量的线性回归方程，拟合后会得到一条直线，用来预测之后的形式。就像是下面这个图片类似

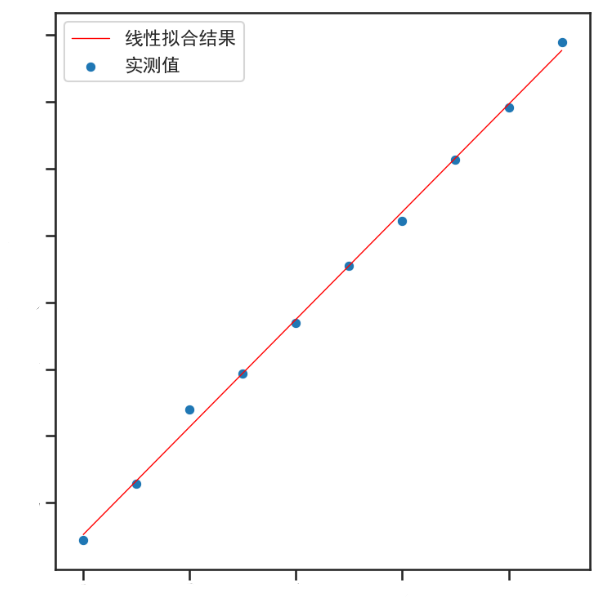
但是实际的情况之下并不仅仅只有这么一个影响因素，而是由很多很多的影响因素，也不仅仅只有这么一个权重，而是很多很多的权重，这个时候便可以将这个模型进行扩展，成为真真正正一般化的线性回归模型。

1.3 数学模型

将上述模型进行扩展

假设真实输出为$\vec{y}$，且有$n$个元素，即

\[\vec{y} = [y_1 , y_2 , y_3 , \cdots , y_n]^T \tag{1-6} \]

虚拟的线性输出为$\vec{\widehat{y}}$，也有$n$个元素，即

\[\vec{\widehat{y}} = [\widehat{y}_1 ,\widehat{y}_2 , \widehat{y}_3 , \cdots , \widehat{y}_n]^T \tag{1-6} \]

假设每一个输出$y_i$都对应一组$\vec{x_i}$，而每一组$\vec{x_i}$了$m$个不同的影响因素$x_{ij}$，即

\[\vec{x_i} = [x_{i1} , x_{i2} , x_{i3}, \cdots , x_{im}]^T \tag{1-7} \]

因为有很多个$y_i$这么多数据样本，则可以得到输入的数据矩阵$X$，是一个矩阵，即

\[X_{n\ \times m}=\left[ \begin{array}{c} \vec{x}_1\\ \vec{x}_2\\ \vdots\\ \vec{x}_n\\ \end{array} \right] =\left[ \begin{matrix}{} x_{11}& x_{12}& \cdots& x_{1m}\\ x_{21}& x_{22}& \cdots& x_{2m}\\ \vdots& \vdots& \vdots& \vdots\\ x_{n1}& x_{n2}& \cdots& x_{nm}\\ \end{matrix} \right] \tag{1-8} \]

同时每一个影响因素$x_{ij}$都对应了一个相应的权重$w_j$，因此有$m$个不同的权重，即

\[\vec{w}=[w_1 , w_2 , w_3 , \cdots , w_m]^T \tag{1-9} \]

最后给出偏移量$b$，那么便可以建立一个相对应的数学线性模型，我们设自己的线性模型的输出为$\vec{\widehat{y}}$，则

\[\vec{\widehat{y}}=\left[ \begin{array}{c} \widehat{y}_1\\ \widehat{y}_2\\ \vdots\\ \widehat{y}_n\\ \end{array} \right] =\left[ \begin{array}{c} x_{11}\times w_1+x_{12}\times w_2+\cdots +x_{1m}\times w_m+b\\ x_{21}\times w_1+x_{22}\times w_2+\cdots +x_{2m}\times w_m+b\\ \vdots\\ x_{n1}\times w_1+x_{n2}\times w_2+\cdots +x_{nm}\times w_m+b\\ \end{array} \right] \tag{1-10} \]

这个时候我们思考一下怎么样将这个矩阵进行化简，不难看出可以这样子做。

首先令$X=\left[ X,1 \right] ,W=\left[ \begin{array}{c} \vec{w}\\ b\\ \end{array} \right]$，此时上述公式可以化为。

\[\vec{\widehat{y}} = XW \tag{1-11} \]

则此时可以给出评价公式为，

\[\vartheta = \frac{1}{2n} \times ||\vec{\widehat{y}}-\vec{y}||^2 \tag{1-12} \]

该公式是可以给出显示解的现在进行推导。

首先将公式进行适当化简展开

\[\begin{align} \vartheta &=\frac{1}{2n}\times ||\vec{\widehat{y}}-\vec{y}||^2 \\ &=\frac{1}{2n}\times(\vec{\widehat{y}}-\vec{y})^T(\vec{\widehat{y}}-\vec{y}) \\ &=\frac{1}{2n}\times(XW-\vec{y})^T(XW-\vec{y}) \\ &=\frac{1}{2n}\times(W^TX^T-\vec{y}^T)(XW-\vec{y}) \\ &=\frac{1}{2n}\times(W^TX^TXW-W^TX^T\vec{y} - \vec{y}^TXW +\vec{y}^T\vec{y}) \\ &=\frac{1}{2n}\times(W^TX^TXW- 2\vec{y}^TXW +\vec{y}^T\vec{y}) \end{align} \tag{1-13} \]

对其求偏导有，

\[\begin{align} \frac{\partial \vartheta}{ \partial W} &= \frac{\partial}{\partial \vec{w}}[\frac{1}{2n}\times(W^TX^TXW- 2\vec{y}^TXW +\vec{y}^T\vec{y})] \\ &=\frac{1}{2n}\times [\frac{\partial}{\partial W}(W^TX^TXW) - \frac{\partial}{\partial W}(2\vec{y}^TXW) +\frac{\partial}{\partial W}(\vec{y}^T\vec{y})] \\ &=\frac{1}{2n}\times[2X^TXW - 2X^T\vec{y}] \\ &=\frac{1}{n}(X^TXW-X^T\vec{y}) \end{align} \tag{1-14} \]

令其为零，则有，

\[\frac{1}{n}(X^TXW-X^T\vec{y}) = 0 \tag{1-15} \]

解得

\[W = [X,1]^{-1}\vec{y} \tag{1-16} \]

至此他的数学模型也就推到完毕了。最终要求的就是一堆权重和偏差罢了。

2 线性回归算法代码实现

2.1 从零开始搭建

import random
import torch
from d2l import torch as d2l
import matplotlib.pyplot as plt

# 搞一个数据集

def synthetic_date(w , b , num_examples):
    X = torch.normal(0 , 1 , (num_examples , len(w))) 
    #均值为0 方差为1的随机数据 num_exapmle是行数，lens是列数
    y =torch.matmul(X , w)+b
    y+=torch.normal(0, 0.01 , y.shape)
    return X , y.reshape((-1,1))
true_w = torch.tensor((2.0,-3.0))
true_b = 4.2
features,labels = synthetic_date(true_w,true_b,1000)

print('features:' , features[0] )
print('label' , labels[0])

# plt.scatter(features[:,1] , labels , s = 5,c = 'b')
# plt.show()

def data_iter(batch_size , features , labels):
    num_examples = len(features)
    indices = list(range(num_examples))#随机读取的
    random.shuffle(indices)#随机打乱下标
    for i in range(0,num_examples , batch_size):
        batch_indices = torch.tensor(
            indices[i:min(i+batch_size,num_examples)]
        )
        yield features[batch_indices] , labels[batch_indices]
        #返回

batch_size = 10
for X,y in data_iter(batch_size,features,labels):
    print(X, '\n' , y)
    break

w = torch.normal(0,0.01 , size = (2,1) , requires_grad=True)
b = torch.zeros(1,requires_grad=True)

# 定义模型
def linreg(X , w , b):

    return torch.matmul(X,w)+b

#定义损失函数
def squared_loss(y_hat , y):
    return(y_hat - y.reshape(y_hat.shape))**2/2


#定义优化算法
def sgd(params , lr , batch_size):
    with torch.no_grad():
        for param in params:
            param-=lr*param.grad / batch_size
            param.grad.zero_()

lr = 0.05
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size,features,labels):
        l = loss(net(X,w,b),y)
        l.sum().backward()
        sgd((w,b),lr,batch_size)
    with torch.no_grad():
        train_1 = loss(net(features,w,b),labels)
        print(f'epoch {epoch+1} , loss{float(train_1.mean()):f}')

print(f'w的估计误差:{true_w-w.reshape(true_w.shape)}')
print(f'b的估计误差:{true_b-b}')

2.2 简洁实现

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
loss = nn.MSELoss()

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

posted @ 2025-08-23 13:35 AxonoSensei 阅读(15) 评论(0) 收藏举报

刷新页面返回顶部

AxonoSensei