5 自动求导

目录

• 0 引言
• 1 向量的链式法则
  • 1.1 情况1
  • 1.2 情况2
  • 1.3 情况3
• 2 链式求导实例
  • 2.1 例1
  • 2.2 例2
• 3 自动求导计算机原理
  • 3.1 计算图原理
  • 3.2 运行模式
• 4 自动求导的代码实现
• 5 finish
  • 5.1 重要函数
  • 5.2 代码全部

[!IMPORTANT]

B站视频链接 5 自动求导

---

0 引言

说个题外话，这个章节好难懂，看了好久也不是特别的理解，究竟在说些什么玩意儿，只能硬着头皮听下去了。

由于在进行深度学习神经网络的计算过程中对求导数这个运算较为重要因此，这里就需要进行实现自动求导这个功能，来帮助进行运算，这个玩意儿应该算是一个基础运算，在深度学习之中。

在使用前我们需要重新复习一下之前求导数的方法，也就是极为知名的链式求导法则。

我们文中提到的全部向量在第一次定义的时候均是列向量，也就是站着的那种向量类型

---

1 向量的链式法则

对于标量而言他的链式求导法则是比较简单明了的，就用下面这个例子表示一下。

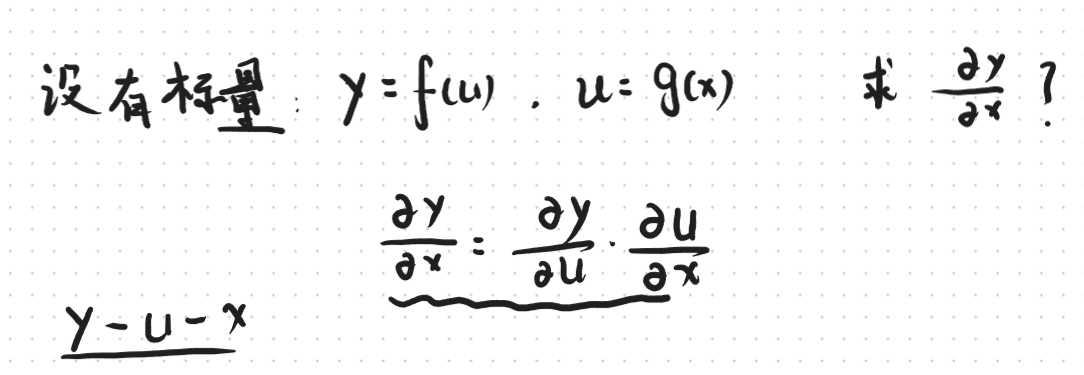
现在我们将标量的链式求导法则扩展到向量进行求解。

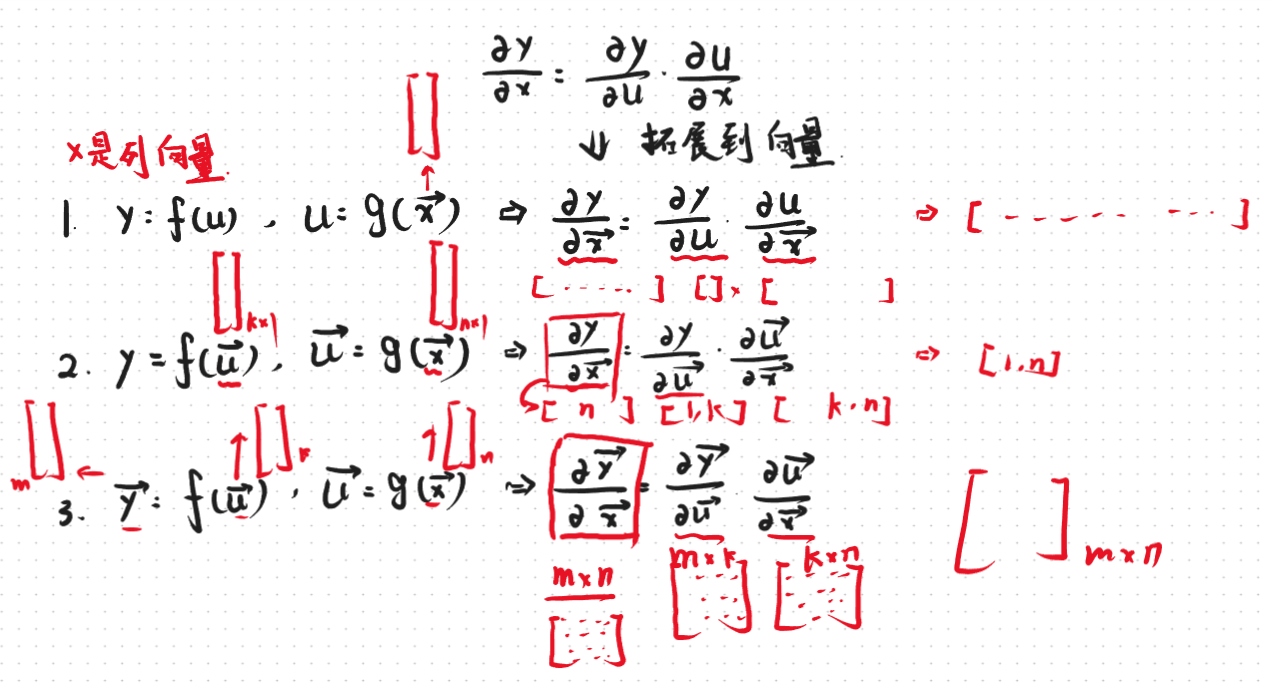
可以看到引入向量之后完全不一样了。

1.1 情况1

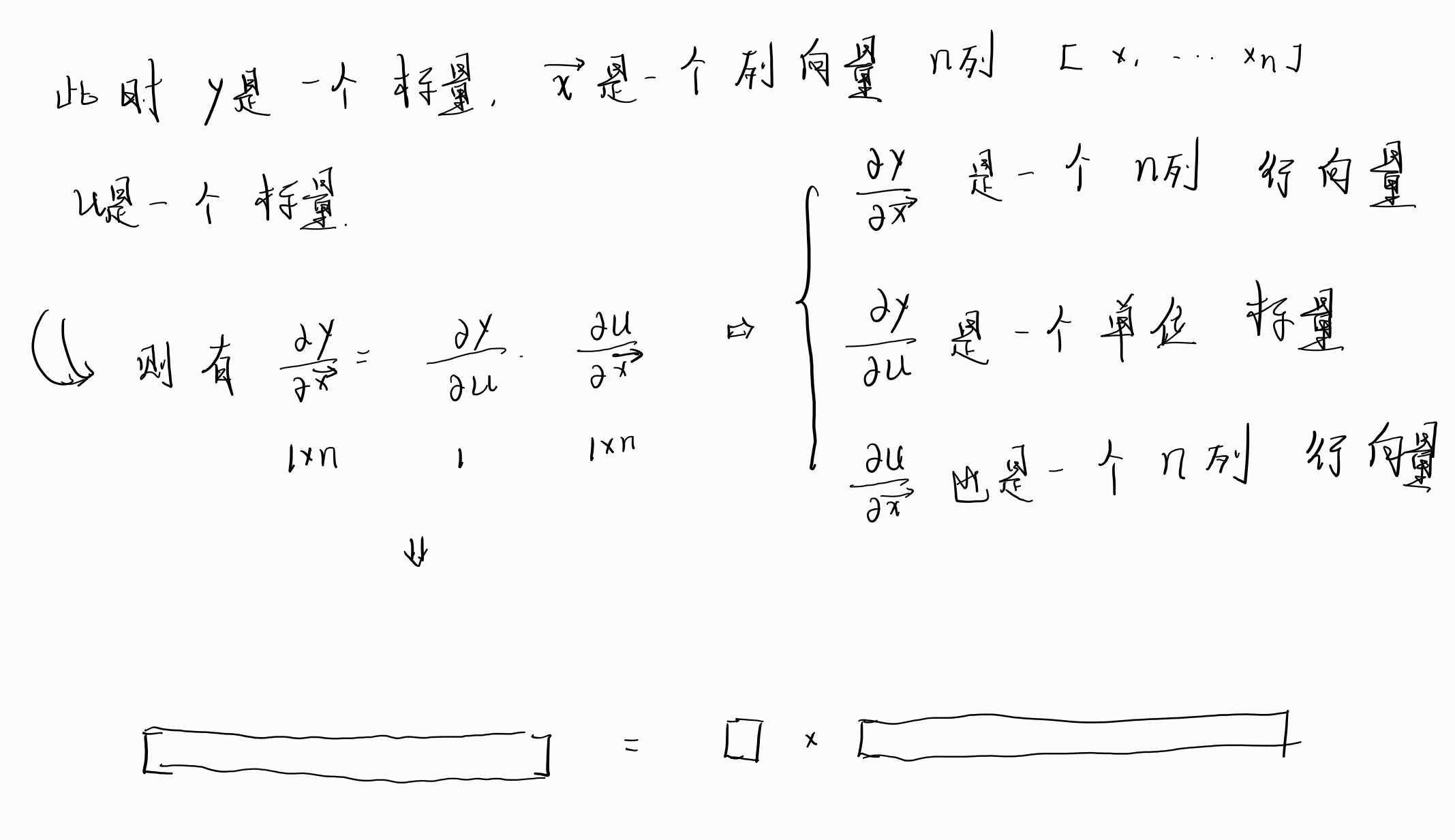
1.2 情况2

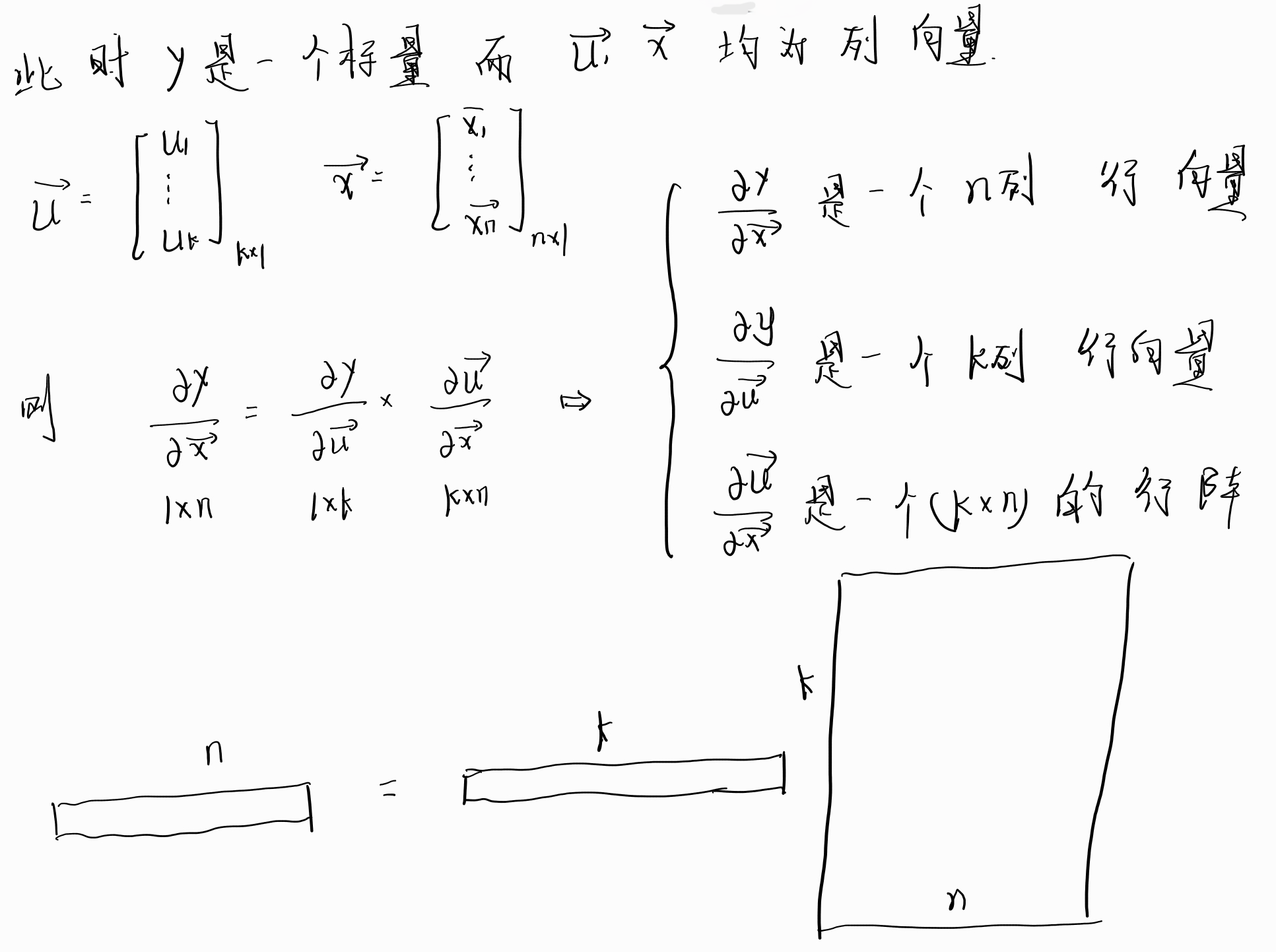
1.3 情况3

上面三种情况从简单到难依次罗列了向量求导过程中的形状和大小，现在对向量的链式求导法则应该是了熟于胸了，那么现在就开始试着采用这个求导法则来真的试试求导的几个例子吧

---

2 链式求导实例

2.1 例1

题目：\(\text{令}\vec{x}和\vec{w}均为n行的列向量,即\vec{x},\vec{w} \in R^n。y是一个标量，即y \in R 。令z = (<\vec{x} , \vec{w}> - y)^2 ，求\frac{\partial z}{\partial \vec{w}}。\)

首先让我们分析一下这个题目，他让我们求导数，因此考虑采用链式求导法则进行求解。注意尖括号里面这两个向量做的是点乘，也就是内积哈。

首先先定义一些中间变量：

\[令： \left\{ \begin{array}{l} a\ =\ <\vec{x},\vec{w}>\\ b\ =\ a-y\\ z\ =\ b^2\\ \end{array} \right. \tag{2-1} \\ \]

则可以将进行链式求导法则得到

\[\begin{align} \frac{\partial z}{\partial \vec{w}} &= \frac{\partial z}{\partial b}\times \frac{\partial b}{\partial a} \times \frac{\partial a}{\partial \vec{x}} \\ &=\frac{\partial b^2}{\partial b}\times \frac{\partial (a-y)}{\partial a}\times \frac{\partial (<\vec{x},\vec{w}>)}{\partial \vec{w}} \\ & = 2b \times 1 \times \vec{x}^T \\ & = 2(a-y)\vec{x}^T \\ &=2(<\vec{x},\vec{w}>-y)\vec{x}^T \end{align} \tag{2-2} \]

2.2 例2

题目：\(令X \in R^{m \times n} , \vec{w} \in R^n , \vec{y} \in R^m , z =||X\vec{w}-y||^2,求\frac{\partial z}{\partial \vec{w}}。\)

首先和前面一样的方法先搞几个中间变量来，将z尽可能的规划的简单一些。

\[令：\left \{\begin{array}{l} a&=X\vec{w} \\ b&=a-\vec{y} \\ z&=||b||^2 \end{array} \right. \tag{2-3} \]

现在就可以采用伟大的链式法则来求解一下这个题目了

\[\begin{align} \frac{\partial z}{\partial \vec{w}} &= \frac{\partial z}{\partial b}\times \frac{\partial b}{\partial a} \times \frac{\partial a}{\partial \vec{x}} \\ &=\frac{\partial ||b||^2}{\partial b}\times \frac{\partial (a-\vec{y})}{\partial a}\times \frac{\partial(X\vec{w})}{\partial \vec{w}} \\ &=2b^T\times 1 \times X \\ &=2(a-\vec{y})^T X \\ & = 2(X\vec{w}-\vec{y})^TX \end{align} \tag{2-4} \]

到这里，这两个举例应该让链式法则求导数这件事情变得比较的清晰了一些，但是我们总不能一直用手来算吧，一直用手算还叫什么自动求导呀！

现在就开始进行计算机的求导方法。

---

3 自动求导计算机原理

3.1 计算图原理

在计算机里面进行求导，其原理和我们手动求导的原理是一样的，也是利用中间变量配合链式法则进行求导，他的求导过程只需要下面两个东西。

1. 计算的代码块也就是操作子。
2. 计算无环图片。

那么我们就拿着例1的题目进行举例说明。

以这个题目为例进行求解的过程主要分成了三个步骤

1. \(\vec{w}和\vec{x}产生中间变量a\) 。
2. \(a和y产生中间变量b\) 。
3. \(b产生应变量z\)

那么我们可以画出他的计算图（无环的）

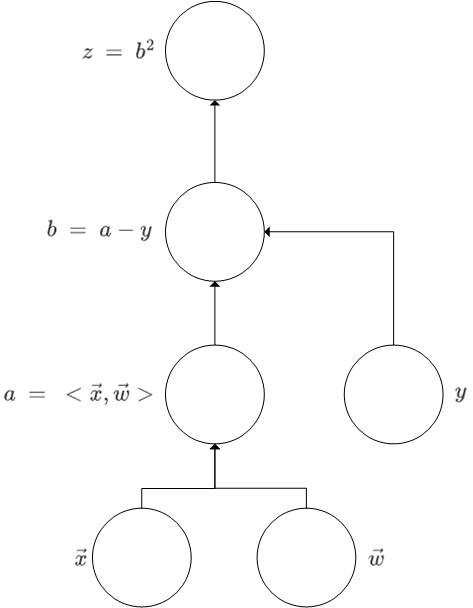
在计算机里面便是如此。

3.2 运行模式

不过在计算机的运行过程中对于求导的模式不仅仅是上面说的一种，实际上主要是两种运行模式。

上文说到的就是其中的一种也就是正向运行模式，另外一种就是反向运行模式也可以称之为反向传递。

正反向的区别也就是咱们思维的区别，一般的链式法则都是由很多的中间变量\(u_i\)组成的那么对于一个任何一个函数都可以像是下面这个样子进行求导：

\[\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u_n} \frac{\partial u_{n}}{\partial u_{n-1}} \frac{\partial u_{n-1}}{\partial u_{n-2}} \cdots \frac{\partial u_{2}}{\partial u_{n1}} \frac{\partial u_{1}}{\partial x} \]

那么对于正向模式而言，它是从后向前的一个求导方法的

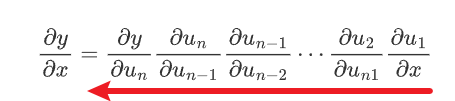
也就是先是对\(x\)然后逐步扩张到\(y\)

而对于反向模式而言，它和正向模式恰好相反，他是从前向后的一个求导方法的

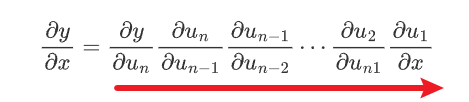
也就是先是对\(y\)然后逐步扩张到\(x\)

下面这个图就十分形象的表现了正向和反向的一个小区别，当然大多数时候咱们主要采用反向进行电脑求解

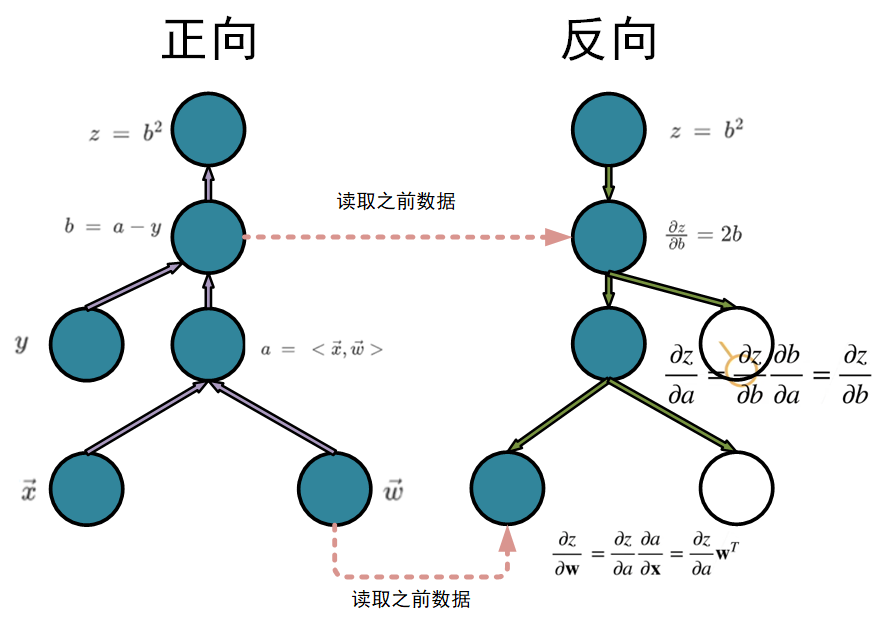
综上所述，正向求导和反向求导最显著的区别就是。

正向求导就是对一个玩意儿猛猛求，只有一个数据，我只存了一个数，不断的对这个数进行更新，最终得到函数。

反向求导就是在求解的过程总会保存曾经的数据，把数都存起来，到时候求什么就取需要的数来用。

好那么到现在这个求解的基本方法是已经搞得差不多了。现在开始对自动求导进行计算机上的演示。

---

4 自动求导的代码实现

首先需要说明一下在进行代码实现之前我们在计算机里面需要正确安装下面引用的库，并正确配置环境同时import进入

import torch
import matplotlib.pyplot as plt
import numpy as np
import cv2 as cv

x = torch.arange(4.0) #定义向量x
x.requires_grad_(True) #开始存储梯度
x.grad #访问梯度

当前访问中x的梯度为None

好让我们继续定义函数，随便定义一个比较简单的函数\(y = 2x^Tx\)

y = 2*torch.dot(x,x) #定义函数y = 2 xT x
y.backward() #求导、反向传递
print(x.grad) #看x的梯度

可以看到结果

我们知道哈\(y=2x^2\)这东西的导数为\(y' = 4x\)那我们验证一下正不正确哈。

Text = x.grad ==4*x
print(Text)

可以看到运行的结果是True说明咱们的反向求导正确了。

现在我们想要重新定义一个新的函数，在使用前一定要先进行之前梯度缓存的清除工作才可以进行创建。

x.grad.zero_() #清除之前的梯度缓存
y = x.sum() #重新建立一个新的函数
print(y)
y.backward() #求导、反向传递
GRAD_x = x.grad #访问梯度
print(GRAD_x)

注意sum就是向量x和全1向量的内积

也就是全部加一起

---

5 finish

5.1 重要函数

1. 星号* ：对于标量也就是一个数据直接相乘 4*4=16，但是对于两个形状相同的向量而言是对应元素相乘。
2. sum()：这个函数的意思就是将其向量本身和一个全1 向量做内积
3. .grad.zero_()：清除缓存。
4. .grad：访问当前梯度，这个默认是false，需要用6的函数进行开启。
5. .backward()：求导、反向传递。
6. .requires_grad_()：开始存储梯度，True允许，False不允许。
7. .detach()：就是将一个东西和本身的这个向量分离，二者无关，可以视作常量。

5.2 代码全部

import torch
import matplotlib.pyplot as plt
import numpy as np
import cv2 as cv
import math

x = torch.arange(4.0) #定义向量x
x.requires_grad_(True) #开始存储梯度
x.grad #访问梯度

y = 2*torch.dot(x,x) #定义函数y = 2 xT x
y.backward() #求导、反向传递

Text = x.grad ==4*x

x.grad.zero_() #清除之前的梯度缓存
y = x.sum() #重新建立一个新的函数
#print(y)
y.backward() #求导、反向传递
GRAD_x = x.grad #访问梯度
#print(GRAD_x)

x.grad.zero_() #清除之前的梯度缓存
y=x*x
# 等价于 y.backward(torch.ones(len(x)))
y.sum().backward() #求导、反向传递
GRAD_x = x.grad
# print(GRAD_x)

x.grad.zero_()
y = x* x #对应元素相乘
print(y)
u = y.detach() #u就相当于一个常量 并不是变量
z = u * x
z.sum().backward() #求导、反向传递
GRAD_x = x.grad
Test = x.grad == u #检验
# print(GRAD_x)
# print(Test)