4 矩阵计算(求导方面)

4 矩阵计算(求导方面)

目录

• 4 矩阵计算(求导方面)
  • 0 引言
  • 1 标量的导数
  • 2 向量和标量的混合导数
  • 3 总结

[!IMPORTANT]

B站视频链接 4 矩阵计算

---

0 引言

这里所谓的矩阵计算并非简单的矩阵之间的加减乘除，而是利用矩阵进行求导的运算，这个运算在今后的设计以及编写过程是非常重要的。

首先 [2 数据操作和数据预处理](E:\typora\1 DeepLearning\1 WithLiMU\2 Data manipulation and preprocessing.md) 中便已经知道了标量、向量以及矩阵的关系，现在就依靠这几个数据类型进行说明和运算。

定义：

• 标量：全是小写的字母 \(a、b\) 。
• 向量：带箭头的小写字母 \(\vec{a} 、\vec{b}\) 。
• 矩阵：大写的字母 \(A 、B\) 。

1 标量的导数

标量就是一个数据，类似于\(1、2、3\)，并非数组或是向、矩阵等。

\(y = f(x)、x\)就是标量 、\(f(x)\)是对应法则 、 \(y\)是自变量$

\(y\)	\(\frac{dy}{dx}\)
\(a\)	\(0\)
\(x^n\)	\(nx^{n-1}\)
\(e^x\)	\(e^x\)
\(lnx\)	\(\frac{1}{x}\)
\(sinx\)	\(cosx\)
\(u(x)+v(x)\)	\(\frac{du}{dx} + \frac{dv}{dx}\)
\(u(x) \times v(x)\)	\(\frac{du}{dx} \times v(x) + \frac{dv}{dx} \times u(x)\)
\(\frac{u(x)}{v(x)}\)	\(\frac{u'v-uv'}{(v')^2}\)

对于不能求导的函数又该怎么办呢？

例如: \(f(x) = |x|\)

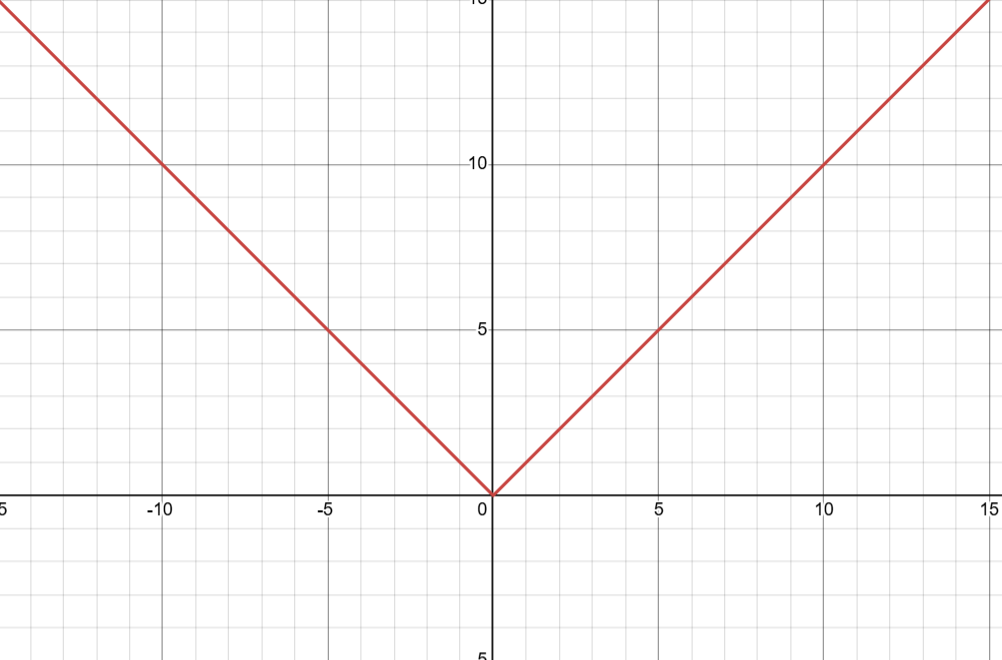
不难看出该函数在\(x>0\)时候\(f'(x) = 1\) ， \(x<0\)时候\(f'(x) = -1\) ， \(x = 0?\)

这个函数在\(x=0\)的位置明显不可导，对于这种不可导的函数又该怎么办呢？

这个时候有一个叫做亚函数，虽然我不知道他有啥用但是应该和偏导数应该类似，这个时候上面的导数可以写成为

\[\frac{\partial |x|}{x} = \left \{ \begin{array}{l} -1 &, x<0\\ 1 &, x>0\\ a &, x=0\\ \end{array} \right. \]

这个时候便可以引入了一个新的数学定义-\(梯度grad\)

[!NOTE]

注意梯度是一个向量而非数据，梯度的方向一定是函数方向导数的最大值

在任意一点\(P(x_1 , x_2 , ... ,x_n)\)的梯度为

\[gradf(p) = (\frac{\partial f}{x_1}|_{P(x_1 , x_2 , ... ,x_n)} , ...,\frac{\partial f}{x_2}|_{P(x_1 , x_2 , ... ,x_n)} ) = (y_1 , y_2,...y_n) \]

2 向量和标量的混合导数

向量和标量之间混合求导会出现下面四种情况

1. \(y是一个标量 ，x也是一个标量 会得到\frac{\partial y}{\partial x }也是一个标量\) 。
2. \(\vec{y}是一个向量 ，也是一个标量 会得到\frac{\partial \vec{y}}{\partial x }是一个向量\) 。
3. \(y是一个标量 ，\vec{x}也是一个向量量 会得到\frac{\partial y}{\partial \vec{x} }也是一个向量 ，但是是一个躺着的向量\) 。
4. \(\vec{y} 和 \vec{x}均为向量,那么\frac{\partial \vec{y}}{\partial \vec{x} } 就是一个矩阵A\) 。

举个例子说明一下吧：

\[\text{令}\overline{y}=\left[ \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n\\ \end{array} \right] \,\,,\,\,\overline{x}=\left[ \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n\\ \end{array} \right] \text{则}\frac{\partial \overline{y}}{\partial \vec{x}}=\left[ \begin{array}{c} \frac{\partial y_1}{\partial \vec{x}}\\ \frac{\partial y_2}{\partial \vec{x}}\\ \vdots\\ \frac{\partial y_n}{\partial \vec{x}}\\ \end{array} \right] =\left[ \begin{matrix}{l} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \cdots& \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \cdots& \frac{\partial y_2}{\partial x_n}\\ \vdots& \vdots& \cdots& \vdots\\ \frac{\partial y_n}{\partial x_1}& \frac{\partial y_n}{\partial x_2}& \cdots& \frac{\partial y_n}{\partial x_n}\\ \end{matrix} \right] \]

3 总结

y如果是向量的话这个是竖着的。

x如果是向量的话这个是躺着的。