变换(旋转、缩放、平移)
1、为什么要学习变换矩阵
- 模型的缩放、旋转、位移都可以通过变换矩阵实现
- 投影:将3D的世界转换为2D的图片
2、二维变换
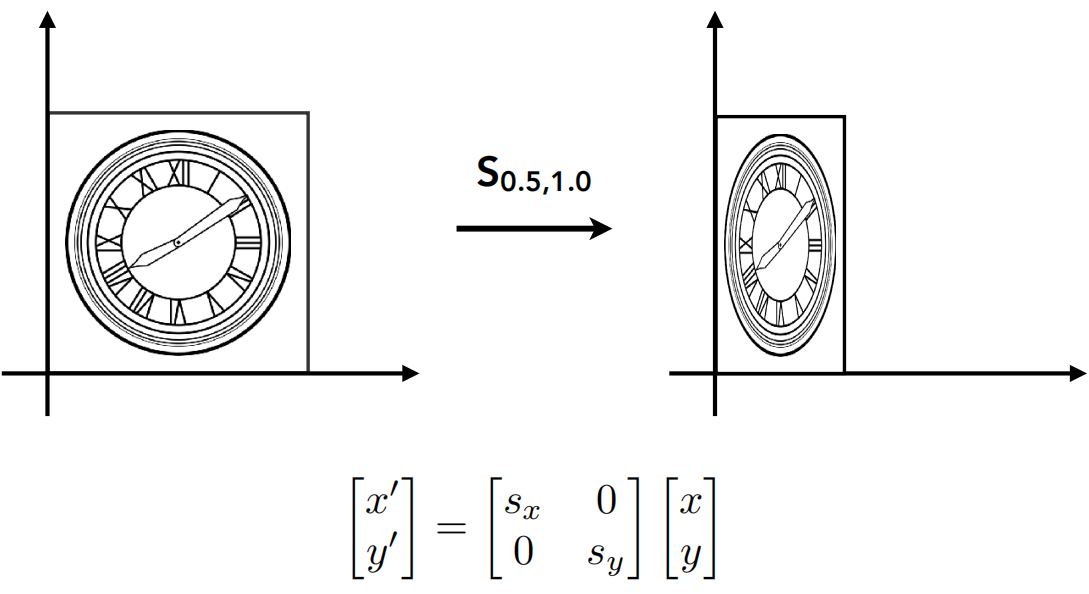
Scale 缩放
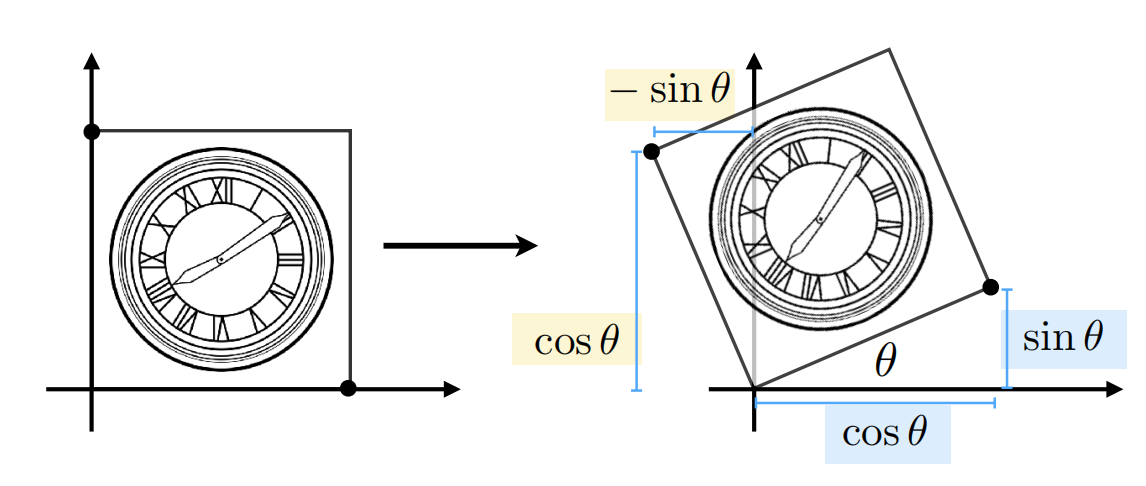
Rotate 旋转
-
默认绕原点(0,0) 逆时针方向旋转
-
思路:旋转不改变长度大小,从特殊点推导旋转矩阵
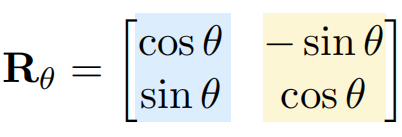
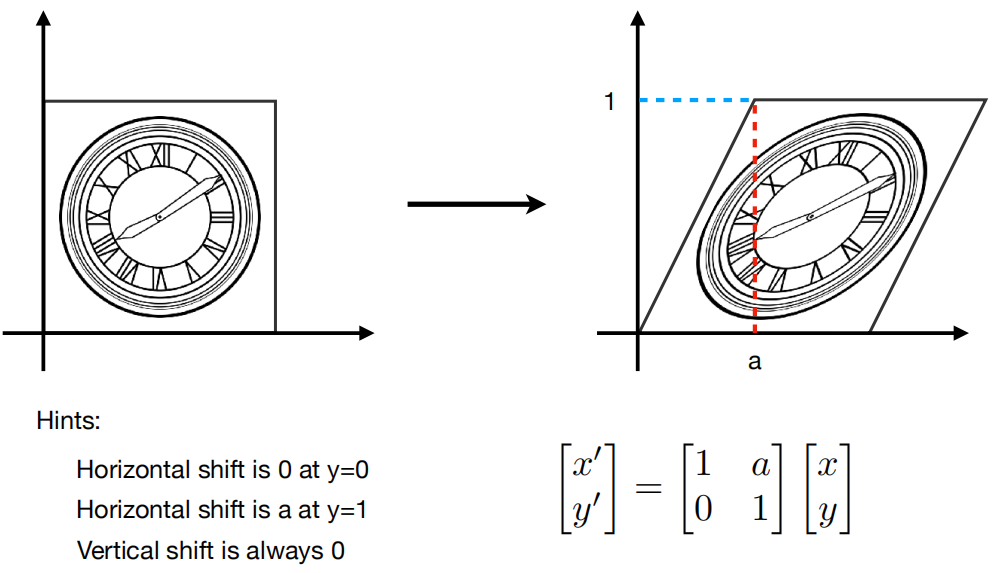
Shear 裁切
- 把物体一边固定,然后拉另外一边
3、齐次坐标
为什么
-
位移变换无法用线性变换表示 (可以理解为无法用一个矩阵表示变换)
-
无法用两个矩阵乘积的形式表示平移变换
![]()
是什么
-
其实就是引入一个
w坐标w = 1表示这是一个点 (w≠0都认为是点)w = 0表示这是一个向量

-
注意代入齐次坐标之后向量与点之间的运算以及结果
-
现在位移变换也可以表示位矩阵乘积的形式了
- 如果对一个向量进行位移变换时向量的值不会变(
w=0),这是符合事实的
- 如果对一个向量进行位移变换时向量的值不会变(
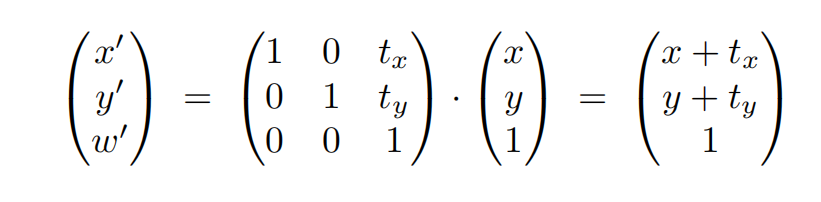
Affifine map 仿射变换
-
线性变换 + 平移变换
![]()
引入齐次坐标后的二维变换

复合变换
- 对模型的一系列变换的组合可以用一个变换矩阵表示
- 矩阵的乘法不满足交换律,不同的顺序得到的结果是不一样的
- 复合变换约定顺序
- 缩放 —> 旋转 —> 平移
4、三维变换
- 3D point = (x, y, z,1)T
- 3D vector = (x, y, z,0)T
旋转
-
三维的旋转比较特殊,总结起来就是
-
绕谁谁不变,y轴旋转最特殊
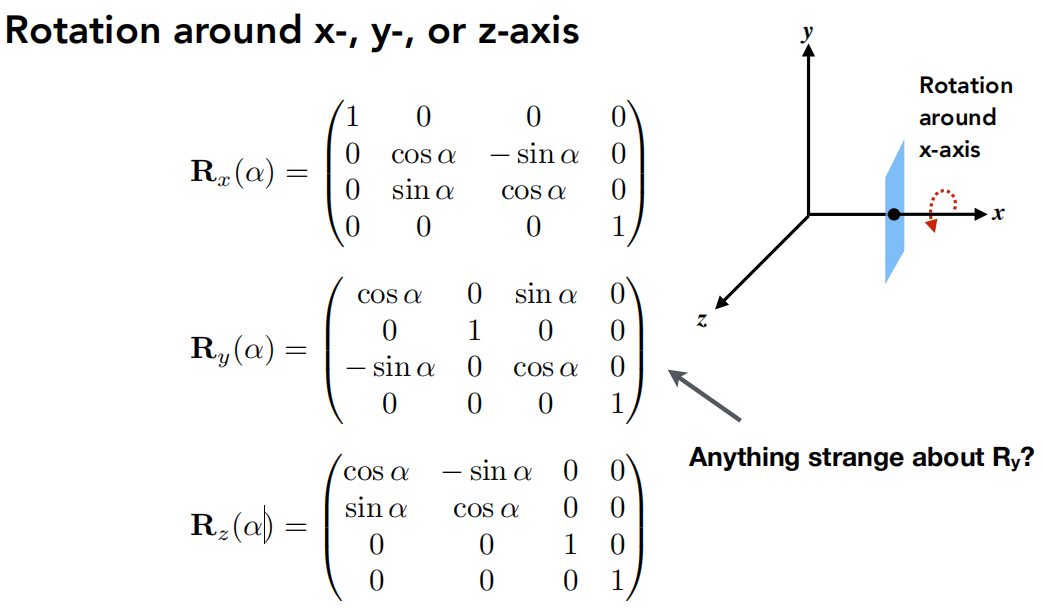
4.1 欧拉角
为什么
- 实际中有物体可能不绕
xyz轴旋转,而是绕任意轴旋转
是什么
-
可以把一个旋转拆分成绕
xyz轴的旋转,这三个角度被称为欧拉角![]()
-
优点是表达和公式很直观
-
缺点:
- 不可传递,旋转顺序影响旋转结果
- 万向节死锁
4.2 万向节死锁
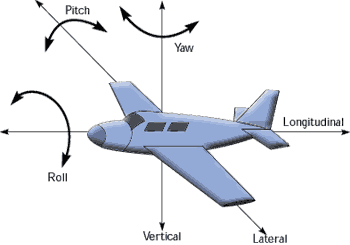
转动的术语
- 沿着机身右方轴进行旋转 Pitch 俯仰
- 沿着机头上方轴进行旋转 Yaw 偏航
- 沿着机头前方轴进行旋转 Roll 桶滚
出现死锁
- 按照欧拉角的定义,需要有三个自由度来表示旋转

-
出现死锁的情况
- 红色连接头:可以给予一个相对俯仰的自由度
- 绿色连接头:可以给予一个相对偏航的自由度
- 蓝色连接头:可以给予一个相对偏航的自由度
-
这里桶滚自由度丢失了,只有两个自由度,无法表示需要三个自由度的旋转,产生了死锁
解决方法
- 使用绕任意轴旋转的方式表达旋转
- 轴角和罗德里格斯公式
- 四元数
4.3 轴角和罗德里格斯公式
轴角
用两个值参数化旋转:轴和绕这个轴旋转的角度。{x,y,z, Ѳ }
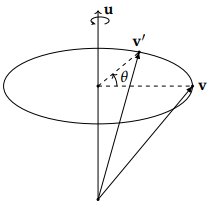
\[v' = R*v
\]
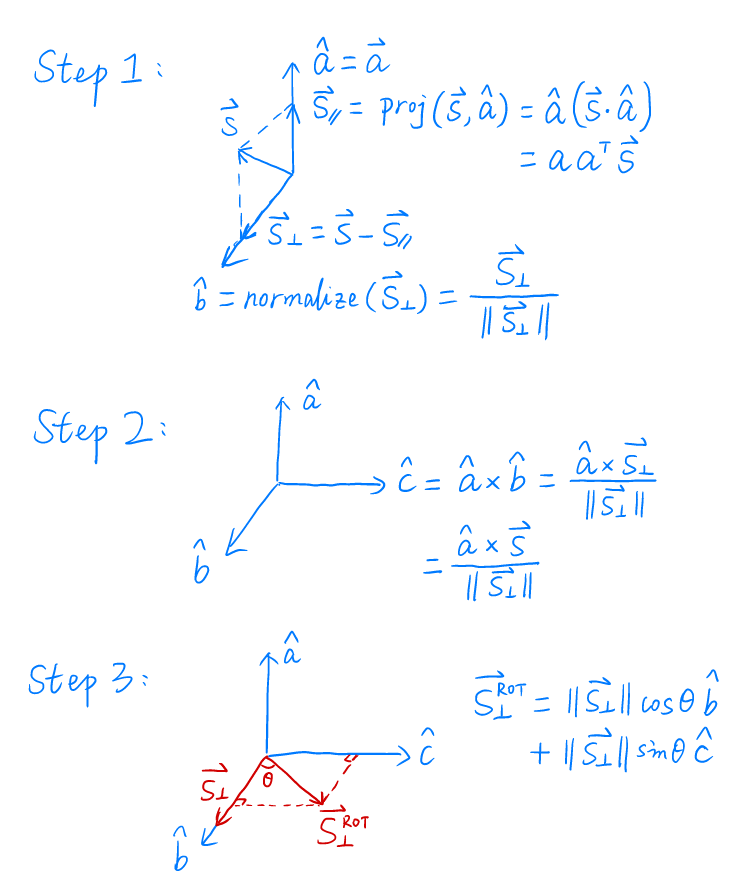
罗德里格斯公式
-
绕一个轴
n旋转α角度的旋转矩阵![]()
-
证明思路
- 设向量
S绕a轴旋转θ角度,求向量S^ROT- 将向量
S通过点积投影的方式分解为平行和垂直于a轴的分量- 平行分量在旋转后不变
- 求出旋转后
S^ROT的垂直分量即可
- 将向量
- 设向量
4.4 四元数
为什么
- 解决欧拉角表示旋转的死锁问题
- 轴角虽然能解决死锁问题,但是不能进行简单的插值
是什么
-
包含一个标量和一个三维向量分量 (节省内存,只要4个浮点数就可以表示一个旋转)
Q=[w,(x,y,z)]^T -
绕旋转轴
n旋转α的旋转,用四元数表示为- 余弦值的角度为旋转轴的
x,y,z分量
![]()
- 余弦值的角度为旋转轴的
使用四元数表示旋转
- 给定矢量
V和旋转的单位四元数q - 旋转后的矢量
V^ROT = q . V . q^-1
转换
-
欧拉角转四元数
![]()
-
四元数转欧拉角
![]()
插值
-
从A旋转到B中间的插值
![]()
旋转表示方式问题总结
- 矩阵:内存消耗大,插值问题
- 欧拉角:万向节死锁问题,不可传递(顺序决定结果)
- 轴-角:插值问题,不能直接作用于点和矢量,还是要转换为四元素或者矩阵
- 四元数:插值平滑,可以快速和矩阵形式转换,节省内存


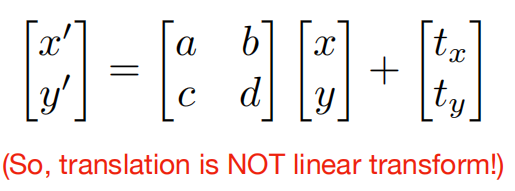

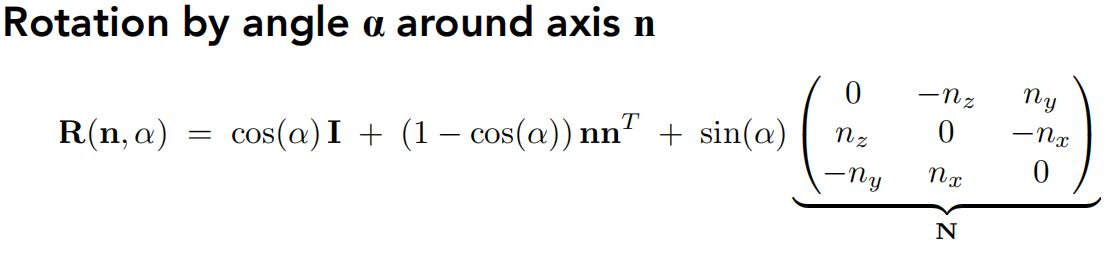
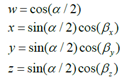
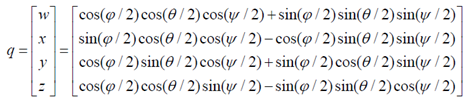

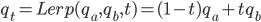

 浙公网安备 33010602011771号
浙公网安备 33010602011771号