sunday算法
1、简介
- 思路很简单同时效率又强过KMP和BM的算法
2、思路分析
-
这里引用别人的例子来分析
- 主串:“LESSONS TEARNED IN SOFTWARE TE”
- 模式串:“SOFTWARE”
-
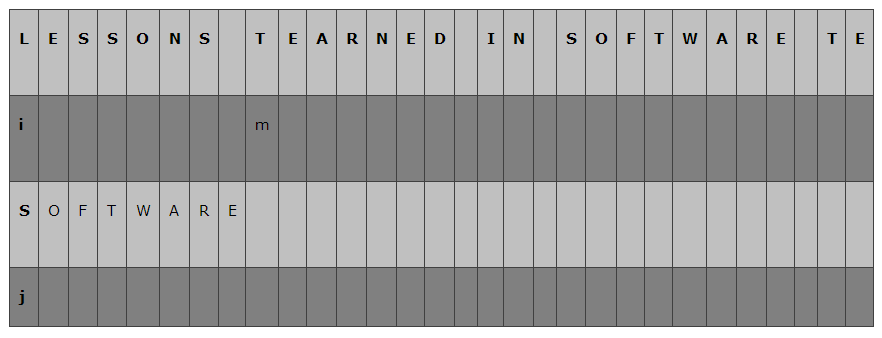
开始比较:
- 比较方式和一般的模式匹配并没有什么不同,开始时
i=0,j=0从左到右逐字符比较 - 当有字符匹配失败时(这里第一个字符就没有匹配),sunday算法有了自己的想法
![]()
- 比较方式和一般的模式匹配并没有什么不同,开始时
-
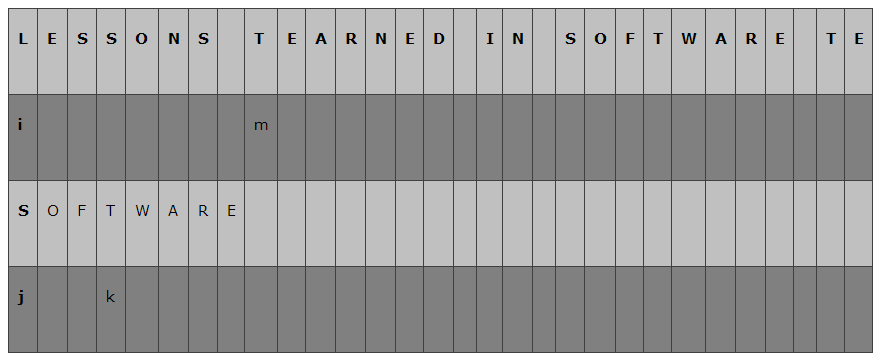
匹配失败:
- 首先我们要找到当前匹配主串最后一个字符的下一个字符(这里就是m指向的位置)
- 然后们从模式串的最后一个位置向前查找第一个相同的字符(这里我们找到了k指向的位置)
![]()
-
对齐相等的字符:
- 将上一步中我们找到的两个字符对齐
- 实际操作上是我们根据一定的规则改变主串下标
i的值,并将j设为0重新开始比较
![]()
-
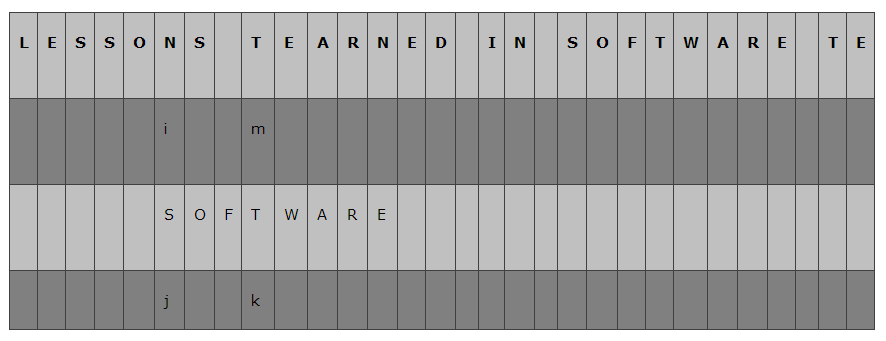
一种特殊的情况:模式串中不存在相同的字符
- 这里我们发现模式串中并没有
m指向的字符D,这说明- 从
i到m之间肯定不存在匹配的字串 m指向的位置也肯定不匹配
- 从
- 所以我们应该将
i移动到m+1,令j=0重新开始匹配
![]()
- 这里我们发现模式串中并没有
3、代码
- 这里选择了一段我个人认为比较好理解的代码
- 注释应该写得很清楚了
shift矩阵
- 要理解shift矩阵的下标对应的是字符的ASCII码
- 注意看设置shift初值和使用的方式
- shift存储的是字符匹配不相等时主串下标
i应该移动的距离- 如果模式串中不存在对应的字符,按照前面的分析我们应该将
i移动到m+1(这就是shift默认值的意义)
- 如果模式串中不存在对应的字符,按照前面的分析我们应该将
#include <iostream>
#include <string>
using namespace std;
#define maxNum 1005
int shift[maxNum];
int Sunday(const string& T, const string& P) {
int n = T.length(); //主串长度
int m = P.length(); //模式串长度
//预处理 更新shift矩阵
//--------------------
//默认值 移动m + 1位(模式串中没有出现的字符,应该忽略包括这个字符在内之前的所有字符)
for(int i = 0; i < maxNum; i++)
shift[i] = m + 1;
//记录每个模式串中出现的字符需要移动的距离
//相同的字符会覆盖,只记录最后出现的
for (int i = 0; i < m; i++)
shift[P[i]] = m - i;
//匹配开始位置
int k = 0; //主串下标,始终指向正在匹配的主串的第一位
int j = 0; //模式串下标
//匹配算法
//------
while (k <= n - m) {
j = 0;
while (T[k + j] == P[j]) { //注意这里k的值没有变
j++;
if (j >= m)//匹配成功
return k;
}
//T[k+m]: 正在匹配的主串最后一个元素的下一个元素
//移动主串下标,在下一个循环中重新匹配(从第一个字符开始)
k += shift[T[k + m]];
}
return -1;
}
4、算法分析
- 空间复杂度:shift矩阵的大小,为常数级
maxNum - 时间复杂度
- 预处理时间:
O(maxNum+m) - 平均时间复杂度:
O(n) - 最坏情况下时间复杂度:
O(mn)
- 预处理时间:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号