概率期望DP做题记录-Part2
概率期望DP做题记录-Part2
Part1
CF804D Expected diameter of a tree
题意
给定一片森林。
\(q\) 次询问,每次给定两个点,问将这两个所在的联通块连起来之后,这个大联通块的直径的期望。
\(n\le 10^5\)。
做法
首先,期望的式子是很好推的。
设 \(d(x,y)\) 为将 \(x\) 和 \(y\) 连起来后的直径,\(siz_x\) 表示 \(x\) 所在联通块的大小,\(S_u\) 表示 \(u\) 所在的联通块,那么将 \(u\) 和 \(v\) 所在连接的答案就是:
分母是好求的,考虑如何求出分子。
设 \(d(u)\) 表示 \(u\) 所在的联通块的直径,\(dis_u\) 表示联通快内到 \(u\) 最远的点的距离,那么 \(d(i,j)\) 就等于:
在继续往下写之前,先考虑一下如何求出 \(dis\)。
有一个结论:在一棵树上,任选一条直径,到任意一个点最远的一个点一定可以是这条直径的两个端点之一。
这个东西的证明可以去康康hegm的博客。在里面
Ctrl+F搜索区间树上最远点对即可。所以,对于每个联通块,仅需进行三遍dfs即可求出它的 \(dis\),复杂度 \(\Theta(n)\)。
如果只有第一项或者只有最后两项,这个式子是非常好算的。
这是一个取 \(\max\) 的式子,所以考虑在什么时候能取到 \(dis_u+dis_v+1\)。显然是要:
既然如此,我们对每棵树开一棵值域线段树,然后枚举 \(A\) 树上的所有点,在 \(B\) 树的值域线段树上查询 \([\max\{d(u),d(v)\}-dis_u-1,n]\) 的点的数量和这些点 \(dis\) 的和即可。
显然,现在我们可以在 \(\min\{|S_u|,|S_v|\}\log n\) 的时间内处理一组询问。
观察题解,考虑使用根号分治。
- 当 \(\min\{|S_u|,|S_v|\}\le\sqrt{n}\) 时,直接按照上面的暴力计算即可。显然这里的复杂度是 \(O(q\sqrt{n}\log_2n)\) 的。
- 容易发现,\(|S|\ge\sqrt{n}\) 的 \(S\) 不会超过 \(\sqrt{n}\) 个,这样的询问不会超过 \(\sqrt{n}\times\sqrt{n}=n\) 个。
- 于是我们预处理出这些答案,开一个map存起来。这样预处理的复杂度是 \(O(n\sqrt{n}\log_2n)\) 的。
- 我们枚举这样较大的树对,然后枚举其中一棵树中的所有点,对另一棵树的值域线段树进行查询即可。
考虑枚举这些集合的过程。
这个过程就相当于,对于每个在较大集合中的点,都枚举一遍所有的较大的集合。
显然所有点加起来不会超过 \(O(n)\),较大的集合数量不会超过 \(O(\sqrt{n})\),单次查询是 \(\Theta(\log_2n)\) 的。
所以,这里的复杂度就是 \(O(n\sqrt{n}\log_2n)\) 的。
综上,这样根号分治的复杂度就是 \(O(q\sqrt{n}\log_2n+n\sqrt{n}\log_2n)\)。
当然,作者在写的时候脑子抽了,这个是可以不用值域线段树实现的,只需要开一个vector存即可。这样的复杂度是 \(O(n\sqrt{n}+q\sqrt{n})\) 的,也省去了值域线段树,代码长度也能更短一些。但写了已经写了,于是就这样了。
具体细节见代码。
代码
写得恶臭,长度约3.87KB。
#include<bits/stdc++.h>
using namespace std;
inline int read(){//快读
int ans=0;bool op=0;char ch=getchar();
while(ch<'0'||'9'<ch){if(ch=='-')op=1;ch=getchar();}
while('0'<=ch&&ch<='9'){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}
if(op)return -ans;
return ans;
}
const int maxn=1e5+10;
struct node{
int l,r,cnt,val;
}tr[maxn<<5];//动态开点线段树
int n,m,q;
int BLOCK_SIZ;//根号分治的块长
int cnt=0;
int root[maxn];//最多n棵动态开点线段树,记录n个根
vector<int>g[maxn];
int dis[maxn];//如题
int fa[maxn];//并查集
int clr[maxn],col;
int fst[maxn],lst[maxn];//直径的起点和终点
int dep[maxn];
vector<int>s[maxn];//记录一个联通块中有哪些点
vector<int>big_tr;//记录较大的树都有哪些
map<int,map<int,double>>anss;//预处理的ans
void newnode(int &p){
tr[++cnt]=(node){0,0,0,0};
p=cnt;
}
void pushup(int p){
tr[p].cnt=tr[tr[p].l].cnt+tr[tr[p].r].cnt;
tr[p].val=tr[tr[p].l].val+tr[tr[p].r].val;
}
void add(int pos,int s,int t,int &p,int val){//单点加的实现
if(!p)newnode(p);
if(s==pos&&pos==t){
++tr[p].cnt;
tr[p].val+=pos;
return;
}
int mid=(s+t)>>1;
if(pos<=mid)add(pos,s,mid,tr[p].l,val);
else add(pos,mid+1,t,tr[p].r,val);
pushup(p);
}
void add(int pos,int val,int _){//单点加
add(pos,0,n,root[_],val);
}
pair<int,int> query(int l,int r,int s,int t,int p){//区间查询的实现
if(!p)return make_pair(0,0);
if(l<=s&&t<=r)return make_pair(tr[p].cnt,tr[p].val);
int mid=(s+t)>>1;
pair<int,int>ans=make_pair(0,0);
if(l<=mid){
pair<int,int>tmp=query(l,r,s,mid,tr[p].l);
ans=tmp;
}
if(mid<r){
pair<int,int>tmp=query(l,r,mid+1,t,tr[p].r);
ans.first+=tmp.first;
ans.second+=tmp.second;
}
return ans;
}
pair<int,int> query(int l,int r,int _){//区间查询
return query(l,r,0,n,root[_]);
}
/*到这里是线段树 到这里是线段树 到这里是线段树 到这里是线段树 到这里是线段树 到这里是线段树 到这里是线段树 到这里是线段树*/
int find(int now){//并查集查询
if(fa[now]==now)return now;
return fa[now]=find(fa[now]);
}
void dfs1(int now,int fa){//第一遍dfs
clr[now]=col;
s[col].push_back(now);
dep[now]=dep[fa]+1;
if(dep[now]>dep[fst[col]])fst[col]=now;
for(int nxt:g[now]){
if(nxt==fa)continue;
dfs1(nxt,now);
}
}
void dfs2(int now,int fa){//第二遍dfs
dep[now]=dep[fa]+1;
dis[now]=dep[now]-1;
if(dep[now]>dep[lst[col]])lst[col]=now;
for(int nxt:g[now]){
if(nxt==fa)continue;
dfs2(nxt,now);
}
}
void dfs3(int now,int fa){//第三遍dfs
dep[now]=dep[fa]+1;
dis[now]=max(dis[now],dep[now]-1);
add(dis[now],1,clr[now]);
for(int nxt:g[now]){
if(nxt==fa)continue;
dfs3(nxt,now);
}
}
signed main(){
n=read(),m=read(),q=read();
BLOCK_SIZ=sqrt(n)+1;//设置块长
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u=read(),v=read();
fa[find(u)]=find(v);
g[u].push_back(v),g[v].push_back(u);
}
for(int i=1;i<=n;i++){//处理联通快
if(!clr[i]){
++col;
dfs1(i,0);
dfs2(fst[col],0);
dfs3(lst[col],0);
}
}
for(int i=1;i<=col;i++){//记录哪些树是大树
if(query(0,n,i).first>=BLOCK_SIZ)big_tr.push_back(i);
}
for(int i:big_tr){//枚举所有大树,预处理答案
int di=dis[fst[i]];
int si=query(0,n,i).first;
for(int j:big_tr){
if(i==j)continue;
int dj=dis[fst[j]];
int sj=query(0,n,j).first;
double ans=0;
int cnt=0;
for(int k:s[i]){
pair<int,int>tmp=query(max(max(di,dj)-dis[k]-1,0),n,j);
ans+=1.0*tmp.second+tmp.first*(dis[k]+1);
cnt+=tmp.first;
}
ans+=1.0*(si*sj-cnt)*max(di,dj);
ans/=1.0*si*sj;
anss[find(fst[i])][find(fst[j])]=ans;
anss[find(fst[j])][find(fst[i])]=ans;
}
}
for(int i=1;i<=q;i++){//q次询问
int u=find(read()),v=find(read());
if(u==v){
puts("-1");
continue;
}
int su=query(0,n,clr[u]).first,sv=query(0,n,clr[v]).first;
if(su>sv)swap(u,v),swap(su,sv);
if(su>=BLOCK_SIZ)cout<<fixed<<setprecision(10)<<anss[u][v]<<'\n';//大树,输出预处理的答案
else{//小树,暴力查询
int du=dis[fst[clr[u]]];
int dv=dis[fst[clr[v]]];
double ans=0;
int cnt=0;
for(int k:s[clr[u]]){
pair<int,int>tmp=query(max(max(du,dv)-dis[k]-1,0),n,clr[v]);
ans+=1.0*tmp.second+tmp.first*(dis[k]+1);
cnt+=tmp.first;
}
ans+=1.0*(su*sv-cnt)*max(du,dv);
ans/=1.0*su*sv;
cout<<fixed<<setprecision(10)<<ans<<'\n';
}
}
return 0;
}
P4562 [JXOI2018]游戏
题意
九条可怜负责管理 \(n\) 个办公室,编号为 \(l\sim r\)。
员工会偷懒,但是当她检查某个办公室时,这个办公室的员工会开始认真工作,并且通知编号是它倍数的其他办公室的员工也开始认真工作。
对于每种顺序 \(p\),存在一个最小时间 \(t(p)\),使得可怜按照这个顺序检查完前 \(t(p)\) 个办公室后,所有的办公室都会开始认真工作。
现在需要求出所有 \(t(p)\) 的和,答案对 \(10^9+7\) 取模。
\(l,r\le 10^7\)。
做法
考虑对于一个排列 \(p\),如何求出 \(t(p)\)。
观察题解发现,\([l,r]\) 中的数可以分为两类:
- 是 \([l,r]\) 中某个数的倍数的。
- 不是 \([l,r]\) 中某个数的倍数的。
根据定义,当且仅当第二类数都出现过时,\([l,r]\) 被完整覆盖。那么不妨设有 \(k\) 个二类数。
考虑求出 \(t(p)=i\) 的 \(p\) 的方案数。首先,\(t(p)=i\) 表示,在 \(i\) 位置必须有一个二类数,在前 \(i-1\) 个位置要有 \(k-1\) 个二类数。那么 \(t(p)=i\) 的方案数就是:
那我们仅需求出 \(\sum_{i=1}^n i\times\binom{i-1}{k-1}\times k!\times (n-k)!\) 即可。
那么:
然后直接计算即可。
需要注意的是,我们可以在做乘法的时候特判掉 \(k+1\),这样就不用求逆元了。
代码
signed main(){
l=read(),r=read();
n=r-l+1;
for(int i=l;i<=r;i++){
if(!vis[i]){
++m;
for(int j=2;i*j<=r;j++)vis[i*j]=1;
}
}
ans=m;
for(int i=1;i<=n+1;i++)if(i!=m+1)ans=(ans*i)%mod;
cout<<ans;
return 0;
}
P6835 [Cnoi2020]线形生物
题意
给定一个从 \(1\) 号点到 \(n+1\) 号点的链子,边形如 \((i,i+1)\)。
现在加入 \(m\) 条返祖边。返祖边形如 \((u,v)\),其中 \(u\ge v\)。
你在这个图上随机游走,问走到 \(n+1\) 号点的步数的期望。
\(n\le 10^6\)。
做法
观察题解,我们获得了一个全新的套路。
一般地,对于一个随机游走的问题,我们可以设 \(f_i\) 表示从 \(i\) 走到 \(i+1\) 的期望步数。
利用期望的线性性质,从 \(1\) 走到 \(n+1\) 的步数期望 \(E(1\rightarrow n+1)=\sum_{i=1}^nf_i\)。
然后只需要考虑如何求出 \(f_i\) 即可。
考虑如何求出 \(f_i\)。
这个东西看起来有后效性,我们观察题解,得到解决方法。
先写出朴素的转移式子(\(d_i\) 表示点 \(i\) 的度数),然后进行化简:
利用期望的线性性质,可以得到:
设 \(sum_i\) 表示 \(\sum_{k=1}^if_k\),那么我们就可以用前缀和快速求出 \(\sum_{k=y}^xf_k\) 了。那么上式就变为:
然后按照式子转移即可。
代码
signed main(){
id=read(),n=read(),m=read();
for(int i=1;i<=n;i++){
g[i].push_back(i+1);
}
for(int i=1;i<=m;i++){
int u=read(),v=read();
g[u].push_back(v);
}
for(int i=1;i<=n;i++){
f[i]=g[i].size();
for(int j:g[i]){
if(j==i+1)continue;
f[i]=(f[i]+sum[i-1]-sum[j-1]+mod)%mod;
}
sum[i]=(sum[i-1]+f[i])%mod;
}
for(int i=1;i<=n;i++)ans=(ans+f[i])%mod;
cout<<ans<<endl;
return 0;
}
P6834 [Cnoi2020]梦原
题意
给定一个 \(n\) 个节点的无根树,节点 \(i\) 上有 \(a_i\) 个果实,每次操作可以选择一个联通块并摘下每个节点上的一个果实,求最少需要多少次操作才能将所有果实摘完的期望。
节点 \(i\) 会等概率地从区间 \([i-k,i-1]\) 中选择一个节点连接,其中 \(k\) 是一个已知常数。
\(n\le 10^6\)。
做法
首先,设 \(dp_i\) 表示摘完 \(1\sim i\) 节点上的果实的期望操作次数,考虑转移。
考虑加入一个点会产生的贡献。分两种情况讨论(设当前点编号为 \(i\),要接到 \(j\) 号点上):
- 如果 \(a_i\le a_j\),那么在取 \(a_j\) 的时候可以顺便把 \(a_i\) 取完,所以不会产生额外贡献。
- 如果 \(a_i>a_j\),那么在取完 \(a_j\) 时,\(a_i\) 还会剩下 \(a_i-a_j\),这是额外产生的贡献。
然后我们就有了一个愉快的转移式子:
容易发现,这样直接转移的复杂度是 \(\Theta(nk)\) 的。
观察讨论发现,这里可以直接用值域线段树扫过去,只是空间会炸,离散化即可。
这样的时间复杂度是 \(\Theta(n\log_2m)\) 的,空间复杂度是 \(O(n)\) 的。
代码
恶臭代码,2.13KB。
const int maxn=1e6+10;
const int mod=998244353;
int n,m;
int a[maxn];
int dp[maxn];
vector<int>mp;
struct node{
int l,r,cnt,sum;
}tr[maxn<<1];
int root,cnt;
void newnode(int &p){
p=++cnt;
tr[p]=(node){0,0,0,0};
}
void add(int pos,int s,int t,int &p,int num){//单点加入一个元素
if(!p)newnode(p);
if(s==pos&&pos==t){
tr[p].cnt+=num;
tr[p].sum+=mp[pos]*num;
return;
}
int mid=(s+t)>>1;
if(pos<=mid)add(pos,s,mid,tr[p].l,num);
else add(pos,mid+1,t,tr[p].r,num);
tr[p].cnt=(tr[tr[p].l].cnt+tr[tr[p].r].cnt)%mod;
tr[p].sum=(tr[tr[p].l].sum+tr[tr[p].r].sum)%mod;
}
int get_cnt(int l,int r,int s,int t,int p){//查询一个值域内的元素数量
if(!p)return 0;
if(l<=s&&t<=r)return tr[p].cnt;
int mid=(s+t)>>1,ans=0;
if(l<=mid)ans+=get_cnt(l,r,s,mid,tr[p].l);
if(mid<r)ans+=get_cnt(l,r,mid+1,t,tr[p].r);
return ans;
}
int get_sum(int l,int r,int s,int t,int p){//查询一个值域内的元素的值的和
if(!p)return 0;
if(l<=s&&t<=r)return tr[p].sum;
int mid=(s+t)>>1,ans=0;
if(l<=mid)ans+=get_sum(l,r,s,mid,tr[p].l);
if(mid<r)ans+=get_sum(l,r,mid+1,t,tr[p].r);
return ans;
}
void add(int pos,int num){//偷懒
add(pos,0,n,root,num);
}
int getcnt(int l,int r){
return get_cnt(l,r,0,n,root);
}
int getsum(int l,int r){
return get_sum(l,r,0,n,root);
}
int inv(int x){
int ans=1;
for(int i=mod-2;i;i>>=1){
if(i&1)ans=(ans*x)%mod;
x=(x*x)%mod;
}
return ans;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)mp.push_back(a[i]);
sort(mp.begin(),mp.end());//离散化
mp.erase(unique(mp.begin(),mp.end()),mp.end());//离散化
for(int i=1;i<=n;i++)a[i]=lower_bound(mp.begin(),mp.end(),a[i])-mp.begin();//离散化
dp[1]=mp[a[1]];//特殊处理第一项
add(a[1],1);
for(int i=2;i<=n;i++){
int lc=getcnt(0,a[i]-1),ls=getsum(0,a[i]-1);
int rc=getcnt(a[i],mod);
dp[i]=(dp[i-1]+((lc*mp[a[i]]-ls+mod)%mod)*inv(lc+rc))%mod;//转移
add(a[i],1);//加入当前点的贡献
if(i-m>0)add(a[i-m],-1);//删除多于的贡献
}
cout<<dp[n];//输出
return 0;
}
P2059 [JLOI2013] 卡牌游戏
题意
有 \(N\) 个人坐一圈玩卡牌游戏,总共有 \(M\) 张卡牌,每次庄家从卡牌堆中随机选一张卡牌,将从庄家数第 \(X\) 个人淘汰,被淘汰的人的下家成为新的庄家。
现在已经知道了每张卡牌上的数字,求每个人获胜的概率。
说句闲话
本人在做的时候看错题了,以为每张牌抽出来之后就不放回去了。
然后就想到了一个肥肠美妙的性质:每个抽排方式出现的概率是相等的。
然后就在这个小小的性质里面挖呀挖呀挖,考虑求出每个人获胜的可能得排列数。
然后就寄了。
做法
考虑设一个正序的状态。
然后发现这样的状态不好转移,需要记录存在的人什么的,直接和多项式说再见。
那么我们考虑反向转移。设 \(dp_{i,j}\) 为还剩 \(i\) 人时,从庄家往后数第 \(j\) 个人的胜率。
显然,\(dp_{1,1}=1\)。这是初始状态。
考虑转移。肯定要枚举 \(i\) 和 \(j\) 的,然后考虑枚举每张牌。这时,我们可以知道这个位置会去到哪里。
不难发现,这次会删掉的是第 \(a_k\bmod i\) 个人,\(a_k\) 表示第 \(k\) 张牌上的数。那么下次会去到的位置就是:
- 如果 \(a_k\bmod i=j\),\(j\) 直接出局,无缘胜利。
- 如果 \(a_k\bmod i<j\),\(j\) 前面有 \(a_k\bmod i\sim j\),所以 \(j\) 会在 \(j-a_k\bmod i\)。
- 如果 \(a_k\bmod i>j\),\(j\) 前面有 \(a_k\bmod i\sim i\) 加上 \(1\sim j\),所以 \(j\) 会在 \(j+i-a_k\bmod i\)。
现在,我们知道了从哪转移,然后直接转移即可。
代码
signed main(){
n=read(),m=read();
for(int i=1;i<=m;i++)a[i]=read();
dp[1][1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
for(int k=1;k<=m;k++){
if(a[k]%i==j)continue;
if(a[k]%i<j)dp[i][j]+=dp[i-1][j-a[k]%i]/m;
else dp[i][j]+=dp[i-1][j+i-a[k]%i]/m;
}
}
}
for(int i=1;i<=n;i++)cout<<fixed<<setprecision(2)<<dp[n][i]*100<<"% ";//百分比输出
return 0;
}
UVA11021 Tribles
题意
一开始有 \(k\) 只鸟。
这种鸟只能活 \(1\) 天,死的时候有\(p_i\)的概率产生 \(i\) 只鸟(一毛一样,也只能活一天)。
问 \(m\) 天内所有鸟都死的概率。
做法
设 \(f_i\) 表示一只鸟在 \(i\) 天内挂掉的概率。
为什么是一只鸟呢?因为鸟与鸟之间互不影响,所以概率可以直接相乘。所以 \(k\) 只鸟在 \(i\) 天内挂掉的概率就是 \(f_i^k\)。
然后就有了转移方程:
直接转移即可。
代码
void real_main(){
n=read(),k=read(),m=read();
for(int i=0;i<n;i++)cin>>p[i];
for(int i=1;i<=m;i++)dp[i]=0;
dp[1]=p[0];
for(int i=2;i<=m;i++){
double base=1;
for(int j=0;j<n;j++){
dp[i]+=p[j]*base;
base*=dp[i-1];
}
}
printf("Case #%d: %.7lf\n",id,ksm(dp[m],k));
}
signed main(){
T=read();
for(id=1;id<=T;id++)real_main();
return 0;
}
UVA1639 糖果 Candy
题意
有两个盒子各有 \(n(n\le 2\times 10^5)\) 个糖。
每天随机选一个盒子(概率分别为 \(p,1-p\)),然后吃一颗糖。直到有一天,打开盒子一看,没糖了!
输入 \(n,p\),求此时另一个盒子里糖的个数的数学期望。
不知道对不对的做法
设 \(dp_{i,j}\) 表示左边取了 \(i\) 个,右边取了 \(j\) 个的概率。
不难发现这个东西是 \(\Theta(n^2)\) 的。考虑推推式子,优化一下复杂度,然后没推出来。
做法
考虑每种取法的概率。
设当前左边空了,右边还剩 \(i\) 块糖。那么我们之前就取过 \(2n+1-i\) 块糖。因为最后一次一定是取了左边,那未确定的就有 \(2n-i\) 次。那么就有 \(\binom{2n-i}{n}\) 种选法,每种选法的概率是 \(p^{n+1}\times(1-p)^{n-i}\)。因为这些选法两不相容,所以根据有限可加性,这样的概率就是 \(\binom{2n-i}{n}\times p^{n+1}\times(1-p)^{n-i}\)。
同理,右边空了,左边剩 \(i\) 个的概率就是 \(\binom{2n-i}{n}\times(1-p)^{n+1}\times p^{n-i}\)。
现在有了概率,计算期望即可。
那么期望就是:
需要注意的是,这里计算组合数会溢出。观察题解发现,这里取个 \(\ln\) 再乘回去就行了。
代码
#define ld long double
void real_main(){
ans=0;
_p=log(1-p);
p=log(p);
for(int i=0;i<=n;i++){
ld l=fact[2*n-i]-fact[n]-fact[n-i]+(n+1)*p+(n-i)*_p;
ld r=fact[2*n-i]-fact[n]-fact[n-i]+(n+1)*_p+(n-i)*p;
ans+=1.0*i*(exp(l)+exp(r));
}
printf("Case %d: %.6lf\n",id,ans);
}
signed main(){
for(int i=1;i<=4e5+5;i++)fact[i]=fact[i-1]+log(i);
while(cin>>n>>p){
++id;
real_main();//多测
}
return 0;
}
P3239 [HNOI2015]亚瑟王
题意
你在玩一个卡牌游戏。你有 \(n\) 张牌,和 \(m\) 个回合。
在每个回合开始时会进行以下操作:
从第一张牌开始考虑。
- 如果这张卡牌在这一局游戏中已经发动过技能,则
1. 如果这张卡牌不是最后一张,则跳过之(考虑下一张卡牌); 否则(是最后一张),结束回合。- 否则(这张卡牌在这一局游戏中没有发动过技能),设这张卡牌为第 \(i\) 张
1. 将其以 \(p_i\) 的概率发动技能。
2. 如果技能发动,则对敌方造成 \(d_i\) 点伤害,并结束回合。
3. 如果这张卡牌已经是最后一张(即 \(i\) 等于 \(n\)),则结束回合;否则,考虑下一张卡牌。
求你能造成的总伤害的期望。
美妙的假做法
设 \(dp_{i,j}\) 表示在前 \(i\) 轮,第 \(j\) 号牌释放过技能的概率。
设 \(f_{i,j}\) 表示在第 \(i\) 轮,前 \(j\) 号牌释放过技能的概率。
那么 \(f_{i,j}=f_{i,j-1}*(dp_{i-1,j}+(1-p_j)-dp_{i-1,j}\times(1-p_j))\),
\(dp_{i,j}=dp_{i-1,j}+(1-dp_{i-1,j})\times f_{i,j-1}\times p_j\)。
附上代码:
for(int i=1;i<=m;i++){
f[i][0]=1;
for(int j=1;j<=n;j++){
double now=(1-dp[i-1][j])*f[i][j-1]*p[j];
dp[i][j]=dp[i-1][j]+now;
f[i][j]=f[i][j-1]*(dp[i-1][j]+(1-p[j])-dp[i-1][j]*(1-p[j]));
ans+=now*a[j];
}
}
还发了一篇帖子/kk
后来一翻,这篇题解提到了这个做法,但还是不造咋错的。
这里画个图大致解释一下。
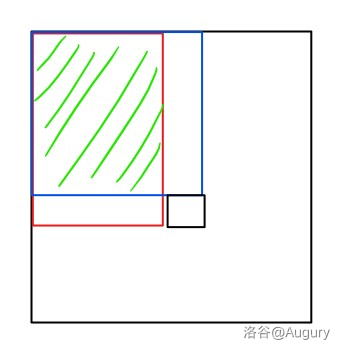
\(dp\) 值的贡献通过蓝色部分求出,\(f\) 值的贡献是通过红色部分求出。
这时,这两个值就会在绿色部分产生一些重叠,这样计算的贡献就是错误的。所以这个做法是错误的。
那为什么不特殊处理一下绿色部分呢?当然是因为我不会啦
正解
观察题解,得到一个没有重叠部分的dp。
设 \(dp_i\) 表示第 \(i\) 张牌出过的概率,那么造成伤害的期望就是 \(\sum_{i=1}^nd_i\times dp_i\)。
考虑如何求出 \(dp_i\)。
设 \(f_{i,j}\) 表示前 \(i\) 张牌中有 \(j\) 张释放过技能的概率。
为了方便转移,设 \(g_{i,j}\) 表示在 \(j\) 个可释放技能的回合中 \(i\) 没有释放过技能的概率。
显然这 \(j\) 个回合的分布不会影响 \(g\) 的取值。那么 \(g_{i,j}=(1-p_i)^j\)。
然后分两种情况讨论:
- 第 \(i\) 张牌并没有被选。根据定义,考虑从 \(f_{i-1,j}\) 转移。在此前提下,\(i\) 在可释放技能的回合中没有释放过技能。那么 \(f_{i,j}\) 就应该加上 \(f_{i-1,j}\times g_{i,m-j}\)。
- 第 \(i\) 张牌被选了。根据定义,考虑从 \(f_{i-1,j-1}\) 转移。在此前提下,\(i\) 在可释放回合中释放过技能。那么就应该加上 \(f_{i-1,j-1}\times(1-g_{i,m-(j-1)})\)。
根据定义,我们得到:\(dp_i=\sum_{i=0}^mf_{i-1,j}\times(1-g_{i,m-j})\)。
直接计算即可。
代码
void real_main(){
ans=0;
memset(dp,0,sizeof(dp));//double可以用memset赋全0,别的没试
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
n=read(),m=read();
for(int i=1;i<=n;i++)cin>>p[i]>>d[i];
for(int i=1;i<=n;i++){
g[i][0]=1;
for(int j=1;j<=m;j++)g[i][j]=g[i][j-1]*(1-p[i]);
}
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
if(j)f[i][j]+=(1-g[i][m-j+1])*f[i-1][j-1];
f[i][j]+=g[i][m-j]*f[i-1][j];
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<=min(i,m);j++){
dp[i]+=f[i-1][j]*(1.0-g[i][m-j]);
}
}
for(int i=1;i<=n;i++)ans+=dp[i]*d[i];
cout<<fixed<<setprecision(10)<<ans<<'\n';
}
signed main(){
int T=read();
while(T--)real_main();//多测
return 0;
}
P3412 仓鼠找sugar II
题意
给定一棵树,随机选择一个起点和一个终点,然后从起点开始随机游走,问走过边数量的期望。
\(n\le 10^5\)。
麻烦的做法
考虑到起点和终点一共有 \(n^2\) 种,且每种的概率相等,这不就是枚举路径嘛,鉴定为点分治。
首先定 \(1\) 号点为根,根套路,设 \(f_i\) 表示 \(i\) 走到父亲的期望步数。
然后发现不能直接把起点到 \(lca\) 路径上的 \(f\) 值全都加起来,因为正着走合反着走的期望不同。
所以,设 \(g_i\) 表示 \(i\) 的父亲走到 \(i\) 的期望步数。那么 \(s\) 到 \(t\) 的期望步数就是 \(s\) 到 \(lca\) 的路径上 \(f\) 值的和,加上 \(t\) 到 \(lca\) 路径上 \(g\) 值的和。
然后发现,这样做每次都要求一遍 \(f\) 值,这样的复杂度是 \(\Theta(n^2)\) 的。
可以用一些东西来优化成 \(\Theta(n\log n)\),但是我懒。
正解
开始之前,先考虑一下如何求出 \(f\) 和 \(g\) 的值。
不妨设 \(d_i\) 表示点 \(i\) 的度数,\(son_i\) 表示 \(i\) 的儿子组成的集合,那么根据定义:
这是非常简单的。然后考虑求出 \(g_i\):
其实这个还可以再化简。不难发现,\(f_i=d_i+\sum_{j\in son_i}f_j\),所以:
现在我们求出了 \(f\) 和 \(g\) 的值,然后考虑怎么用它。
考虑一条边会对多少个点对产生贡献。方便起见,我们枚举点 \(i(2\le i\le n)\) 到父亲的边。
然后分类讨论:
- 当起点在 \(i\) 的子树中而终点不在时,路径经过 \(i\rightarrow fa_i\)。这时会产生 \(f_i\) 的贡献。
- 当终点在 \(i\) 的子树中而起点不在时,路径经过 \(fa_i\rightarrow i\)。这时会产生 \(g_i\) 的贡献。
- 其他情况下,路径不经过这条边,不产生贡献。
容易发现,对于前两种情况,都会产生 \(siz_i\times(n-siz_i)\) 次贡献。所以答案就是:
直接计算即可,时间复杂度 \(\Theta(n)\)。
代码
void dfs1(int now,int fa){
f[now]=d[now];
siz[now]=1;
for(int nxt:tr[now]){
if(nxt==fa)continue;
dfs1(nxt,now);
f[now]+=f[nxt];
siz[now]+=siz[nxt];
}
f[now]%=mod;
}
void dfs2(int now,int fa){
if(now!=1)g[now]=(g[fa]+f[fa]-f[now]+mod)%mod;
else g[now]=0;
for(int nxt:tr[now]){
if(nxt==fa)continue;
dfs2(nxt,now);
}
}
signed main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
tr[u].push_back(v);
tr[v].push_back(u);
++d[u],++d[v];
}
dfs1(1,0);
dfs2(1,0);
for(int i=2;i<=n;i++){
ans=(ans+siz[i]*(siz[1]-siz[i])%mod*(f[i]+g[i])%mod)%mod;
}
cout<<ans*inv(n*n%mod)%mod;
return 0;
}
P3750 [六省联考 2017] 分手是祝愿
什么题目名称
题意
给定 \(n\) 个灯的初始状态,每个灯有两个状态亮和灭,通过操作第 \(i\) 个开关,所有编号为 \(i\) 的约数(包括 \(1\) 和 \(i\))的灯的状态都会被改变,即从亮变成灭,或者是从灭变成亮。
你的目标是使所有灯都灭掉。
每次你会等概率随机操作一个开关,直到所有灯都灭掉。
B 君想知道按照这个策略(也就是先随机操作,最后最小操作次数小于等于 \(k\) 步时,再使用操作次数最小的操作方法)的操作次数的期望。
求这个期望乘以 \(n\) 的阶乘对 \(100003\) 取模之后的结果。\(n\le 10^5\)。
做法
先考虑已知这些路灯的亮灭状态,如何求出最小操作次数。
不难发现,从 \(n\) 到 \(1\),有亮的就把它按掉,一定是最优的。
不妨假设当前位置为 \(i\)。
- 当 \(i=n\) 时,只能把 \(i\) 按灭掉。
- 当 \(1\le i\le n\) 时,假设 \([i+1,n]\) 都灭了。首先,更小的不能让 \(i\) 灭掉。如果试图用更大的把 \(i\) 按掉,那么就会一直需要更大的把按亮的按回去,直到没有更大的能把它按回去,这时候还是要一个一个按回去,不如直接把 \(i\) 按掉。
这样感性理解,就说明了从大到小按掉是最优的做法之一。
对于一个序列,根据刚才的过程,容易发现,需要按一下的点是固定的。因为这个操作是异或,所以顺序没有影响。
现在问题就转化成了,给定一个 \(01\) 串,每次随机选定一个位置异或 \(1\),问变成全 \(0\) 的期望步数。
然后就好做了。容易发现期望步数只与 \(1\) 的个数有关,而且最小操作次数等于 \(1\) 的数量。
不妨设 \(dp_i\) 表示从有 \(i\) 个 \(1\) 变成 \(i-1\) 个 \(1\) 的期望步数。
显然转移为:
直接转移即可。
那么步数的期望就是 \(E=\sum_{i=k+1}^{count}dp_i+k\)。\(count\) 表示初始 \(1\) 的数量。
直接计算即可,记得要乘上 \(n!\)。
代码
void update(int x){
for(int i=1;i*i<=x;i++){
if(x%i)continue;
a[i]^=1;
if(i*i!=x)a[x/i]^=1;
}
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=n;i;i--){
if(a[i]){
update(i);
++cnt;
}
}
m=min(cnt,m);
for(int i=n;i;i--)dp[i]=(n+(n-i)*dp[i+1])%mod*inv(i)%mod;
for(int i=m+1;i<=cnt;i++)ans=(ans+dp[i])%mod;
ans+=m;
for(int i=1;i<=n;i++)ans=ans*i%mod;
cout<<ans;
return 0;
}
emmm
这篇也有点长了,本地都开始卡了,后面会写个Part3,然后把链接放这。
Update 6.12:去搞具体数学了,Part3就给鸽了。这里的最后一题是原本打算放在Part3的,但是Part3被我鸽了,就搬过来了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号