[树链剖分]剖开表象看本质

本文中 \(\operatorname{LCA}(a,b)\) 指 \(a\),\(b\) 两节点的最近公共祖先

引入

考虑两个在树上的操作

1. 将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)
   这个操作很简单，用树上差分，对于节点 \(x\),\(y\),\(\operatorname{LCA}(x,y)\)进行修改 就可以在 \(\mathcal O(1)\) 内解决。
2. 求出树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和
   这个操作也很简单，先预处理出树上前缀和 \(sum\)，则 \(ans = sum_x+sum_y+sum_{\operatorname{LCA}(x,y)}\)，复杂度 \(\mathcal O (\log n)\)

但如果把两个操作结合到一起呢？

这样子就不简单了，因为如果按上述方法维护，每次2操作前都得求一遍 \(sum\)。

那，有没有可以快速维护这些操作的数据结构呢？

树链剖分

前置芝士：线段树，DFS序。

DFN

字面意思，就是DFS遍历的顺序，这里我们称其为 DFN。

比如下图这棵树，它的 DFN 长这样

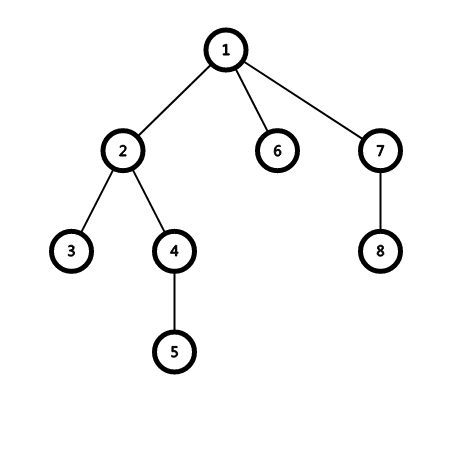
不难发现，一颗子树的所有节点的 DFN 构成一个连续的区间。

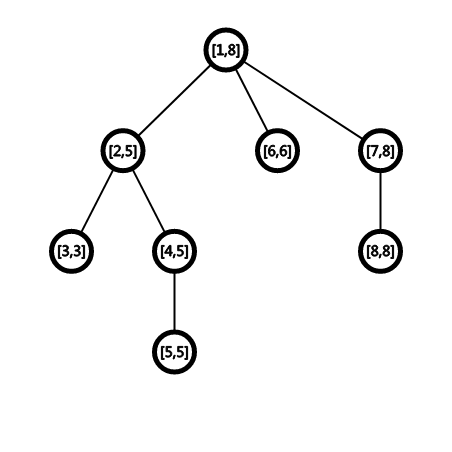
那么每个节点都对应着一段区间，就可以将类似于“把以某节点为根的子树中所有节点的值相加 \(x\)”的操作用线段树维护。

重链剖分

树链剖分分几种，其中最常用的就是重链剖分。

先弄清楚重链剖分的一些概念：

• 重儿子：子树节点最多的儿子
• 轻儿子：除重儿子其他的节点
• 重边：父亲节点和重儿子之间的边
• 轻边：父亲节点和轻儿子之间的边
• 重链：多条重边组成的链
• 轻链：多条轻边组成的链

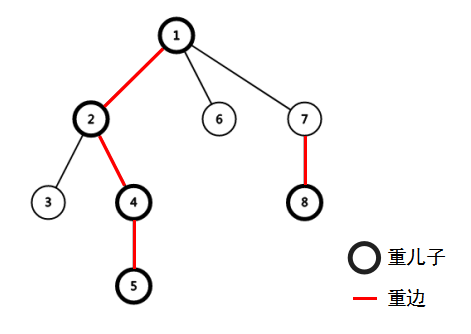
节点

为了更好地维护