[斜率优化DP]噩梦的开始
引入
我认为的斜率优化本质就是讲状态转移方程转化为 \(y=kx+b\) 的形式,并维护成一个凸包,用二分/CDQ/平衡树优化。
例1:任务安排1,2
任务安排1:LOJ 10184/Acwing300/P2365 任务安排
任务安排2:LOJ 10185/Acwing301/P5785 [SDOI2012]任务安排
两道题差不多,只是数据范围的区别,我们合在一起讲
题目大意
有 \(n\) 个任务排成一个序列,顺序不得改变,其中第 \(i\) 个任务的耗时为 \(t_i\), 费用系数为 \(c_i\)。
现需要把这 \(n\)个 任务分成若干批进行加工处理。
每批次的段头,需要额外消耗 \(S\) 的时间启动机器。每一个任务的完成时间是所在批次的结束时间。
完成一个任务的费用为:从 0 时刻到该任务所在批次结束的时间 t 乘以该任务费用系数 c。
分析
我们先列出最基本的状态转移方程。
状态表示 \(f[i,j]\):前 \(i\) 个任务,且第 \(i\) 个任务是第 \(j\) 个批次的最后一个任务的方案。
状态属性 \(f[i,j]\):方案贡献的最小值。
转移方程:
两维状态(\(i,j\))加上一个决策变量(\(k\)),时间复杂度为 \(\mathcal O (n^3)\)。
优化状态转移方程
这里,我们可以用费用提前计算的经典优化思想进行优化:
在状态转移中,我们额外引入参数 \(j\),仅仅是为了求出 \(S\) 对于当前状态的贡献。
既然是额外引入的,那就尝试把它去掉。若为 \([l,r]\) 的任务开一个新的批次,那么该批次的启动时间实际会影响的任务有 \([l,n]\)。
那么我们不妨将该段 \([l,n]\) 的 \(S\) 费用直接累加到当前状态 \(f[i]\) 上计算。
一维状态加上一个决策变量,时间复杂度为 \(\mathcal O (n^2)\)
至此,我们便可以做出任务安排1。
斜率优化
我们将式子中单独含 \(i\) 的常量提出:\(f[i]=S\times sc_n+st_i \times sc_i+\min ( f[j]-S\times sc_j-st_i \times sc_j )\)
我们知道含 \(i\) 的项是常量,所以 \(f[j]-sc_j\times(S+st_i)\) 可以转化为一下形式:
而变量1和变量2均是与 \(j\) 有关的变量,不妨令\( \begin{cases} f_j=y(j)\\ sc_j=x(j)\\ S+st_i=k\\ \end{cases} \),则该函数可转化成 \(y(j)-k\cdot x(j)\)。
求 \(y-kx(0\le j<i)\) 的极值问题,可以联想到直线的斜截式方程:\(y=kx+b\)。变形得 \(b=y-kx\)。
要求 \(y-kx(0\le j<i)\) 的极值,就是求一个点 \((x_j,y_j)\) 与当前 \(k_i\) 构成的所有直线中,截距最小的。
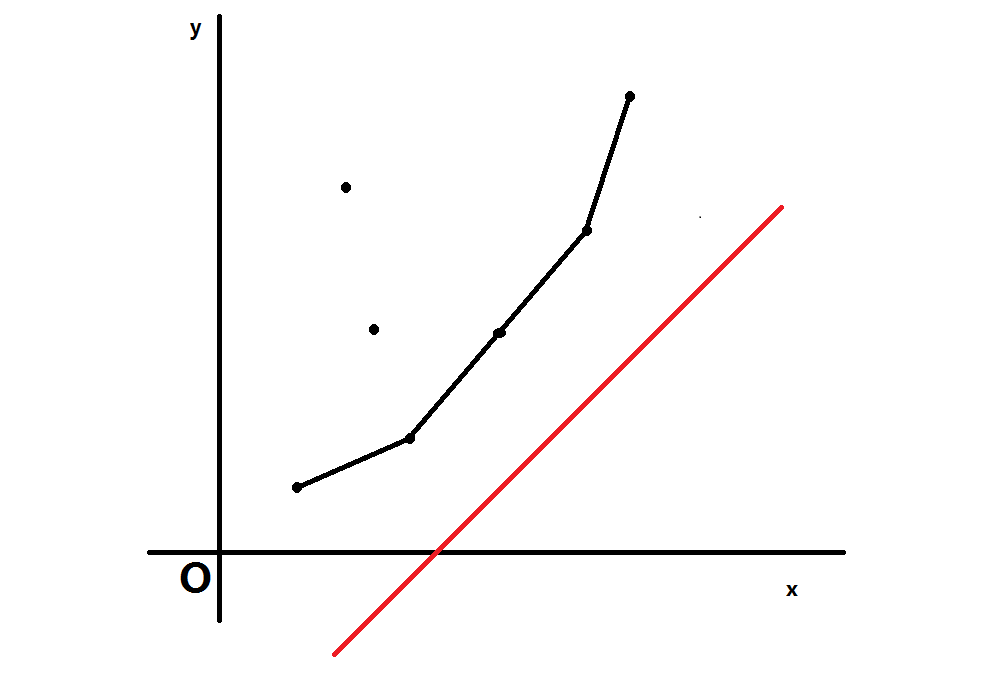
如图,黑色的点为所有 \(0\le j< i\) 的点 \((x_j,y_j)\),红色线为斜率 \(k_i\) 的某条直线。
从下往上(截距由小到大)去逼近所有的点,则第一个出现在直线上的点,就是满足 \(b_i=y_j-kx_j\) 的最小截距 \(b\)。
但暴力查找这个点最坏是 \(\mathcal O(n)\) 的,太慢。
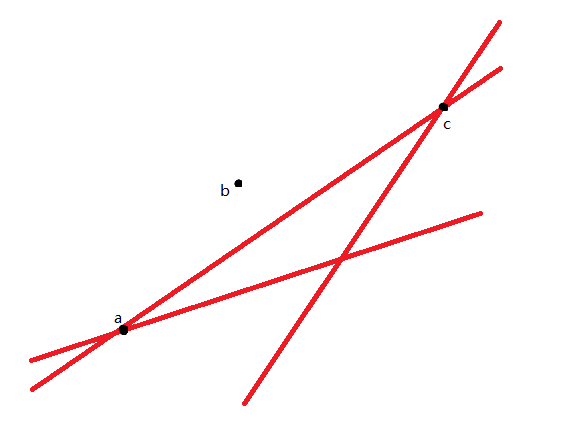
如上图,我们发现如果某个点不在凸壳上,则不可能对答案产生贡献。
对于这道题,我们需要维护下凸壳。因此,对于任意 \(f_i\),只用在下凸壳的点寻找构成直线的最小截距。
但在最坏的情况下查找还是 \(\mathcal O(n)\) 的,考虑继续优化。
由于 \(t_i,c_i\) 都是正整数,所以它们的前缀和 \(st_i,sc_i\) 一定是单调递增的。对应 \(x_j,k_i\) 也是单调递增的。
而下凸壳中相邻两点的斜率也单调递增,可得对于第一个出现在直线上的点,一定有 \(k(j-1,j)\le k_i<k(j,j+1)\)。
又由于 \(k_i\) 单调递增,所以 \(j\) 之前的点都不会是点集中第一个出现在直线上的点。
只需维护点集区间 \([j,i]\) 之间的即可,知道 \(k(j,j+1)\le k <k(j+1,j+2)\),维护区间转为 \([j+1,i]\)。
我们可以发现一个熟悉的滑动窗口模型,考虑用单调队列维护:
- 用队头的两个元素维护大于 \(k_i\) 的最小斜率 \(k(q_hh,q_{hh+1})\)。
- 插入前,保证队列中至少两个点,然后把满足 \(k(q_{tt-1},q_tt) \ge k_i\) 的点 \(q_tt\) 弹出。
这样便维护了有效下凸壳点集,时间复杂度 \(\mathcal O(n)\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e5 + 10;
int n,S,q[N];
ll t[N],c[N],f[N];
int main(){
scanf("%d%d",&n,&S);
for(int i=1;i<=n;i++){
scanf("%lld%lld",t+i,c+i);
t[i]+=t[i-1],c[i]+=c[i-1];
}
int hh=0,tt=0;q[0]=0;// 队列中第一个点是0
/*
f[i]=min(f[j]+S*(c[n]-c[j])+t[i]*(c[i]-c[j])) =>
f[i]=t[i]*c[i]+S*c[n]+min(f[j]-(S+t[i])*c[j])
y=kx+b ==> b=y-kx
f[j]-(S+t[i])*c[j]=y-kx = min(b)
k[qhh~qh+1]=y1-y2/x1-x2=(f[qh+1]-f[qhh])/(c[qh+1]-c[qhh]) > ki = t[i]+S
k[qt-1~qtt] < k[qtt~i]
*/
for(int i=1;i<=n;i++){
while(hh<tt/*至少还有两个点*/&&(f[q[hh+1]]-f[q[hh]])/*y*/<=(c[q[hh+1]]-c[q[hh]])/*x*/*(t[i]+S)/*k*/) hh++;
f[i]=f[q[hh]]+S*(c[n]-c[q[hh]])+t[i]*(c[i]-c[q[hh]]);
while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=
(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) tt--;
q[++tt]=i;
}
printf("%lld\n", f[n]);
return 0;
}
例2:任务安排3
注意到此题与前两道题唯一的差别便是 \(t_i\) 不一定是正整数,即 \(st_i\) 不一定单调递增。
这意味着我们要将下凸壳中的所有点保存下来,不因为 \(k_i\) 出队。查找时二分答案,总时间复杂度为 \(\mathcal O (n\log n)\)。
代码就不贴了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号