|
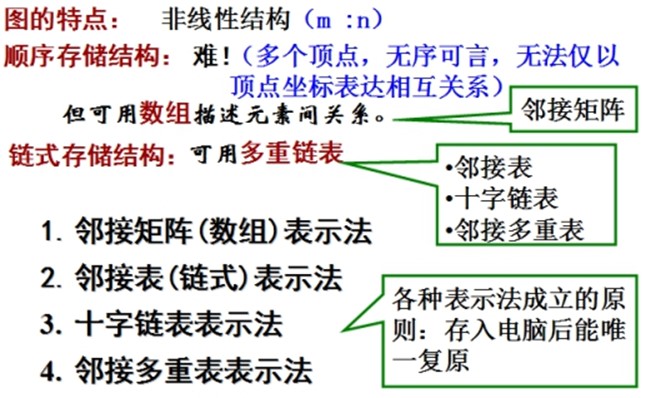
① //图的数组 (邻接矩阵 ) 存储结构----有向图, 无向图, 网 |
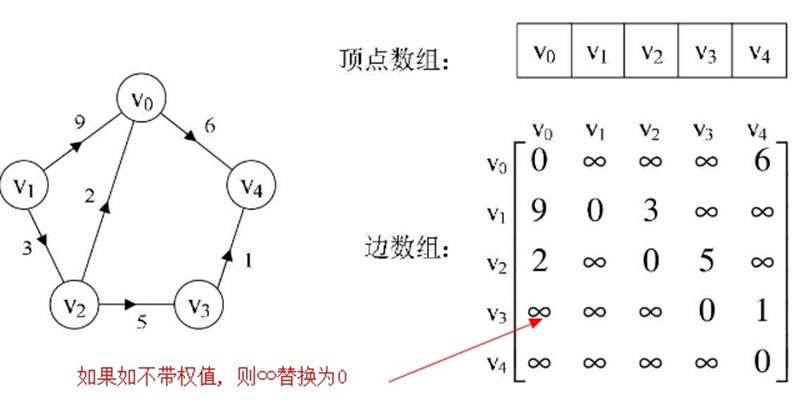
思路: 用两个数组来表示图 ① 一个一维数组存储图中顶点信息; ② 一个二维数组(称为邻接矩阵----是一个对称矩阵,矩阵的元满足aij=aji)存储图中的边或弧的信息。 |
//起始部分 #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXVEX 100 /* 最大顶点数,应由用户定义 */ #define INFINITY 65535 |
//用顶点数组和边数组(邻接矩阵)定义表结构 |
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表, 这里用edge这个标识符更准确 */ int numNodes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; |
/* 建立无向网图的邻接矩阵表示 */ |
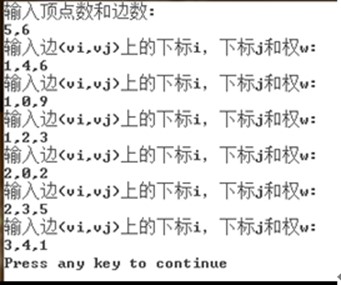
void CreateMGraph(MGraph *G) { int i,j,k,w; printf("输入顶点数和边数:\n"); scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */ for(i = 0;i <G->numNodes;i++) /* 读入顶点信息,建立顶点表 */ scanf(&G->vexs[i]); for(i = 0;i <G->numNodes;i++) for(j = 0;j <G->numNodes;j++) G->arc[i][j]=INFINITY; /* 邻接矩阵初始化 */ for(k = 0;k <G->numEdges;k++) /* 读入numEdges条边,建立邻接矩阵 */ { printf("输入边(vi,vj)上的下标i,下标j和权w:\n"); scanf("%d,%d,%d",&i,&j,&w); /* 输入边(vi,vj)上的权w */ G->arc[i][j]=w; G->arc[j][i]= G->arc[i][j]; /* 因为是无向图,矩阵对称 */ } } |
//主函数 |
int main(void) { MGraph Graph; CreateMGraph(&Graph);
return 0; }
对于有向图, 我们要先检索邻接矩阵的行, 再检索列; 对于无向图, 先检索行或列都可以. |
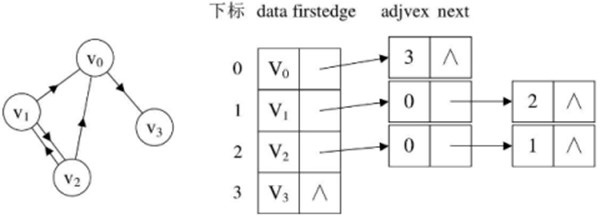
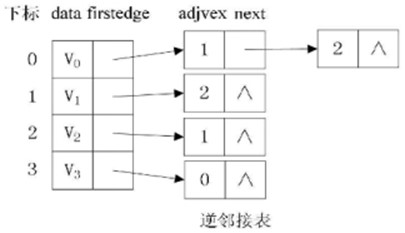
② //邻接表----有向图, 无向图, 网 |
//思路: ① 顶点用一维数组来储存存储数组, 这个数组是一个结构体数组, 每个结构体数组的分量包括顶点的数据(data)和边表头结点的指针(firstedge), 指向该顶点的第一个邻接点; ② 图中每个顶点的所有邻接点构成一个链表, 边界结点
※ 邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。 |
//邻接表&逆邻接表 邻接表: 把顶点当弧尾(确定顶点的出度)
逆邻接表: 把顶点当弧头(确定顶点的入度)
|
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXVEX 100 /* 最大顶点数,应由用户定义 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ |
/* 边 表 结点 */ |
typedef struct EdgeNode { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ EdgeType info; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; |
/* 顶点 表 结点 */ |
typedef struct VertexNode { VertexType data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; |
//整个邻接表 |
typedef struct { AdjList adjList; int numNodes,numEdges; /* 图中当前顶点数和边数 */ }GraphAdjList; |
/* 建立图的邻接表结构 */ |
void CreateALGraph(GraphAdjList *G) { int i,j,k; EdgeNode *e; printf("输入顶点数和边数:\n"); scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */ for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */ { scanf(&G->adjList[i].data); /* 输入顶点信息 */ G->adjList[i].firstedge=NULL; /* 将边表置为空表 */ }
for(k = 0;k < G->numEdges;k++)/* 建立边表 */ { printf("输入边(vi,vj)上的顶点序号:\n"); scanf("%d,%d",&i,&j); /* 输入边(vi,vj)上的顶点序号 */ e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */ e->adjvex=j; /* 邻接序号为j */ e->next=G->adjList[i].firstedge; /* 将e的指针指向当前顶点上指向的结点 */ G->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */
e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */ e->adjvex=i; /* 邻接序号为i */ e->next=G->adjList[j].firstedge; /* 将e的指针指向当前顶点上指向的结点 */ G->adjList[j].firstedge=e; /* 将当前顶点的指针指向e */ } } |
//主函数 |
int main(void) { GraphAdjList Graph; CreateALGraph(&Graph);
return 0; } |
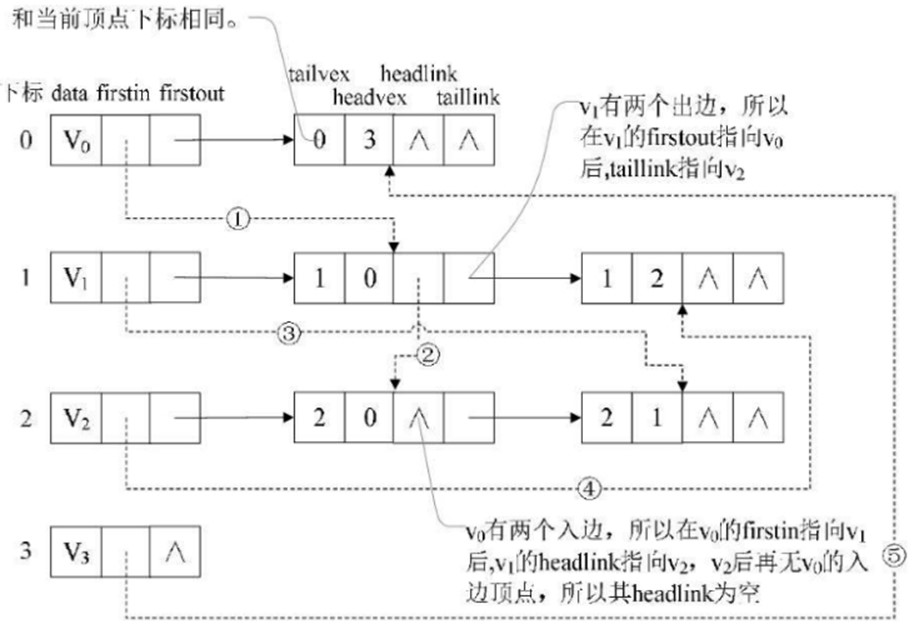
③ //十字链表----有向图: 结合邻接表和逆邻接表 |
(重新定义顶点表结点结构和边表结点结构) (1)顶点表结点,设3个域(每个顶点也是一个数据元素)
data: 顶点信息 firstin: 以该顶点为弧头的第一条弧结点 firstout: 以该顶点为弧尾的第一条弧结点
(2)边表结点,设5个域(每段弧是一个数据元素)
tailvex: 弧尾顶点位置 headvex: 弧头顶点位置 hlink: 指向和这条弧的弧头相同的下一条弧的位置 tlink: 指向和这条弧的弧尾相同的下一弧弧的位置 info: 弧信息
|
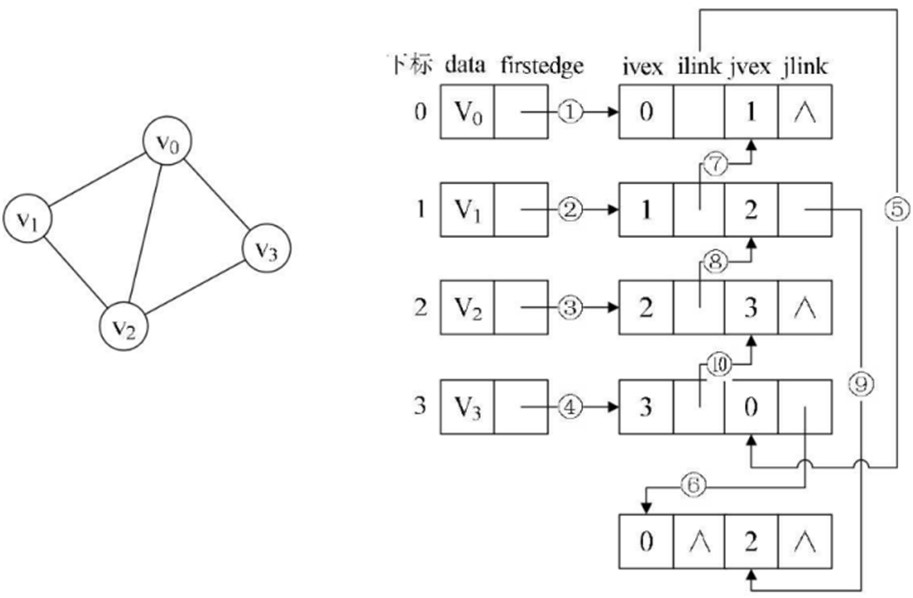
④ //邻接多重表----无向图 |
(1)顶点表结点
data: 存储顶点信息 firstedge: 指向依附于该顶点的第一条边结点
(2)边表结点
mark: 标志域,标记该边是否被搜索过。 ivex, jvex : 该边依附的两个顶点的位置 ilink: 指向下一条依附顶点 ivex 的边 Jlink: 指向下一条依附顶点 jvex 的边 info: 边信息
|
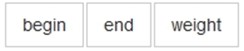
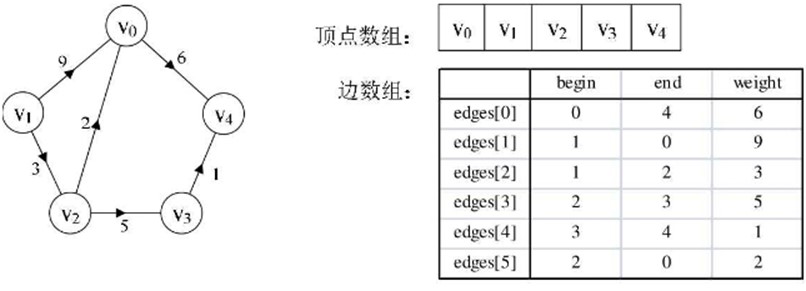
⑤ //边集数组----有向图 边集数组是由两个一维数组构成。一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成. 边数组
|
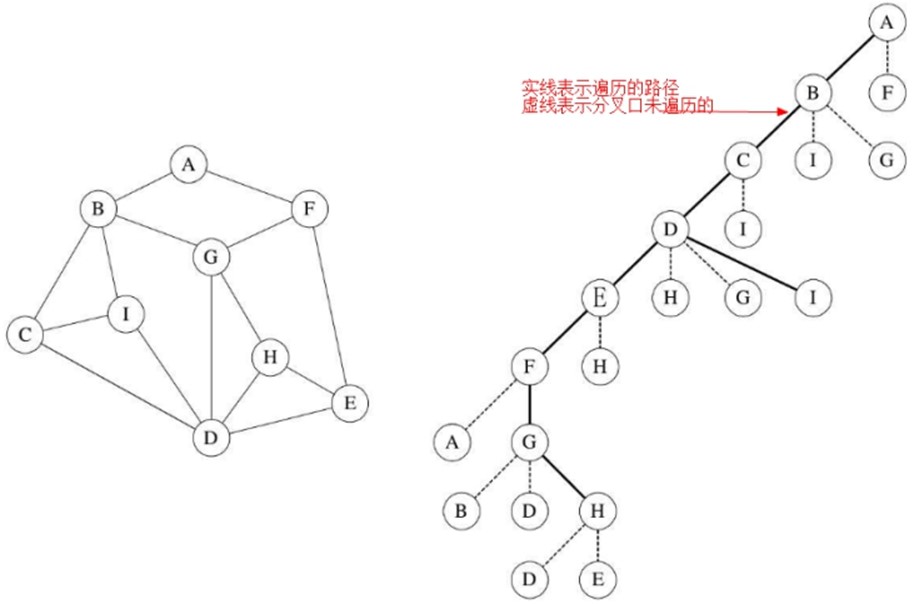
找钥匙: ①从任意一个房间开始, 翻个底朝天; ②换到下一间, 再翻个底朝天...... 右手原则: 在没有碰到重复顶点的情况下, 分叉路口始终是向右手边走.(当然也可以遵循"左手原则"来遍历)
|
找钥匙: ①查看所有房间里最显眼的位置; ②查看所有房间里此显眼的位置...... (深度优先遍历和广度优先遍历的路径都不唯一) |
|
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITY 65535 |
//图的结构定义----用邻接矩阵 |
typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; |
/* 用到的队列结构与函数 */ /* 循环队列的顺序存储结构 */ |
typedef struct { int data[MAXSIZE]; int front; /* 队头指针 */ int rear; /* */ }Queue; |
/* 初始化一个空队列Q */ |
Status InitQueue(Queue *Q) { Q->front=0; Q->rear=0; return OK; } |
/* 若队列Q为空队列,则返回TRUE,否则返回FALSE */ |
Status QueueEmpty(Queue Q) { if(Q.front==Q.rear) /* 队列空的标志 */ return TRUE; else return FALSE; } |
/* 若队列未满,则插入元素e为Q新的队尾元素 */ |
Status EnQueue(Queue *Q,int e) { if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */ return ERROR; Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */ Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } |
/* 若队列不空,则删除Q中队头元素,用e返回其值 */ |
Status DeQueue(Queue *Q,int *e) { if (Q->front == Q->rear) /* 队列空的判断 */ return ERROR; *e=Q->data[Q->front]; /* 将队头元素赋值给e */ Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } |
//创建图的函数 |
void CreateMGraph(MGraph *G) { int i, j;
G->numEdges=15; G->numVertexes=9;
/* 读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I';
/* 初始化图, 一行一行地将各元素初始化为0 */ for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } }
//将结点之间有边的数组元素重新赋值, 下面构造的是对称矩阵的左半部分 G->arc[0][1]=1; G->arc[0][5]=1;
G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1;
G->arc[2][3]=1; G->arc[2][8]=1;
G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1;
G->arc[4][5]=1; G->arc[4][7]=1;
G->arc[5][6]=1;
G->arc[6][7]=1;
//下面的操作是为了形成一个对称矩阵, 下面构造的是对称矩阵的右半部分 for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* 邻接矩阵的深度优先递归算法 */ |
Boolean visited[MAXVEX]; /* 访问标志的数组, 类型为Boolean, 包括TRUE和FALSE两个值 */
void DFS(MGraph G, int i) //DFS会被自身和DFSTraverse()函数调用, i是遍历开始的顶点序号 { visited[i] = TRUE; //说明当前顶点已被访问 printf("%c ", G.vexs[i]);/* 打印顶点,也可以是其它操作 */ int j; for(j = 0; j < G.numVertexes; j++) if(G.arc[i][j] == 1 && !visited[j]) // visited[j]==0 DFS(G, j);/* 对为访问的邻接顶点递归调用 */ } //在本程序中, 会先执行下面的DFSTraverse()函数, 此时i=0, 然后DFSTraverse()函数会调用DFS()函数, 此时, 从0号顶点开始遍历, 然后DFS会递归调用自身, 每遍历一个顶点, visited[i] = TRUE;这一句都会执行, 表明该顶点已被访问. |
/* 邻接矩阵的深度遍历操作 */ |
void DFSTraverse(MGraph G) { int i; for(i = 0; i < G.numVertexes; i++) visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */ for(i = 0; i < G.numVertexes; i++) if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ DFS(G, i); } |
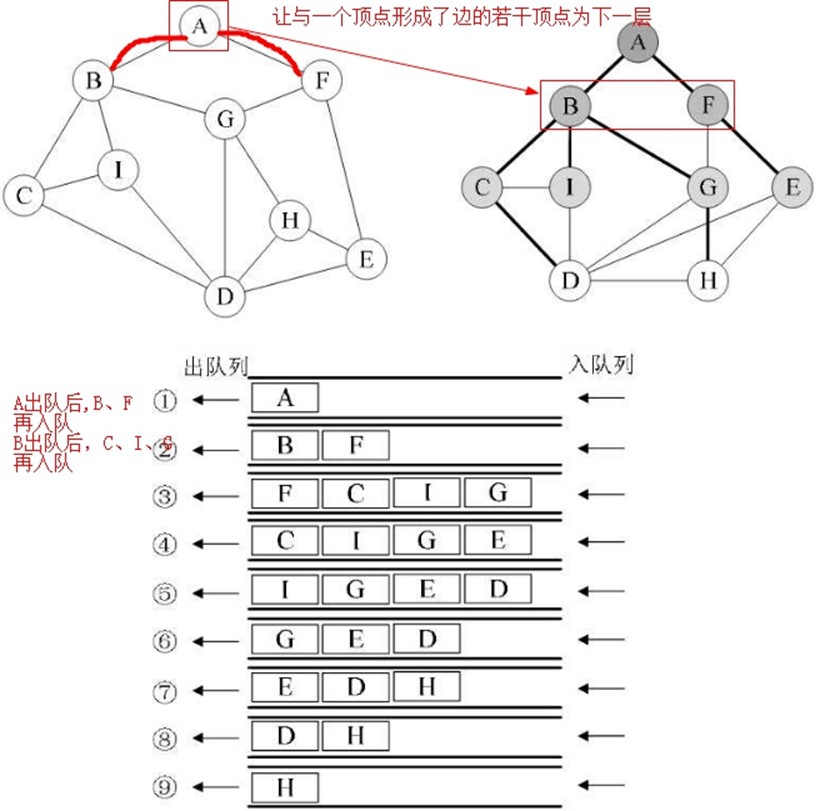
/* 邻接矩阵的广度遍历算法 */ |
void BFSTraverse(MGraph G) { int i, j; Queue Q; for(i = 0; i < G.numVertexes; i++) visited[i] = FALSE; InitQueue(&Q); /* 初始化一辅助用的队列 */ for(i = 0; i < G.numVertexes; i++) /* 对每一个顶点做循环 */ { if (!visited[i]) /* 若是未访问过就处理 */ { visited[i]=TRUE; /* 设置当前顶点访问过 */ printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */ EnQueue(&Q,i); /* 将此顶点入队列 */ while(!QueueEmpty(Q)) /* 若当前队列不为空 */ { DeQueue(&Q,&i); /* 将队对元素出队列,赋值给i */ for(j=0;j<G.numVertexes;j++) { /* 判断其它顶点若与当前顶点存在边且未访问过 */ if(G.arc[i][j] == 1 && !visited[j]) //如果 G.arc[i][j]这条边存在 { visited[j]=TRUE; /* 将找到的此顶点标记为已访问 */ printf("%c ", G.vexs[j]); /* 打印顶点 */ EnQueue(&Q,j); /* 将找到的此顶点入队列 */ } } } } } } |
//主函数 |
int main(void) { MGraph Graph; CreateMGraph(&Graph); printf("\n深度遍历:"); DFSTraverse(Graph); printf("\n广度遍历:"); BFSTraverse(Graph); return 0; }
|
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ |
/* 邻接矩阵结构 */ |
typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; |
/* 邻接表结构 */ |
typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; |
/* 顶点表结点 */ |
typedef struct VertexNode { int in; /* 顶点入度 */ char data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; |
/* 边表结点 */ |
typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; /* **************************** */ |
/* 用到的队列结构与函数 */ /* 循环队列的顺序存储结构 */ |
typedef struct { int data[MAXSIZE]; int front; /* 头指针 */ int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */ }Queue; |
/* 初始化一个空队列Q */ |
Status InitQueue(Queue *Q) { Q->front=0; Q->rear=0; return OK; } |
/* 若队列Q为空队列,则返回TRUE,否则返回FALSE */ |
Status QueueEmpty(Queue Q) { if(Q.front==Q.rear) /* 队列空的标志 */ return TRUE; else return FALSE; } |
/* 若队列未满,则插入元素e为Q新的队尾元素 */ |
Status EnQueue(Queue *Q,int e) { if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */ return ERROR; Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */ Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } |
/* 若队列不空,则删除Q中队头元素,用e返回其值 */ |
Status DeQueue(Queue *Q,int *e) { if (Q->front == Q->rear) /* 队列空的判断 */ return ERROR; *e=Q->data[Q->front]; /* 将队头元素赋值给e */ Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } |
//创建图的函数 |
void CreateMGraph(MGraph *G) { int i, j;
G->numEdges=15; G->numVertexes=9;
/* 读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I';
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } }
G->arc[0][1]=1; G->arc[0][5]=1;
G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1;
G->arc[2][3]=1; G->arc[2][8]=1;
G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1;
G->arc[4][5]=1; G->arc[4][7]=1;
G->arc[5][6]=1;
G->arc[6][7]=1;
for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* 利用邻接矩阵构建邻接表 */ |
void CreateALGraph(MGraph G,GraphAdjList *GL) { int i,j; EdgeNode *e;
*GL = (GraphAdjList)malloc(sizeof(graphAdjList));
(*GL)->numVertexes=G.numVertexes; (*GL)->numEdges=G.numEdges; for(i= 0;i <G.numVertexes;i++) /* 读入顶点信息,建立顶点表 */ { (*GL)->adjList[i].in=0; (*GL)->adjList[i].data=G.vexs[i]; (*GL)->adjList[i].firstedge=NULL; /* 将边表置为空表 */ }
for(i=0;i<G.numVertexes;i++) /* 建立边表 */ { for(j=0;j<G.numVertexes;j++) { if (G.arc[i][j]==1) { e=(EdgeNode *)malloc(sizeof(EdgeNode)); e->adjvex=j; /* 邻接序号为j */ e->next=(*GL)->adjList[i].firstedge; /* 将当前顶点上的指向的结点指针赋值给e */ (*GL)->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */ (*GL)->adjList[j].in++;
} } }
} |
/* 邻接表的深度优先递归算法 */ |
Boolean visited[MAXSIZE]; /* 访问标志的数组 */
void DFS(GraphAdjList GL, int i) { visited[i] = TRUE; printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */ EdgeNode *p; p = GL->adjList[i].firstedge; while(p) // while(p!=0) { if(!visited[p->adjvex]) DFS(GL, p->adjvex);/* 对为访问的邻接顶点递归调用 */ p = p->next; } } |
/* 邻接表的深度遍历操作 */ |
void DFSTraverse(GraphAdjList GL) { int i; for(i = 0; i < GL->numVertexes; i++) visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */ for(i = 0; i < GL->numVertexes; i++) if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ DFS(GL, i); } |
/* 邻接表的广度遍历算法 */ |
void BFSTraverse(GraphAdjList GL) { int i; EdgeNode *p; Queue Q; for(i = 0; i < GL->numVertexes; i++) visited[i] = FALSE; InitQueue(&Q); for(i = 0; i < GL->numVertexes; i++) { if (!visited[i]) { visited[i]=TRUE; printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */ EnQueue(&Q,i); while(!QueueEmpty(Q)) { DeQueue(&Q,&i); p = GL->adjList[i].firstedge; /* 找到当前顶点的边表链表头指针 */ while(p) { if(!visited[p->adjvex]) /* 若此顶点未被访问 */ { visited[p->adjvex]=TRUE; printf("%c ",GL->adjList[p->adjvex].data); EnQueue(&Q,p->adjvex); /* 将此顶点入队列 */ } p = p->next; /* 指针指向下一个邻接点 */ } } } } } |
//主函数 |
int main(void) { MGraph Graph; GraphAdjList GL; CreateMGraph(&Graph); CreateALGraph(Graph,&GL);
printf("\n深度遍历:"); DFSTraverse(GL); printf("\n广度遍历:"); BFSTraverse(GL); return 0; }
|
Prim算法特点(对顶点操作): 顶点归并,与边数无关,适于稠密网。 普里姆算法的基本思想: 在生成树的构造过程中,图中 n 个顶点分属两个集合:已落在生成树上的顶点集 U (其序号为下面代码中的数组int adjvex[MAXVEX]的元素)和尚未落在生成树上的顶点集V-U ,则应在所有连通U中的顶点和V-U中的顶点的边中选取权值最小的边(该边的权值为下面代码中的数组int lowcost[MAXVEX]的元素)。 步骤: 设N=(V,{E})是连通网,TE是N上最小生成树中边的集合: (1)初始令U={u0},(u0属于V), TE=NULL (2)在所有u属于U,v属于V-U的边(u,v)属于E中,找一条代价最小的边(u0,v0) (3)将(u0,v0)并入集合TE,同时v0并入U (4)重复上述操作直至U=V为止,则T=(V,{TE})为N的最小生成树
|
① 初始化两个数组,一个用来存放边的起始点,一个用于存放边权值 ② 赋初值,从0开始,所有边的权值都和v0相关,所有边权值的起始点都是v0 ③.大循环1到MG.numVertexes-1次 ④ 遍历边权值数组,找当前数组中的最小值,并将发现的能构成最小权值的顶点的下标存入k, 以待使用 ⑤ 打印边 ⑥ 将加入的顶点的lowcost设置为0 ⑦ 使用新加入的顶点的邻接矩阵来更新lowcost数组和adjvex数组 //起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ |
//图的结构定义 |
typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j;
/* printf("请输入边数和顶点数:"); */ G->numEdges=15; G->numVertexes=9;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } }
G->arc[0][1]=10; G->arc[0][5]=11; G->arc[1][2]=18; G->arc[1][8]=12; G->arc[1][6]=16; G->arc[2][8]=8; G->arc[2][3]=22; G->arc[3][8]=21; G->arc[3][6]=24; G->arc[3][7]=16; G->arc[3][4]=20; G->arc[4][7]=7; G->arc[4][5]=26; G->arc[5][6]=17; G->arc[6][7]=19;
for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* Prim算法生成最小生成树 */ |
void MiniSpanTree_Prim(MGraph G) { int min, i, j, k; int adjvex[MAXVEX]; /*已落在生成树上的顶点集 U中各顶点的序号 */ int lowcost[MAXVEX];/*所有连通U中的顶点和V-U中的顶点的边中选取权值最小的边的权值*/
adjvex[0] = 0; /* 初始化第一个顶点下标为0 */ lowcost[0] = 0; /* lowcost的值为0, 因为一个顶点到其自身的权值为0 */
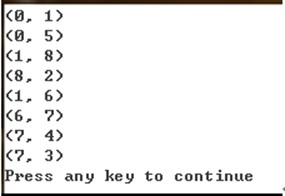
for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0以外的全部顶点 */ { adjvex[i] = 0; /* 暂时将U中各顶点的序号初始化为0 */ lowcost[i] = G.arc[0][i]; /* 将邻接矩阵第0行所有权值先加入数组 */ } for(i = 1; i < G.numVertexes; i++) //注意, 下面有两个内循环 { min = INFINITY; /*初始化最小权值为∞, 通常设置为不可能的大数字如32767、65535等 */ j = 1; k = 0; while(j < G.numVertexes) /* 循环全部顶点 */ {//找出lowcost数组已存储的最小权值 if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */ { min = lowcost[j]; /* 则让当前权值成为最小值 */ k = j; /* 将发现的能构成最小权值的顶点的下标存入k, 以待使用 */ } j++; } printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */ lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
for(j = 1; j < G.numVertexes; j++) /* 循环所有顶点 */ { if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) {/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树之前的权值 */ lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */ adjvex[j] = k; /* 将下标为k的顶点存入adjvex */ } } } } |
//主函数 |
int main(void) { MGraph G; CreateMGraph(&G); MiniSpanTree_Prim(G);
return 0; }
|
我们也可以设置一个辅助的结构体数组closedge: struct { VertexType adjvex; // 已落在生成树上的顶点集 U中各顶点的序号 VRType lowcost; // 所有连通U中的顶点和V-U中的顶点的边中选取权值最小的边的权值 } closedge[MAX_VERTEX_NUM]; |
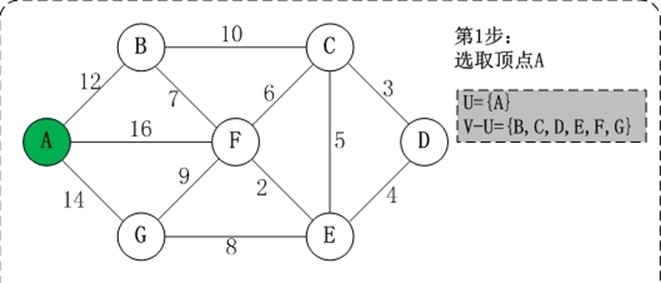
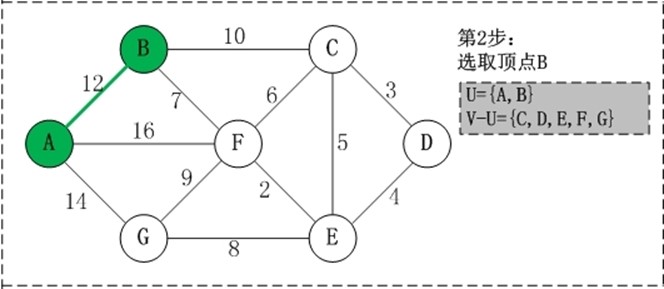
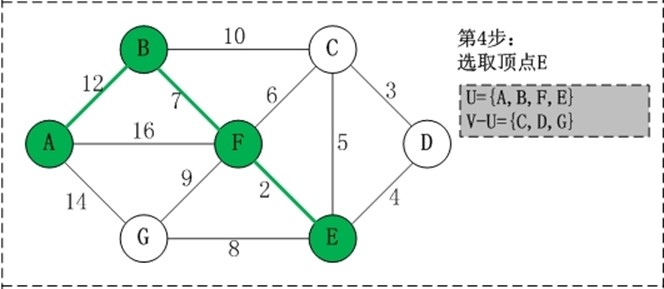
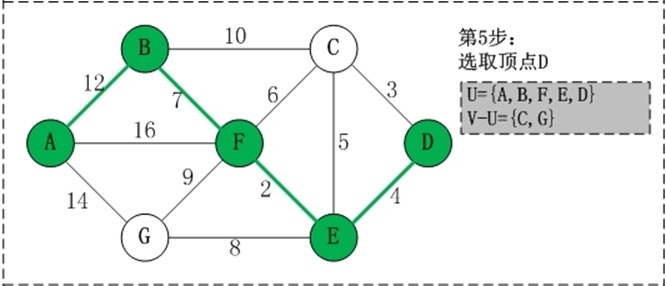
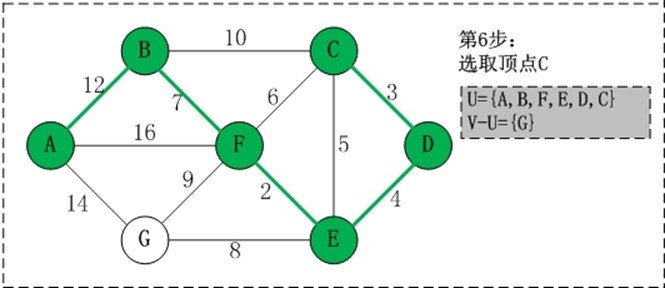
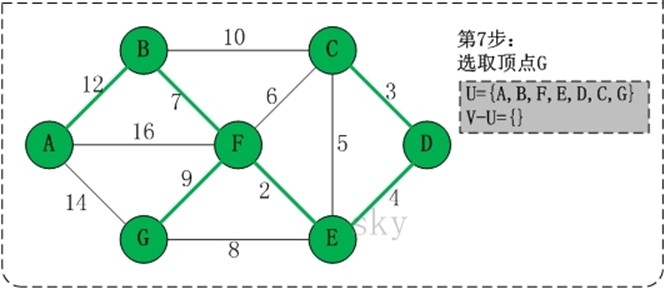
初始状态:V是所有顶点的集合,即V={A,B,C,D,E,F,G};U和T都是空! 第1步:将顶点A加入到U中。 此时,U={A}。 第2步:将顶点B加入到U中。 上一步操作之后,U={A}, V-U={B,C,D,E,F,G};因此,边(A,B)的权值最小。将顶点B添加到U中;此时,U={A,B}。 第3步:将顶点F加入到U中。 上一步操作之后,U={A,B}, V-U={C,D,E,F,G};因此,边(B,F)的权值最小。将顶点F添加到U中;此时,U={A,B,F}。 第4步:将顶点E加入到U中。 上一步操作之后,U={A,B,F}, V-U={C,D,E,G};因此,边(F,E)的权值最小。将顶点E添加到U中;此时,U={A,B,F,E}。 第5步:将顶点D加入到U中。 上一步操作之后,U={A,B,F,E}, V-U={C,D,G};因此,边(E,D)的权值最小。将顶点D添加到U中;此时,U={A,B,F,E,D}。 第6步:将顶点C加入到U中。 上一步操作之后,U={A,B,F,E,D}, V-U={C,G};因此,边(D,C)的权值最小。将顶点C添加到U中;此时,U={A,B,F,E,D,C}。 第7步:将顶点G加入到U中。 上一步操作之后,U={A,B,F,E,D,C}, V-U={G};因此,边(F,G)的权值最小。将顶点G添加到U中;此时,U=V。
此时,最小生成树构造完成!它包括的顶点依次是:A B F E D C G。 |
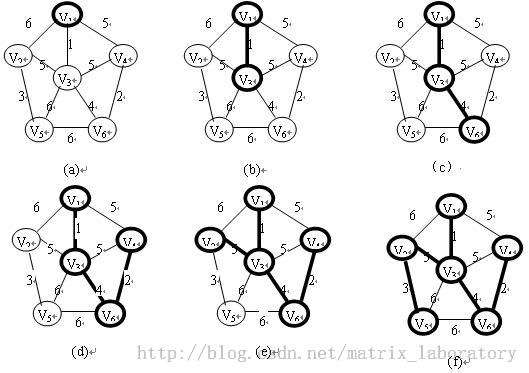
Kruskal算法特点(对边操作):边归并,适于求稀疏网。 克鲁斯卡尔算法的基本思想: 考虑问题的出发点: 为使生成树上边的权值之和达到最小,则应使生成树中每一条边的权值尽可能地小。 可以看出Kruskal算法属于一种贪心算法,而且能保证找到全局最优解。 步骤: 设连通网N=(V,{E}),令最小生成树 (1)初始状态为只有n个顶点而无边的非连通图T=(V,{NULL})--森林,每个顶点自成一个连通分量 (2)在E中选取代价最小的边,若该边的两个顶点不在同一个图中(即没有形成回路),则将此边加入到T中;否则,舍去此边,选取下一条代价最小的边 (3)依此类推,直至T中所有顶点都在同一连通分量上为止
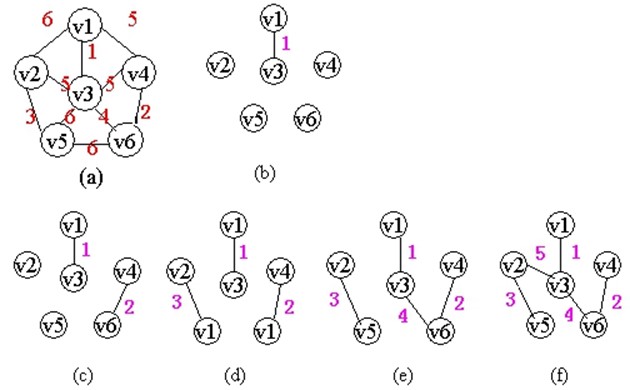
图中先将每个顶点看作独立的子图,然后查找最小权值边,这条边是有限制条件的,边的两个顶点必须不在同一个图中(否则形成回路, 这就不是连通图的极小连通子图(即生成树)了.),如上图,第一个图中找到最小权值边为(v1,v3),且满足限制条件,继续查找到边(v4,v6),(v2,v5),(v3,v6),当查找到最后一条边时,仅仅只有(v2,v3)满足限制条件,其他的如(v3,v4),(v1,v4)都在一个子图里面,不满足条件,至此已经找到最小生成树的所有边。
|
① 定义一个边集,一个顶点集, 边集按照权的大小排列,将结点集全部初始化为0 ② 循环边集中的每一条边, 用定义的Find()函数检查每条边的起点和终点能走到的最远的结点在哪里,如果相同就继续循环,否则打印并修改parent数组
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
#define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535 |
//图的结构 |
typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; |
/* 对边集数组Edge结构的定义 */ |
typedef struct { int begin; int end; int weight; }Edge; |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j;
/* printf("请输入边数和顶点数:"); */ G->numEdges=15; G->numVertexes=9;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } }
G->arc[0][1]=10; G->arc[0][5]=11; G->arc[1][2]=18; G->arc[1][8]=12; G->arc[1][6]=16; G->arc[2][8]=8; G->arc[2][3]=22; G->arc[3][8]=21; G->arc[3][6]=24; G->arc[3][7]=16; G->arc[3][4]=20; G->arc[4][7]=7; G->arc[4][5]=26; G->arc[5][6]=17; G->arc[6][7]=19;
for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* 交换权值 以及头和尾 */ |
void Swapn(Edge *edges,int i, int j) { int temp; temp = edges[i].begin; edges[i].begin = edges[j].begin; edges[j].begin = temp; temp = edges[i].end; edges[i].end = edges[j].end; edges[j].end = temp; temp = edges[i].weight; edges[i].weight = edges[j].weight; edges[j].weight = temp; } |
/* 对权值进行排序 */ |
void sort(Edge edges[],MGraph *G) { int i, j; for ( i = 0; i < G->numEdges; i++) { for ( j = i + 1; j < G->numEdges; j++) { if (edges[i].weight > edges[j].weight) { Swapn(edges, i, j); } } } printf("权排序之后的为:\n"); for (i = 0; i < G->numEdges; i++) { printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); }
} |
/* 查找连线顶点的尾部下标 */ |
int Find(int *parent, int f) //查找从f这个顶点开始能走到的最远的顶点是哪里 {//如果最后走到的最远的顶点相同,说明是有环路生成的 while ( parent[f] > 0) { f = parent[f]; } return f; } |
/* 生成最小生成树 */ |
void MiniSpanTree_Kruskal(MGraph G) { int i, j, n, m; int k = 0;
Edge edges[MAXEDGE];/* 定义边集数组, 它是一个结构体数组*/ int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */
/* 用来构建边集数组并排序********************* */ for ( i = 0; i < G.numVertexes-1; i++) { for (j = i + 1; j < G.numVertexes; j++) { if (G.arc[i][j]<INFINITY) { edges[k].begin = i; edges[k].end = j; edges[k].weight = G.arc[i][j]; k++; } } } sort(edges, &G); /* ******************************************* */
for (i = 0; i < G.numVertexes; i++) parent[i] = 0; /* 初始化数组值为0 */
printf("打印最小生成树:\n"); for (i = 0; i < G.numEdges; i++) /* 循环每一条边 */ { n = Find(parent,edges[i].begin); m = Find(parent,edges[i].end); if (n != m) /* 假如n与m不等,说明此边没有与现有的生成树形成环路 */ { parent[n] = m; // parent数组下标记录了边起点,数组元素记录了边终点 printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); } } } |
//主函数 |
int main(void) { MGraph G; CreateMGraph(&G); MiniSpanTree_Kruskal(G); return 0; }
|
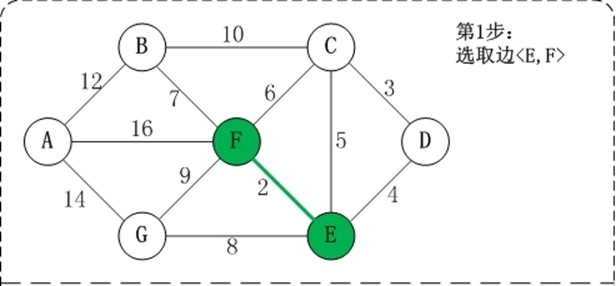
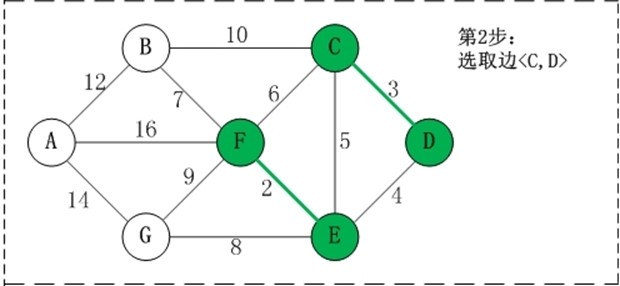
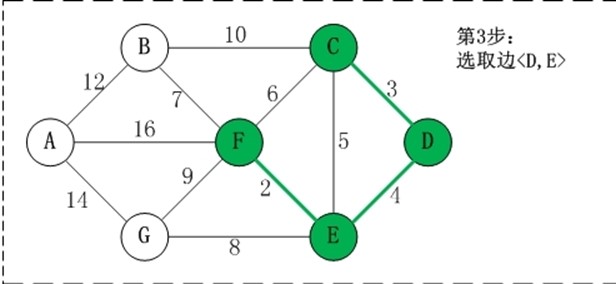
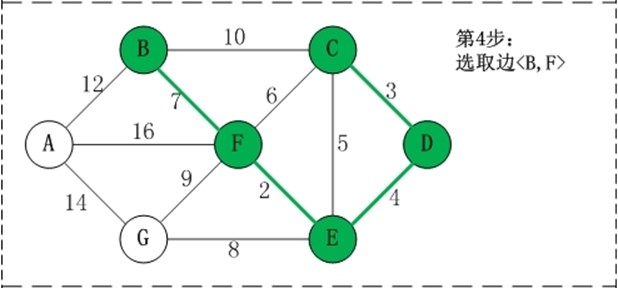
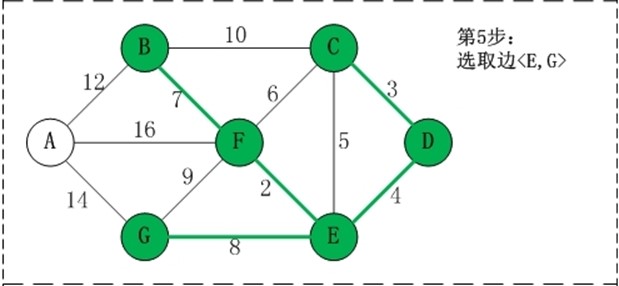
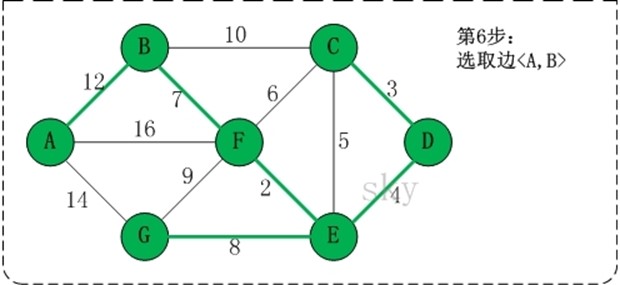
用数组R保存最小生成树结果
第1步:将边<E,F>加入R中。 边<E,F>的权值最小,因此将它加入到最小生成树结果R中。 第2步:将边<C,D>加入R中。 上一步操作之后,边<C,D>的权值最小,因此将它加入到最小生成树结果R中。 第3步:将边<D,E>加入R中。 上一步操作之后,边<D,E>的权值最小,因此将它加入到最小生成树结果R中。 第4步:将边<B,F>加入R中。 上一步操作之后,边<C,E>的权值最小,但<C,E>会和已有的边构成回路;因此,跳过边<C,E>。同理,跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。 第5步:将边<E,G>加入R中。 上一步操作之后,边<E,G>的权值最小,因此将它加入到最小生成树结果R中。 第6步:将边<A,B>加入R中。 上一步操作之后,边<F,G>的权值最小,但<F,G>会和已有的边构成回路;因此,跳过边<F,G>。同理,跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。
此时,最小生成树构造完成!它包括的边依次是:<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。 |
单源最短路径(一顶点到其余各顶点)——用Dijkstra(迪杰斯特拉)算法 所有顶点间的最短路径(任意两顶点之间)——用Floyd(弗洛伊德)算法 |
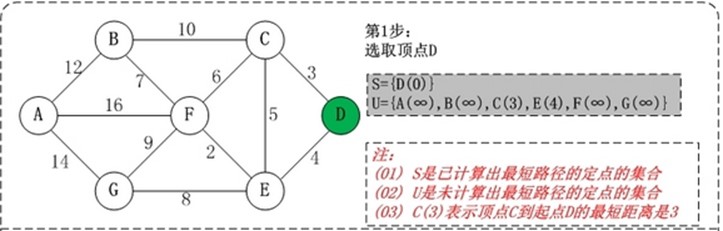
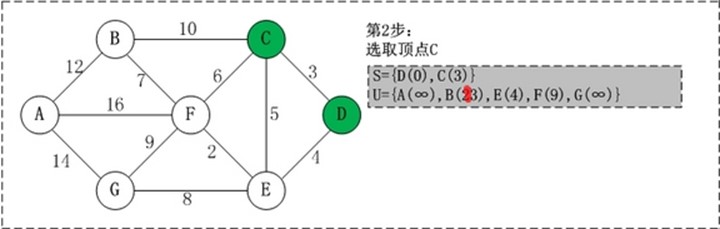
步骤: (1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。 (2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。 (3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。 (4) 重复步骤(2)和(3),直到遍历完所有顶点。
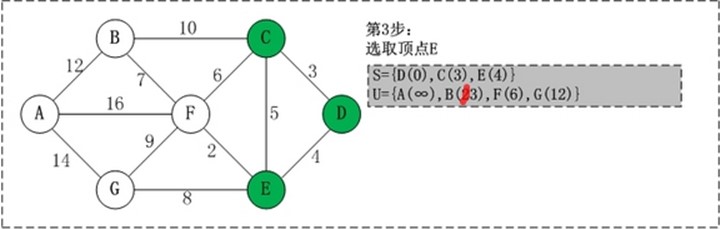
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合! 第1步:将顶点D加入到S中。 此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。 第2步:将顶点C加入到S中。 上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。 此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。 第3步:将顶点E加入到S中。 上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。 此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。 第4步:将顶点F加入到S中。 此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
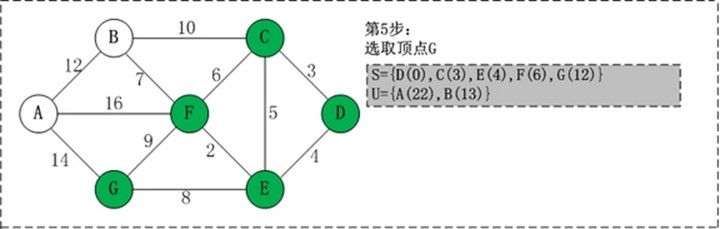
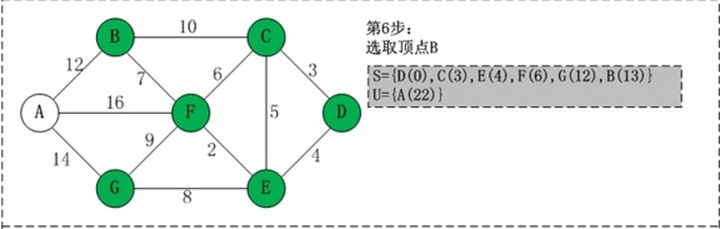
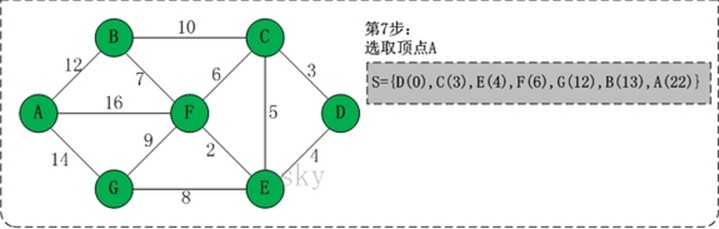
第5步:将顶点G加入到S中。 此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。 第6步:将顶点B加入到S中。 此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。 第7步:将顶点A加入到S中。 此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。 |
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ |
typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph;
typedef int Patharc[MAXVEX]; /* 数组元素为最短路径下标 */ typedef int ShortPathTable[MAXVEX];/* 数组元素为到各点的最短路径的权值和 */ |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j;
/* printf("请输入边数和顶点数:"); */ G->numEdges=16; G->numVertexes=9;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { G->vexs[i]=i; }
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } }
G->arc[0][1]=1; G->arc[0][2]=5; G->arc[1][2]=3; G->arc[1][3]=7; G->arc[1][4]=5;
G->arc[2][4]=1; G->arc[2][5]=7; G->arc[3][4]=2; G->arc[3][6]=3; G->arc[4][5]=3;
G->arc[4][6]=6; G->arc[4][7]=9; G->arc[5][7]=5; G->arc[6][7]=2; G->arc[6][8]=7;
G->arc[7][8]=4;
for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* Dijkstra算法,求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */ /* P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */ |
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D) { int v,w,k,min; int final[MAXVEX]; //当final[w]=1,说明已经求得了v0=vw的最短路径,我们不需要再考虑了 for(v=0; v<G.numVertexes; v++) /* 初始化数据 */ { final[v] = 0; /* 最开始全部顶点初始化为未知最短路径状态 */ (*D)[v] = G.arc[v0][v];/* 将与v0点有连线的顶点加上权值 */ (*P)[v] = 0; /* 初始化路径数组P为0 */ }
(*D)[v0] = 0; /* v0至v0路径为0 */ final[v0] = 1; /* v0至v0不需要求路径 */
/* 开始主循环,每次求得v0到某个v顶点的最短路径 */ for(v=1; v<G.numVertexes; v++) { min=INFINITY; /* 当前所知离v0顶点的最近距离 */ for(w=0; w<G.numVertexes; w++) //遍历数组D,寻找与v0最近的顶点,已经找到路径的顶点final=1就不需要再参与了 */ { if(!final[w] && (*D)[w]<min) { k=w; //找到后k存储这个最近点的下标 min = (*D)[w]; //找到后min存储这个最短路径的权值和 } } final[k] = 1; /* 将目前找到的最近的顶点置为1, 以后就不用再找 */ for(w=0; w<G.numVertexes; w++) /* 修正当前最短路径及距离 */ { /* 如果经过v顶点的路径比现在这条路径的长度短的话 */ if(!final[w] && (min+G.arc[k][w]<(*D)[w])) { /* 说明找到了更短的路径,修改D[w]和P[w] */ (*D)[w] = min + G.arc[k][w]; /* 修改当前路径长度 */ (*P)[w]=k; } } } } |
//主函数 |
int main(void) { int i,j,v0; MGraph G; Patharc P; ShortPathTable D; /* 求某点到其余各点的最短路径 */ v0=0;
CreateMGraph(&G);
ShortestPath_Dijkstra(G, v0, &P, &D);
printf("最短路径倒序如下:\n"); for(i=1;i<G.numVertexes;++i) { printf("v%d - v%d : ",v0,i); j=i; while(P[j]!=0) { printf("%d ",P[j]); j=P[j]; } printf("\n"); } printf("\n源点到各顶点的最短路径长度为:\n"); for(i=1;i<G.numVertexes;++i) printf("v%d - v%d : %d \n",G.vexs[0],G.vexs[i],D[i]); return 0; }
|
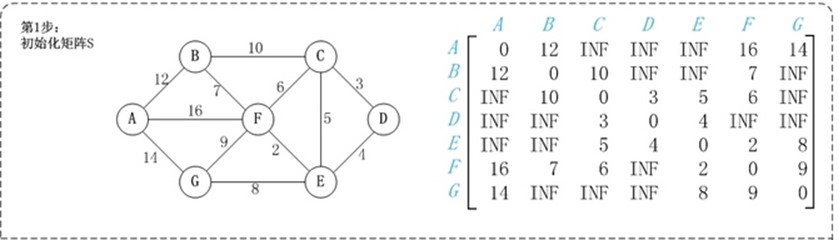
//版本1 |
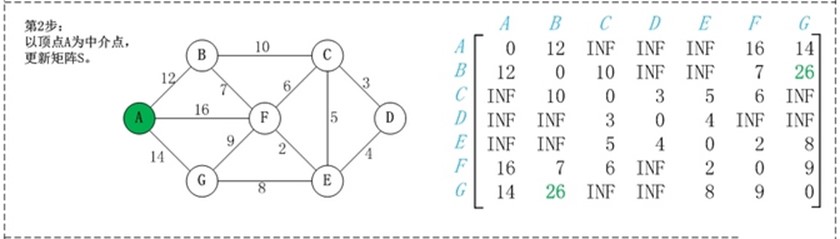
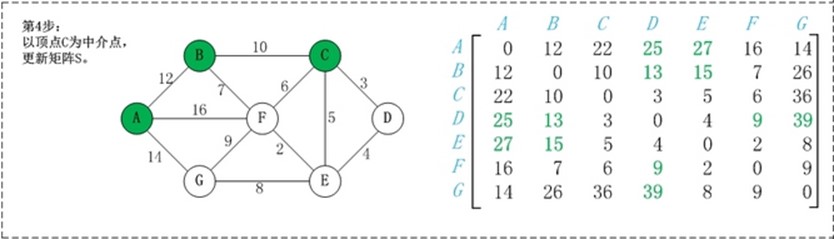
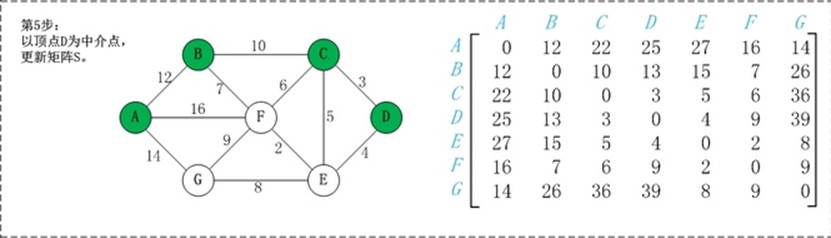
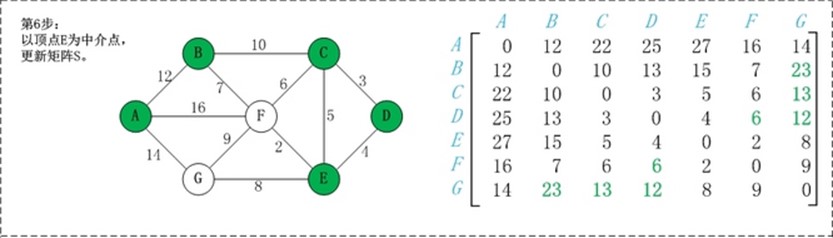
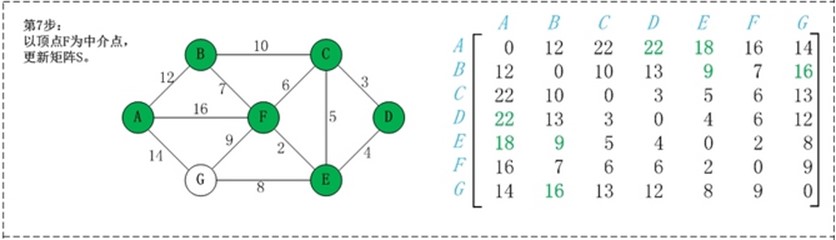
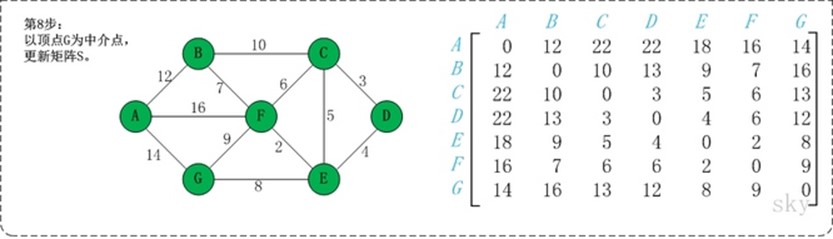
第1步:初始化矩阵S。 矩阵S中a[i][j]为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞。 第2步:以顶点A(第1个顶点)为中介点,若a[i][j] > a[i][0]+a[0][j],则设置a[i][j]=a[i][0]+a[0][j]。 在上面的图例中, a[1][6]即(B,G)=∞;而将A作为中介点时,a[i][0] 即(B,A)=12,a[0][j], 即(A,G)=14,a[i][j] > a[i][0]+a[0][j], 因此B和G之间的距离可以更新为26。 第3步: 依次将顶点B,C,D,E,F,G作为中介点,并更新a[i][j]的大小。 |
/* floyd最短路径: G -- 图 path -- 路径。path[i][j]=k表示,"顶点i"到"顶点j"的最短路径会经过顶点k。 dist -- 长度数组。即,dist[i][j]=sum表示,"顶点i"到"顶点j"的最短路径的长度是sum。 */ void floyd(Graph G, int path[][MAX], int dist[][MAX]) { int i,j,k; int tmp;
// 初始化 for (i = 0; i < G.vexnum; i++) { for (j = 0; j < G.vexnum; j++) { dist[i][j] = G.matrix[i][j]; // "顶点i"到"顶点j"的路径长度为"i到j的权值"。 path[i][j] = j; // "顶点i"到"顶点j"的最短路径经过了顶点j。 } }
// 计算最短路径 for (k = 0; k < G.vexnum; k++) { for (i = 0; i < G.vexnum; i++) { for (j = 0; j < G.vexnum; j++) { // 如果经过下标为k顶点路径比原两点间路径更短,则更新dist[i][j]和path[i][j] tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]); if (dist[i][j] > tmp) { // "i到j最短路径"对应的值设为更小的一个(即经过k) dist[i][j] = tmp; // "i到j最短路径"对应的路径,经过k path[i][j] = path[i][k]; } } } }
// 打印floyd最短路径的结果 printf("floyd: \n"); for (i = 0; i < G.vexnum; i++) { for (j = 0; j < G.vexnum; j++) printf("%2d ", dist[i][j]); printf("\n"); } } |
//版本2 |
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ |
typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph;
typedef int Patharc[MAXVEX][MAXVEX]; typedef int ShortPathTable[MAXVEX][MAXVEX]; |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j;
/* printf("请输入边数和顶点数:"); */ G->numEdges=16; G->numVertexes=9;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { G->vexs[i]=i; }
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } }
G->arc[0][1]=1; G->arc[0][2]=5; G->arc[1][2]=3; G->arc[1][3]=7; G->arc[1][4]=5;
G->arc[2][4]=1; G->arc[2][5]=7; G->arc[3][4]=2; G->arc[3][6]=3; G->arc[4][5]=3;
G->arc[4][6]=6; G->arc[4][7]=9; G->arc[5][7]=5; G->arc[6][7]=2; G->arc[6][8]=7;
G->arc[7][8]=4;
for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } }
} |
/* Floyd算法,求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]。 */ |
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D) { int v,w,k; for(v=0; v<G.numVertexes; ++v) /* 初始化D与P */ { for(w=0; w<G.numVertexes; ++w) { (*D)[v][w]=G.arc[v][w]; /* D[v][w]值即为对应点间的权值 */ (*P)[v][w]=w; /* 初始化P */ } } for(k=0; k<G.numVertexes; ++k) { for(v=0; v<G.numVertexes; ++v) { for(w=0; w<G.numVertexes; ++w) { if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w]) {/* 如果经过下标为k顶点路径比原两点间路径更短 */ (*D)[v][w]=(*D)[v][k]+(*D)[k][w];/* 将当前两点间权值设为更小的一个 */ (*P)[v][w]=(*P)[v][k];/* 路径设置为经过下标为k的顶点 */ } } } } } |
//主函数 |
int main(void) { int v,w,k; MGraph G;
Patharc P; ShortPathTable D; /* 求某点到其余各点的最短路径 */
CreateMGraph(&G);
ShortestPath_Floyd(G,&P,&D);
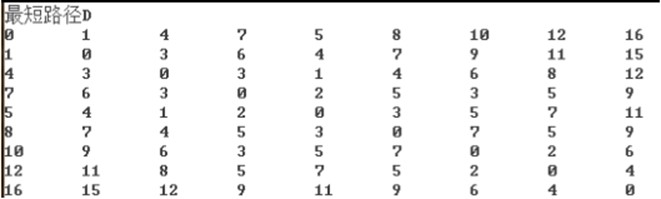
printf("各顶点间最短路径如下:\n"); for(v=0; v<G.numVertexes; ++v) { for(w=v+1; w<G.numVertexes; w++) { printf("v%d-v%d weight: %d ",v,w,D[v][w]); k=P[v][w]; /* 获得第一个路径顶点下标 */ printf(" path: %d",v); /* 打印源点 */ while(k!=w) /* 如果路径顶点下标不是终点 */ { printf(" -> %d",k); /* 打印路径顶点 */ k=P[k][w]; /* 获得下一个路径顶点下标 */ } printf(" -> %d\n",w); /* 打印终点 */ } printf("\n"); }
printf("最短路径D\n"); for(v=0; v<G.numVertexes; ++v) { for(w=0; w<G.numVertexes; ++w) { printf("%d\t",D[v][w]); } printf("\n"); } printf("最短路径P\n"); for(v=0; v<G.numVertexes; ++v) { for(w=0; w<G.numVertexes; ++w) { printf("%d ",P[v][w]); } printf("\n"); }
return 0; }
|
●
拓扑排序有两种常用的活动网络( Activity Network): ① AOV网(Activity On Vertices)——用顶点表示活动的网络; ② AOE网(Activity On Edges)——用边表示活动的网络
按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系。由此所得顶点的线性序列称之为拓扑有序序列。
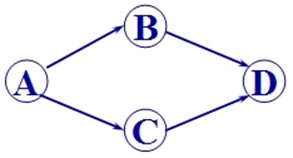
例如: 对于下列有向图:
可求得拓扑有序序列: A B C D 或 A C B D
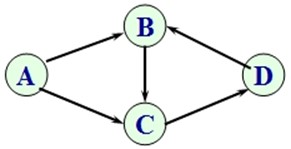
反之,对于下列有向图:
不能求得它的拓扑有序序列, 因为图中存在一个回路 {B, C, D} |
对AOV网进行拓扑排序的方法和步骤:
|
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXEDGE 20 #define MAXVEX 14 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ |
/* 邻接矩阵结构 */ |
typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; |
/* 邻接表结构 */ |
typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; |
/* 顶点表结点 */ |
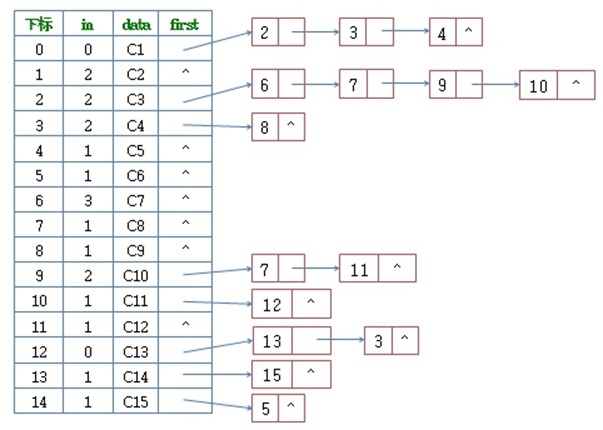
typedef struct VertexNode { int in; /* 顶点入度 */ int data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; |
typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j;
/* printf("请输入边数和顶点数:"); */ G->numEdges=MAXEDGE; G->numVertexes=MAXVEX;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { G->vexs[i]=i; }
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } }
G->arc[0][4]=1; G->arc[0][5]=1; G->arc[0][11]=1; G->arc[1][2]=1; G->arc[1][4]=1; G->arc[1][8]=1; G->arc[2][5]=1; G->arc[2][6]=1; G->arc[2][9]=1; G->arc[3][2]=1; G->arc[3][13]=1; G->arc[4][7]=1; G->arc[5][8]=1; G->arc[5][12]=1; G->arc[6][5]=1; G->arc[8][7]=1; G->arc[9][10]=1; G->arc[9][11]=1; G->arc[10][13]=1; G->arc[12][9]=1;
} |
/* 利用邻接矩阵构建邻接表 */ |
void CreateALGraph(MGraph G,GraphAdjList *GL) { int i,j; EdgeNode *e;
*GL = (GraphAdjList)malloc(sizeof(graphAdjList));
(*GL)->numVertexes=G.numVertexes; (*GL)->numEdges=G.numEdges; for(i= 0;i <G.numVertexes;i++) /* 读入顶点信息,建立顶点表 */ { (*GL)->adjList[i].in=0; (*GL)->adjList[i].data=G.vexs[i]; (*GL)->adjList[i].firstedge=NULL; /* 将边表置为空表 */ }
for(i=0;i<G.numVertexes;i++) /* 建立边表 */ { for(j=0;j<G.numVertexes;j++) { if (G.arc[i][j]==1) { e=(EdgeNode *)malloc(sizeof(EdgeNode)); e->adjvex=j; /* 邻接序号为j */ e->next=(*GL)->adjList[i].firstedge; /* 将当前顶点上的指向的结点指针赋值给e */ (*GL)->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */ (*GL)->adjList[j].in++;
} } }
} |
/* 拓扑排序,若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */ |
Status TopologicalSort(GraphAdjList GL) { EdgeNode *e; int i,k,gettop; int top=0; /* 用于栈指针下标 */ int count=0;/* 用于统计输出顶点的个数 */ int *stack; /* 建栈将入度为0的顶点入栈 */ stack=(int *)malloc(GL->numVertexes * sizeof(int) );
for(i = 0; i<GL->numVertexes; i++) if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */ stack[++top]=i; while(top!=0) { gettop=stack[top--]; printf("%d -> ",GL->adjList[gettop].data); count++; /* 输出i号顶点,并计数 */ for(e = GL->adjList[gettop].firstedge; e; e = e->next) { k=e->adjvex; if( !(--GL->adjList[k].in) ) /* 将i号顶点的邻接点的入度减1,如果减1后入度为0,则入栈, 以便下次循环输出 */ stack[++top]=k; } } printf("\n"); if(count < GL->numVertexes) //如果count小于顶点数, 说明存在环 return ERROR; else return OK; } |
//主函数 |
int main(void) { MGraph G; GraphAdjList GL; int result; CreateMGraph(&G); CreateALGraph(G,&GL); result=TopologicalSort(GL); printf("result:%d",result);
return 0; }
|
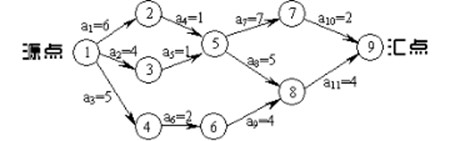
● 关键路径
路径长度: 路径上各个活动所持续的时间之和 关键路径: 从源点到汇点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动。
|
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXEDGE 30 #define MAXVEX 30 #define INFINITY 65535
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
int *etv,*ltv; /* 事件最早发生时间和最迟发生时间数组,全局变量 */ int *stack2; /* 用于存储拓扑序列的栈 */ int top2; /* 用于stack2的指针 */ |
/* 邻接矩阵结构 */ |
typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; |
/* 邻接表结构 */ |
typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; |
/* 顶点表结点 */ |
typedef struct VertexNode { int in; /* 顶点入度 */ int data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; |
typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; |
/* 构件图 */ |
void CreateMGraph(MGraph *G) { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=13; G->numVertexes=10;
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { G->vexs[i]=i; }
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j]=INFINITY; } }
G->arc[0][1]=3; G->arc[0][2]=4; G->arc[1][3]=5; G->arc[1][4]=6; G->arc[2][3]=8; G->arc[2][5]=7; G->arc[3][4]=3; G->arc[4][6]=9; G->arc[4][7]=4; G->arc[5][7]=6; G->arc[6][9]=2; G->arc[7][8]=5; G->arc[8][9]=3;
} |
/* 利用邻接矩阵构建邻接表 */ |
void CreateALGraph(MGraph G,GraphAdjList *GL) { int i,j; EdgeNode *e;
*GL = (GraphAdjList)malloc(sizeof(graphAdjList));
(*GL)->numVertexes=G.numVertexes; (*GL)->numEdges=G.numEdges; for(i= 0;i <G.numVertexes;i++) /* 读入顶点信息,建立顶点表 */ { (*GL)->adjList[i].in=0; (*GL)->adjList[i].data=G.vexs[i]; (*GL)->adjList[i].firstedge=NULL; /* 将边表置为空表 */ }
for(i=0;i<G.numVertexes;i++) /* 建立边表 */ { for(j=0;j<G.numVertexes;j++) { if (G.arc[i][j]!=0 && G.arc[i][j]<INFINITY) { e=(EdgeNode *)malloc(sizeof(EdgeNode)); e->adjvex=j; /* 邻接序号为j */ e->weight=G.arc[i][j]; e->next=(*GL)->adjList[i].firstedge; /* 将当前顶点上的指向的结点指针赋值给e */ (*GL)->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */ (*GL)->adjList[j].in++;
} } }
} |
/* 拓扑排序 */ |
Status TopologicalSort(GraphAdjList GL) { /* 若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */ EdgeNode *e; int i,k,gettop; int top=0; /* 用于栈指针下标 */ int count=0;/* 用于统计输出顶点的个数 */ int *stack; /* 建栈将入度为0的顶点入栈 */ stack=(int *)malloc(GL->numVertexes * sizeof(int) ); for(i = 0; i<GL->numVertexes; i++) if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */ stack[++top]=i;
top2=0; etv=(int *)malloc(GL->numVertexes * sizeof(int) ); /* 事件最早发生时间数组 */ for(i=0; i<GL->numVertexes; i++) etv[i]=0; /* 初始化 */ stack2=(int *)malloc(GL->numVertexes * sizeof(int) );/* 初始化拓扑序列栈 */
printf("TopologicalSort:\t"); while(top!=0) { gettop=stack[top--]; printf("%d -> ",GL->adjList[gettop].data); count++; /* 输出i号顶点,并计数 */
stack2[++top2]=gettop; /* 将弹出的顶点序号压入拓扑序列的栈 */
for(e = GL->adjList[gettop].firstedge; e; e = e->next) { k=e->adjvex; if( !(--GL->adjList[k].in) ) /* 将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 */ stack[++top]=k;
if((etv[gettop] + e->weight)>etv[k]) /* 求各顶点事件的最早发生时间etv值 */ etv[k] = etv[gettop] + e->weight; } } printf("\n"); if(count < GL->numVertexes) return ERROR; else return OK; } |
/* 求关键路径,GL为有向网,输出G的各项关键活动 */ |
void CriticalPath(GraphAdjList GL) { EdgeNode *e; int i,gettop,k,j; int ete,lte; /* 声明活动最早发生时间和最迟发生时间变量 */ TopologicalSort(GL); /* 求拓扑序列,计算数组etv和stack2的值 */ ltv=(int *)malloc(GL->numVertexes*sizeof(int));/* 事件最早发生时间数组 */ for(i=0; i<GL->numVertexes; i++) ltv[i]=etv[GL->numVertexes-1]; /* 初始化 */
printf("etv:\t"); for(i=0; i<GL->numVertexes; i++) printf("%d -> ",etv[i]); printf("\n");
while(top2!=0) /* 出栈是求ltv */ { gettop=stack2[top2--]; for(e = GL->adjList[gettop].firstedge; e; e = e->next) /* 求各顶点事件的最迟发生时间ltv值 */ { k=e->adjvex; if(ltv[k] - e->weight < ltv[gettop]) ltv[gettop] = ltv[k] - e->weight; } }
printf("ltv:\t"); for(i=0; i<GL->numVertexes; i++) printf("%d -> ",ltv[i]); printf("\n");
for(j=0; j<GL->numVertexes; j++) /* 求ete,lte和关键活动 */ { for(e = GL->adjList[j].firstedge; e; e = e->next) { k=e->adjvex; ete = etv[j]; /* 活动最早发生时间 */ lte = ltv[k] - e->weight; /* 活动最迟发生时间 */ if(ete == lte) /* 两者相等即在关键路径上 */ printf("<v%d - v%d> length: %d \n",GL->adjList[j].data,GL->adjList[k].data,e->weight); } } } |
//主函数 |
int main(void) { MGraph G; GraphAdjList GL; CreateMGraph(&G); CreateALGraph(G,&GL); CriticalPath(GL); return 0; }
|


























 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号