组合数学笔记

组合恒等式

　　$\binom{n}{m}=\binom{n}{n-m}$

　　$\sum_{i=0}^n\binom{n}{i}=2^n$

　　$\sum_{i=0}^n\binom{n}{i}[2|i]=\sum_{i=0}^n\binom{n}{i}![2|i]=2^{n-1}$

　　$k$个非负整数变量和为$n$的方案数（插板法）$\binom{n+k-1}{k-1}$

　　$\sum_{i=0}^m\binom{n+i}{n}=\binom{n+m+1}{m}$

　　$\sum_{i=m}^n\binom{i}{m}=\binom{n+1}{m+1}$

　　$\binom{n}{m}\binom{m}{k}=\binom{n}{k}\binom{n-k}{m-k}$

　　$\sum_{i=0}^k\binom{n}{i}\binom{m}{k-i}=\binom{n+m}{k}$

　　$S_k(n)=\sum_{i=1}^n$ $S_k(n)$是关于$n$的$k+1$次多项式

　　拉格朗日插值：对于$k$次多项式函数$F$以及$k+1$个点值$(x_0,y_0),(x_1,y_1),\cdots ,(x_k,y_k)$,有$F(x)=\sum_{i=0}^ky_i\prod _{i\neq j}\frac{x-x_j}{x_i-x_j}$

　　斯特林数：$S_k(n)=\frac{(n+1)^{\underline{k+1}}}{k+1}-\sum_{i=0}^{k-1}(-1)^{k-i}\cdot \begin{bmatrix}k\\i\end{bmatrix}\cdot S_i(n)$

　　伯努利数：$\frac{x}{e^x-1}=\sum_{i=0}^{\infty }\frac{B_i}{i!}x^i$

　　伯努利多项式：$\sum_{i=0}^{\infty}\frac{\beta _i(t)}{i!}\cdot x^i=\frac{x}{e^x-1}\cdot e^{tx}$

　　$S_k(n)=\frac{1}{k+1}\sum_{i=0}^k\binom{k+1}{i}\cdot (n+1)^i\cdot B_{k+1-i}$，令$n=0$，则$\sum_{i=0}^k\binom{k+1}{i}B_i=0$

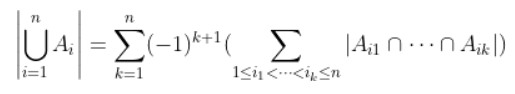　　不知道为啥显示不出来，就用图片了

　　$\left | \bigcap_{i=1}^{n}A_i \right |=\sum_{S\subseteq [n]}(-1)^{|S|}\left | \bigcap_{i\in S}\bar{A_i} \right |$

　　$max\left \{ S \right \}=\sum_{T\subseteq S}(-1)^{|T|+1}min\left \{ T \right \}$

　　属于卡特兰数列的问题：

　　.有$2n$个人排成一行进入剧场。入场费$5$元，其中有$n$个人有一张$5$元钞票，$n$个人有一张$10$元钞票，剧场中无其他钞票，问有多少种方法使得每一个有$10$元的人买票，售票处就有$5$元找零

　　.从$(0,0)$走到$(n,n)$，每次只能向右或向上移动一格，且路线不能穿过对角线（但可以碰到对角线），问有多少种方法

　　.在圆上选择$2n$个点，将这些点连成$n$条线段并且线段之间没有交点，有多少种方法

　　.对角线不相交的情况下，将一个凸多边形分成三角形的方案数

　　.一个栈（无穷大）的进栈顺序为$1,2,3,\cdots ,n$，问有多少种出栈顺序

　　.$n$个结点可以构造成多少个不同的二叉树

　　.$n$个$+1$和$n$个$-1$构成$2n$项$a_1,a_2,\cdots,a_{2n}$，其部分满足$a_1+a_2+\cdots+a_k \geq 0 (k=1,2,3,\cdots ,2n)$对于$n$该数列为？

posted on 2021-08-23 09:15 ArrogHie 阅读(147) 评论(0) 编辑收藏举报