计算几何超详细板子
定义
点与向量
struct Point { double x, y; Point() {} Point(double x, double y) :x(x), y(y) {} }; typedef Point Vector;
线段与直线
struct Segment { Point a, b; Segment() {} Segment(Point a, Point b) :a(a), b(b) {} }; typedef Segment Line;
圆
struct Circle { Point c; double r; Circle() {} Circle(Point c, double r) :c(c), r(r) {} };
多边形
typedef vector<Point> polygon;
向量的基本运算
Point operator + (Point& b) { return Point(x + b.x, y + b.y); } Point operator - (Point& b) { return Point(x - b.x, y - b.y); } Point operator * (double k) { return Point(x * k, y * k); }
向量的运算
向量的模长(向量的长度)
范数则为向量长度的平方
double norm(Vector a)//范数 { return pow(a.x, 2) + pow(a.y, 2); } double abs(Vector a)//模长 { return sqrt(norm(a)); }
向量的内积$a · b = |a||b|cos\theta $
内积为负则夹角为钝角
double dot(Vector a, Vector b)//|a||b|cos A { return a.x * b.x + a.y * b.y; }
向量的外积$a \times b = |a||b|sin\theta $
double cross(Vector a, Vector b)//|a||b|sin A { return a.x * b.y - a.y * b.x; }
直线的正交/平行判定
当$a$与$b$的内积为$0$时两向量正交(垂直)
bool isOrthogonal(Vector a, Vector b) { return equals(dot(a, b), 0.0); } bool isOrthogonal(Point a1, Point a2, Point b1, Point b2) { return isOrthogonal(a1 - a2, b1 - b2); } bool isOrthogonal(Segment s1, Segment s2) { return isOrthogonal(Vector(s1.a - s1.b), Vector(s2.a - s2.b)); }
当$a$与$b$外积为$0$时两向量平行
bool isParallel(Vector a, Vector b) { return equals(cross(a, b), 0.0); } bool isParallel(Point a1, Point a2, Point b1, Point b2) { return isParallel(a1 - a2, b1 - b2); } bool isParallel(Segment s1, Segment s2) { return isParallel(Vector(s1.a - s1.b), Vector(s2.a - s2.b)); }
投影
求点$P$在直线$s$上的投影
Point project(Point p, Segment s) { Vector base = s.p2 - s.p1; double r = dot(p - s.p1, base) / norm(base); base = base * r; return Point(s.p1 + base); }
映射
求点$P$对于直线$s$的映像(对称点)
Point reflect(Point p, Segment s) { Point p1 = (project(p, s) - p) * 2.0; return p + p1; }
距离
两点之间距离
double get_dis(Point a, Point b) { return abs(a - b); }
点与直线距离
通过外积求出点与直线上两点形成的平行四边形的面积,此时点到直线的距离就是平行四边形的面积的高,再用面积除以底边即可
double get_dis(Point a, Line l) { return abs(cross(l.p2 - l.p1, a - l.p1) / abs(l.p2 - l.p1)); }
点与线段距离
分三种情况讨论:
·点作垂直与线段的垂线在线段内,直接当点与直线的距离算
·否则算点到两个端点的距离,其中小的一个就是点到线段的距离
double get_dis_ps(Point p, Segment s) { if (dot(p - s.p1, s.p2 - s.p1) < 0.0) return abs(p - s.p1); if (dot(p - s.p2, s.p1 - s.p2) < 0.0) return abs(p - s.p2); return get_dis(p, s); }
线段与线段的距离
为其中一个线段的端点到另一个线段的距离的最小值
double get_dis(Segment a, Segment b) { if (intersect(a, b)) return 0.0;//判断两直线相交 后面说 return min(min(get_dis_ps(a.p1, b), get_dis_ps(a.p2, b)), min(get_dis_ps(b.p1, a), get_dis_ps(b.p2, a))); }
位置
顺逆时针方向
对于两向量$a,b$的外积,若外积为正则$b$在$a$的逆时针方向,为负则为顺时针方向,为$0$则在同一直线,此时若内积为负则两向量方向相反,否则相同
//b在a的 const int CC = 1;//逆时针方向 const int C = -1;//顺时针方向 const int OB = 2;//方向相反 const int OF = -2;//方向相同 |b|>|a| const int OS = 0;//方向相同 |a|>|b| inline int ccw(Point p1, Point p2, Point p3) { Vector a = p2 - p1; Vector b = p3 - p1; if (cross(a, b) > eps) return CC; if (cross(a, b) < -eps) return C; if (dot(a, b) < -eps) return OB; if (norm(a) < norm(b)) return OF; return OS; } inline int ccw(Vector a, Vector b) { if (cross(a, b) > eps) return CC; if (cross(a, b) < -eps) return C; if (dot(a, b) < -eps) return OB; if (norm(a) < norm(b)) return OF; return OS; }
判断线段相交
若一条线段的两个端点都在另一条线段的两边(顺逆时针方向都有),则它们相交
inline bool intersect(Point a, Point b, Point c, Point d) { return ccw(a, b, c) * ccw(a, b, d) <= 0 && ccw(c, d, a) * ccw(c, d, b) <= 0; } inline bool intersect(Segment a, Segment b) { return intersect(a.p1, a.p2, b.p1, b.p2); }
求交点
线段的交点
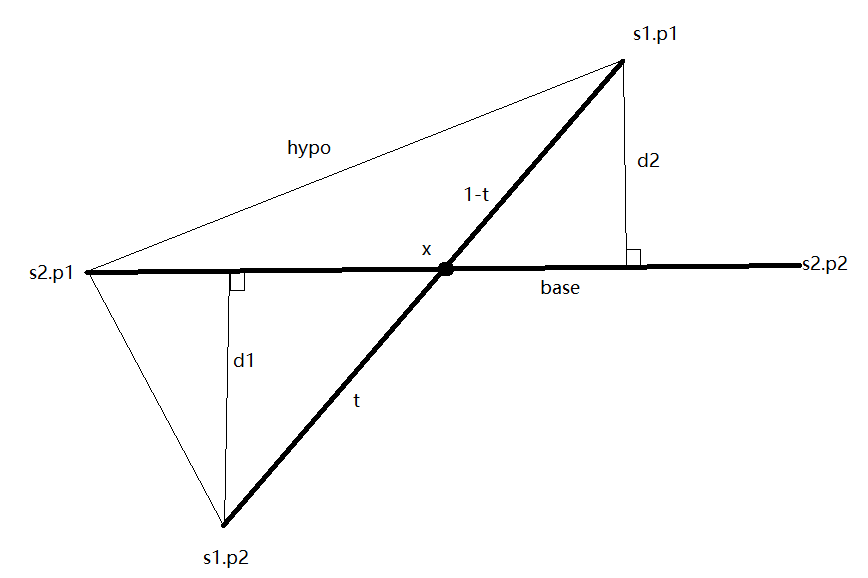
$base=s2.p2-s2.p1 , typo=s1.p1-s2.p1$
$d1=\frac{cross(typo,base)}{|base|}$
$d2=\frac{cross(s1.p2-s2.p1,base)}{|base|}$
$d1:d2=t:(1-t)$
$t=\frac{d1}{d1+d2}$
$x=s1.p1+(s1.p2-s1.p1)\times t$
Point getCrossPoint(Segment s1, Segment s2) { Vector base = s2.p2 - s2.p1; double d1 = abs(cross(base, s1.p1 - s2.p1)); double d2 = abs(cross(base, s1.p2 - s2.p1)); double t = d1 / (d1 + d2); Point x = (s1.p2 - s1.p1) * t; return s1.p1 + x; }
圆与直线的交点
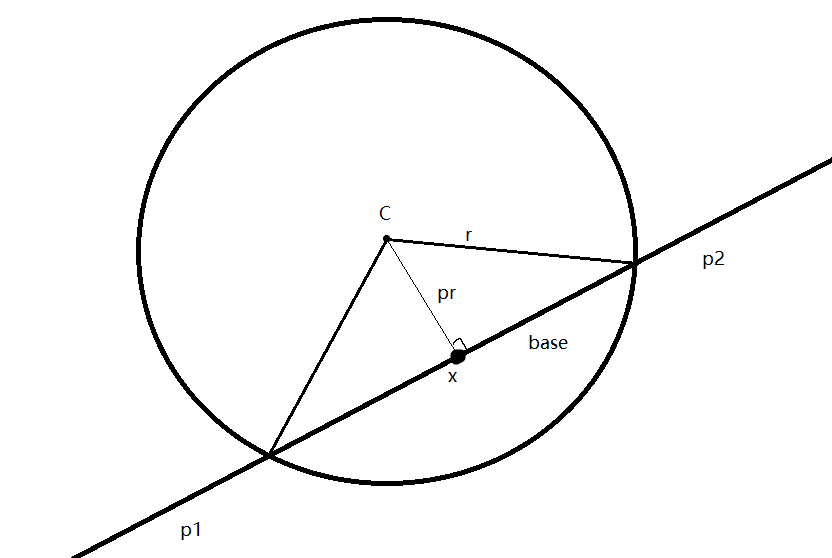
直线上的单位向量为$e$
$e=e=\frac{p2-p1}{|p2-p1|}$
$x=project(c,(p2,p1))$
$pr=x-c$
$base=\sqrt{r^{2}-|pr-c|^{2}}$
交点即为$x\pm base*e$
pair<Point, Point> getCrossPoint(Line l, Circle C) { if (get_dis(C.c, l) > C.r) return make_pair(Point(2e18, 2e18), Point(2e18, 2e18)); Point pr = project(C.c, l); Vector e = (l.p2 - l.p1) / abs(l.p2 - l.p1); double base = sqrt(C.r * C.r - norm(pr - C.c)); Vector x = e * base; return make_pair(pr + x, pr - x); }
凸包
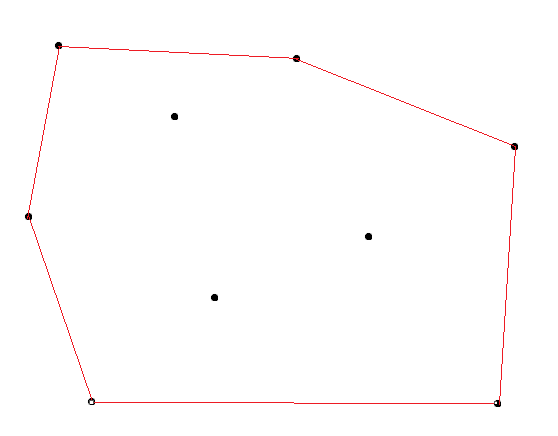
包含点集$p$的面积最小的凸多边形成为$p$的凸包(如下图,红色部分即为凸包)
安德鲁算法:
将点的x作为第一关键字,y作为第二关键字进行排序,之后遍历一遍,将遍历的点依次加入栈中当做凸多边形的边上的点,加入的方法如下:
当加入当前点后(该点未入栈),若凸多边形不满足多边形性质,则将栈顶的点弹出,不断重复这一操作直到加入当前点后凸包满足凸多边形性质(即不会出现凹下去的地方),此时再将当前点入栈。
这样能完成凸包的上半部分,之后再逆序遍历一边,依然按上述方法加点,将所有点遍历完毕则栈内的所有点形成的点集便是凸包的顶点。
inline Polygon andrewScan(Polygon p)//返回凸包的点集 { Polygon u, d; if (p.size() < 3) return p; sort(p.begin(), p.end()); u.pb(p[0]); u.pb(p[1]); d.pb(p[p.size() - 1]); d.pb(p[p.size() - 2]); for (int i = 2; i < p.size(); i++) { for (int k = u.size(); k >= 2 && ccw(u[k - 2], u[k - 1], p[i]) != C; k--) u.pop_back(); u.pb(p[i]); } for (int i = p.size() - 3; ~i; i--) { for (int k = d.size(); k >= 2 && ccw(d[k - 2], d[k - 1], p[i]) != C; k--) d.pop_back(); d.pb(p[i]); } reverse(d.begin(), d.end()); for (int i = u.size() - 2; i; i--) d.pb(u[i]); return d; }
扫描线
一种算法,就是一条线在图上从左到右(从哪到哪都行)扫一遍,一般解决图形的面积和周长问题
例题:

#include<cstdio> #include<cstring> #include<vector> #include<map> #include<iostream> #include<algorithm> using namespace std; #define pb push_back typedef long long LL; const int N = 1010; int n, m; vector<int> hash1; map<int, int> st; struct Tree { int len, d; Tree() {} Tree(int len, int d) :len(len), d(d) {} }tr[N << 4]; struct Node { int y, l, r, d; Node() {} Node(int y, int l, int r, int d) :y(y), l(l), r(r), d(d) {} }; vector<Node> a; inline bool cmp(Node a, Node b) { return a.y < b.y; } inline void pushup(int q, int l, int r) { if (tr[q].d > 0) tr[q].len = hash1[r] - hash1[l - 1]; else if (l == r) tr[q].len = 0; else tr[q].len = tr[q << 1].len + tr[q << 1 | 1].len; } void modify(int q, int l, int r, int L, int R, int x) { if (L <= l && r <= R) { tr[q].d += x; pushup(q, l, r); return; } int mid = l + r >> 1; if (L <= mid) modify(q << 1, l, mid, L, R, x); if (R > mid) modify(q << 1 | 1, mid + 1, r, L, R, x); pushup(q, l, r); } inline LL solve() { LL ans = 0; for (int i = 0; i < a.size(); i++) { if (i != 0) ans += 1ll * tr[1].len * (a[i].y - a[i - 1].y); modify(1, 1, m, st[a[i].l], st[a[i].r] - 1, a[i].d); } return ans; } int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) { int x1, y1, x2, y2; scanf("%d%d%d%d", &x1, &y1, &x2, &y2); hash1.pb(x1), hash1.pb(x2); a.pb(Node(y1, x1, x2, 1)); a.pb(Node(y2, x1, x2, -1)); } sort(hash1.begin(), hash1.end()); hash1.erase(unique(hash1.begin(), hash1.end()), hash1.end()); m = hash1.size(); for (int i = 0; i < m; i++) st[hash1[i]] = i + 1; sort(a.begin(), a.end(), cmp); printf("%lld", solve()); }

#include<cstdio> #include<cstring> #include<vector> #include<cmath> #include<iostream> #include<algorithm> using namespace std; #define x first #define y second typedef pair<double, double> PDD; const int N = 110; const double eps = 1e-8, INF = 1e6; int n; PDD tr[N][3]; PDD q[N]; int sign(double x) { if (fabs(x) < eps) return 0; if (x < 0) return -1; return 1; } int dcmp(double x, double y) { if (fabs(x - y) < eps) return 0; if (x < y) return -1; return 1; } PDD operator+ (PDD a, PDD b) { return { a.x + b.x, a.y + b.y }; } PDD operator- (PDD a, PDD b) { return { a.x - b.x, a.y - b.y }; } PDD operator* (PDD a, double t) { return { a.x * t, a.y * t }; } double operator* (PDD a, PDD b) { return a.x * b.y - a.y * b.x; } double operator& (PDD a, PDD b) { return a.x * b.x + a.y * b.y; } bool on_segment(PDD p, PDD a, PDD b) { return sign((p - a) & (p - b)) <= 0; } PDD getCrossPoint(PDD p, PDD v, PDD q, PDD w) { if (!sign(v * w)) return { INF, INF }; auto u = p - q; auto t = w * u / (v * w); auto o = p + v * t; if (!on_segment(o, p, p + v) || !on_segment(o, q, q + w)) return { INF, INF }; return o; } double line_area(double a, int side) { int cnt = 0; for (int i = 0; i < n; i++) { auto t = tr[i]; if (dcmp(t[0].x, a) > 0 || dcmp(t[2].x, a) < 0) continue; if (!dcmp(t[0].x, a) && !dcmp(t[1].x, a)) { if (side) q[cnt++] = { t[0].y, t[1].y }; } else if (!dcmp(t[2].x, a) && !dcmp(t[1].x, a)) { if (!side) q[cnt++] = { t[2].y, t[1].y }; } else { double d[3]; int u = 0; for (int j = 0; j < 3; j++) { auto o = getCrossPoint(t[j], t[(j + 1) % 3] - t[j], { a, -INF }, { 0, INF * 2 }); if (dcmp(o.x, INF)) d[u++] = o.y; } if (u) { sort(d, d + u); q[cnt++] = { d[0], d[u - 1] }; } } } if (!cnt) return 0; for (int i = 0; i < cnt; i++) { if (q[i].x > q[i].y) swap(q[i].x, q[i].y); } sort(q, q + cnt); double res = 0, st = q[0].x, ed = q[0].y; for (int i = 1; i < cnt; i++) { if (q[i].x <= ed) ed = max(ed, q[i].y); else { res += ed - st; st = q[i].x, ed = q[i].y; } } res += ed - st; return res; } double range_area(double a, double b) { return (line_area(a, 1) + line_area(b, 0)) * (b - a) / 2; } int main() { scanf("%d", &n); vector<double> xs; for (int i = 0; i < n; i++) { for (int j = 0; j < 3; j++) { scanf("%lf%lf", &tr[i][j].x, &tr[i][j].y); xs.push_back(tr[i][j].x); } sort(tr[i], tr[i] + 3); } for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { for (int x = 0; x < 3; x++) { for (int y = 0; y < 3; y++) { auto o = getCrossPoint(tr[i][x], tr[i][(x + 1) % 3] - tr[i][x], tr[j][y], tr[j][(y + 1) % 3] - tr[j][y]); if (dcmp(o.x, INF)) xs.push_back(o.x); } } } } sort(xs.begin(), xs.end()); double res = 0; for (int i = 0; i + 1 < xs.size(); i++) { if (dcmp(xs[i], xs[i + 1])) res += range_area(xs[i], xs[i + 1]); } printf("%.2lf\n", res); }
求多边形面积(Shoelace Theorem,鞋带定理)
设$n$边形的顶点点集为$\begin{Bmatrix}(x_0,y_0),(x_1,y_1),(x_2,y_2),...(x_{n-1},y_{n-1})\end{Bmatrix}$
则多边形的面积为
$S=\frac{1}{2}\sum_{i=0}^{n-1}(cross((x_i,y_i),(x_{i+1\textit{ mod n}},y_{i+1\textit{ mod n}})))=\frac{1}{2}\sum_{i=0}^{n-1}(x_iy_{i+1\textit{ mod n}}-y_ix_{i+1\textit{ mod n}})$
证明见传送门
inline double Ploygon_area(Polygon s) { int n = s.size(); double ans = 0.0; for (int i = 0; i < n; i++) { ans += cross(s[i], s[(i + 1) % n]); } return ans * 0.5; }
半平面交
概念见OI_Wiki

inline double get_atan2(Point a, Point b) { Vector v = b - a; return atan2(v.y, v.x); } struct Segment//重新定义直线,加了一个极角 { Point p1, p2;//起点为p1 double ang; Segment() {} Segment(Point a, Point b) :p1(a), p2(b), ang(get_atan2(p1, p2)) {} }; inline bool cmp_ang(Segment a, Segment b)//按极角排序 { return a.ang < b.ang; } inline bool OnLeft(Point p, Line s)//判断点是否在直线的左边 { return cross(s.p2 - s.p1, p - s.p1) > 0.0; } inline Polygon HPI(vector<Segment> L) { int n = L.size(); sort(L.begin(), L.end(), cmp_ang); int head, tail; vector<Point> p(n);//交点点集 vector<Segment> q(n);//保留的直线 vector<Point> ans; q[head = tail = 0] = L[0]; for (int i = 1; i < n; i++) { while (head < tail && !OnLeft(p[tail - 1], L[i])) tail--; while (head < tail && !OnLeft(p[head], L[i])) head++; q[++tail] = L[i]; if (equals(cross(q[tail].p2 - q[tail].p1, q[tail - 1].p2 - q[tail - 1].p1), 0.0)) { tail--; if (OnLeft(L[i].p1, q[tail])) q[tail] = L[i]; } if (head < tail) p[tail - 1] = getCrossPoint(q[tail - 1], q[tail], 1); } while (head < tail && !OnLeft(p[tail - 1], q[head])) tail--; if (head == tail) return ans; p[tail] = getCrossPoint(q[tail], q[head], 1); for (int i = head; i <= tail; i++) ans.pb(p[i]); return ans;//返回交点的点集 }
旋转卡壳
一种算法,由两条或多条平行线去卡一个凸多边形,一般求关于凸多边形的直径或距离最大的点对
如下图,两条平行线(红色)卡住一个凸包

例题:

#include<cstdio> #include<cstring> #include<cmath> #include<iostream> #include<algorithm> using namespace std; const int N = 50010; const double eps = 1e-8; int n; int stk[N], top; bool st[N]; struct Point { double x, y; Point() {} Point(double x, double y) :x(x), y(y) {} }a[N]; typedef Point Vector; inline bool equal(double a, double b) { return fabs(a - b) <= eps; } inline bool cmp(Point a, Point b) { return equal(a.x, b.x) ? a.y < b.y : a.x < b.x; } inline Vector sub(Point a, Point b) { return Vector(a.x - b.x, a.y - b.y); } inline double cross(Vector a, Vector b) { return a.x * b.y - a.y * b.x; } inline double area(Point a, Point b, Point c) { return cross(sub(b, a), sub(c, a)); } inline void get_convex() { sort(a + 1, a + 1 + n, cmp); for (int i = 1; i <= n; i++) { while (top >= 2 && area(a[stk[top - 1]], a[stk[top]], a[i]) <= 0) { if (area(a[stk[top - 1]], a[stk[top]], a[i]) < 0) st[stk[top--]] = false; else top--; } stk[++top] = i; st[i] = true; } st[1] = false; for (int i = n; i; i--) { if (st[i]) continue; while (top >= 2 && area(a[stk[top - 1]], a[stk[top]], a[i]) <= 0) top--; stk[++top] = i; } top--; } inline double get_dis(Point a, Point b) { return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)); } inline double rotating_calipers() { if (top <= 2) return pow(get_dis(a[1], a[n]), 2); double res = 0; for (int i = 1, j = 3; i <= top; i++) { Point d = a[stk[i]], e = a[stk[i + 1]]; while (area(d, e, a[stk[j]]) < area(d, e, a[stk[j + 1]])) { if (j + 1 > top) j = 1; else j++; } res = max(res, max(get_dis(d, a[stk[j]]), get_dis(e, a[stk[j]]))); } return pow(res, 2); } int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%lf%lf", &a[i].x, &a[i].y); get_convex(); printf("%.0lf", rotating_calipers()); }

#include<cstdio> #include<cstring> #include<cmath> #include<vector> #include<iostream> #include<algorithm> using namespace std; #define x first #define y second using namespace std; typedef pair<double, double> PDD; const int N = 50010; const double eps = 1e-12, INF = 1e20; const double PI = acos(-1); int n; int stk[N], top; PDD q[N]; PDD ans[N]; double min_area = INF; bool st[N]; int sign(double x) { if (fabs(x) < eps) return 0; if (x < 0) return -1; return 1; } int dcmp(double x, double y) { if (fabs(x - y) < eps) return 0; if (x < y) return -1; return 1; } PDD operator+ (PDD a, PDD b) { return { a.x + b.x, a.y + b.y }; } PDD operator- (PDD a, PDD b) { return { a.x - b.x, a.y - b.y }; } PDD operator* (PDD a, double t) { return { a.x * t, a.y * t }; } PDD operator/ (PDD a, double t) { return { a.x / t, a.y / t }; } double operator* (PDD a, PDD b) { return a.x * b.y - a.y * b.x; } double operator& (PDD a, PDD b) { return a.x * b.x + a.y * b.y; } double area(PDD a, PDD b, PDD c) { return (b - a) * (c - a); } double get_len(PDD a) { return sqrt(a & a); } double project(PDD a, PDD b, PDD c) { return ((b - a) & (c - a)) / get_len(b - a); } PDD norm(PDD a) { return a / get_len(a); } PDD rotate(PDD a, double b) { return { a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b) }; } void get_convex() { sort(q, q + n); for (int i = 0; i < n; i++) { while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0) st[stk[--top]] = false; stk[top++] = i; st[i] = true; } st[0] = false; for (int i = n - 1; i >= 0; i--) { if (st[i]) continue; while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0) top--; stk[top++] = i; } reverse(stk, stk + top); top--; } void rotating_calipers() { for (int i = 0, a = 2, b = 2, c = 2; i < top; i++) { auto d = q[stk[i]], e = q[stk[i + 1]]; while (dcmp(area(d, e, q[stk[a]]), area(d, e, q[stk[a + 1]])) < 0) a = (a + 1) % top; while (dcmp(project(d, e, q[stk[b]]), project(d, e, q[stk[b + 1]])) < 0) b = (b + 1) % top; if (!i) c = a; while (dcmp(project(d, e, q[stk[c]]), project(d, e, q[stk[c + 1]])) > 0) c = (c + 1) % top; auto x = q[stk[a]], y = q[stk[b]], z = q[stk[c]]; auto h = area(d, e, x) / get_len(e - d); auto w = ((y - z) & (e - d)) / get_len(e - d); if (h * w < min_area) { min_area = h * w; ans[0] = d + norm(e - d) * project(d, e, y); ans[3] = d + norm(e - d) * project(d, e, z); auto u = norm(rotate(e - d, -PI / 2)); ans[1] = ans[0] + u * h; ans[2] = ans[3] + u * h; } } } int main() { scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%lf%lf", &q[i].x, &q[i].y); get_convex(); rotating_calipers(); int k = 0; for (int i = 1; i < 4; i++) { if (dcmp(ans[i].y, ans[k].y) < 0 || !dcmp(ans[i].y, ans[k].y) && dcmp(ans[i].x, ans[k].x)) { k = i; } } printf("%.5lf\n", min_area); for (int i = 0; i < 4; i++, k++) { auto x = ans[k % 4].x, y = ans[k % 4].y; if (!sign(x)) x = 0; if (!sign(y)) y = 0; printf("%.5lf %.5lf\n", x, y); } return 0; }
整合包

#include<cstdio> #include<cstring> #include<cmath> #include<vector> #include<map> #include<iostream> #include<algorithm> using namespace std; #define pb push_back const int N = 500010; const double eps = 1e-8; inline bool equals(double a, double b)//判断相等 { return fabs(a - b) < eps; } struct Point//点 向量 { double x, y; Point() {} Point(double x, double y) :x(x), y(y) {} Point operator + (Point& b) { return Point(x + b.x, y + b.y); } Point operator - (Point& b) { return Point(x - b.x, y - b.y); } Point operator * (double k) { return Point(x * k, y * k); } Point operator / (double k) { return Point(x / k, y / k); } bool operator < (Point b) { return equals(x, b.x) ? y < b.y : x < b.x; } }; typedef Point Vector; inline double get_atan2(Point a, Point b)//求极角 { Vector v = b - a; return atan2(v.y, v.x); } struct Segment//线段 直线 射线 { Point p1, p2;//若表示射线则起点为p1 double ang; Segment() {} Segment(Point a, Point b) :p1(a), p2(b), ang(get_atan2(p1, p2)) {} }; typedef Segment Line; struct Circle//圆 { Point c; double r; Circle() {} Circle(Point c, double r) :c(c), r(r) {} }; typedef vector<Point> Polygon;//多边形 double norm(Vector a)//范数 { return pow(a.x, 2) + pow(a.y, 2); } double abs(Vector a)//模长 { return sqrt(norm(a)); } double dot(Vector a, Vector b)//|a||b|cos A { return a.x * b.x + a.y * b.y; } inline double cross(Vector a, Vector b)//|a||b|sin A { return a.x * b.y - a.y * b.x; } bool isOrthogonal(Vector a, Vector b)//判断正交 { return equals(dot(a, b), 0.0); } bool isOrthogonal(Point a1, Point a2, Point b1, Point b2) { return isOrthogonal(a1 - a2, b1 - b2); } bool isOrthogonal(Segment s1, Segment s2) { return isOrthogonal(Vector(s1.p1 - s1.p2), Vector(s2.p1 - s2.p2)); } bool isParallel(Vector a, Vector b)//判断平行 { return equals(cross(a, b), 0.0); } bool isParallel(Point a1, Point a2, Point b1, Point b2) { return isParallel(a1 - a2, b1 - b2); } bool isParallel(Segment s1, Segment s2) { return isParallel(Vector(s1.p1 - s1.p2), Vector(s2.p1 - s2.p2)); } Point project(Point p, Segment s)//求投影 { Vector base = s.p2 - s.p1; double r = dot(p - s.p1, base) / norm(base); base = base * r; return Point(s.p1 + base); } Point reflect(Point p, Segment s)//求映射 { Point p1 = (project(p, s) - p) * 2.0; return p + p1; } double get_dis(Point a, Point b)//求点之间距离 { return abs(a - b); } double get_dis(Point a, Line l)//求点与直线之间距离 { return abs(cross(l.p2 - l.p1, a - l.p1) / abs(l.p2 - l.p1)); } double get_dis_ps(Point p, Segment s)//求点与线段距离 { if (dot(p - s.p1, s.p2 - s.p1) < 0.0) return abs(p - s.p1); if (dot(p - s.p2, s.p1 - s.p2) < 0.0) return abs(p - s.p2); return get_dis(p, s); } inline bool intersect(Point, Point, Point, Point); inline bool intersect(Segment, Segment); double get_dis_ss(Segment a, Segment b)//求线段之间距离 { if (intersect(a, b)) return 0.0; return min(min(get_dis_ps(a.p1, b), get_dis_ps(a.p2, b)), min(get_dis_ps(b.p1, a), get_dis_ps(b.p2, a))); } //b在a的 const int CC = 1;//逆时针方向 const int C = -1;//顺时针方向 const int OB = 2;//方向相反 const int OF = -2;//方向相同 |b|>|a| const int OS = 0;//方向相同 |a|>|b| inline int ccw(Point p1, Point p2, Point p3)//判断三点的位置关系 { Vector a = p2 - p1; Vector b = p3 - p1; if (cross(a, b) > eps) return CC; if (cross(a, b) < -eps) return C; if (dot(a, b) < -eps) return OB; if (norm(a) < norm(b)) return OF; return OS; } inline int ccw(Vector a, Vector b)//判断向量的位置关系 { if (cross(a, b) > eps) return CC; if (cross(a, b) < -eps) return C; if (dot(a, b) < -eps) return OB; if (norm(a) < norm(b)) return OF; return OS; } inline bool intersect(Point a, Point b, Point c, Point d)//判断两线段相交 { return ccw(a, b, c) * ccw(a, b, d) <= 0 && ccw(c, d, a) * ccw(c, d, b) <= 0; } inline bool intersect(Segment a, Segment b) { return intersect(a.p1, a.p2, b.p1, b.p2); } Point getCrossPoint_Line(Line s1, Line s2)//求两直线交点 { Vector v1, v2; v1 = s1.p2 - s1.p1, v2 = s2.p2 - s2.p1; Vector u = s1.p1 - s2.p1; double t = cross(v2, u) / cross(v1, v2); Point x = v1 * t; return s1.p1 + x; } Point getCrossPoint(Segment s1, Segment s2, bool flag = 0)//求两线段交点 { if (!intersect(s1, s2)) { if (flag) return getCrossPoint_Line(s1, s2); else return Point(1e18, 1e18); } Vector base = s2.p2 - s2.p1; double d1 = abs(cross(base, s1.p1 - s2.p1)); double d2 = abs(cross(base, s1.p2 - s2.p1)); double t = d1 / (d1 + d2); Point x = (s1.p2 - s1.p1) * t; return s1.p1 + x; } pair<Point, Point> getCrossPoint(Line l, Circle C)//求直线与圆交点 { if (get_dis(C.c, l) > C.r) return make_pair(Point(2e18, 2e18), Point(2e18, 2e18)); Point pr = project(C.c, l); Vector e = (l.p2 - l.p1) / abs(l.p2 - l.p2); double base = sqrt(C.r * C.r - norm(pr - C.c)); Vector x = e * base; return make_pair(pr + x, pr - x); } inline Polygon andrewScan(Polygon p)//求凸包 { Polygon u, d; if (p.size() < 3) return p; sort(p.begin(), p.end()); u.pb(p[0]); u.pb(p[1]); d.pb(p[p.size() - 1]); d.pb(p[p.size() - 2]); for (int i = 2; i < p.size(); i++) { for (int k = u.size(); k >= 2 && ccw(u[k - 2], u[k - 1], p[i]) != C; k--) u.pop_back(); u.pb(p[i]); } for (int i = p.size() - 3; ~i; i--) { for (int k = d.size(); k >= 2 && ccw(d[k - 2], d[k - 1], p[i]) != C; k--) d.pop_back(); d.pb(p[i]); } reverse(d.begin(), d.end()); for (int i = u.size() - 2; i; i--) d.pb(u[i]); return d; } inline bool cmp_ang(Segment a, Segment b)//极角排序 { return a.ang < b.ang; } inline bool OnLeft(Point p, Line s) { return cross(s.p2 - s.p1, p - s.p1) > 0.0; } inline Polygon HPI(vector<Segment> L)//求半平面交 { int n = L.size(); sort(L.begin(), L.end(), cmp_ang); int head, tail; vector<Point> p(n); vector<Segment> q(n); vector<Point> ans; q[head = tail = 0] = L[0]; for (int i = 1; i < n; i++) { while (head < tail && !OnLeft(p[tail - 1], L[i])) tail--; while (head < tail && !OnLeft(p[head], L[i])) head++; q[++tail] = L[i]; if (equals(cross(q[tail].p2 - q[tail].p1, q[tail - 1].p2 - q[tail - 1].p1), 0.0)) { tail--; if (OnLeft(L[i].p1, q[tail])) q[tail] = L[i]; } if (head < tail) p[tail - 1] = getCrossPoint(q[tail - 1], q[tail], 1); } while (head < tail && !OnLeft(p[tail - 1], q[head])) tail--; if (head == tail) return ans; p[tail] = getCrossPoint(q[tail], q[head], 1); for (int i = head; i <= tail; i++) ans.pb(p[i]); return ans; } inline double Ploygon_area(Polygon s)//求多边形面积 { int n = s.size(); double ans = 0.0; for (int i = 0; i < n; i++) { ans += cross(s[i], s[(i + 1) % n]); } return ans * 0.5; } int main() { return 0; }
扩展
三维向量的计算
向量的内积(点积)
$\vec a\cdot \vec b=x_ax_b+y_ay_b+z_az_b$
向量的外积(叉积)
$\vec a\times \vec b=(x_a,y_a,z_a)\times (x_b,y_b,z_b)=(y_az_b-z_ay_b,z_ax_b-x_az_b,x_ay_b-x_ay_b)$
求平面方程
已知三点$P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2),P_3(x_3,y_3,z_3)$(三点不在同一直线)
求过三点的平面$Ax+By+Cz+D=0$
$\vec{n}=\vec {P1P2}\times \vec {P1P3}=(A,B,C)$
求点在平面上的投影
求点$P(x,y,z)$在平面$Ax+By+Cz+D=0$上的投影$P'(x',y',z')$
$t=\frac{Ax+By+Cz+D}{A^2+B^2+C^2}$
$P'=(x-At,y-Bt,z-Ct)$
平面图面点线的关系
$F$ :面 $E$ :边 $V$ :点
$F-E+V=2$



 浙公网安备 33010602011771号
浙公网安备 33010602011771号