博弈论入门笔记

从小学奥数开始

给定一堆石子, 共n个石子，两个玩家轮流取石子, 每次只能拿1个或2个或3个石子. 不能取石子的一方输. 问先手有无必胜策略.

解:

当且仅当n不为4的倍数的时候, 先手有必胜策略.

我们可以将游戏的局面(即当前剩余的石子个数\(x\))分成两类, x%4==0和x%4!=0, 不妨分别称之为P局面(必败局面)和N局面(必胜局面).

当拿到N局面时,玩家可以将N局面改变成P局面; 当拿到P局面的时候, 玩家只能将P局面改成N局面. 最终\(x=0\)这个最终局面落在P局面.

如下图所示:

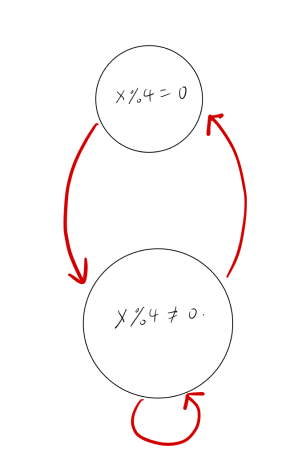
巴什博弈(Bash Game)

让我们对上面的小学奥数题进行推广.

给定一堆石子, 共n个. 两个玩家轮流取石子, 每次至少取一个, 至多取m个. 不能取石子的输. 问给定n, m, 先手是否有必胜策略.

解:

当且仅当, n不为(m+1)的倍数时, 先手有必胜策略. 推理过程如上.

尼姆博弈(Nim Game)

给定n堆石子. 每堆石子有\(a_i\)个石子. 两个玩家轮流取石子. 每回合选定一个堆, 至少取一个石子, 至多把选定的这一堆石子取完. 无法取石子的一方判负. 问, 给定n和数组a, 先手是否有必胜策略.

解:

请先了解异或操作.

直接给出结论: 当且仅当, n堆石子的异或和不等于0时, 先手有必胜策略.

我们考虑上面的小学奥数题, 我们把整个游戏的局面抽象成了两种, 并且让必败局面的后继有且仅有必胜局面.

受到这个的启发, 我们尝试将尼姆博弈的局面也抽象成两种. 即, 石子堆的异或和为0 和 不为0.

让我们称异或和为0时, 为必败局面; 异或和不为0时, 为必胜局面.

我们有以下三点性质:

1. 最终局面, 即没有石子可取的时候, 所有石子堆的石子数都为0, 所以异或和自然也为0. 也就是说, 最终局面可以被纳入必败局面中.
2. 石子堆的异或和为0时, 无论在一个石子堆种取多少石子, 异或和都不会为0. 由异或的性质不难得出.
3. 石子堆的异或和不为0时, 总有一种取法, 使得取完之后异或和为0. 由异或的性质不难得出.

于是, 归纳一下, 我们得出下图:

Note: 尼姆博弈是十分重要的, 很多博弈都可以转换成尼姆游戏的变形. 实际上, 所有公平组合游戏都可以看成尼姆博弈的变形.

反尼姆博弈(Anti-Nim Game)

给定n堆石子. 每堆石子有\(a_i\)个石子. 两个玩家轮流取石子. 每回合选定一个堆, 至少取一个石子, 至多把选定的这一堆石子取完. 取到最后一个石子的一方判负. 问, 给定n和数组a, 先手是否有必胜策略.

解:

我们看到反尼姆博弈和尼姆博弈的唯一区别点就是, 最后的胜利条件是相反的.

同样先给出结论再证明:

先手有必胜策略, 当且仅当:

1. 所有堆的石子数都为1, 且异或和为0.
2. 或者, 至少有一堆石子数大于1, 且异或和不为0

条件1的正确性是显然的, 当条件1成立的时候, 场上有偶数堆石子数为1的石子, 一人一个, 自然先手获胜.

对于条件2, 也就是至少有一堆石子数大于1, 我们分两种情况来讨论

1. 当异或和不为0时: 若还有两堆石子数目大于1, 我们把异或和变为0; 若只有一堆石子数目大于1, 我们总可以使得场上只剩下奇数堆的1.
2. 当异或和为0时, 无论怎么取, 异或和总不为0. 注意, 由异或的性质可得 ,异或和为0时, 至少有两堆石子数目大于1.

状态转移如下图所示:

公平组合游戏

当且仅当下列条件全部满足的时候, 是公平组合游戏:

1. 游戏有两个人参与, 两人轮流做出决策, 双方都知道游戏的完整信息.
2. 任意一个游戏者在某一个确定状态下可以做出的决策集合只与当前状态有关, 与游戏者无关.
3. 游戏中的一个状态不可以多次抵达, 游戏以玩家无法移动结束.
4. 游戏一定在有限步内结束, 没有平局.

上面讨论的巴什博弈, 尼姆博弈, 反尼姆博弈都是公平组合游戏.

有的同学可能有疑惑, 上面的三种博弈模型中, 同一个状态被多次到达了, 貌似违反了一个状态不能多次到达的定义.

其实不是的, 上面的状态实际上是某一群特定状态的集合. 例如在巴什博弈中, \(n=13\)是一个确定状态, 而\(n\%(m+1)=0\)是一类特定状态.

公平组合游戏都可以用\(SG\)函数求解，因此又称为\(SG\)组合游戏。

SG函数

下面介绍公平组合游戏中的一个非常有用的工具——SG函数。

SG函数是对博弈中的每个状态（节点）的评估函数，定义如下：

\(sg(v) = mex \{sg(u)|状态u是状态v的后继\}\)

其中\(mex(S)\)函数的意义为，不属于集合\(S\)的最小非负数。

当且仅当，某个状态的SG函数为0时，该状态必败。

这看起来十分地抽象，我们不妨以SG函数来分析我们熟悉的Nim博弈看看。

再探Nim博弈

我们首先来考虑特殊形况下的尼姆博弈——只有一堆石子的尼姆博弈。

当我们有一堆石子，记这一堆石子的总数为\(a_1\)。我们可以发现，这一堆石子的后继是\(\{0,1,2,...,a_1-1\}\)，不难发现单堆石子的SG函数就是该堆石子的石子数。

接着，我们给出一个定理：

SG定理：

如果一个游戏等价于，若干个公平组合游戏同时进行且每次只能对某个公平组合游戏进行单次操作，那么，该游戏的某个局面的SG函数等于其所有子游戏的SG函数的异或和。

根据SG定理，我们不妨将一般的尼姆博弈看作若干个只有一堆石子的尼姆博弈，这时整个游戏的SG函数等于所有堆石子数的异或和。

于是，我们从SG函数的角度将Nim游戏又推了一遍。

我的理解是：SG函数就是将一个公平组合游戏抽象成Nim游戏的工具。

阶梯尼姆

问题引入：

A和B喜欢玩博弈游戏。他们在一个阶梯上的层阶都放上了若干个石子（\(\ge 0\))。现在A和B轮流进行以下操作：选定阶梯上的任意一层，然后移动至少一个石子到相邻的较低层。无法进行操作（所有的石子都被移动到了地板上）的人输掉游戏。给定一个初始状态，问谁赢？（试求\(O(n)\)的算法）

例，给定五个层的阶梯，从高到低分别由5，4，3，2，1个石子，如下图。

分析：

这个问题可以通过适当的变形成为尼姆博弈。

考虑必胜策略如下：

当奇数层的石子数的异或和不为0时，先手胜。

这是因为如果奇数层的石子数的异或和不为0时，先手可以一步使得其为0。

如果遇到奇数层石子数的异或和为0时，不论是加（将偶数层的石子移到奇数层），还是减（将奇数层的石子移到偶数层或者地面），都不能做到维持石子数的异或和为0.

不难看出这是和尼姆游戏一个概念的东西。

例题：

POJ1704

简述：

A和B玩游戏。在一个\(1*n\)的棋盘上共有m个棋子，A和B轮流进行操作：选择一个棋子，并向又移动，不允许跨过任何棋子和移出棋盘。

分析：

我们把每个棋子目前所能走的步数单独拿出来做为一个数组b，不难看出，进行一次操作就是将前一枚棋子可走的步数让渡给下一枚棋子，这是标准的阶梯尼姆。

于是我们通过适当变形即可将本题化为阶梯尼姆。

代码：

#include <iostream>
#include <algorithm>
#include <stdio.h>
using namespace std;
const int N = 2005;
int a[N];
void solve()
{
    int n; scanf("%d",&n);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    sort(a+1, a+n+1);
    for(int i = n; i; i--) a[i] = a[i] - a[i-1] - 1;
    int sum = 0;
    for(int i = n; i > 0; i -= 2) sum ^= a[i];
    if(sum == 0) printf("Bob will win\n"); // 先手败
    else printf("Georgia will win\n"); //先手胜
}
int main()
{
    int T; scanf("%d",&T);
    while(T--) solve();
    // system("pause");
}

斐波那契博弈

问题引入：

取石子

1堆石子有n个,两人轮流取.先取者第1次可以取任意多个，但不能全部取完.以后每次取的石子数不能超过上次取子数的2倍。取完者胜.先取者负输出"Second win".先取者胜输出"First win".

分析：

观察发现，当n为斐波那契数时，先手必败。

证明如下：

设n为第i位斐波那契数，记为\(f_i\).

• 当\(f_i\le 2\)时，先手必败。
• 当\(f_i>2\)时，不妨设\(n=f_{i-1}\)和\(n=f_{i-2}\)必败. 考虑：\(f_i = f_{i-1}+f_{i-2}, f_{i-1} \le 2f_{i-2}\)
  1. 此时先手不能取大于等于\(f_{i-2}\)个石子, 否则后手可以一步取完。
  2. 因此问题转化为对于\(f_{i-2}\)个石子，先手能否取到最后一个？显然是不行的，因为根据定义\(f_{i-2}\)先手必败。

证毕。

接下来考虑证明n不为斐波那契数时，先手必胜。

证明：

首先给出一个定理:

齐肯多夫定理(Zeckendorf's theorem)：任何正整数n可以被表示成若干个不连续的斐波那契数之和。

证明如下：

• 当n为斐波那契数时，定理显然成立。

• 当n不为斐波那契数时，不妨设对于\(i<n\), 定理都成立（这是因为斐波那契数列\(f_1,f_2,f_3\)分别为1，2，3）。

  设\(n'=n-f_m\), 其中\(f_m\)为最大的小于n的斐波那契数。

  根据假设，\(n'\)可以表述成若干个不连续的斐波那契之和，且\(n'<f_{m-1}\)， 故其不连续的斐波那契数中不包含\(f_{m-1}\)。不妨记\(n'\)的斐波那契表示为\(F(n')\)

  故，\(F(n) = f_m+F(n')\)

证毕

记\(n = f_{s_1}+f_{s_2}+....+f_{s_k}\) , 即把n做为k个不连续的斐波那契数的和，其斐波那契数列的下标做为集合s， 其中\(s1<s_2<...<s_k\)。

给出一个构造方法：

1. 先手取当前最小的斐波那契数\(f_{s_1}\)

2. 后手显然只能取不完剩下的次小的斐波那契数\(f_{s_2}\)(\(f_i\gt 2f_{i-2}\))

   那么可以看作以后手为先手的，取这个次小的斐波那契数\(f_{s_2}\)的子问题(即形式上与原问题一样，但规模比原问题小)。

   考虑之前已经证明过n为斐波那契时先手必败，那么对于这个子问题，原问题的先手可以取到\(f_{s_2}\)最后一块石子。

   于是对于之后所有的\(f_{s_i},i\gt2\), 都可以类似地考虑。也就是对于每个\(f_{s_i}\)子问题，原问题的先手总是取到最后一个石子。

证毕。

代码

#include <bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define close(); 	ios::sync_with_stdio(false);
#define endl '\n'
#define rep(i, l, r) for(int i = l; i <= r; i++)
#define dwn(i, r, l) for(int i = r; i >= l; i--)
typedef long long LL;
const int N = 3e5+100;
LL a[N];
int cnt;
void init()
{
    a[0] = a[1] = 1;
    cnt = 1;
    rep(i, 2, 100)
    {
        a[i] = a[i-1] + a[i-2];
        ++cnt;
        if(a[i] >= (1ll<<31)) break;
    }
}

void solve(LL n)
{
    auto p = lower_bound(a+1, a+cnt+1, n);
    if(*p == n) cout << "Second win\n";
    else cout << "First win\n";
}

int main()
{
    init();
    LL n; cin >> n;
    while(n) 
    {
        solve(n);
        cin >> n;
    }
    // system("pause");
}

威佐夫博弈

问题引入

洛谷P2252：

有两堆石子，数量任意，可以不同。游戏开始由两个人轮流取石子。游戏规定，每次有两种不同的取法，一是可以在任意的一堆中取走任意多的石子；二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目，你先取，假设双方都采取最好的策略，问最后你是胜者还是败者。

分析：

已知初始情况a，b不同时为0。

定义： 后手有必胜策略的局势，称之为奇异局势。

观察得出第\(0\)种奇异局势(0,0)，当a,b一方为零或者a与b的差值为0时可以一步到达(0,0)。

当选手观察到奇异局势(0,0)时，表示对手已经取完石子，已经胜利。

继续观察，得出第\(1\)种奇异局势(1,2)，当a,b一方为2或者1时；a，b差值为1时,可以一步到达(1,2)。

当玩家观察到奇异局势(1,2)时，有四种行动方案：

1. \((1,2) \rightarrow (1,1)\)
2. \((1,2) \rightarrow (1,0)\)
3. \((1,2) \rightarrow (0,1)\)
4. \((1,2) \rightarrow (0,2)\)

我们发现，不论选择哪种行动，后手玩家都可以一步将其转移到第\(0\)种奇异局势，导致先手玩家的必败。

不妨继续观察，得到第\(2\)种奇异局势(3,5)，当a,b一方为\(3\space or \space 5\)时 或者 当a与b差值为2时，可以一步到达(3,5)。

当局势是(3,5)时，可以大致分为 \(3\) 种行动方案：

1. 缩小a，b的差值。此时差值为2，缩小差值意味着差值的大小将变为 0 或者 1。如此一来，对方可以一步使局势进入第0, 1种奇异局势。
2. 扩大a，b的差值。显然是要取3个石子的那堆，也就是这堆石子将会变为\({0,1,2}\)。如此一来，对方可以一步使局势进入第0, 1种奇异局势。
3. 维持a，b差值不变。为此需要执行第二种操作，也就是两堆石子一起取相同数字的石子走掉。操作完后，较小的数字将会在\({0,1,2}\)中。如此一来，对方可以一步使局势进入第0, 1种奇异局势。

因此局势(3,5)是奇异局势。

到此我们似乎发现了奇异局势的一些规律，比如：

1. 奇异局势无法在一次且仅为操作内取完。(0,0)也是，因为无法进行一次操作，此时对方已经获胜。

2. 当玩家遇到第\(i\)个奇异局势时，无论玩家如何操作，对方可以让该玩家在下一回合遇到第\(j(j<i)\)种奇异局势。因此遇到奇异局势可以恒等于失败。

3. 观察奇异局势之间的转移似乎基于两种机制。记奇异局势为\((x,y) \space 且 \space x<y\)

   • 缩小差值。如局势(3,5)的第一种行动方案。
   • 减小较小值。如局势(3,5)的第2，3种方案。

   也就是说我们要保证奇异局势可以向下转移，要保证两种机制的实现。

   机制一的保证：较高层的奇异局势\((x,y)\)的差值\(y-x\)需要比 比其低层的奇异局势的最大差值 多且仅多\(1\)。因为如果相等就没有意义，如果大于1则不能保证转移。

   机制二的保证：较高层的奇异局势\((x,y)\)的两个值\(x,y\)不能与 较其低层的奇异局势的值 相等。因为如果存在相等，就可以一步转移到另一种奇异局势，导致对方必败，与奇异局势的定义相悖。

搞明白这些规律之后我们就可以来构造更多的奇异局势来找更多的规律了。

对于第\(i\)个奇异局势\((x,y)\)具体的构造方法是：

1. 第\(0\)个奇异局势是\((0,0)\)。
2. \(x\)选定为第[0, i)个奇异局势中 未曾出现的最小非负整数。
3. \(y = x +i\)

以下是其他的奇异局势：

	第3种奇异局势 (4,7)

	第4种奇异局势 (6,10)

	第5种奇异局势 (8, 13)

	第6种奇异局势 (9, 15)

	第7种奇异局势 (11, 18)

	……

我们通过上面的构造又可以总结出几条结论：

1. 任何自然数都包含在且仅包含在一个奇异局势中。
2. 任意操作都会使奇异局势转移成非奇异局势
3. 通过适当的方法，可以将非奇异局势转换成奇异局势
4. 一个局势，要么为非奇异局势，要么为奇异局势

如图：

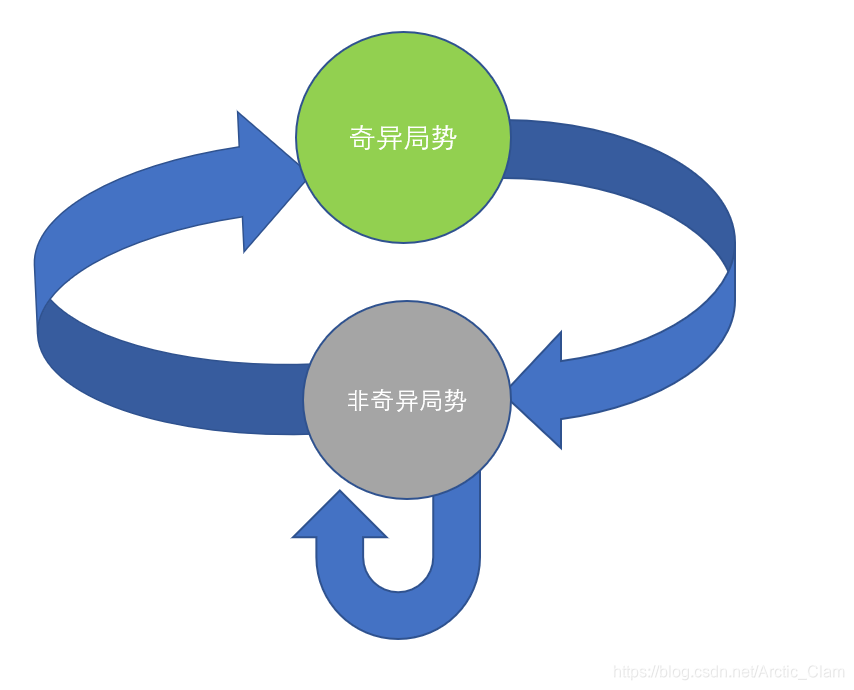
好了，现在我们离解出这道题很近了，我们只需要判断题目给出的\(a,b\)是否是奇异局势就好了。

但是数据范围很大，递推的方式毫无疑问会超时。

其实我们有一个很好用的公式：

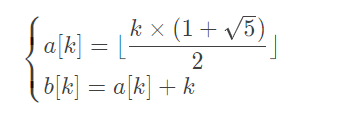
其中a[k]表示第k个奇异局势的a，b[k]表示第k个奇异局势的b，其中k为自然数。

证明如下：

首先我们有Beatty定理：

设a、b是正无理数且 \(\frac{1}{a} +\frac{1}{b} =1\)。记\(P=\{ \lfloor na \rfloor | n为任意的正整数\}，Q=\{ \lfloor nb \rfloor | n 为任意的正整数\}\)，则P与Q是\(N^+\)的一个划分，即\(P∩Q=\varnothing\)且\(P∪Q=N^+\)（正整数集）。

回顾我们之前的这个结论：

任何自然数都包含在且仅包含在一个奇异局势中。且a,b不相同的情况下，也就是说全体奇异局势(不包含\((0,0)\))的a的集合A和b的集合B也是正整数的一个划分。

我们尝试用一个无理数\(\lfloor ku\rfloor\)来表示a，一个无理数\(\lfloor(u+1)k\rfloor\)来表示b，其中k表示第k个奇异局势，同时\(b-a=n\)符合定义，其中k为正整数。

也就是说我们有\(\frac{1}{u}+\frac{1}{u+1}=1\)。解这个方程得出\(u = \frac{1+\sqrt{5}}{2}\)。

同时将\((0,0)\)带入，k=0, 因此k可以等于0。

Q.E.D

代码实现

#include <iostream>
#include <cmath>
using namespace std;
int a, b;
const double lorry = (sqrt(5.0) + 1.0) / 2.0;

int main() {
    cin >> a >> b;
    if(a < b) swap(a, b);
    int k = a - b;
    if(b == int(lorry * k))
        cout << 0 << endl;
    else 
        cout << 1 << endl;
}