计算几何技巧

基础知识

• 点积：$\vec{P}\cdot \vec{Q}=|P||Q|cos\theta=x_1x_2+y_1y_2$

  • 几何意义 $\vec{P}$在$\vec{Q}$上的投影与$\vec{Q}$的长度的乘积。

  • 应用：

    判断两个向量是否垂直：$\vec{P}⊥\vec{Q} \iff \vec{P}\cdot \vec{Q}=0$

    求两个向量的夹角：$\theta=acos(\frac{\vec{P}\cdot \vec{Q}}{|\vec{P}||\vec{Q}|})$，若$\vec{P}\cdot \vec{Q}\lt 0$为钝角，$\vec{P}\cdot \vec{Q} \gt 0$为锐角

• 叉积：$\vec{P}\cdot \vec{Q}=|P||Q|sin\theta=x_1y_2-x_2y_1$

  • 几何意义：$\vec{P}$与$\vec{Q}$张成的平行四边形的有向面积。$\vec{Q}$在$\vec{P}$的逆时针方向为正。

  • 应用：

    假如$\vec{P}$在$\vec{Q}$的左边，则有向面积为正，假如在右边则为负。假如$\vec{P},\vec{Q}$共线，则叉积为$0$。

• 直线相关

  • 直线的表现形式：

    一般形式：$ax+by+c=0$

    点向式：$p_0+\vec{v}t$

    斜截式：$y=kx+b$

• 多边形

  • 面积：

    叉积计算

    海伦公式(已知边长计算三角形面积)：$p=\frac{(a+b+c)}{2}$，则$S=\sqrt{p(p-a)(p-b)(p-c)}$

    皮克定理：指一个计算点阵中顶点在格点上的多边形面积公式该公式可以表示为$S = a + \frac{b}{2} - 1$，其中$a$表示多边形内部的点数，$b$表示多边形边界上的点数，$S$表示多边形的面积。

    辛普森积分：对于一个二次函数$f(x)=Ax^2+Bx+C$，有$\int{l}{r}f(x)dx=\frac{(r-l)f(l)+f(r)+4f(\frac{l+r}{2})}{6}$。如果不是二次函数，就每次细分，最后细分到一定程度这部分的面积就可以套用这个二次函数的面积公式。

  • 三角形的四心：

    外心：外接圆圆心，三边中垂线交点，到三角形三个顶点的距离相等

    内心：内切圆圆心，角平分线交点，到三边距离相等

    垂心：三条垂线交点

    重心：三条中线交点（到三角形三顶点距离的平方和最小的点，三角形内到三边距离之积最大的点）

• 体积

  • 球的体积交，设两球的半径分别为$R_1,R_2$（$R_1\le R_2$），球心间距$d$

    • $d\ge R_1+R_2$：两球不相交，$V=0$

    • $d+R_1=R_2$：小球在大球里面，$V=\frac{4}{3}\pi(R_1)^3$

    • $R_2-R_1\lt d\lt R_2+R_1$：

      $$设cos\alpha=\frac{R_2^2+d^2-R_1^2}{2R_2d},h_1=R_2(1-cos\alpha)\\ cos\beta=\frac{R_1^2+d^2-R_2^2}{2R_1d},h_2=R_1(1-cos\beta)\\ V=\frac{\pi}{3}(3R_2-h_1)h_1^2+\frac{\pi}{3}(3R_1-h_2)h_2^2$$

• 凸包

  • 判断点是否在凸包上

• 半平面交

  • 一条直线把一个平面划分成两个部分，如果把一个$n$个点凸包的每条边按照逆时针连接，并按照顺序给每条边一个方向，那么凸包可以看做是这$n$条有向直线的左半平面交

• 最小圆覆盖

  • 最小覆盖圆是唯一的
  • 若 $p$不在 $S$ 的最小覆盖圆内部，则 $p$ 必在$\{p\}∪S$的最小覆盖圆边上

• 旋转卡壳

  • 对踵点对

  • 求解问题：

    • 计算距离
      • 凸多边形直径
      • 凸多边形宽
      • 凸多边形间最大距离
      • 凸多边形间最小距离
    • 外接矩形
      • 最小面积外接矩形
      • 最小周长外界矩形

闵可夫斯基和

• 点集$A,B$，则$C=\{p_1+p_2 | p_1\in A,p_2\in B \}$，则$C$称为$A$和$B$的闵可夫斯基和
• 先求形状，最后图形的形状是两个多线性的边界向量排序后按照顺序相接，即把两凸包的边向量极角排序后按照逆时针顺序相连
• 两条凸包的闵可夫斯基和也是凸的

JSOI2018

Problem

给定两个凸包$A,B$，每次给定一个方向向量$\vec{v}$，问凸包$A$沿着$\vec{v}$移动后是否会和$B$有交。

Solve

$p_1\in A,p_2\in B$，则有交说明$v+p_1=p_2$，等价于$v=p_2-p_1$，把$A$取反后和$B$求闵可夫斯基和判断$v$是否在所形成的的凸包里面即可。

Code

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+10;
struct Point{
    ll x,y;
    Point operator + (const Point &t)const{
        return Point{x+t.x,y+t.y};
    }
    Point operator - (const Point &t)const{
        return Point{x-t.x,y-t.y};
    }
    ll operator ^ (const Point &t)const{ //叉积
        return x*t.y-y*t.x;
    }
    ll len(){
        return x*x+y*y;
    }

}A[N],B[N];
int n,m,q;
bool cmp1(Point a,Point b){
    return a.x==b.x?a.y<b.y:a.x<b.x;
}
bool cmp2(Point a,Point b){
    return (a^b)>0||((a^b)==0&&(a.len()<b.len()));
}
Point stk[N];
int top;
void Convex(Point P[],int &n){
    sort(P+1,P+1+n,cmp1);
    Point base=P[1];
    for(int i=1;i<=n;i++) P[i]=P[i]-base;
    sort(P+2,P+1+n,cmp2);
    stk[top=1]=P[1];
    for(int i=2;i<=n;i++){
        while(top>=2&&((stk[top]-stk[top-1])^(P[i]-stk[top-1]))<=0) top--;
        stk[++top]=P[i];
    }
    n=top;
    for(int i=1;i<=n;i++)P[i]=stk[i]+base;
}
Point s1[N],s2[N],C[N];
int tot;
void Minkowski(){
    for(int i=1;i<n;i++) s1[i]=A[i+1]-A[i];s1[n]=A[1]-A[n];
    for(int i=1;i<m;i++) s2[i]=B[i+1]-B[i];s2[m]=B[1]-B[m];
    C[tot=1]=A[1]+B[1];
    int l=1,r=1;
    while(l<=n&&r<=m) ++tot,C[tot]=C[tot-1]+((s1[l]^s2[r])>=0?s1[l++]:s2[r++]);
    while(l<=n) ++tot,C[tot]=C[tot-1]+s1[l++];
    while(r<=m) ++tot,C[tot]=C[tot-1]+s2[r++];
}
bool point_in_conve(Point x){
    if((x^C[1])>0||(x^C[tot])<0) return 0;
    int id=lower_bound(C+1,C+1+tot,x,cmp2)-C-1;
    return ((x-C[id])^(C[id%tot+1]-C[id]))<=0;
}
int main(){
     ios::sync_with_stdio(false);
     cin.tie(nullptr);
     cin>>n>>m>>q;
     for(int i=1;i<=n;i++) cin>>A[i].x>>A[i].y;
     for(int i=1;i<=m;i++) cin>>B[i].x>>B[i].y,B[i].x=-B[i].x,B[i].y=-B[i].y;
     Convex(A,n);
     Convex(B,m);
     Minkowski();
     Convex(C,tot);
     Point base=C[1];
     for(int i=1;i<=tot;i++) C[i]=C[i]-base;
    while(q--){
        Point p;
        cin>>p.x>>p.y;
        cout<<point_in_conve(p-base)<<'\n';
    }
}

反演

• 内容：反演中心为$O$，反演半径为$R$，若经过$O$的直线经过$P,P^{'}$，且$|OP||OP^{'}|=R^2$，则称$P、P^{'}$关于$O$互为反演
• 性质：
  • 一根过$O$的直线的反演是本身
  • 一根不过$O$的直线的反演是一个过$O$的圆
  • 一个过$O$的圆的反演是一根不过$O$的直线
  • 一个不过$O$的圆的反演是一个和该圆关于$O$位似的圆
  • 反演不改变相切关系

• 反演代码
  • 不过反演中心的圆的反演

    Circle Inv_C2C(Point O,double R,Circle A) //反演中心，反演半径，反演圆
    {
    	double OA=(A.c-O).len();
    	double RB=0.5*((1/(OA-A.r)-(1/(OA+A.r))))*R*R;
    	double OB=OA*RB/A.r;
    	double Bx=O.x+(A.c.x-O.x)*OB/OA;
    	double By=O.y+(A.c.y-O.y)*OB/OA;
    	return Circle({Bx,By},RB);
    }
    

  • 不过反演中心的直线反演成圆

    Circle Inv_L2C(Point O,double R,Point A,Point v){  //直线反演成圆，点向式表示直线
        Point P=GetLineProjection(O,A,A+v);
        double d=(O-P).len();
        double RB=R*R/(2*d);
        Point VB=(P-O)/d*RB;
        return Circle(O+VB,RB);
      }
    

HDU 4473 [Problem of Apollonius]

Problem

求过两圆外一点，且与两圆相切的所有的圆。

Solve

以所给点$P$为反演中心，原来的两个圆反演后还是圆，所求的圆反演后是直线，问题就变成了求与反演后的圆相切的全部直线，这样的直线最多$4$条，求出直线后再对直线反演成圆即可。

两点确定一条直线，切线用两个点来表示，最后切线用点向式表示
切点用极坐标的方式求
外切计算切线的两个点


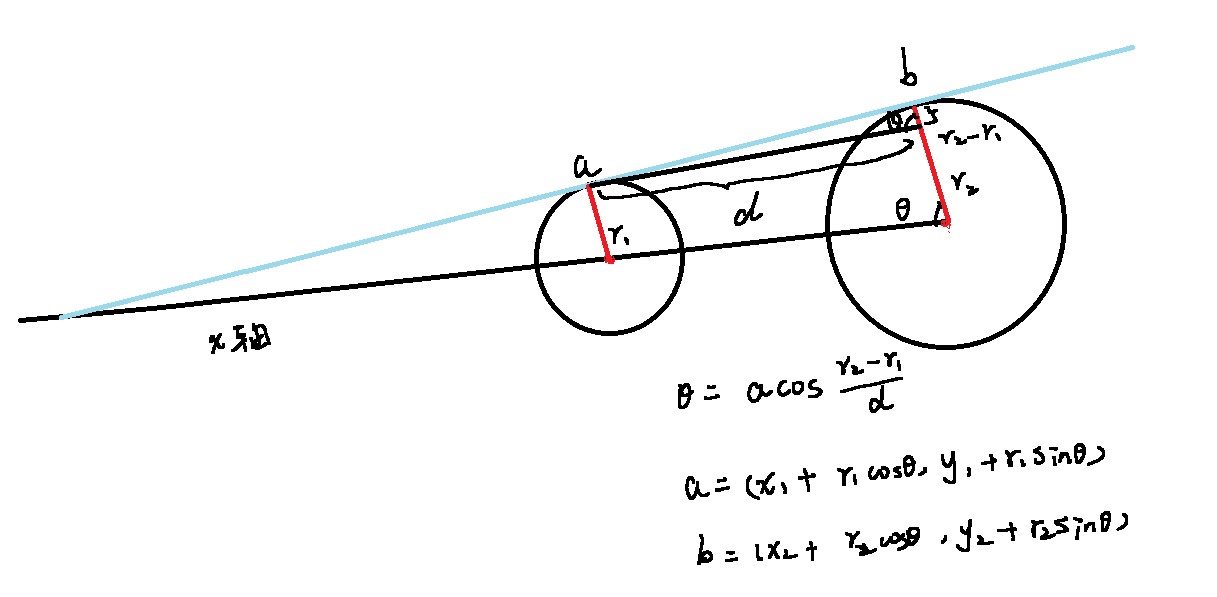
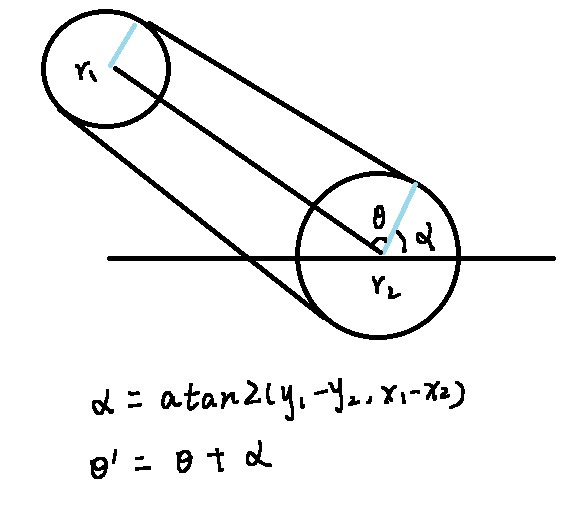
内切计算切线的两个点

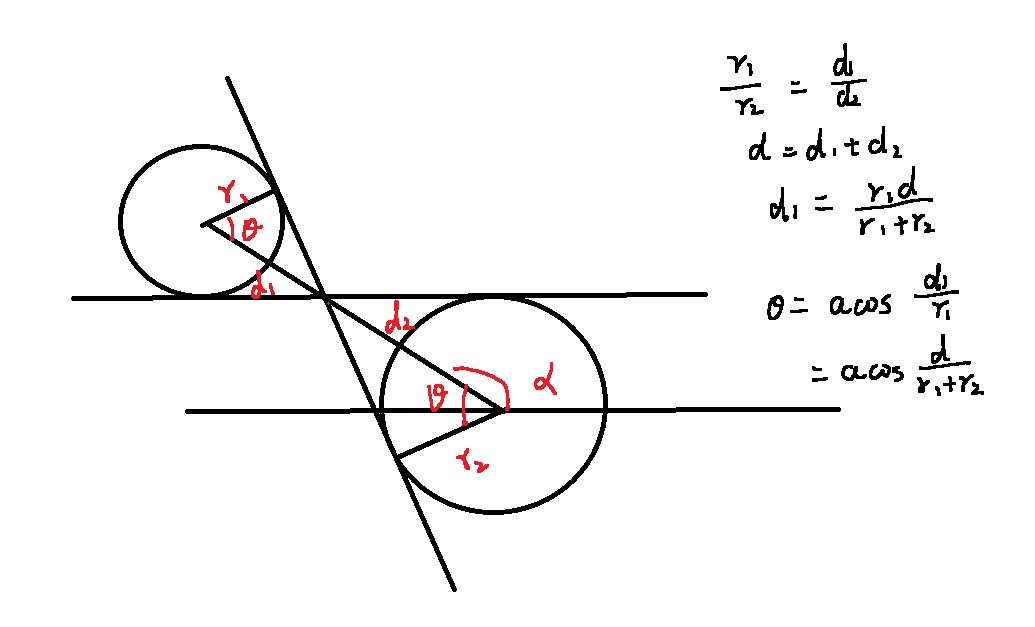
判断两个点是否在直线的同一侧用叉积判断

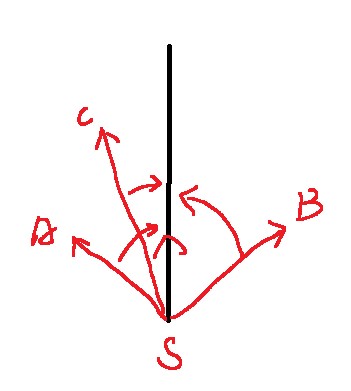
Code

#include <iostream>
#include <cmath>
#include <algorithm>
#include <iomanip> 
using namespace std;
const double eps=1e-8;
const double PI=acos(-1);
int dcmp(double x,double y){
    if(fabs(x-y)<eps) return 0;
    else if(x<y) return  -1;
    else return 1;
}
struct Point{
     double x,y;

     Point operator + (const Point &t) const{
        return {x+t.x,y+t.y};
     }
     Point operator - (const Point &t) const{
        return {x-t.x,y-t.y};
     }
     double operator * (const Point &t) const{
        return x*t.x+y*t.y;
     }
     Point operator * (const double &t) const{
        return {x*t,y*t};
     }
     Point operator / (const double &t) const{
        return {x/t,y/t};
     }
     double operator ^ (const Point &t) const{
        return x*t.y-y*t.x;
     }
     double len(){
        return sqrt(x*x+y*y);
     }
};
struct Circle{
    Point c;
    double r;
    Circle():c({0,0}),r(0){};
    Circle(Point c,double r):c(c),r(r){}

    Point point(double a){//用极坐标求圆上点的坐标
        return {c.x+cos(a)*r,c.y+sin(a)*r};
    }
};
//反演
Circle Inv_C2C(Point O,double R,Circle A) //反演中心，反演半径，反演圆
{
    double OA=(A.c-O).len();
    double RB=0.5*((1/(OA-A.r)-(1/(OA+A.r))))*R*R;
    double OB=OA*RB/A.r;
    double Bx=O.x+(A.c.x-O.x)*OB/OA;
    double By=O.y+(A.c.y-O.y)*OB/OA;
    return Circle({Bx,By},RB);
}
//点在直线上的投影
Point GetLineProjection(Point P, Point A, Point B) {
  Point v = B - A;
  return A + v*((v*(P - A)) / (v*v));
} 
Circle Inv_L2C(Point O,double R,Point A,Point v){  //直线反演成圆，点向式表示直线
        Point P=GetLineProjection(O,A,A+v);
        double d=(O-P).len();
        double RB=R*R/(2*d);
        Point VB=(P-O)/d*RB;
        return Circle(O+VB,RB);
}
//用两点确定一个直线
int getTangents(Circle A,Circle B,Point a[],Point b[]){
    int cnt=0;
    if(A.r<B.r){
        swap(A,B);
        swap(a,b);
    }
    double d=(A.c-B.c).len();
    double Lr=A.r-B.r;
    double Rr=A.r+B.r;
    //内含
    // cout<<d<<" "<<Lr<<'\n';
    if(dcmp(d,Lr)==-1) return 0;
    double base=atan2(B.c.y-A.c.y,B.c.x-A.c.x);
    //两个圆相等，无数条
    if(dcmp(d,0)==0&&dcmp(Lr,0)==0) return -1;
    //内切
    if(dcmp(d,Lr)==0){  //A,B圆心连线上与A,B的两个交点
       a[cnt]=A.point(base);
       b[cnt]=B.point(base);
       ++cnt;
       return 1;
    }
    //外切
    //两条外公切线
    double ang=acos(Lr/d);
    a[cnt]=A.point(base+ang);
    b[cnt]=B.point(base+ang);
    ++cnt;
    a[cnt]=A.point(base-ang);
    b[cnt]=B.point(base-ang);
    ++cnt;

    //一条内公切线
    if(dcmp(d,Rr)==0){
        a[cnt]=A.point(base);
        b[cnt]=B.point(PI+base);
        ++cnt;
    }else if(dcmp(d,Rr)==1){
        double ang=acos(Rr/d);
        a[cnt]=A.point(base+ang);
        b[cnt]=B.point(PI+base+ang);
        cnt++;
        a[cnt]=A.point(base-ang);
        b[cnt]=B.point(PI+base-ang);
        cnt++;
    }
    return cnt;
}
//判断A,B两点是否在直线同侧
bool theSameSideOfLine(Point A,Point B,Point S,Point v){
    return dcmp((A-S)^v,0)*dcmp((B-S)^v,0)>0;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin>>T;
    while(T--){
       Circle A,B;
       Point P;
       cin>>A.c.x>>A.c.y>>A.r;
       cin>>B.c.x>>B.c.y>>B.r;
       cin>>P.x>>P.y;
       Circle invA=Inv_C2C(P,10,A);
       Circle invB=Inv_C2C(P,10,B);
       // cout<<invA.c.x<<" "<<invA.c.x<<" "<<invA.r<<'\n';
       // cout<<invB.c.x<<" "<<invB.c.x<<" "<<invB.r<<'\n';
       Point LA[4],LB[4];
       Circle ansC[4];
       int q=getTangents(invA,invB,LA,LB);
       int ans=0;
       for(int i=0;i<q;i++){
          if(theSameSideOfLine(invA.c,invB.c,LA[i],LB[i]-LA[i])){
            if(!theSameSideOfLine(P,invA.c,LA[i],LB[i]-LA[i])) continue;
            ansC[ans++]=Inv_L2C(P,10,LA[i],LB[i]-LA[i]);
           }
       }
       cout<<ans<<'\n';
       for(int i=0;i<ans;i++)
        cout<<fixed<<setprecision(10)<<ansC[i].c.x<<" "<<ansC[i].c.y<<" "<<ansC[i].r<<'\n';
    }
}

HDU 6158

关键点思想 1

• 计算几何中涉及到的变量往往是连续的
  • 行走的距离、转弯的角度等
• 因此，最优化问题中，方案集合$S$通常是无穷的
• 找到有限集$S^{'}$满足：
  • 包含最优解
  • 所有元素都是合法解或者所有非法解都能被排除

Tokyo2014 H

多校 2018 9E

关键点思想 2

• 计算几何中经常会遇到分段函数
  • 沿着折线行走时，对一个点的距离
• 虽然整体复杂，但是每一段都是简单函数
  • 线性函数、二次函数、凸函数
• 找到分界点的一个超集，分段考虑

WF 2015B

WF 2012A

HDU 4785

WF2017A