力扣 题目10-正则表达式匹配 上--几个动态规划思想例题的详解

  • 力扣原题目

  • 刚才有个朋友问我发生什么事了，我说怎么回事，给我发了几张截图。

  •  我一看！嗷！原来是昨天，有两个年轻人。

  • 三十多岁，一个体重，九十多公斤，一个体重八十多公斤。
  • 他们用正则表达式函数直接解决了这道题
  • 这两个年轻人不讲武德，来骗！来偷袭，力扣。这好吗？这不好！
  • 我劝！这位年轻人好自为之，好好反思，以后不要再犯这样的聪明，小聪明，啊，呃…程序员要以和为贵，要讲武德，不要搞窝里斗。

  • 不开玩笑了啊这题暴力肯定是可以解的 但是太麻烦 我一看题解好家伙 动态规划

  • 一年前学的早忘记了 我赶忙去复习了一波动态规划 然后做了几道题写一下过程

  • 至于上面的第10题的解答等下篇再说

  • 题目一

  • 如果一个奇葩国家的钞票面额分别是1、5、11，我们需要凑出15 并且用的钱张数最小--出自 https://www.zhihu.com/question/23995189(动态规划可以看这个学习一下)

  • 题解

  • 先写状态转移方程  n是剩下的钱数 f(n)就是张数

  • f(n)=min(f(n-1),f(n-5),f(n-11))+1;

  • 拿15举例 f(15)=min(f(14),f(10),f(4))+1 就是说我们想要找到15最少张数就要找到 14/10/4中最少的那张然后 14/10/4也要和15一样分别去分 直到为1的时候停止

  • 然后我们可以写成这样的代码 cost = min(cost, f[i - 1] + 1)  cost是一个很大的值 而f[i - 1] + 1是在上一次拿了一张一元的张数+1   5/11同理 然后从1往11判断得到最小(用一个数组全部存起来 具体看代码)

  • 代码

  • #include<iostream>
#include<string>
using namespace std;
int main() {
    int n,i,cost;
    int f[105];
    cin >> n;
    f[0] = 0;
    for (i = 1; i <=n; i++) {
        cost = INT_MAX;
        if (i - 1 >= 0) { cost = min(cost, f[i - 1] + 1) ;}
        if (i - 5 >= 0) { cost = min(cost, f[i - 5] + 1); }
        if (i - 11 >= 0) { cost = min(cost, f[i - 11] + 1); }
        f[i] = cost;
        cout << "f[" << i << "]=" << f[i] << endl;
    }

}

  • 题目二

  • 最长上升子序列（LIS）问题：给定长度为n的序列a，从a中抽取出一个子序列，这个子序列需要单调递增。问最长的上升子序列（LIS）的长度。
    e.g. 1,5,3,4,6,9,7,8的LIS为1,3,4,6,7,8，长度为6。

  • 题解

  • 1.从小试大

  • 我们这里先用前几个数观察 f(1)=1 f(2)=2 f(3)=2 f(4)=3 即f(4)=f(3)+1;f(3)=f(1)+1; 即前面最大的+1

  • f(n)=max(f(前面))+1;

  • 这里使用双循环 

  • 代码

     

  • #include<iostream>
#include<string>
using namespace std;
int main() {
    int a[8] = {1,5,3,4,6,9,7,8};
    int b[8] = {1};
    for (int i = 0; i < 8; i++)
    {
        for (int j = 0; j < i; j++)
        {
            if(a[j]<a[i]){
                b[i] = max(b[i], b[j] + 1);
            }
        }
        cout << "b["<<i<<"]=" << b[i]<<endl;
    }
    cout << b[7] << endl;

}

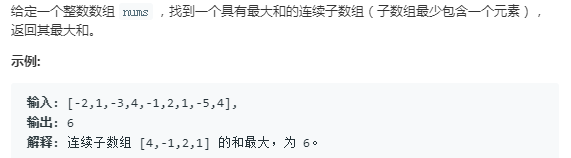
  • 题目三

  • 题解

  • 找到前面的最大的然后加上本身的数 和本身的数进行比较即可

  • lent[0] = nums[0];

  • lent[i] = max(lent[i - 1]+nums[i], nums[i]);

  • 代码

  • #include<iostream>
#include<string>
using namespace std;


int main() {
    int nums[9] = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
    int lent[9];
    int max1 = 0;
    lent[0] = nums[0];
    for (int i = 1; i < 9; i++) {
        lent[i] = max(lent[i - 1]+nums[i], nums[i]);
        cout << "lent[" << i << "]=" << lent[i] << endl;
        if (lent[i] > max1) {
            max1 = lent[i];
        }
    }
    cout << max1 << endl;
}

  • 题目四

  • 题解

  • 这题考虑到不能相邻 所以 上一个房间与本房间挨着所以只需要上个房间的最大值 但 上上一个房间不挨着本房间所以可以加上本房间的金额即

  • b[i] = max(b[i-1], b[i-2] + a[i]);

  • 代码

  • #include<iostream>
#include<string>
using namespace std;
int main() {
    int a[5] = {1,25,10,22,55};
    int b[5];
    for (int i = 0; i < 5; i++) {
        if (i==0) {
            b[i] = a[i];
        }
        else if(i==1)
        {
            b[i] = max(a[0], a[1]);
        }
        else if (i > 1) {
            b[i] = max(b[i-1], b[i-2] + a[i]);
        }
        cout << b[i] << endl;
    }
}

  • 题目五

  • 题解

  • 找几个前面的例子一试 发现了 当N为偶数 爱丽丝就会赢 所以这题就做完了(不是)

  • 既然是动态规划 我们就来看一下这题怎么做

  • 以30为例 30能赢 那么他的因数中有能赢的 那么这个因数既然能赢 那么这个因数的因数也有可以胜利的

  • 就是这样我们推到2就会发现 2的倍数就是赢

  • 代码

  • #include<iostream>
#include<string>
using namespace std;


int main() {
     bool dp[31]; 
    dp[1] = false;
    for (int i = 2; i <= 30; i++) 
    {
        dp[i] = false;
        for (int j = 1; j < i; j++)
        {
            if (i % j == 0 && dp[i - j] == false) 
            {
                dp[i] = true;
                break;
            }
        }
    }
    cout << dp[30] << endl;
}

  • 心得

    动态规划是一种特殊的思想 可以剩下很多内存并且减少时间复杂度 但是不容易想到 需要多加练习

  • 说实话我在写题解的时候并不知道该怎么写 因为很多东西脑子里有但是不知道怎么表达 只能写一些重点上去了(反正也是我一个人看)

posted @ 2022-03-26 15:11  无聊的阿库娅  阅读(60)  评论(0)    收藏  举报