第三章 梯度下降

梯度下降就是猜测一个初始的点，然后向值变小的方向去走

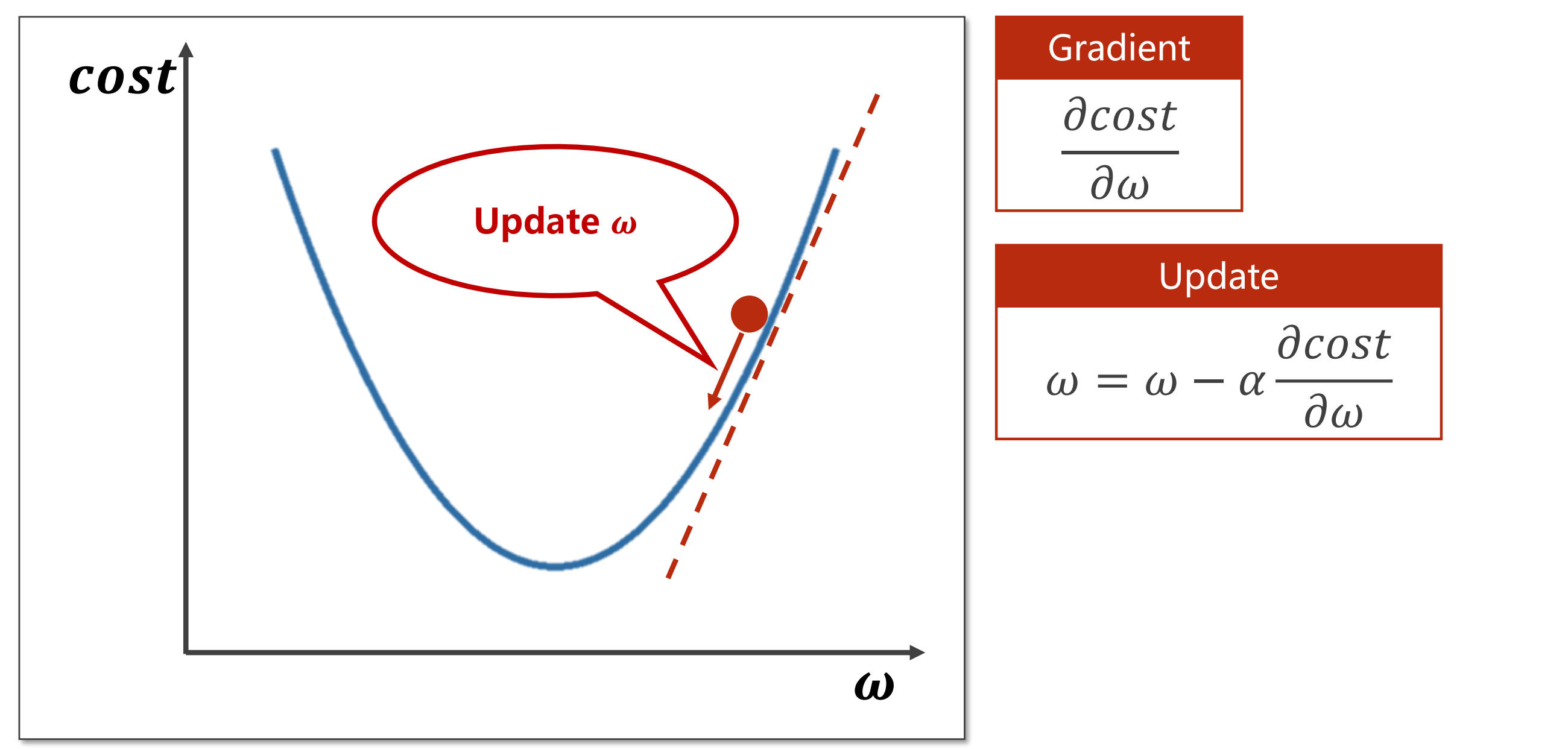
这个梯度实际就是导数，我们需要找到极值点，也就是导数为0的点。初始我们猜测了一个初始值后，我们需要判断这个点接下来是向左还是向右，根据梯度\(\frac{\partial cost}{\partial \omega}\)且我们需要找到一个最小的权重\(\omega\)可知，我们需要向导数的负方向走才会使值减小，所以梯度的更新策略是\(\omega = \omega - \alpha\frac{\partial cost}{\partial \omega}\)。我们梯度的定义实际就是我们的成长函数对权重进行求导数，这样我们就可以得到它的上升方向。之所以是上升方向是通过导数定义$\displaystyle \lim_{x \rightarrow \infty} \frac{f(x + \Delta x)-f(x)}{\Delta x} $可知，x加上一个数值之后他的函数值变大，说明这肯定是一个增函数，说明在数值的正方向它在上升，那我们就需要向它的反方向走。所以是减去。
梯度下降法找到的是局部最优点，但因为深度学习中局部最优点很少，这个并不是困扰，真正困扰的是鞍点，即斜率为0的点。可以加一个动量解决鞍点。即动量梯度法。
通过求导我们可以得到如下公式：

接下来开始代码：

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0 # 猜测一个初始权重

def forward(x): # 定义线性模型
    return x * w

def cost(xs, ys): # 定义损失函数MSE
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

def gradient(xs, ys): # 定义梯度函数
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y) # 求导的导数公式
    return grad / len(xs)

print('predict (before training)', 4, forward(4))
for epoch in range(100): # 进行梯度更新
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= 0.01 * grad_val
    print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('predict (after training)', 4, forward(4))

plt.plot([x for x in range(1,101)],loss_list)
plt.ylabel("Loss")
plt.xlabel("epoch")
plt.show()

随机梯度下降

提供N个数据，但是随机的从里面选一个，更新的公式就变成了拿单个样本的损失来对权重进行求导，然后更新。

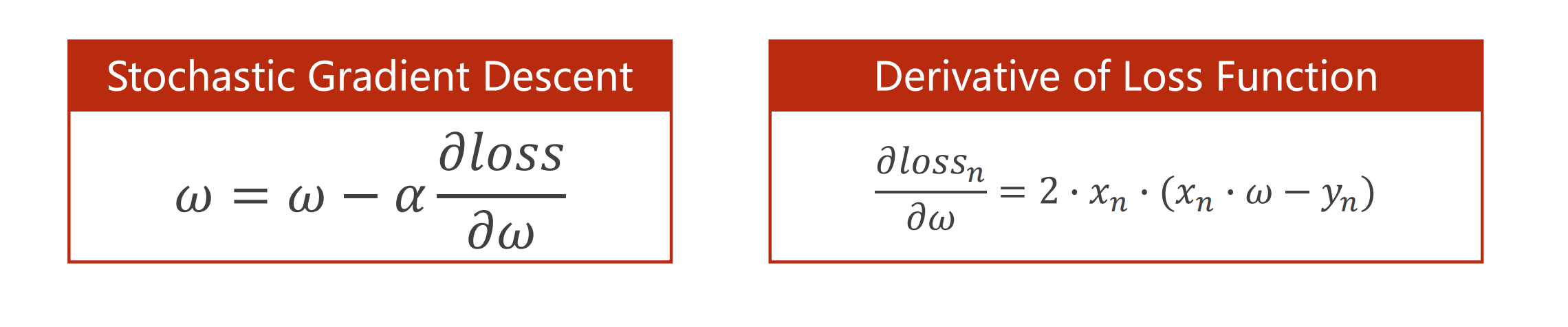
使用随机梯度下降原因

损失函数可能有鞍点，到达鞍点就没办法继续往前走。
随机梯度下降是引入了噪声所以有机会走出去，有时间查阅补充具体的。

对比

梯度下降可以进行并行计算，性能低一点但是时间复杂度低
随机梯度下降不能并行计算，新能高但是时间复杂度也高
所以在深度学习中一般会进行折中而使用批量的梯度随机下降。