数论

BSGS

用来求解离散对数问题，即求解满足给定 \(a,b,p\)，\(a^n \equiv b \pmod{p}\) 的 \(n\) 的最小正整数解。

算法流程

我们可以将该问题分成两类：

普通BSGS

即满足 \(a\perp p\) 的情况。

发现在这种情况下，\(a\) 有逆，而 BSGS 根据这个性质，设计了一个根号的算法。

因为此时 \(a^n\) 的循环节长度为 \(\varphi(p)\)，所以我们知道 \(0\le n< \varphi(p)\)（欧拉定理），于是我们设 \(s=\sqrt{\varphi(p)}\)，那么 \(n\) 就可以表示为 \(n=k\times s+c\)，\(0\le c <s\)。

看到这个东西类似于光速幂，沿用这个思路，我们可以先处理出所有 \(a^c\)，然后再枚举 \(k\)，但是发现我们需要找到最小的 \(c\)，使得 \(a^c=b\times \frac{1}{a^{k\times s}}\)，发现可以选择用哈希表，然后就是 \(\mathcal O(\sqrt p)\) 的。

发现这个东西还需要求 \(\frac{1}{a^{k\times s}}\)，可能会带一个 \(\log\)，比较不好。但是我们可以把 \(n\) 重新表示成 \(k\times s-c\)，然后就是求 \(b\times a^c=a^{k\times s}\)。发现可以将 \(b\times a^c\) 打包放进哈希表，求最大的 \(c\) 就行了。

exBSGS

什么都有拓展，顾名思义，就是不保证 \(a\perp p\)，\(a\) 就没有逆。

根据同余式的性质，我们可以将 \(a,b,p\) 除掉 \(\gcd(a,p)\)，注意，\(a\) 有若干次方，所以除一次可能不够，要把 \(a\) 除到与模数互质才行，所以就变成了 \(a^{c+x}，c 为常数\)，那么 \(a^1\sim a^x\) 就需要特殊处理一下。中间除的时候发现 \(\gcd(a,p) \nmid b\) 的话判断一下无解就好了。

运用场景

\(a\) 是整数

大部分情况下就是用来解离散对数问题。

\(a\) 是矩阵

注意到，\(a\) 不一定要是整数。他还可以是矩阵等其他东西。

但是使用矩阵的时候要注意一定要有逆矩阵，听说可以用行列式判断矩阵有没有逆，但是高维之后就显得有些不适用了。大部分情况还是要根据题目条件自行分析判断。

所以说递推一些数列，或者是一些奇怪的操作时也可以运用 BSGS 的思想。

Miller_Rabin

本质

运用了费马素数测试和二次探测定理。

顾名思义，就是先用用费马小定理来检测素数。具体的，设当前检测的素数为 \(p\)，如果 \(\exist a,a^{p-1}\not\equiv 1 \pmod{p}\)，那么 \(p\) 一定不是素数。

但是这样检测并不能覆盖所有素数，所以我们再打了一个补丁，用二次探测定理来补上这个漏洞。

而二次探测定理即为：若 \(p\) 是质数，那么 \(x^2\equiv 1\pmod{p}\) 只有 \(x=1\) 和 \(x=p-1\) 这两个解。

然后我们就可以运用这两个方法判断质数。注意到费马检测的 \(a\) 并不固定，但是前 \(12\) 个质数作为 \(a\) 可以成功检测出所有 \(p\le 10^{18}\) 的质数。

不难发现时间复杂度为 \(\mathcal O(T\times \log^2 n)\) 的，\(T\) 为检测次数。

代码

贴个模板

运用

判断素数。Pollard_rho 也要用到。

Pollard_rho

如何分解 \(n\le 10^{18}\) 的质因数？

用 Pollard_rho。

二次剩余

是啥来着。

斐波那契循环节

通项公式是啥？

狄克卷积

狄利克雷卷积，在数论中是一个比较好用的辅助工具。

基础知识

定义

设 \(h=f*g\)，其中 \(*\) 为狄利克雷卷积符号。则：

\[h(i)=\sum_{d\mid i} f(d)\times g(\frac{i}{d}) \]

多个函数卷积可以表示为：

若

\[h=f_1*f_2*f_3...f_{k-1}*f_k \]

那么

\[h(n)=\sum_{d_1\times d_2\times d_3...d_{k-1}\times d_k=n}f_1(d_1)\times f_2(d_2)\times f_3(d_3)...\times f_{k-1}(d_{k-1})\times f_k(d_k) \]

狄利克雷卷积中的单位元为 \(\varepsilon(n)=[n=1]\)，即 \(f*\varepsilon=f\)。

以及只要 \(f(1)\not=0\)，那么存在 \(g*f=\varepsilon\)，称 \(g\) 为 \(f\) 的逆元，可以表示为 \(f^{-1}\)。

而特别地，\(1(n)=1\) 的逆元是 \(\mu\)，即 \(1*\mu=\varepsilon\)，这个就是莫比乌斯反演，后面会讲。

一些性质

由定义易得狄利克雷卷积满足交换律，结合律，分配律。

\(\color{Red}{积性函数和积性函数的狄利克雷卷积是积性函数}\)。

这一点十分重要，在后面的许多题目/筛法中都会用到。特别是 PN 筛，考试时因为忘记这一点导致复杂度过高了。

计算方式

显然，可以暴力枚举约数 \(\mathcal O(n\times \sqrt{n})\)，但是明显可以 \(\mathcal O(n\times \log n)\)。

同时，我们同样可以 \(\mathcal O(n\times \log n)\) 已知 \(f,g\)，求 \(h=f/g=f*g^{-1}\)。

具体的，我们可以将上式移项得到 \(h*g=f\)，展开得到：

\[f(i)=\sum_{d\mid i} h(d)\times g(\frac{i}{d}) \]

而我们把 \(i=1\) 带入，得到 \(h(1)=\frac{f(1)}{g(1)}\)。

而同理，对于 \(i\ge 2\) 的那些 \(h(i)\)，我们考虑递推的过程，当前已经算好了 \(h(1)\sim h(i-1)\)，于是我们将 \(d=i\) 单独提出来，可以得到：

\[f(i)=h(i)\times g(1)+\sum_{d\mid i,d<i} h(d)\times g(\frac{i}{d}) \]

因为 \(\sum\) 里面的东西都已经算好，所以将其移项过后就可以得到当前 \(h(i)\)。

拓展

狄利克雷前/后缀和

狄利克雷前缀和表示为 \(h(n)=\sum_{d\mid n} f(d)\)，即对所有约数求和，同时也可以表示为 \(h=f*1\)，而此时，我们可以用高维前缀和将其优化为 \(\mathcal O(n\times \log\log n)\)。

而后缀和即对倍数求和，同样可以用高维后缀和达到同样的效果。

莫比乌斯反演

莫比乌斯函数

\(\mu\) 是一个性质十分好的函数，看起来就很像容斥系数，但实际上我们也可以把他当做容斥系数。

\[\mu(n) = \begin{cases} 1 & \text{$n=1$} \\ (-1)^k & \text{$n=p_1\times p_2...\times p_k$}\\ 0& \text{otherwise} \end{cases} \]

反演

而之前提到过 \(1*\mu=\varepsilon\)，如何证明？

设当前 \(n=p_1^{r_1}\times p_2^{r_2}...\times p_k^{r_k}\)。

那么因为 \(\mu\) 在 \(r_i>1\) 时没有贡献，所以设 \(n'=p_1\times p_2...\times p_k\)

\[\sum_{d\mid n} \mu(d)=\sum_{d\mid n'} \mu(d)=\sum_{i=0}^{k}(-1)^i\times C_{k}^{i}=(-1+1)^k \]

而 \(k=0\)，即 \(n=1\) 时，上式为 \(1\)，其他情况均为 \(0\)，故得证。

使用方式

我们知道 \(\mu *1=\varepsilon\)，所以最常见/好用的形式就是把 \([...=1]\) 给模范掉。

比如 \([\gcd(a,b)=1]\)，我们就可以用莫比乌斯反演掉，变成 \(\sum_{d\mid \gcd(a,b)}\mu(d)=\sum_{d\mid a,d\mid b}\mu(d)\)，这个时候，一般都会改成枚举 \(d\)，然后一顿操作。

比如求

\[\sum_{i=1}^{n}\sum_{j=1}^{m} [\gcd(i,j)=k] \]

首先，我们发现 \(=k\) 很烦，考虑到若 \(\gcd(i,j)=k\)，那么 \(i,j\) 一定是 \(k\) 的倍数，于是可以把 \(k\) 提出来。

\[\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor} [\gcd(i\times k,j\times k)=k]=\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor} [\gcd(i,j)=1] \]

然后发现变成了模范模板

\[\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor} [\gcd(i,j)=1]=\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor}\sum_{d\mid i,d \mid j} \mu(d) \]

然后交换求和顺序

\[\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor}\sum_{d\mid i,d \mid j} \mu(d)=\sum_{d=1}^{n} \mu(d) \lfloor \frac{n}{k\times d}\rfloor \lfloor \frac{m}{k\times d}\rfloor \]

然后发现可以整除分块，但是有两个数？直接一起！

int r=1;
for(int i=1;i<=min(x,y);i=r+1){
  r=min(x/(x/i),y/(y/i));
}

上文说的都是比较基础的莫比乌斯反演题，还有一些比较综合的例题，需要用到容斥等高级的思想。容易注意到的是莫比乌斯函数本身就是类似容斥的系数，特别是有关质因数的容斥，\((-1)^k\) 看起来就特别熟悉。

有一个经典的例题：

求 \(1\sim n\) 内不存在 \(d>1,d^2 \nmid x\) 的 \(x\) 的个数。

我们假设满足条件的 \(d\) 的最大值为 \(dmax\)，那么上式显然可以被改写为：

\[\sum_{i=1}^{n}[dmax_i=1]=\sum_{i=1}^{n}\sum_{d\mid dmax_i}\mu(d)=\sum_{i=1}^{n}\sum_{d^2\mid i}\mu(d) \]

而交换求和顺序可以得到

\[\sum_{i=1}^{n}\sum_{d^2\mid i}\mu(d)=\sum_{d=1}^{\sqrt{n}} \mu(d) \times \lfloor \frac{n}{d^2} \rfloor \]

然后就整除分块一下就行了。注意到，其本质就是在做容斥。

亚线性筛

杜教筛

思路

思路比较简单，但是一般用来筛算一些常见的积性函数的前缀和。

假设我们要筛 \(s(n)=\sum_{i=1}^{n}f(i)\)，其中 \(f\) 为积性函数。

其核心的思想就是构造 \(h=f*g\)，使得 \(g,h\) 都比较好算。

设 \(s(i)=\sum_{i=1}^{n}f(i)\)，我们尝试表示一下刚才的思路：

\[\sum_{i=1}^{n} h(i)=\sum_{i=1}^{n}\sum_{d\mid i}f(d)\times g(\frac{i}{d})=\sum_{i=1}^{n}\sum_{d\mid i}f(\frac{i}{d})\times g(d) \]

然后交换一下求和顺序：

\[=\sum_{d=1}^{n}g(d)\sum_{i=1}^{\lfloor\frac{n}{d} \rfloor}f(i)=\sum_{d=1}^{n}g(d)\times s(\lfloor\frac{n}{d} \rfloor) \]

然后我们发现式子里神奇的出现了 \(s\)，于是考虑把 \(d=1\) 单独提出来，再移项，就可以得到：

\[\sum_{i=1}^{n}h(i)=g(1)\times s(n)+\sum_{d=2}^{n}g(d)\times s(\lfloor\frac{n}{d} \rfloor) \]

\[g(1)\times s(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\times s(\lfloor\frac{n}{d} \rfloor) \]

然后我们发现这个东西就可以递归计算了！

例子

举两个例子，求：

\[s_1(n)=\sum_{i=1}^{n}\mu(i),s2(n)=\sum_{i=1}^{n}\varphi(i)。 \]

先考虑 \(\mu\) 怎么求，根据杜教筛的思想，我们可以构造一个 \(h=\mu*g\)，根据莫比乌斯反演，不难想到可以构造 \(g(n)=1\)，这样 \(h(n)=[n=1]\)，十分的方便。

然后套用上文的公式可以得到：

\[s_1(n)=1-\sum_{d=2}^n s_1(\lfloor\frac{n}{d} \rfloor) \]

然后就比较好计算了。

知道 \(\mu\) 怎么求后，\(\varphi\) 也自然是一样的，同样的，根据欧拉反演，我们仍然构造 \(g(n)=1\)。那么 \(h(n)=n\)，同样也比较好算：

\[s_2(n)=\frac{n\times (n+1)}{2}-\sum_{d=2}^n s_1(\lfloor\frac{n}{d} \rfloor) \]

这两个比较基础，下面看一个稍微难一点的：

求

\[s_3(n)=\sum_{i=1}^{n} d(i) \]

\(d(i)\) 表示 \(i\) 的约数个数。

怎么构造？

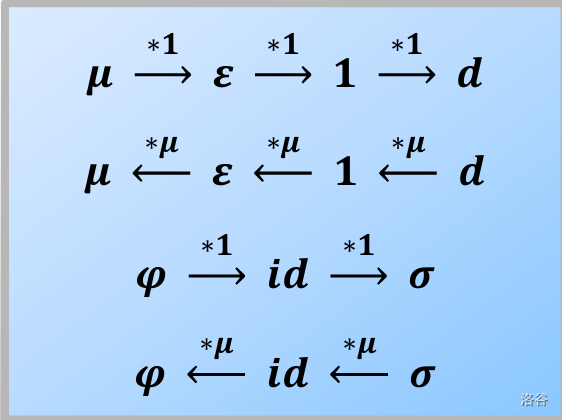
哦，构造 \(g=\mu\) 就行了！

\[\mu(1)\times s_3(n)=n-\sum_{d=2}^{n}\mu(d)\times s_3(\lfloor\frac{n}{d} \rfloor) \]

要算 \(\mu\)？同样用杜教筛即可，注意到用到的 \(\mu\) 都是 \(n\) 的整除分块集合内的数，所以相当于就是筛了一遍 \(s_1(n)\)。

进阶例子

那如果求：

\[s_4(n)=\sum_{i=1}^{n} i^k\times \mu(i),s_5(n)=\sum_{i=1}^{n} i^k\times \varphi(i) \]

发现不好直接卷一些东西进去，但是这两个求和其实十分套路，根据欧拉反演和莫比乌斯反演可以知道两者对于约数的函数值求和之后都十分好算。而狄利克雷卷积本身就有约数的形式，于是不难想到把 \(i^k\) 提出来就可以反演了。

那答案就呼之欲出了，卷一个 \(id^k\)！

\[\sum_{i=1}^{n}h_4(n)=\sum_{i=1}^{n}\sum_{d\mid i}d^k\times \mu(d)\times (\frac{i}{d})^k= \sum_{i=1}^{n}i^k\sum_{d\mid i}\mu(d) \]

然后发现这是莫比乌斯反演：

\[\sum_{i=1}^{n}h_4(n)=\sum_{i=1}^{n}i^k \]

发现是幂和的形式，比较好求，于是就有：

\[s_4(n)=\sum_{i=1}^{n}i^k-\sum_{d=2}^{n}d^k\times s_4(\lfloor\frac{n}{d} \rfloor) \]

\(s_5\) 同样也卷一个 \(id^k\)，前面的推导过程类似，只不过变成了欧拉反演：

\[\sum_{i=1}^{n}h_5(n)=\sum_{i=1}^{n}i^k\sum_{d\mid i}\varphi(d)=\sum_{i=1}^{n}i^k\times i=\sum_{i=1}^{n}i^{k+1} \]

\[s_5(n)=\sum_{i=1}^{n}i^{k+1}-\sum_{d=2}^{n}d^k\times s_5(\lfloor\frac{n}{d} \rfloor) \]

时间复杂度

接下来就是一个比较重要的东西了：复杂度是多少？递归的复杂度不是很好分析，所以考虑记忆化之后的复杂度：

\[T(n)=\sum_{i=1}^{\sqrt{n}}O(\sqrt{n})+\sum_{i=1}^{\sqrt{n}}O(\sqrt{\frac{n}{i}}) \]

然后就需要用到积分，不是很会积分，所以直接说结论：\(T(n)=O(n^{\frac{3}{4}})\)。

然后我们又会发现，实际上我们可以预处理一部分的 \(s_i\)，考虑设定一个阈值 \(T\)，\(\mathcal O(T)\) 处理出 \(1\sim T\) 的 \(s\)。大于 \(T\) 的部分再递归，然后就变成了：

\[\sum_{i=1}^{\lfloor\frac{n}{T}\rfloor}O(\sqrt{\frac{n}{i}})=O(\frac{n}{\sqrt T}) \]

然后两部分加起来就是 \(\mathcal O(T+\frac{n}{\sqrt T})\) 的，取 \(T=n^{\frac{2}{3}}\) 时复杂度为 \(\mathcal O(n^{\frac{2}{3}})\)。当然，推导也要用到积分。

总结

核心在于构造 \(h=f*g\)，使得 \(h,g\) 好求，一些经典的例子在上面的图片里。还有就是卷 \(id^k\) 的技巧。

PN 筛

Powerful Number!

同样用来筛积性函数前缀和，但是有一定局限性，并且只能单次调用。

思路

该筛法基于一个事实：

定义 Powerful Number（幂数） 为形如 \(x=p_1^{r_1}\times p_2^{r_2}\times p_3^{r_3}...\times p_{k-1}^{r_{k-1}}\times p_{k}^{r_{k}}\)，且 \(r_i\ge 2\) 的数。那么 \(n\) 以内的 Powerful Number 数量为 \(\mathcal O(\sqrt n)\) 级别的。

下面给出证明：

易得，任何 \(x\) 均能被表示为 \(x=a^2\times b^3\)。考虑计数，\(cnt=\sum_{a=1}^{\sqrt{n}} \lfloor ^3\sqrt {\frac{n}{a^2}}\rfloor\)，然后积一下分就能得到 \(cnt=O(\sqrt n)\)。

根据幂数的数量，幂数筛尝试构造一个函数 \(h\)，使得其仅在幂数处有取值，即在非幂数处都为 \(0\)。容易发现这就等价于 \(h(p)=0,p\in \text{Prime}\)。

如何让 \(h\) 与 \(f\) 有关系，同时又能满足上述条件呢？接下来就十分妙了！

尝试构造函数 \(g\)，使得 \(g(p)=f(p),p\in \text{Prime}\)，且 \(g\) 为积性函数。

令 \(f=g*h\)，神奇的事情发生了！考虑质数处的取值：

\[f(p)=g(1)\times h(p)+g(p)\times h(1) \]

因为 \(g\) 为积性函数，所以 \(g(1)=1\)，同时，前面着重提到过，\(h=f*g^{-1}\) 也是积性函数。所以 \(h(1)=1\)，那么带回去，惊人的发现：

\[f(p)=1\times h(p)+g(p)\times 1\rightarrow h(p)=0 \]

上述条件都满足了！！！

然后我们推一下式子：

\[\sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}\sum_{d\mid i}h(d)\times g(\frac{i}{d})=\sum_{d=1}^{n}h(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor} g(i) \]

不难发现，我们实际上只需要算 \(\mathcal O(\sqrt n)\) 个位置的取值，并且需要用到 \(g\) 的前缀和。

考虑如何知道 \(1\sim n\) 内所有的幂数。

直接根据 \(p_i^{r_i}\) 爆搜就行了，但是不能有继承的状态，也就是说搜索时每一次 \(x\) 都要变大。不然中间连续的一段无效 \(\times 1\) 会让复杂度爆炸。

然后就是计算 \(h\)，既然爆搜都已经是枚举了 \(p_i^{r_i}\)。我们可以花 \(\mathcal O(\sqrt n\times \log n)\) 的时间复杂度计算出所有 \(h(p^k)\)，然后乘起来。算 \(h(p^k)\) 就用前文提到的递推来求就行了。

但是如果 \(g\) 不是简单的积性函数，那么可能复杂度瓶颈就在算 \(g\) 的前缀和处。

但如果 \(g\) 的前缀和可以 \(O(1)\) 算，那么 PN 筛的速度优势就比较明显了。

例子

经典例题

首先做一些简单的推导，发现题目求的是：

设 \(x=p_i^{r_i},r_i>0\)，\(s(x)=p_i^{r_i-1}\)。

\[\sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}\frac{i}{d(\frac{i}{s(i)})}=\sum_{i=1}^{n}\frac{i}{\prod_{\prod p_j^{ r_j}=i} r_j} \]

我们神奇的发现这个函数是一个积性函数。并且 \(f(p)=p\)。于是，不难想到使用 PN 筛，\(g\) 显然等于 \(id\)。

然后写出式子：

\[\sum_{i=1}^{n}f(i)=\sum_{d=1}^{n}h(d)\times \frac{\lfloor\frac{n}{d}\rfloor\times (\lfloor\frac{n}{d}\rfloor+1)}{2} \]

然后发现这个式子异常简洁，并且也达到了 PN 筛的理论最优复杂度！

总结

只要找到积性函数 \(g\) 使得 \(g(p)=f(p)\)，那么就可以用 PN 筛。然后预处理 \(h(p^k)\)，搜索时乘起来得到 \(h(x)\)。（不过一般来说只有 \(g\) 比较简单的时候才好做）

Min_25 筛

好东西，基本上所有积性函数都可以筛。

筛质数点取值

先考虑 \(f(p)=1\) 怎么做。也就是筛质数个数。

考虑埃筛的过程，设 \(G(n,i)\) 表示 \(1\sim n\) 中经过第 \(i\) 轮埃筛后剩下的个数。

发现这个东西有一点像 dp，考虑从 \(G(n,i-1)\) 转移过来，那么减去的个数就是第 \(i\) 轮被筛掉的个数。\(\lfloor \frac{n}{prime_i} \rfloor\) 显然会算重，因为我们要保证 \(prime_i\) 是最小的质因子。

不难想到考虑可以改为把 \(\lfloor\frac{n}{prime_i} \rfloor\) 中最小质因子 \(\ge prime_i\) 的个数计算出来。

神奇的事情发生了！这就是一个子问题，他的值是 \(G(\lfloor\frac{n}{prime_i} \rfloor,i-1)\)，但是这里面还包含 \(prime_1\sim prime_{i-1}\)，减掉就行了。

于是得到了以下式子：

\[G(n,i)=G(n,i-1)-[G(\lfloor\frac{n}{prime_i} \rfloor,i-1)-(i-1)] \]

发现这个式子可以递推，然后就是分析复杂度。

因为我们只需要枚举 \(\sqrt n\) 以内的质数，所以总的时间复杂度就是：

\[T(n)=\sum_{i=1}^{\sqrt{n}} O(\frac{\sqrt{i}}{\log \sqrt{i}})+\sum_{i=1}^{\sqrt{n}} O(\frac{\sqrt{\frac{n}{i}}}{\log \sqrt{\frac{n}{i}}}) \]

然后放缩加积分出来大约为：\(O(\frac{n^{\frac{3}{4}}}{{\log n}})\)。

直接实现的常数比较大，所以我们可以开数组滚动计算，发现 \(\lfloor\frac{n}{prime_i} \rfloor\) 只有 \(\mathcal O(\sqrt{n})\) 种取值，所以可以记录两个数组来映射编号。

还有一些常数优化的细节，代码如下：

for(int i=1;i<=cnt;i++){
		while(now>0&&b[now]<prime[i]*prime[i]){
			now--;
		}
		for(int j=1;j<=now;j++){
			int noww=b[j]/prime[i];
			g[j]-=(noww>=prime[i-1])?((g[noww<=len?id1[noww]:id2[n/noww]])-(i-1)):0;
		}
	}

筛所有数的前缀和

注意，不一定是一些常见的函数，如果函数计算可以转换为与质因子指数相关的式子，同样可以计算。

设 \(S(n,i)\) 表示 \(2\sim n\) 中最小质因子 \(> prime_i\) 的值之和。

考虑如何计算。

不难想到枚举最小质因子进行计算，即：

\[S(n,i)=\sum_{x=i+1}^{cnt}\sum_{j=1}^{prime_x^j\le n}f(prime_x^j)\times S(\lfloor \frac{n}{prime_x^j}\rfloor,x) \]

如果求的是 \(\sum_{i=1}^{n} d(i)\)，就是：

\[S(n,i)=\sum_{x=i+1}^{cnt}\sum_{j=1}^{prime_x^j\le n}(j+1)\times (S(\lfloor \frac{n}{prime_x^j}\rfloor,x)+[j\neq 1]) \]

但是实际测试会发现这个东西跑得特别的慢，因为我们重新算了所有 \(prime_i\sim n\) 中质数点的取值。而根据之前筛质数个数的部分，我们发现质数点实际上是比较好算的，只需要前缀和相减一下，于是我们就只需要枚举 \(\sqrt n\) 以内的质数了。

\[S(n,i)=G(n)-G(prime_i)+\sum_{x=i+1}^{x\le cnt,prime_x^2\le n}\sum_{j=1}^{prime_x^j\le n}(j+1)\times (S(\lfloor \frac{n}{prime_x^j}\rfloor,x)+1) \]

然后时间复杂度就变为 \(O(\frac{n^{\frac{3}{4}}}{{\log n}})\) 了，但是日常使用会发现直接写递归在 \(10^9\sim 10^{12}\) 范围内都跑的很快，所以并不需要记忆化。

update on 2025.6.21

考了 min_25，发现之前并没有写筛所有点值的和，于是补充了一下，现在会了。