COMSOL 基础学习笔记

相关资料

官网 $ $ 博客

工作流程

1. 定义需要求解的问题类型
2. 绘制（或导入）CAD 模型
3. 定义每个求解域的材料属性
4. 设定荷载和边界条件
5. 网格剖分
6. 求解模型
7. 后处理和报告结果
8. 修改和优化

几何

二维

基本对象：

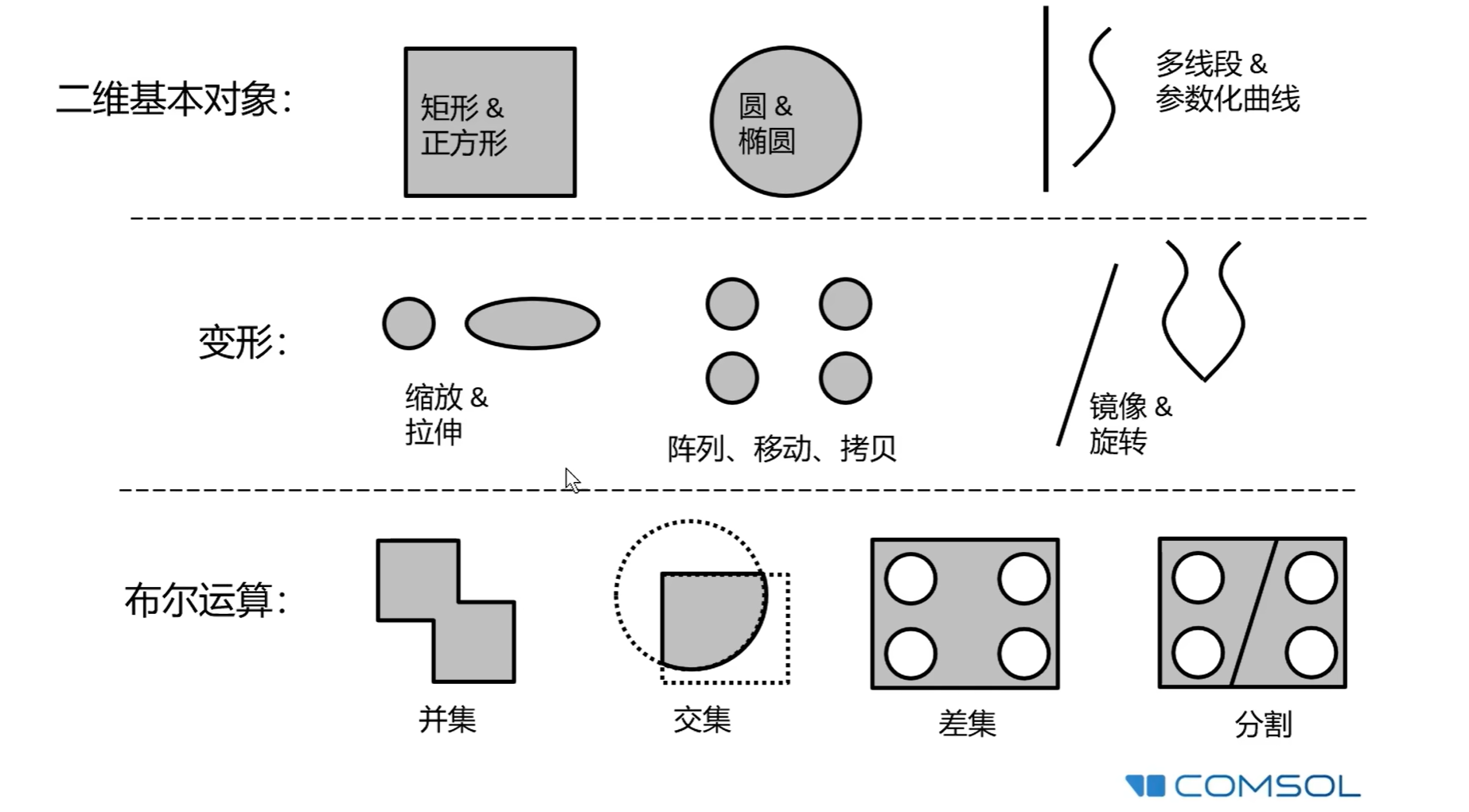
例：粗糙面的画法（参数化）

step1：定义随机函数

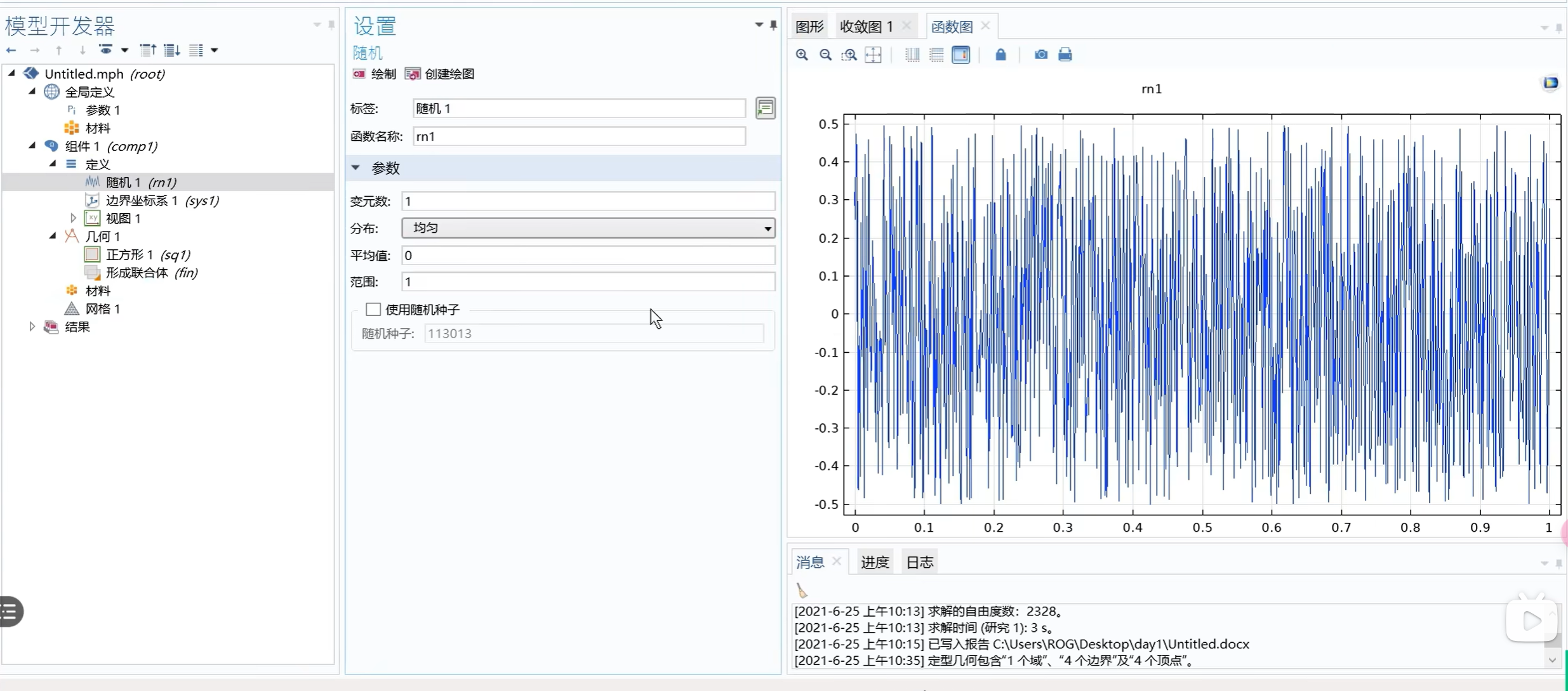
step2：设置参数化曲线：

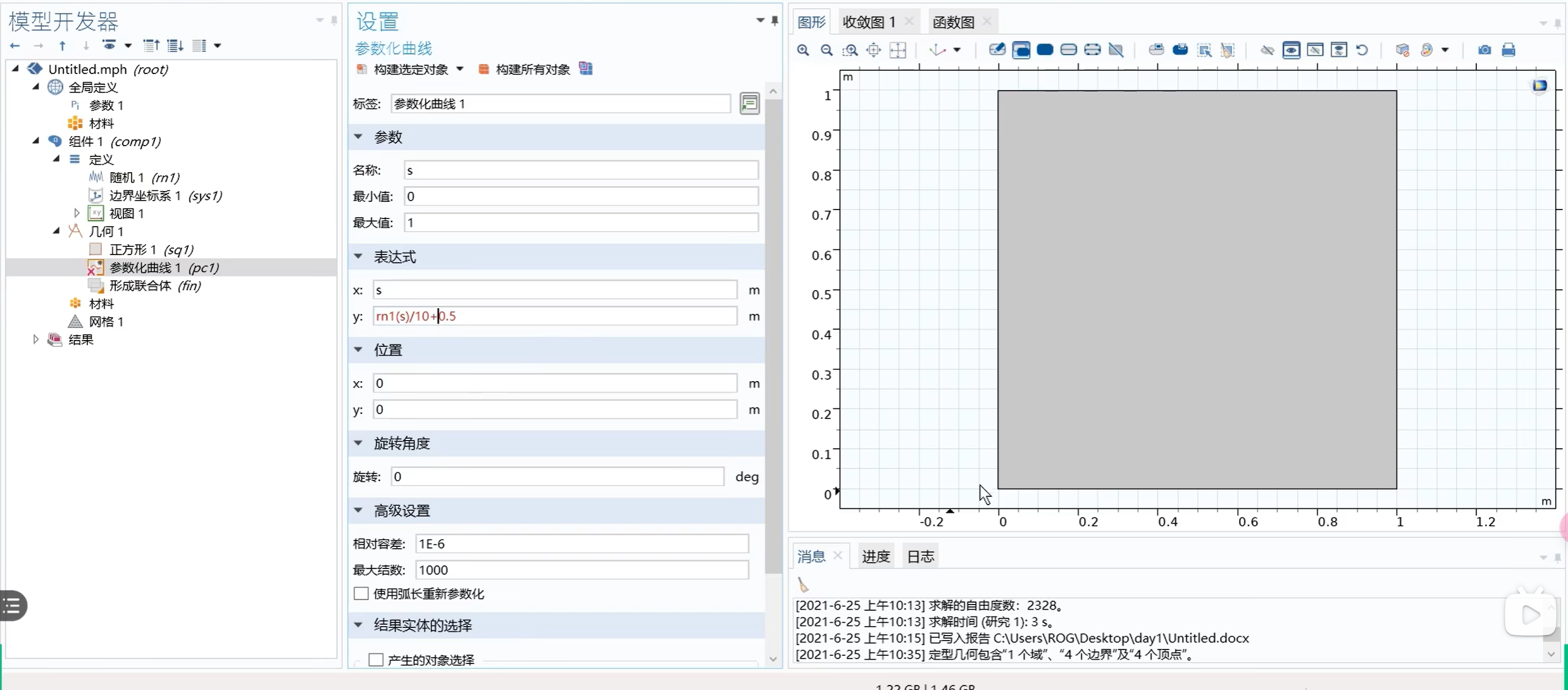
三维

基本对象

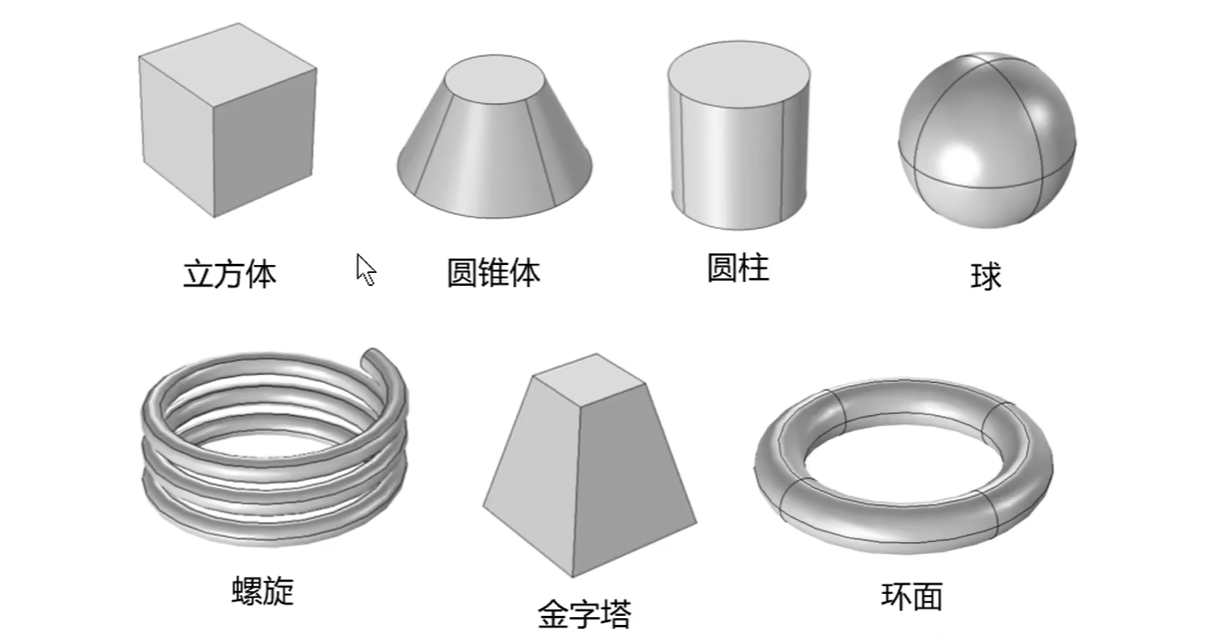
二维变换到三维

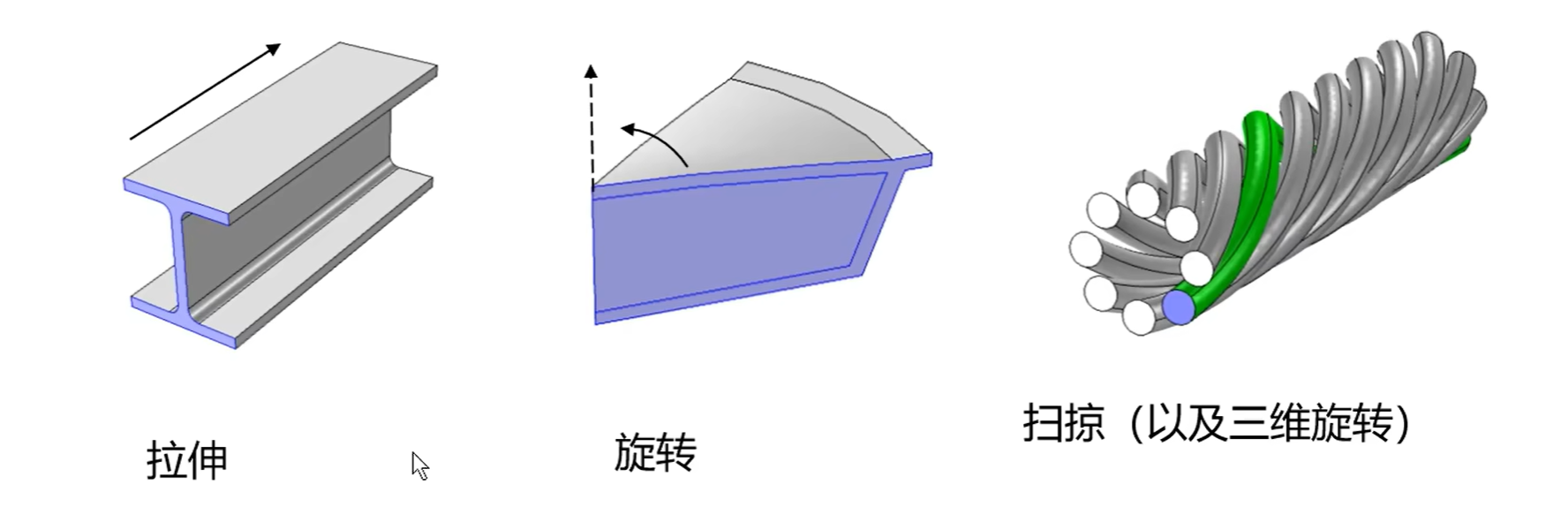
具体实现方法：（以拉伸为例）

先新建工作平面，把需要拉伸的几何体放在工作平面上。然后对工作平面进行拉伸：

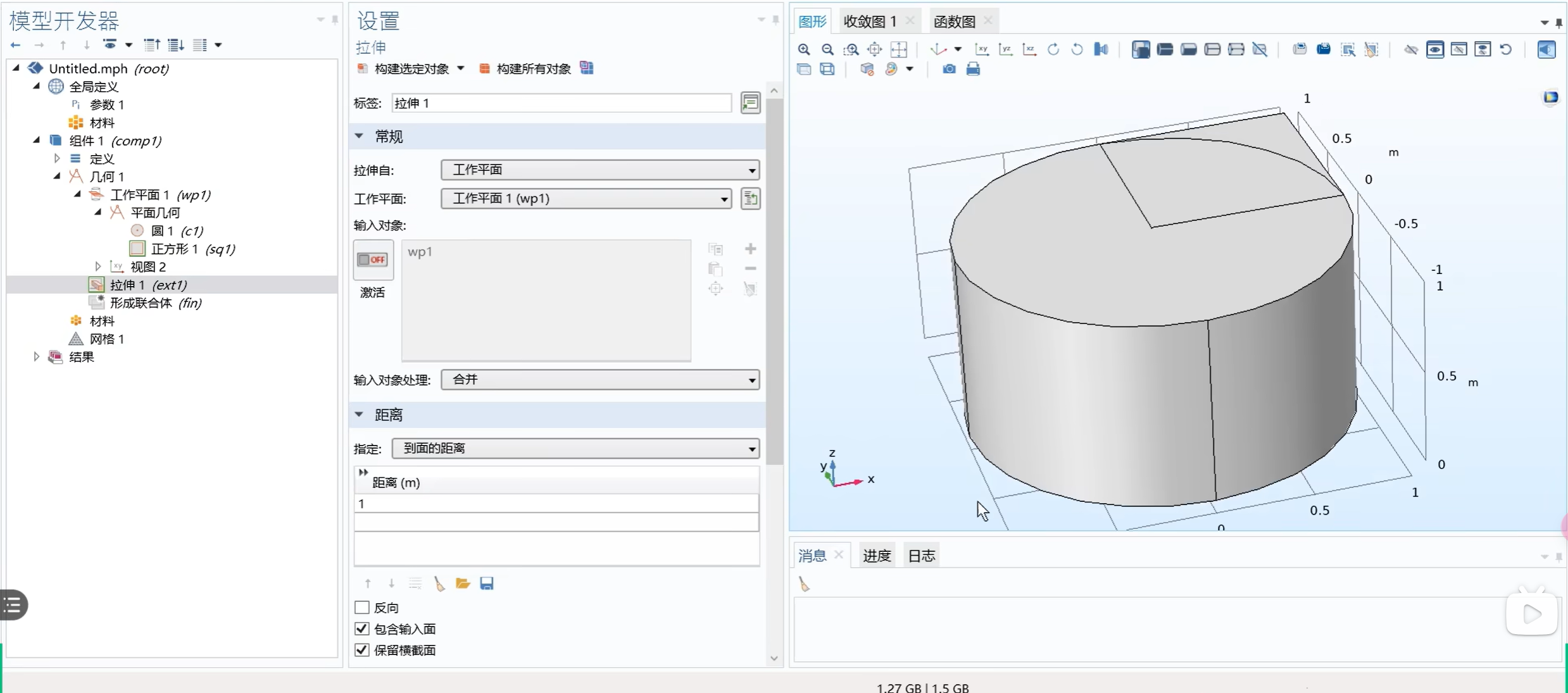
三维变换到二维（截面）

画好几何体 - 新建工作平面（就是即将截出的截面） - 新建二维组件，找到几何，选择截面 - 点击绘制，即可得到截面。

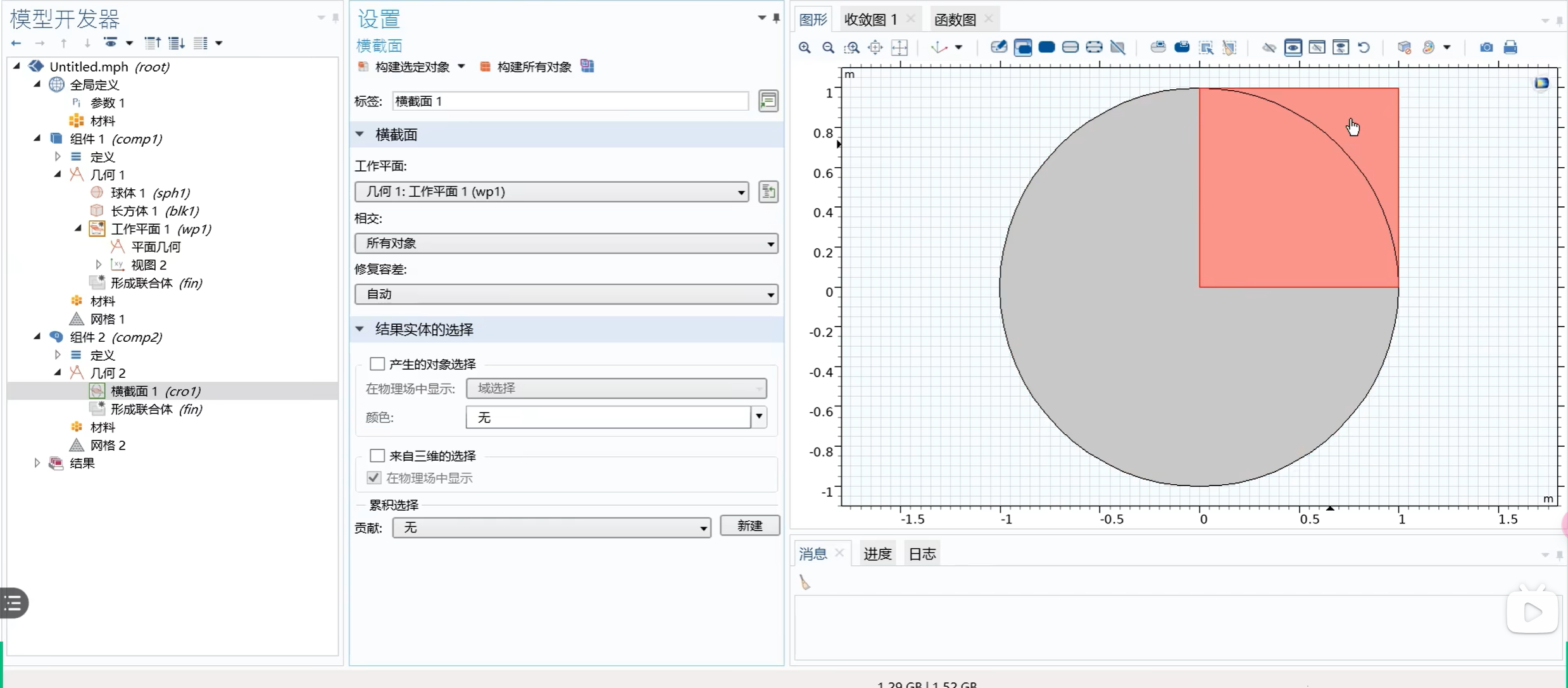
定义层

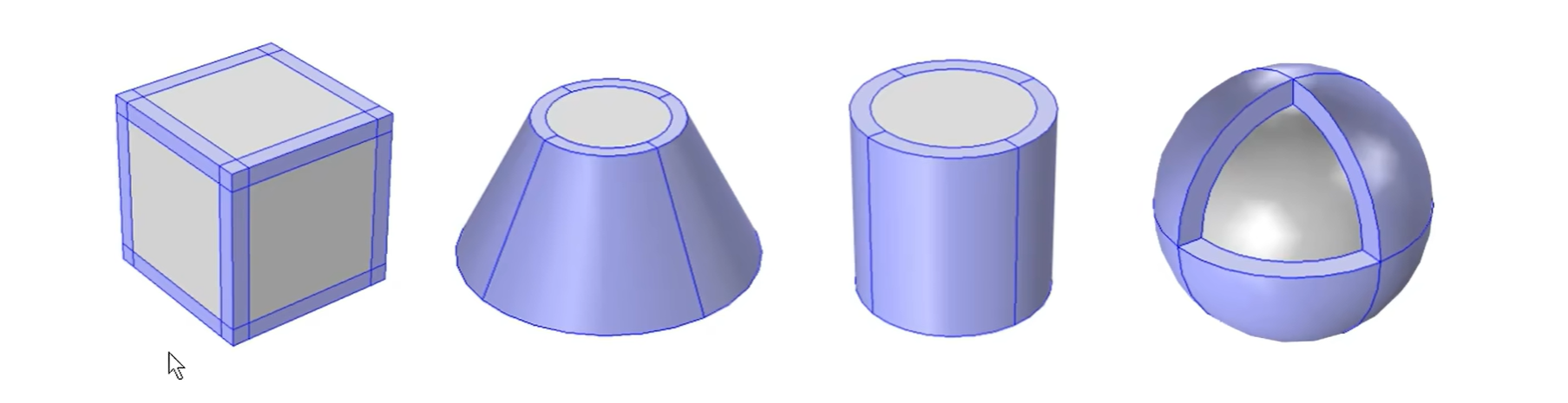
用处：例如完美匹配层（PML），可以用于吸收波（防止传播到无限远处，或是碰到边界发生反射）。

实现方法：直接选中画好的几何体，在 < 层 > 选项下设置层的厚度，然后勾选所有需要层的面。

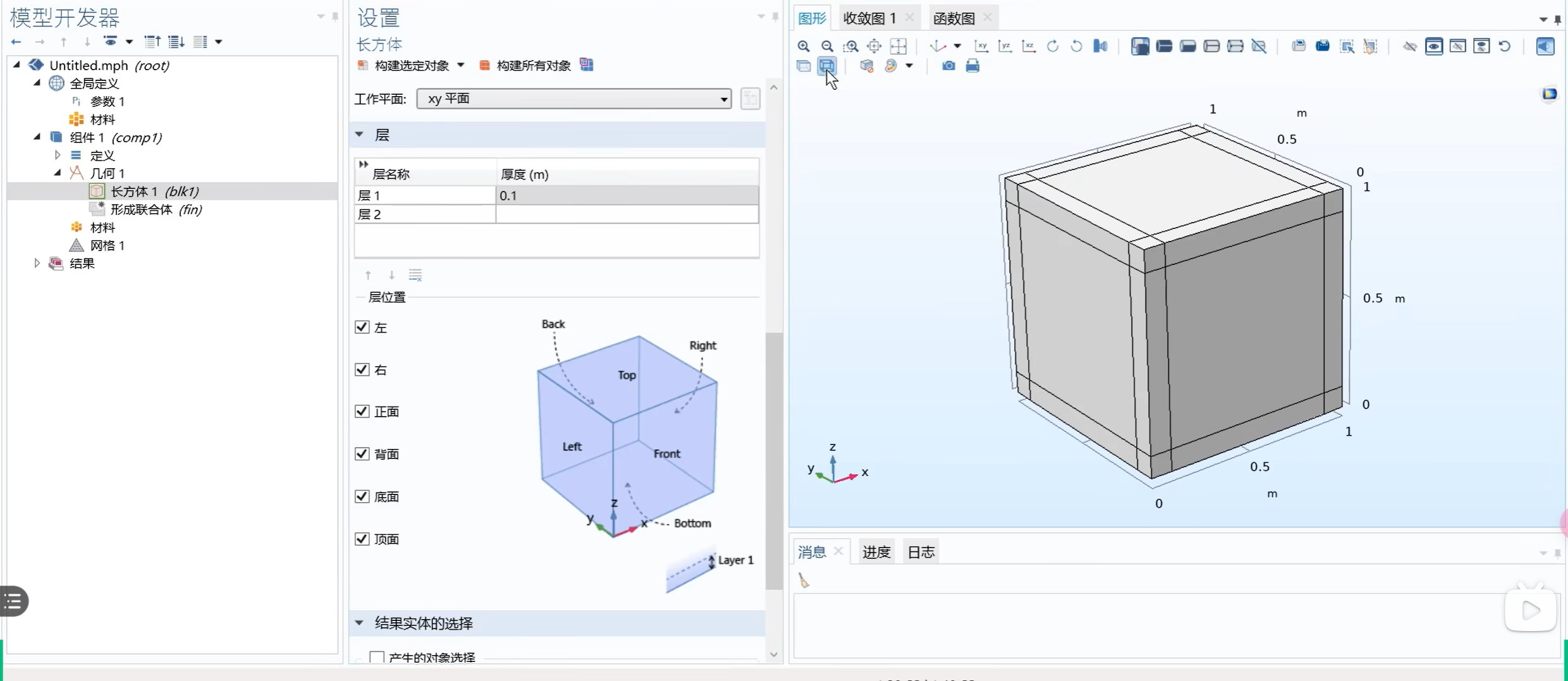
粗糙面

类似于二维。只需要将随机函数的 < 变元数 > 改为 2，并构建“参数化曲面”即可。

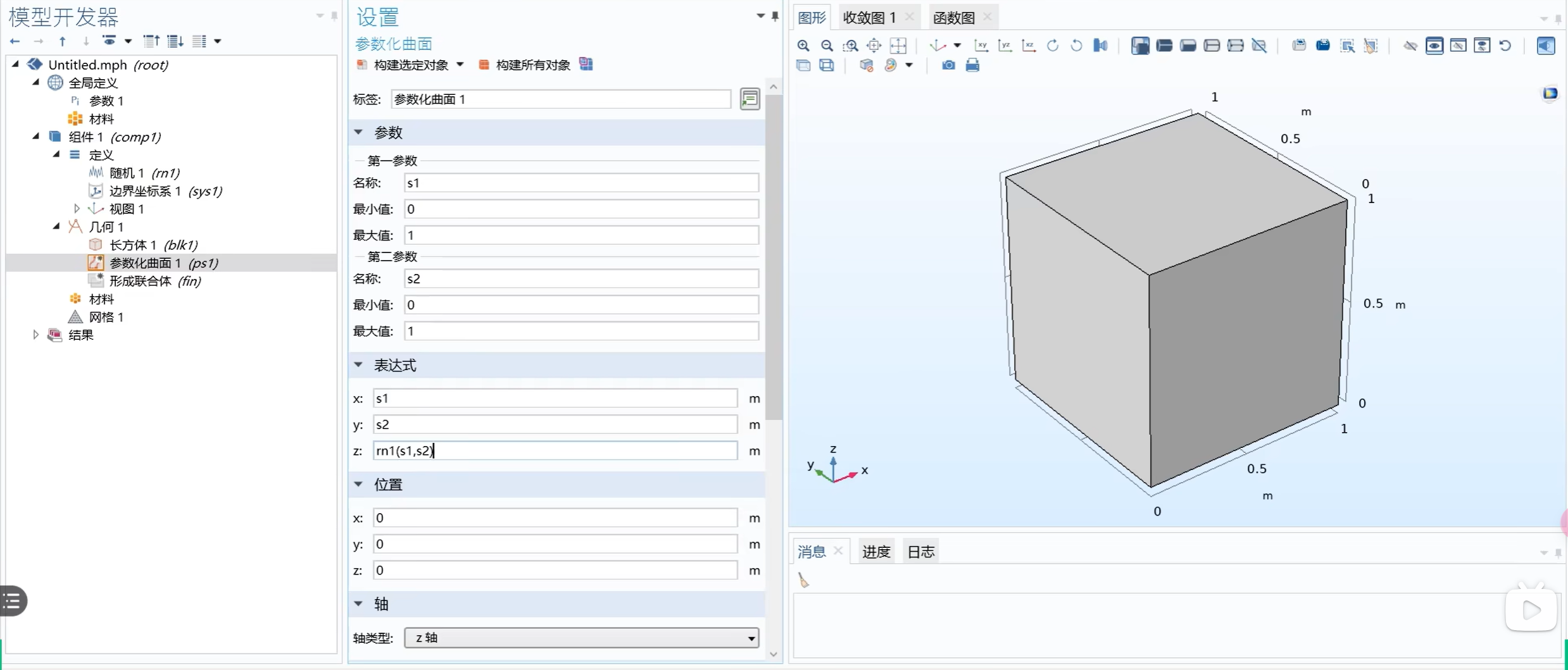
联合体和装配体

联合体：网格（物理量）是连续的。

装配体：网格不连续。

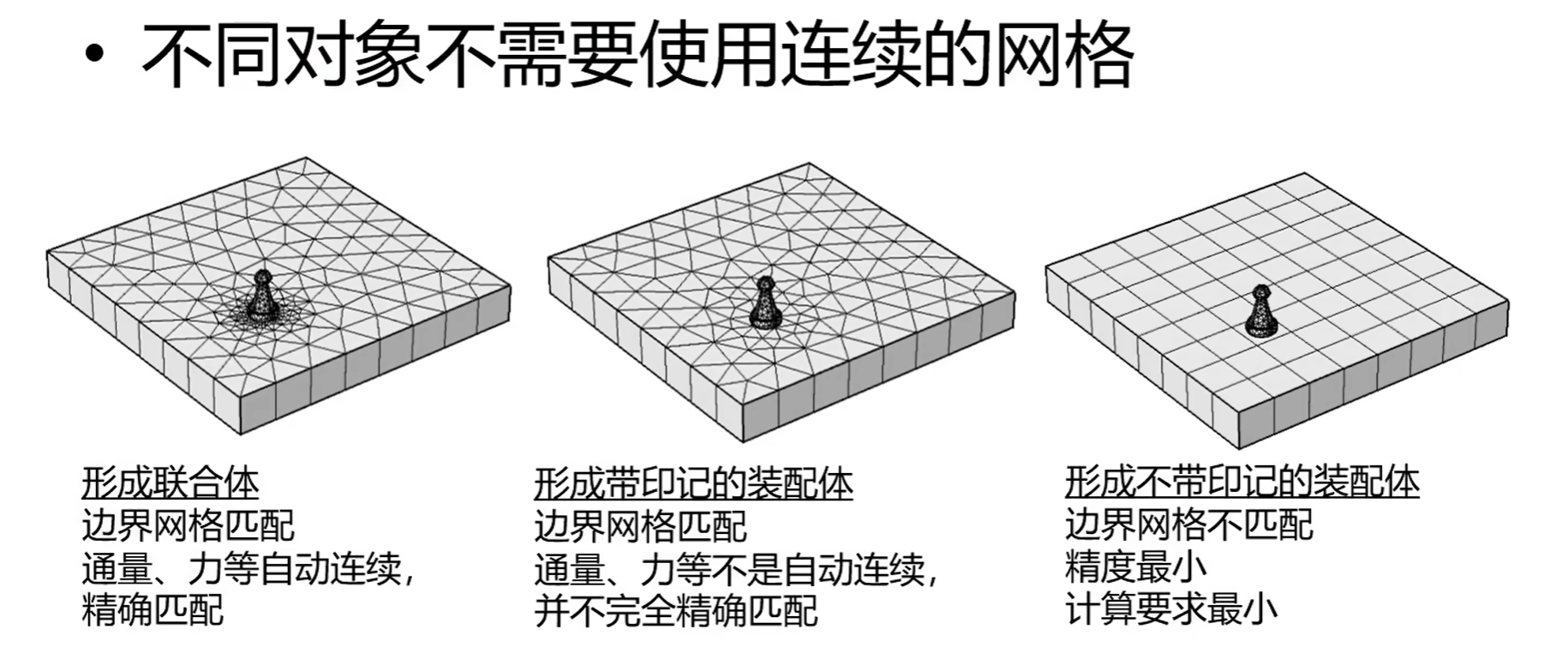
如下情况不能使用装配体：

网格控制顶点 / 边 / 域

网格在此处加密。

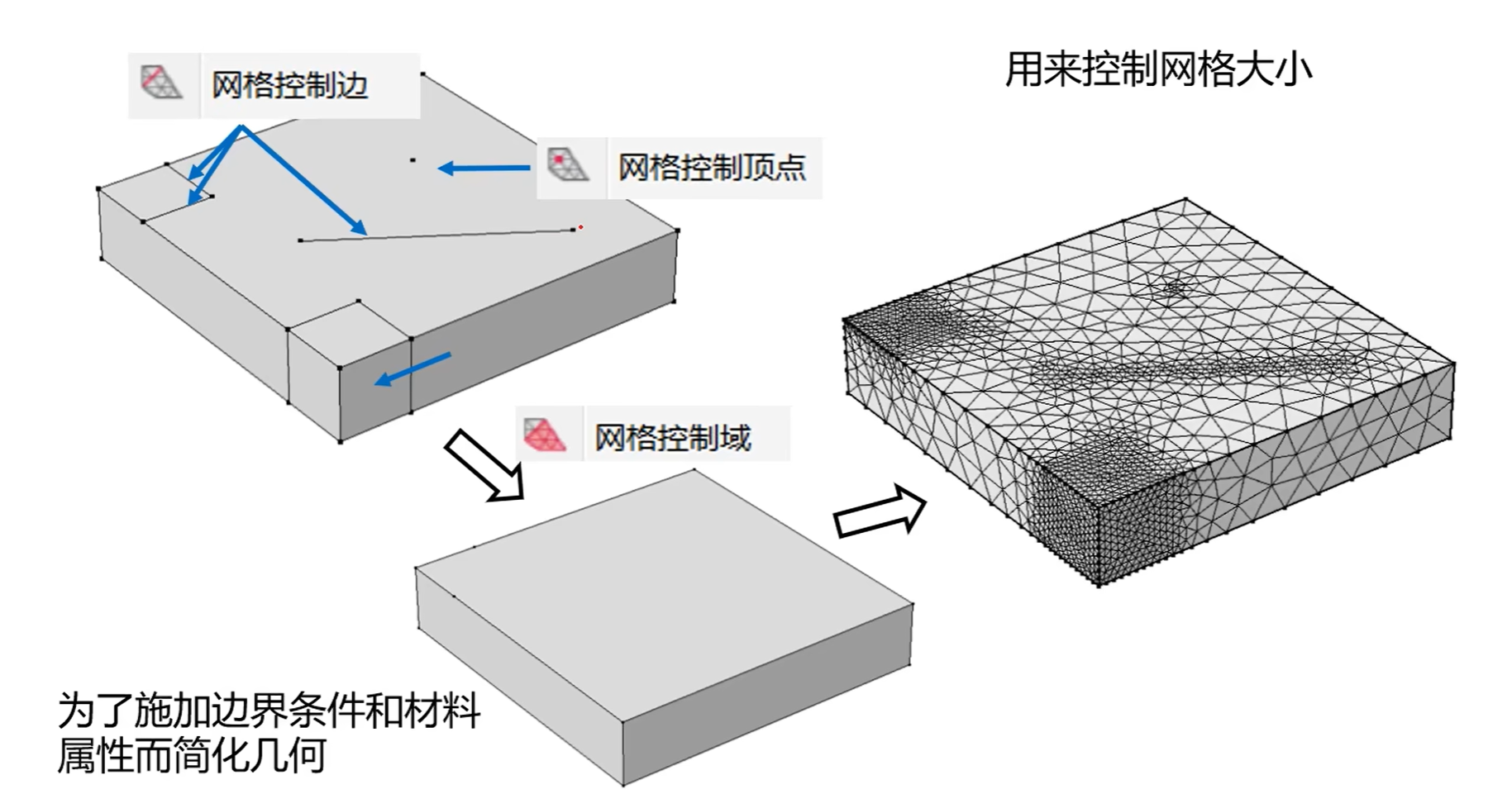
注意事项

1.尽量避免点接触：

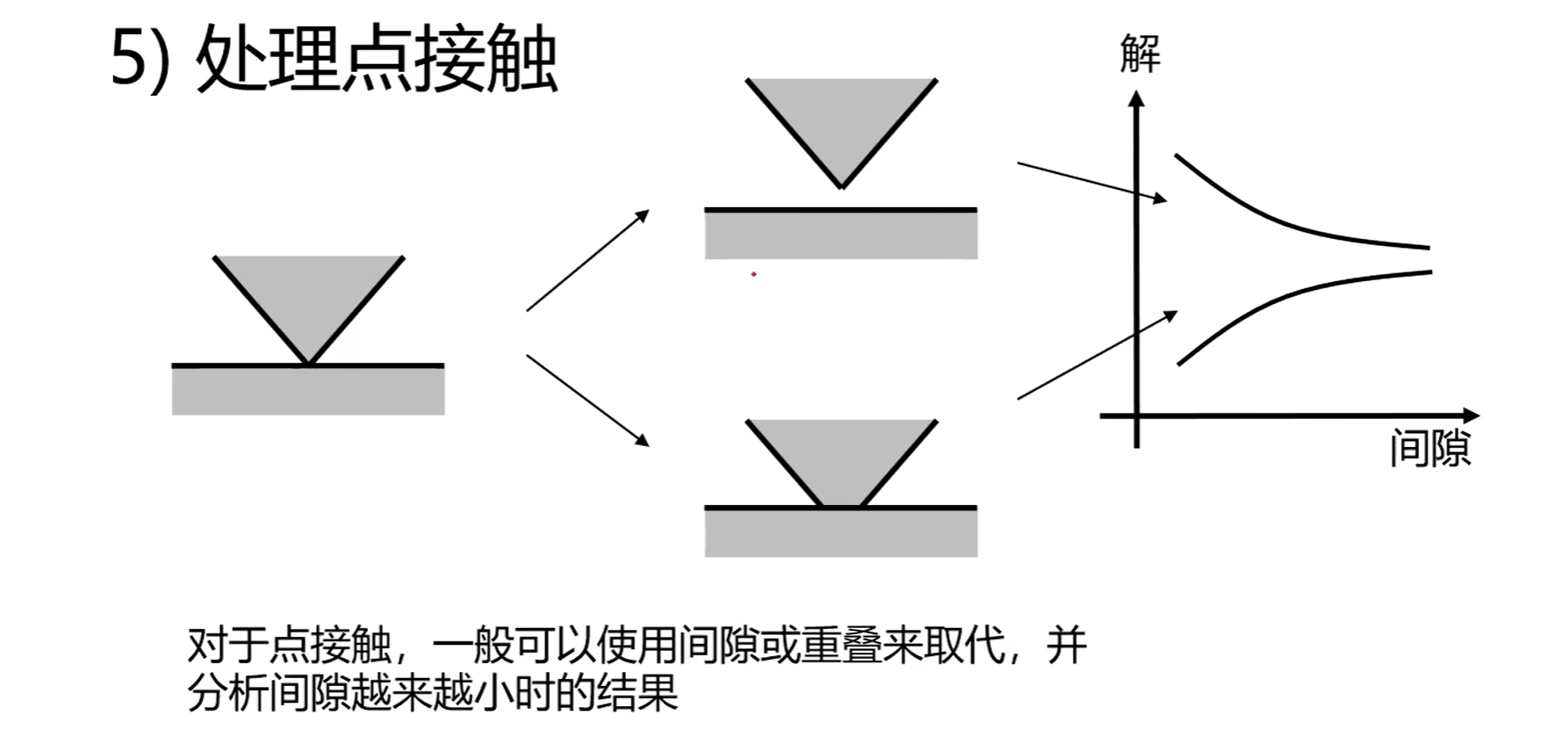
2.适当忽略：

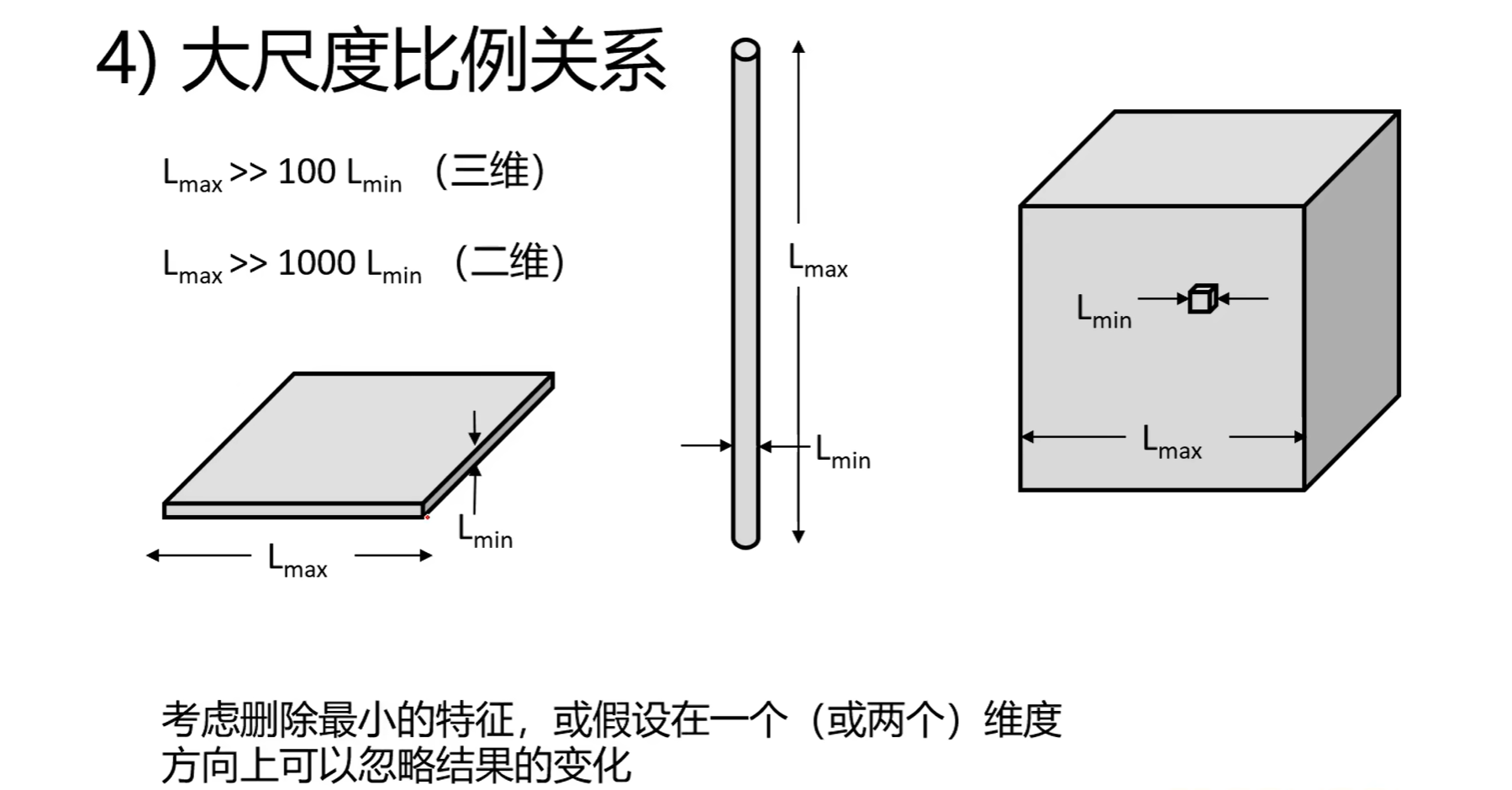
3.薄层结构可以处理为边界：

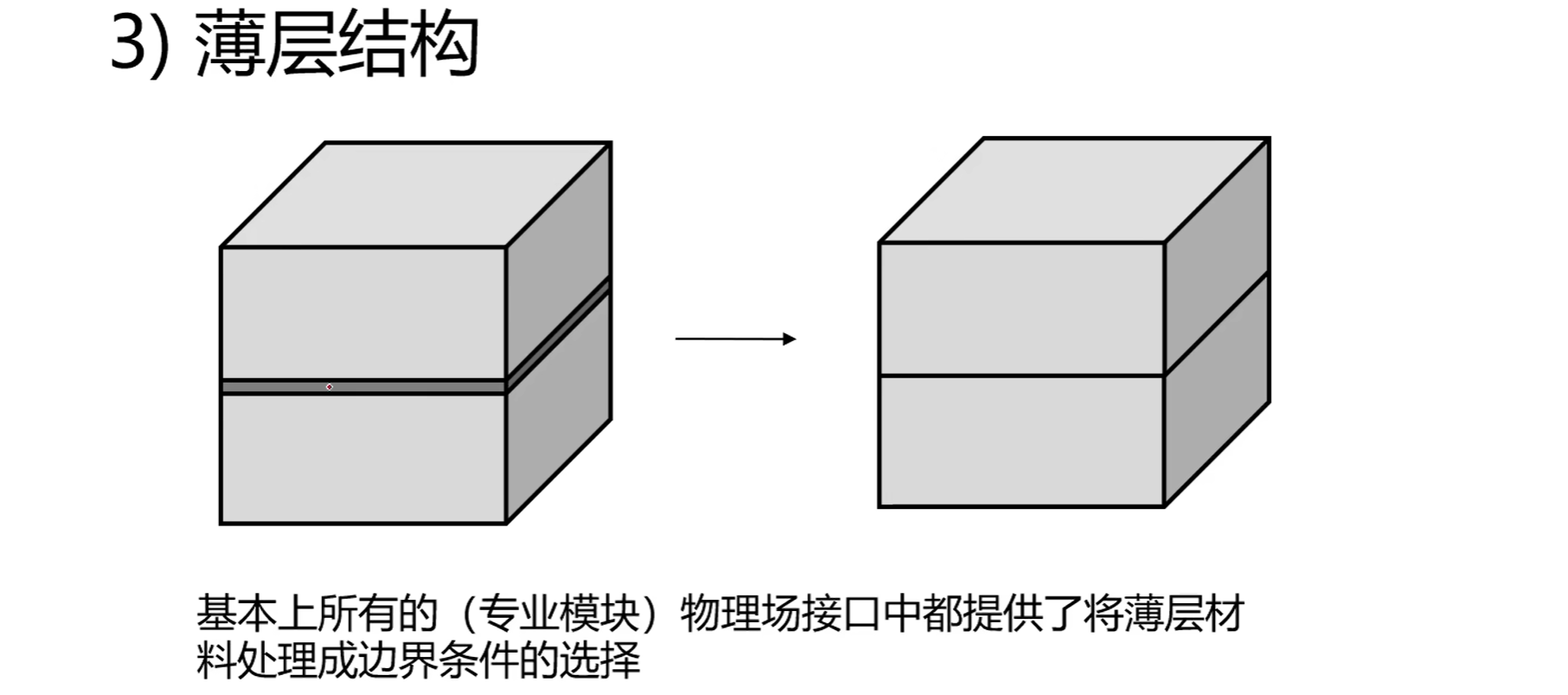
4.简化不必要的细节：

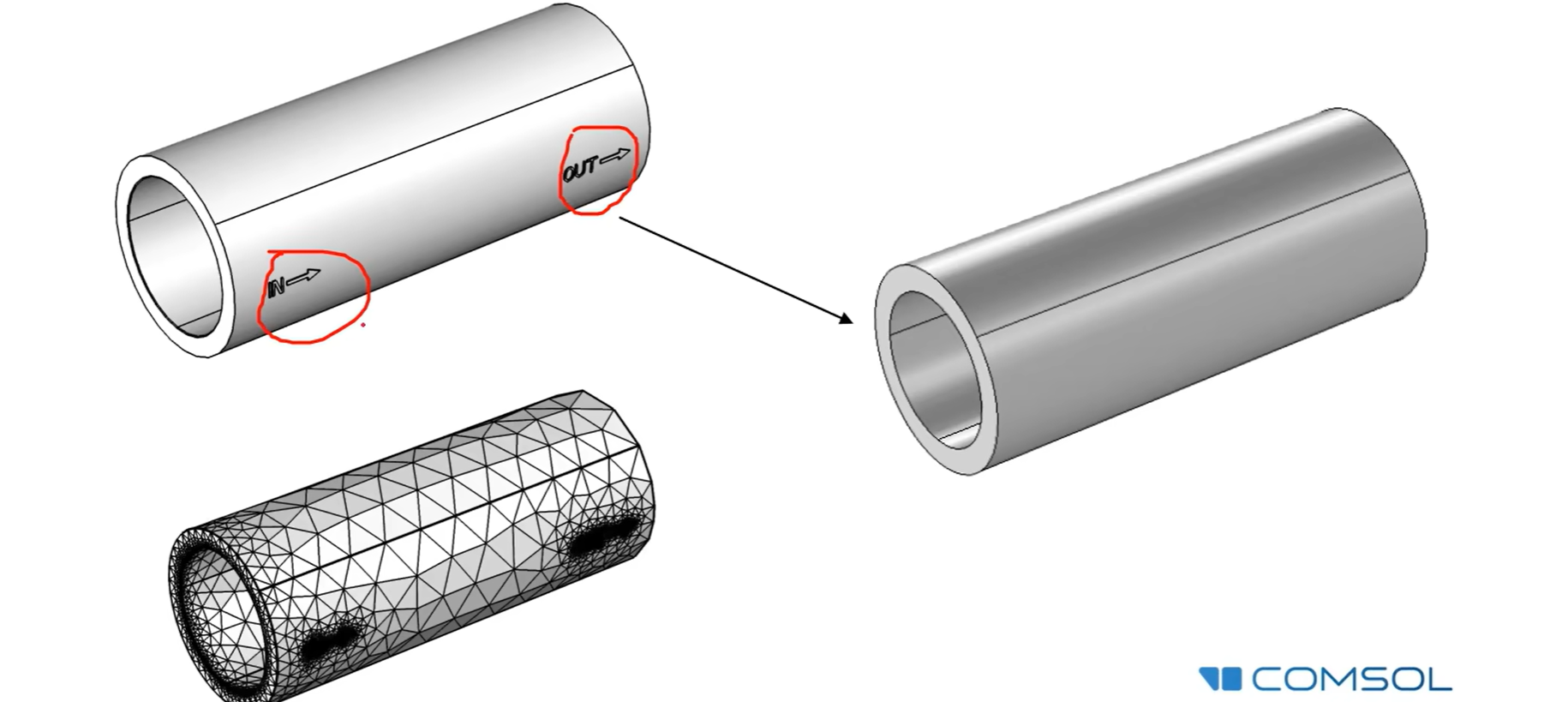
5.处理角部细节：

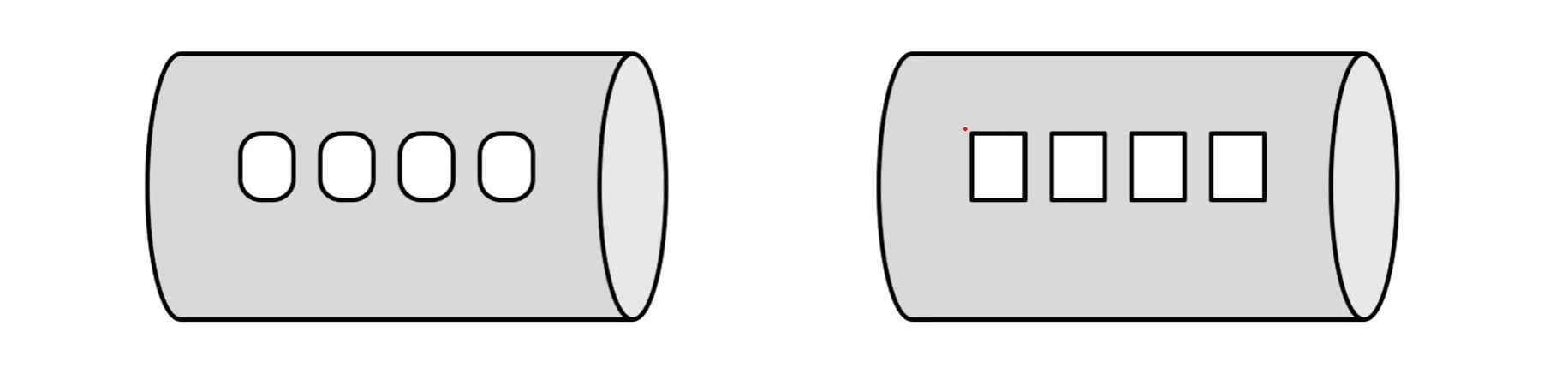
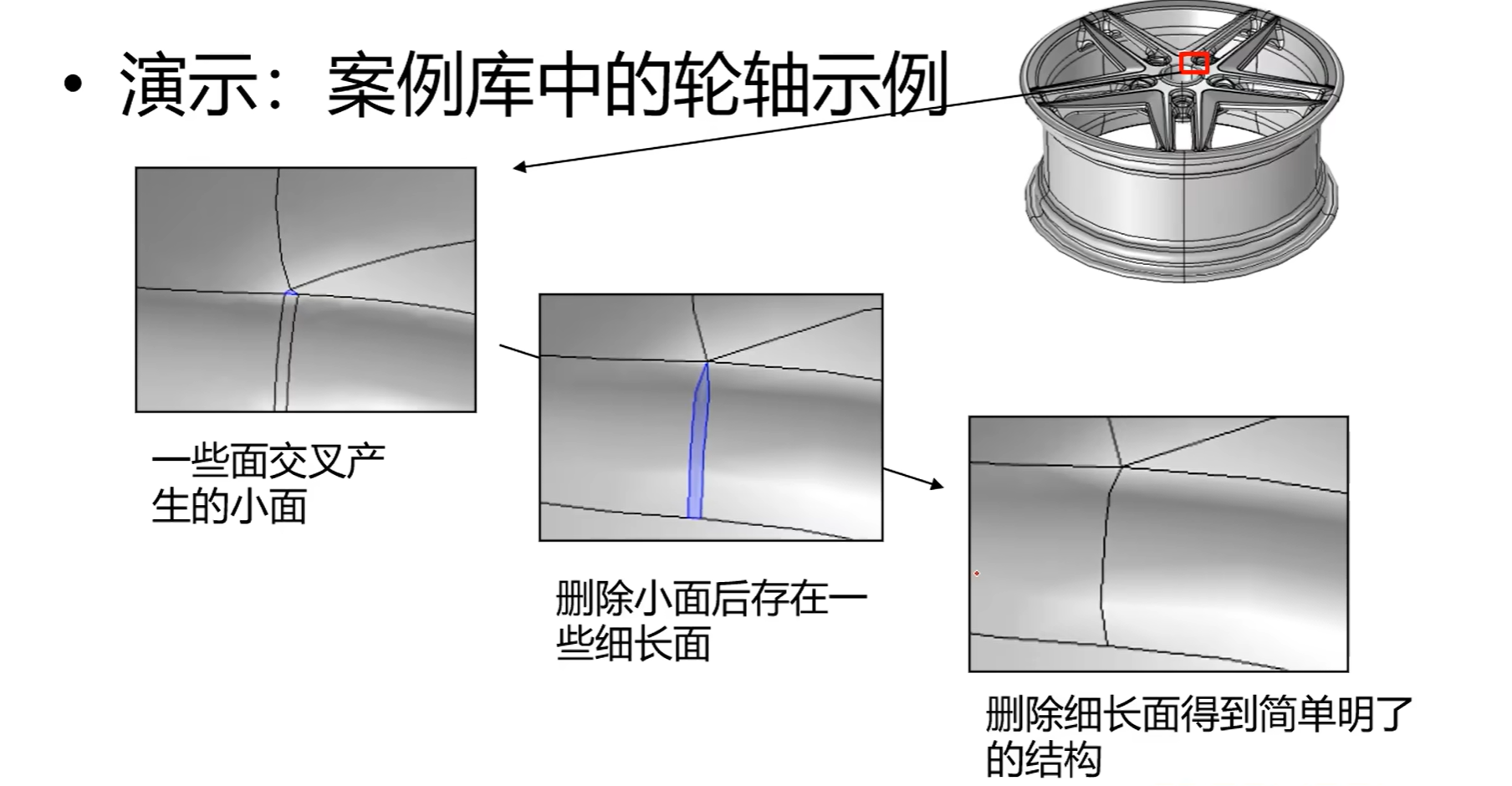
6.删除短边 / 细长面 / 小面 / 楔形

网格

软件通过离散化计算网格顶点的数值，推算其他位置的数值。

基本单元

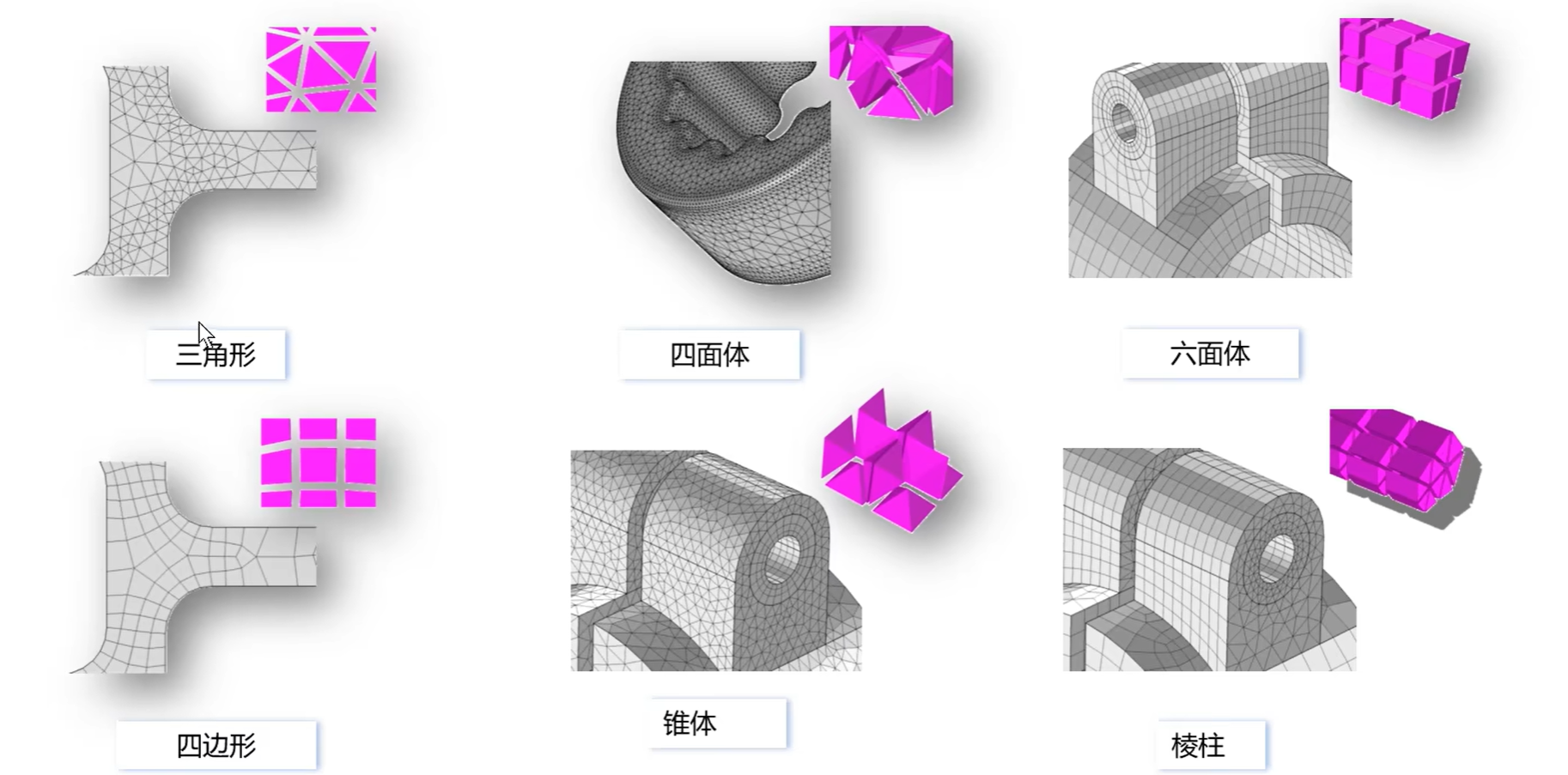
可以对边进行网格剖分。设置边网格剖分的大小可以实现网格在边界上的加密。也可以通过复制边的网格剖分实现周期性边界条件。

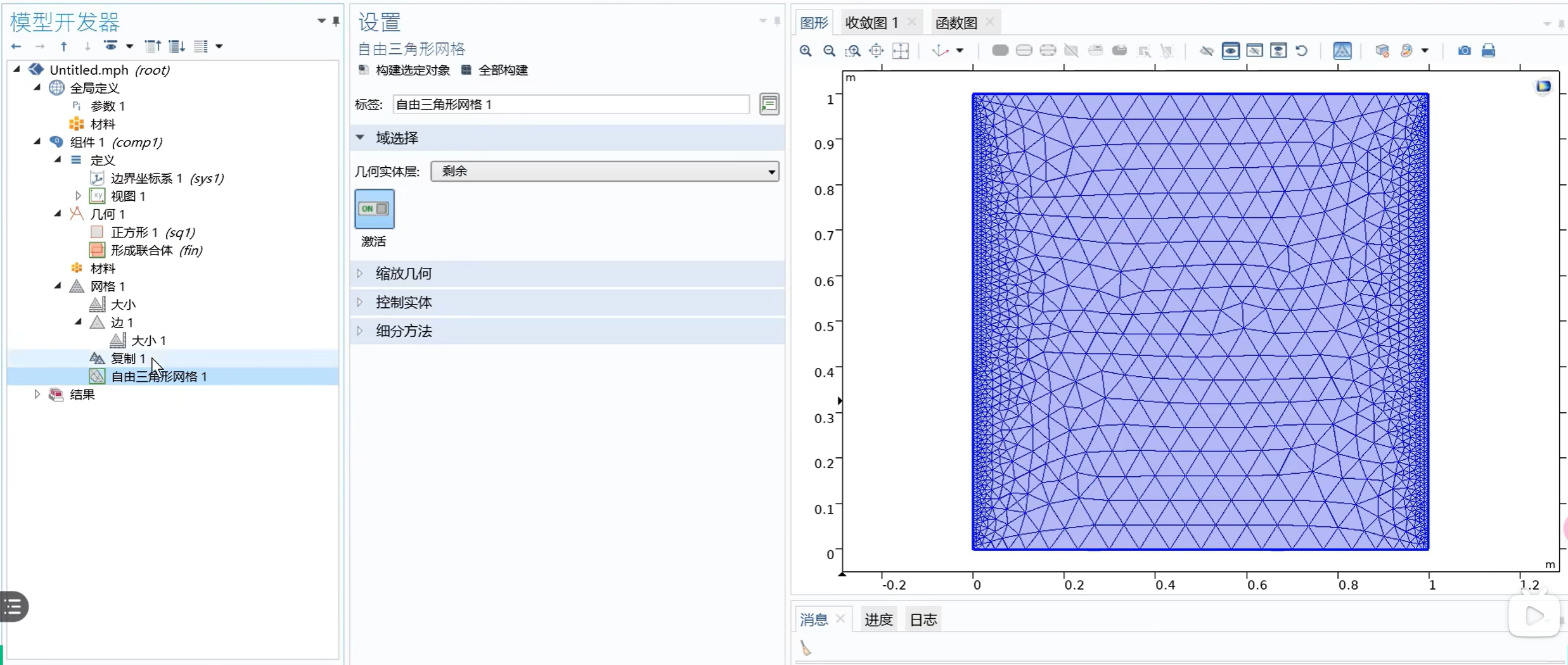
疏密

物理量变化迅速的地方网格较密。

二维

映射网格使用条件：

行函数：移动的波。

二次行函数（除网格顶点外还计算两顶点连线中心的值）：最大网格单元大小 \(≤\frac{λ}{6}\)

一次行函数：最大网格单元大小 \(≤\frac{λ}{12}\)

修改方式：

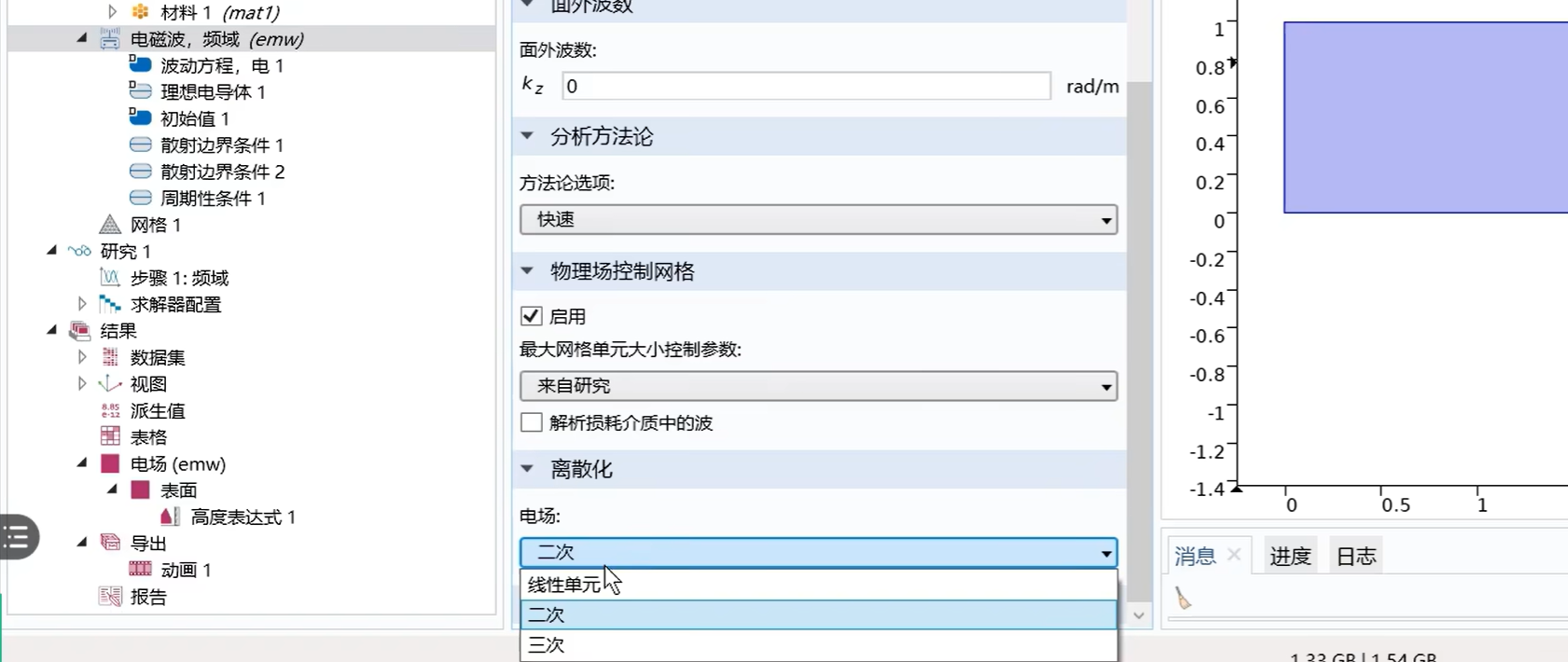
网格大小设定

判断网格的收敛性：

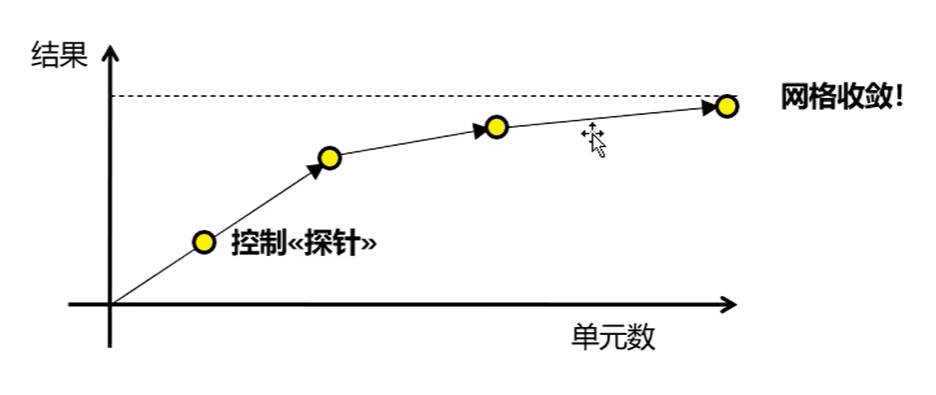
如图所示，可以设置变量 \(h1\)，定义网格最大长度 \(= λ / h1\) （\(λ\) 是事先定义好的波长）。对 \(h1\) 进行参数化扫描，逐个查看 \(h1\) 的值对应的结果，找到收敛时的最小 \(h1\).

更直观地，我们可以设置一个截点，对截点的结果进行绘图，直接在曲线上找到收敛点。

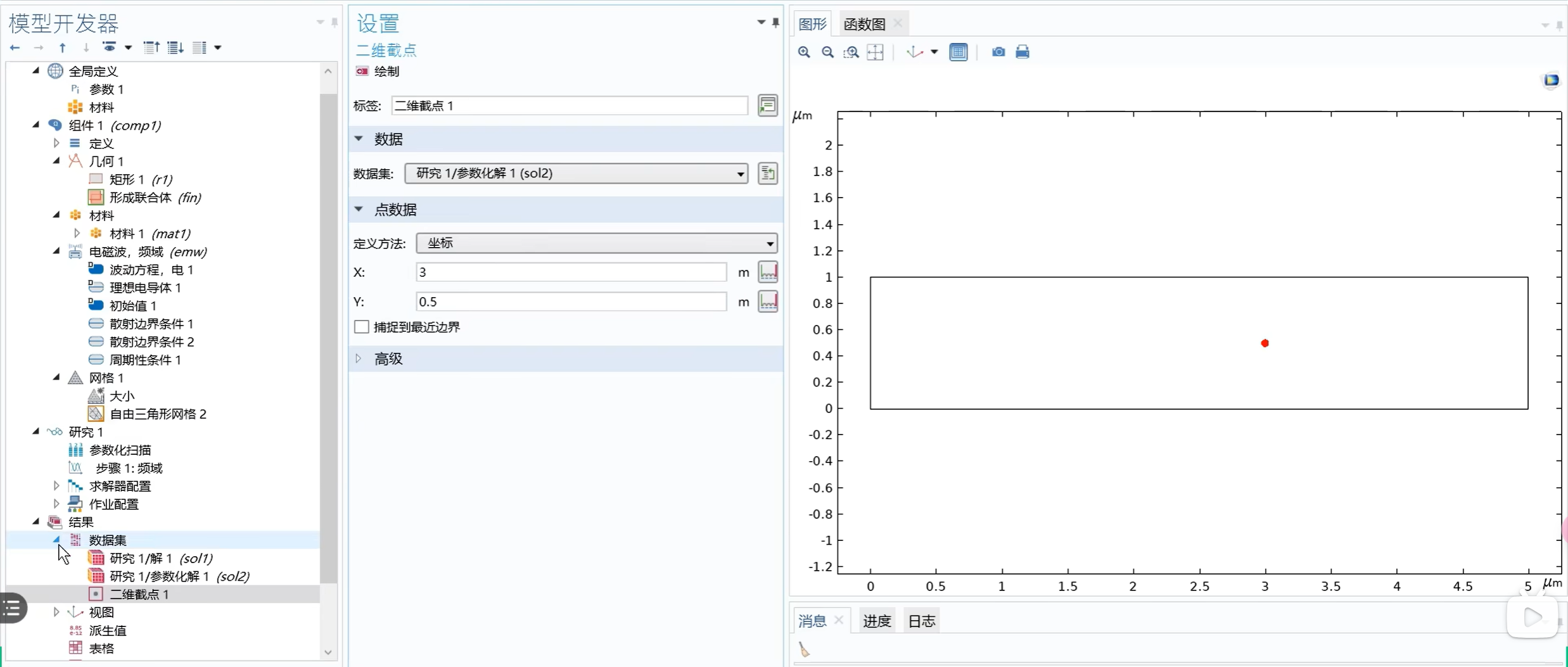
选择一维绘图组 - 点结果图，将 \(h1\) 设置为横轴，电场强度设置为纵轴，即可查看曲线。

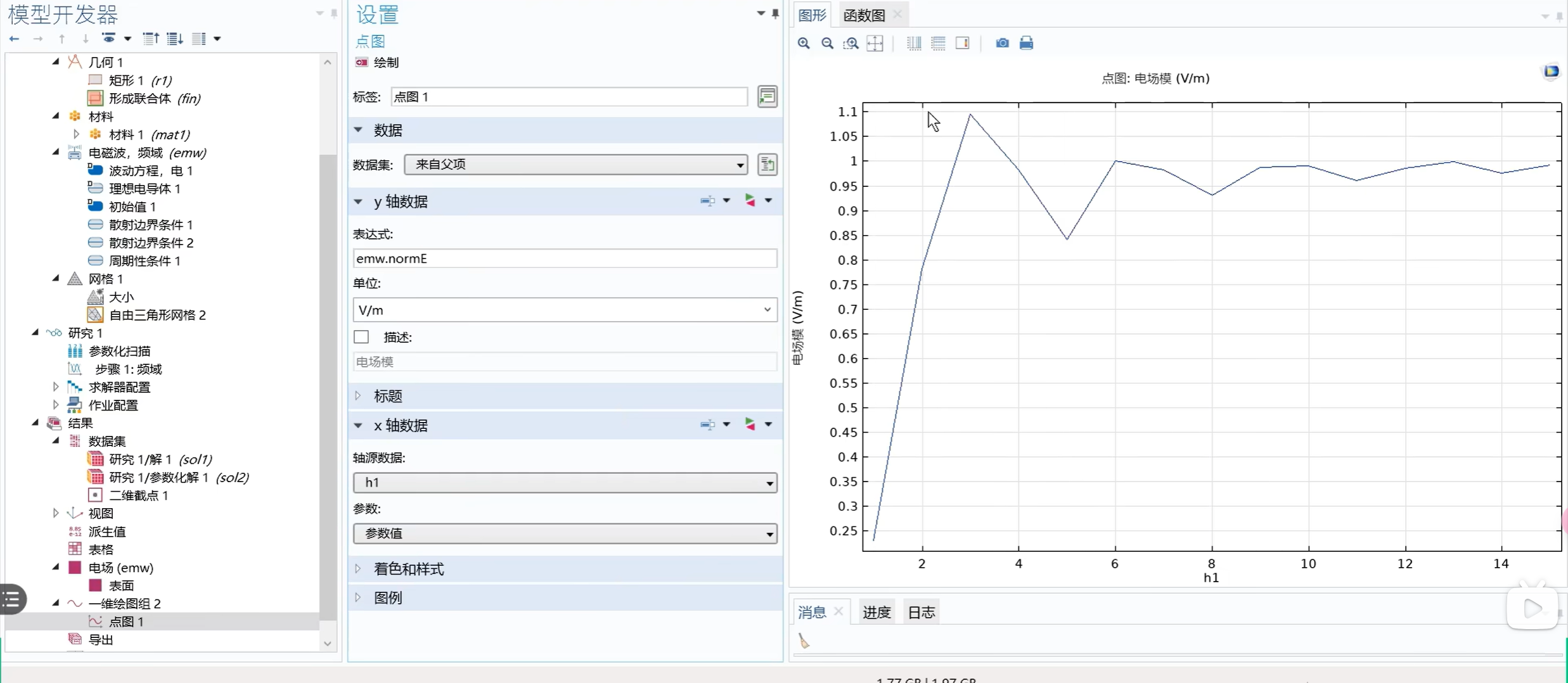
三维网格的质量判断

方法一：

右键 < 网格 > ，点击 < 绘制 > ：

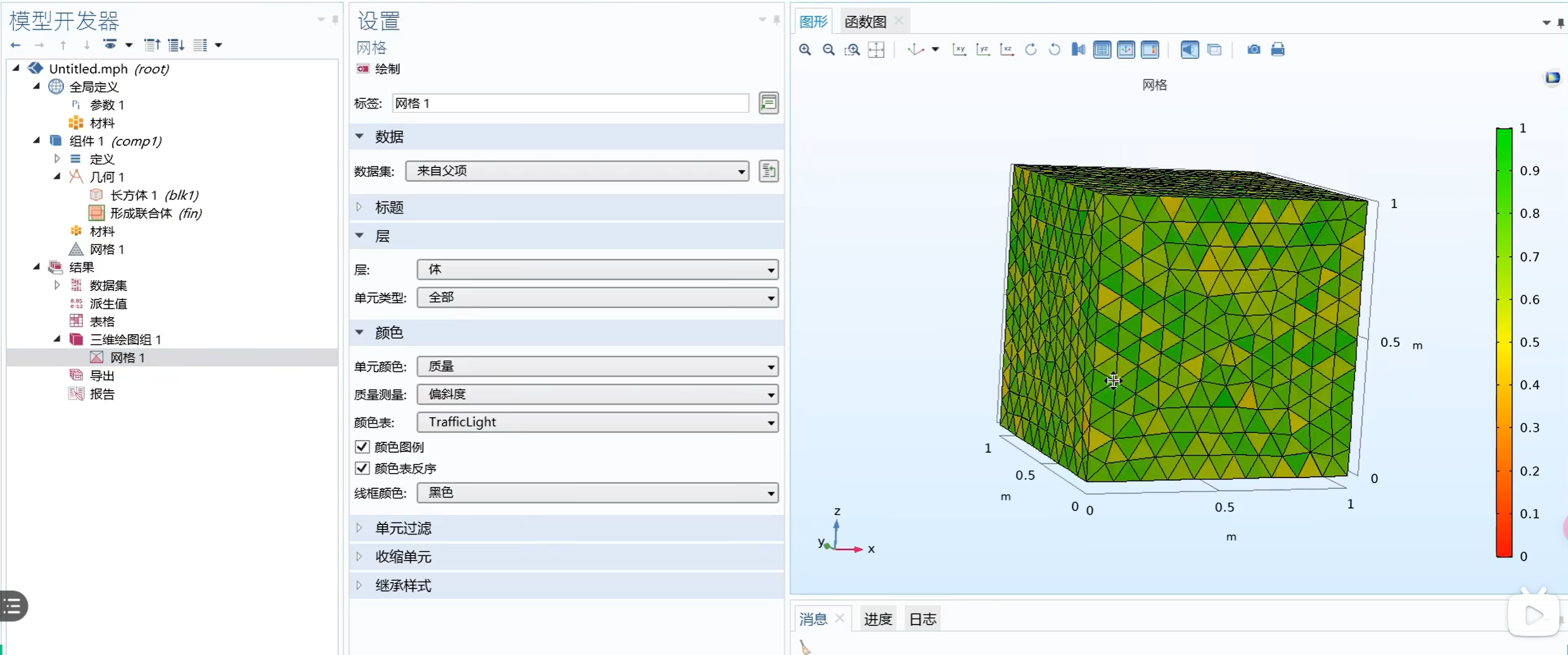
颜色越绿，代表网格的质量越好。

点击 < 启用过滤 > 按钮，例如选择 x > 0.5，可以查看几何体内部网格情况。也可以设置网格收缩因子。

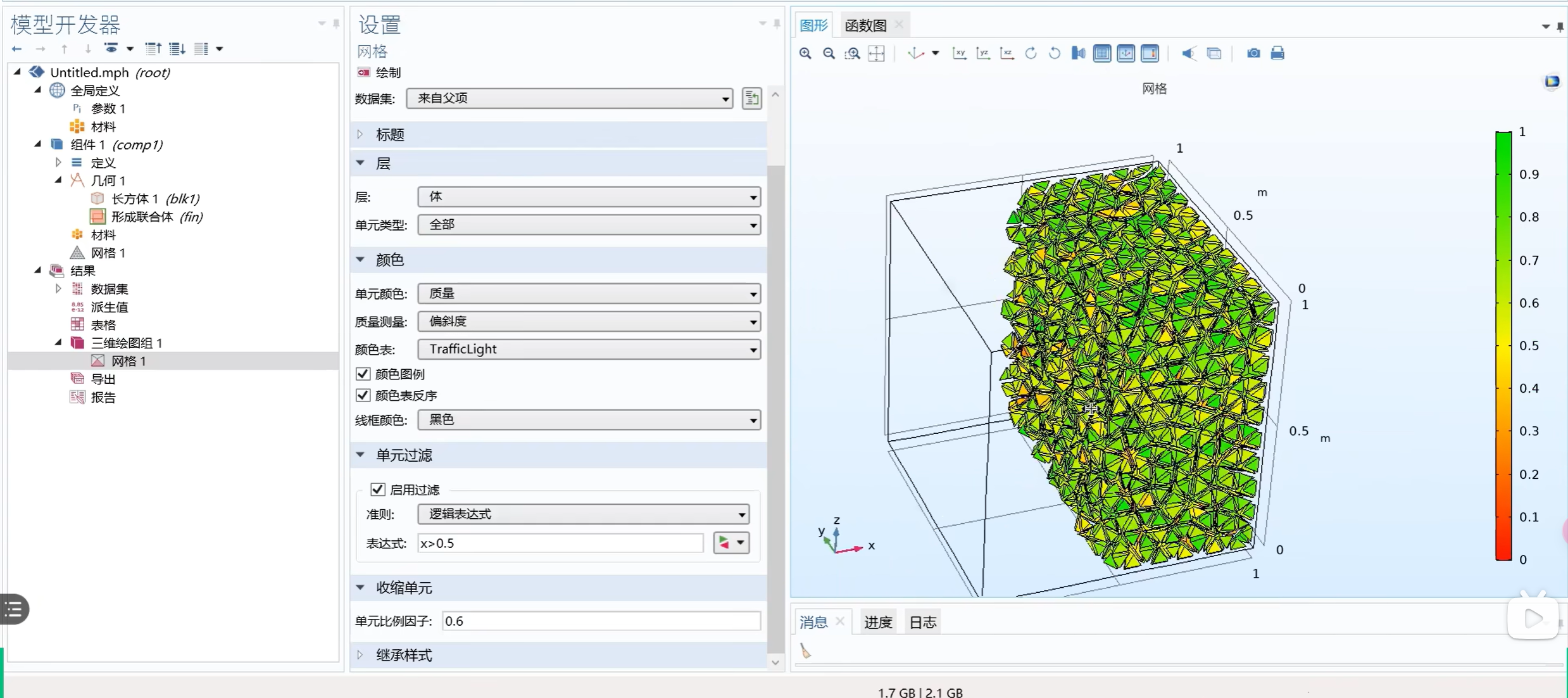
方法二：

右键 < 网格 > ，点击 < 统计信息 >，找到最下面的柱状图：

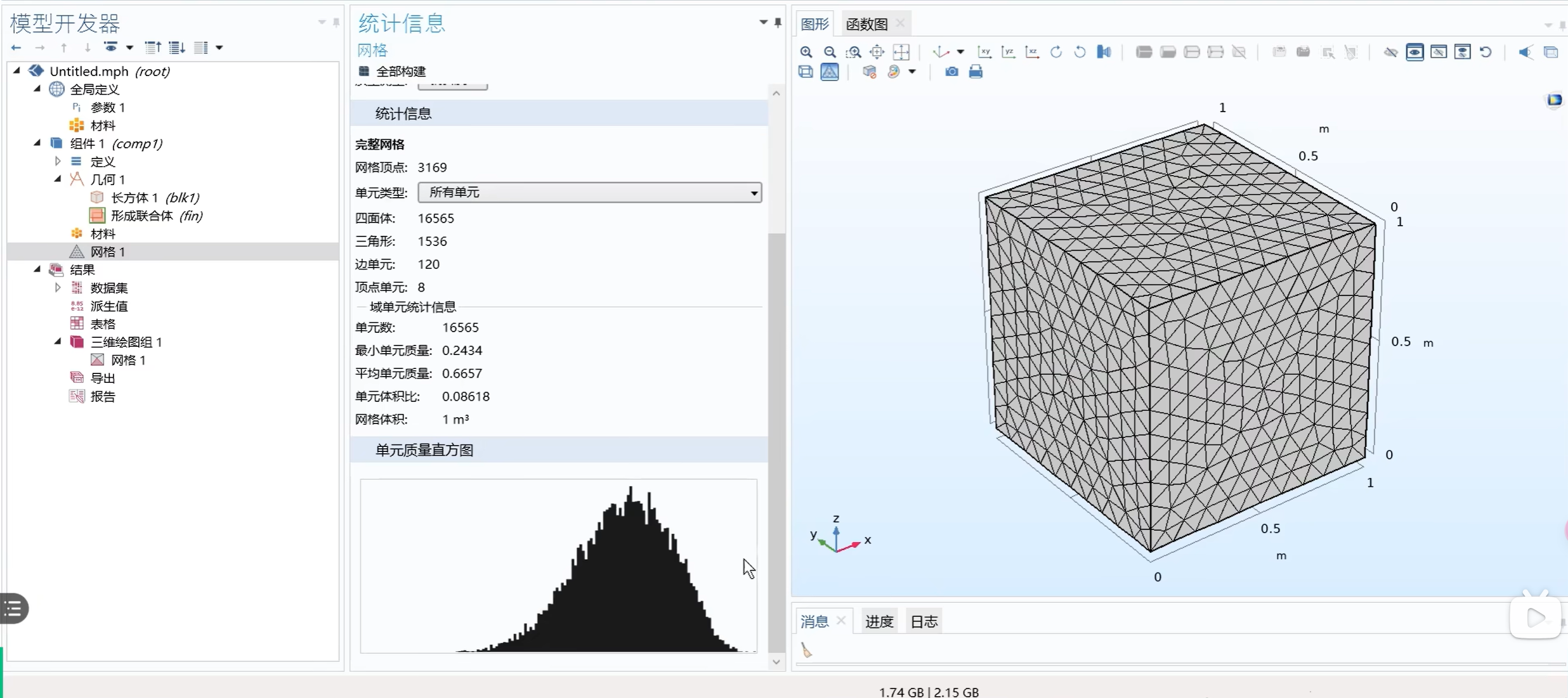
整体趋势越往右偏，代表网格的质量越好。

当几何体规整时，网格类型可以选用“扫掠”（类似于二维的“映射”）。得到的网格质量较高。

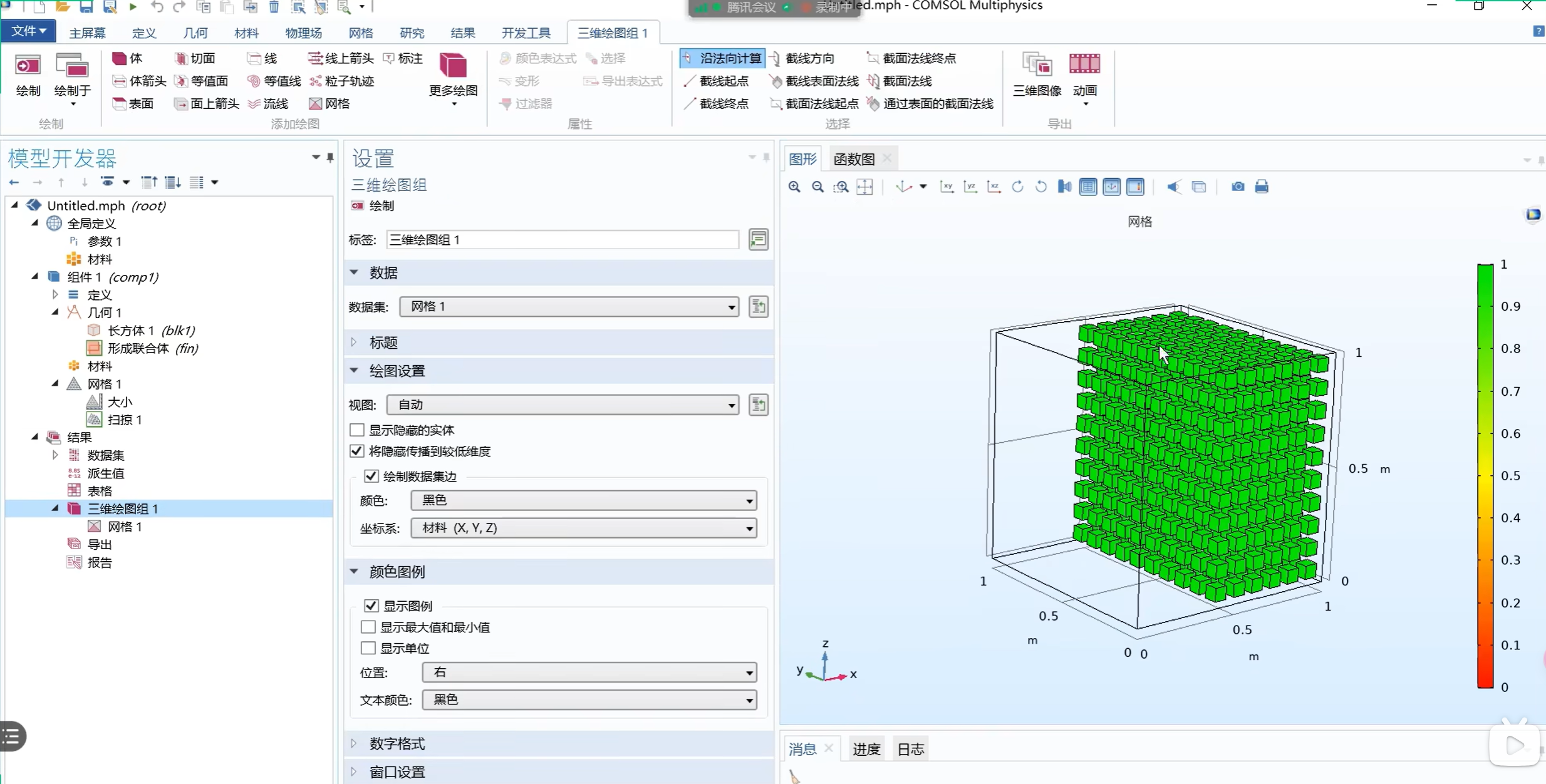
扫掠网格使用条件：

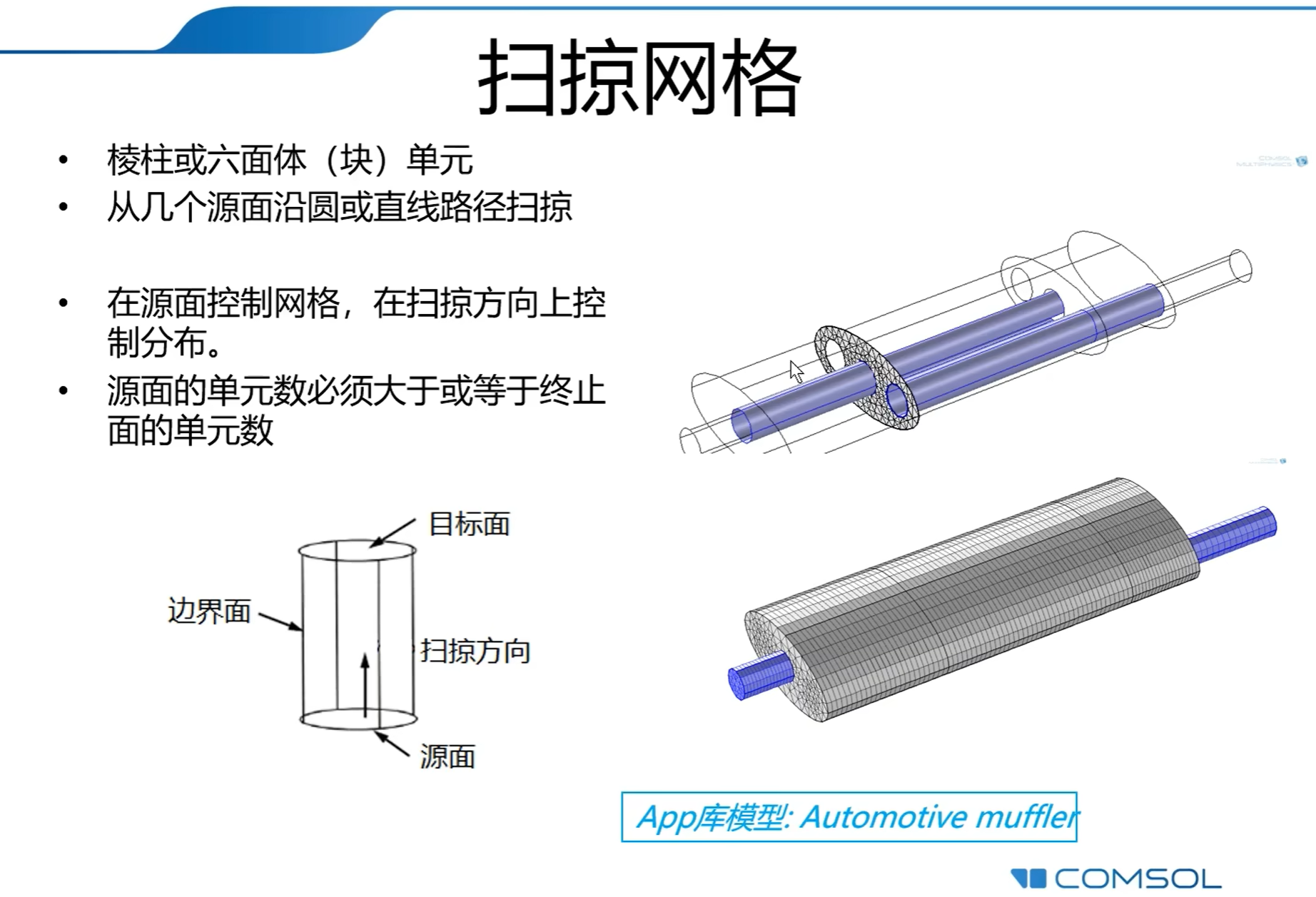
研究类型及求解器

后处理

结果节点结构

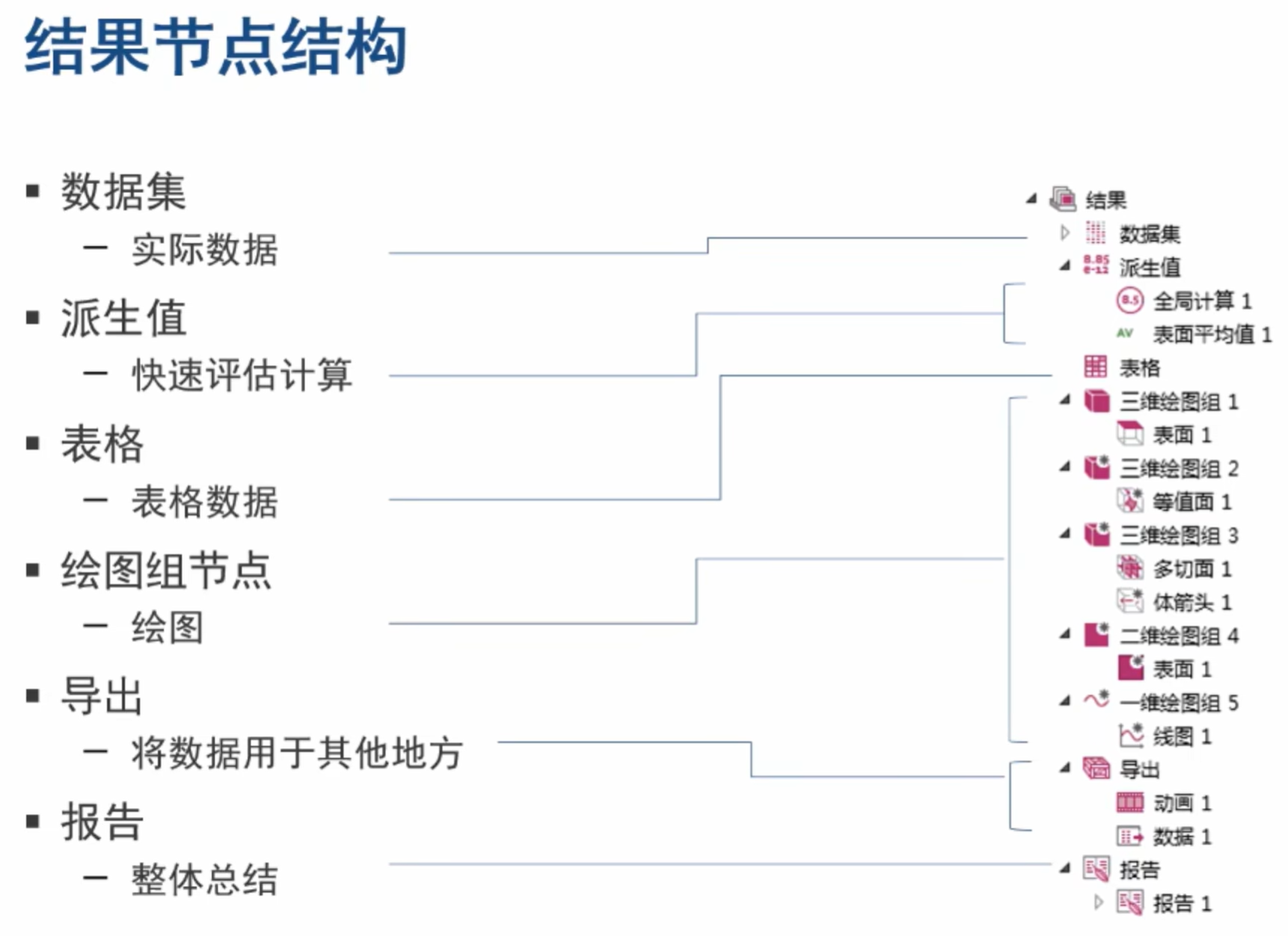
数据集

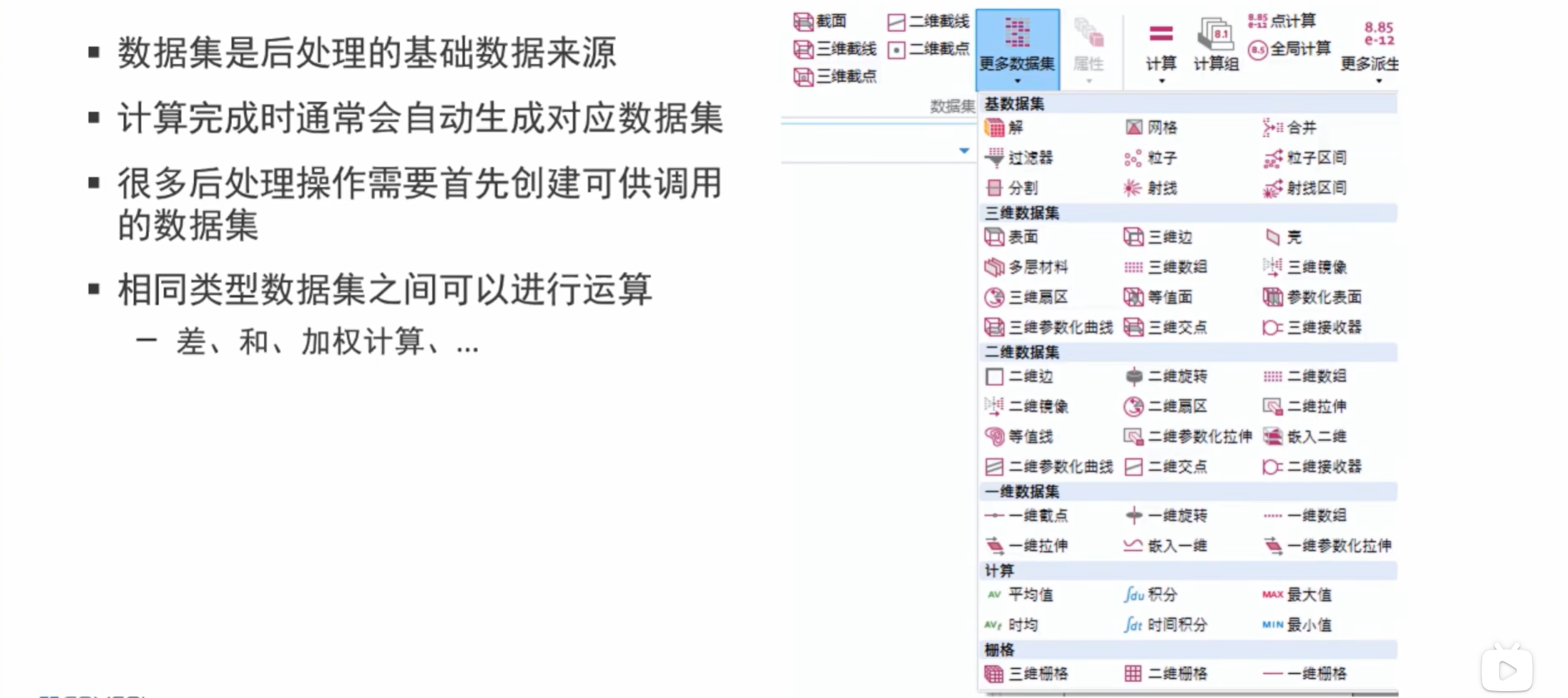
其中“解”是任何模型计算完成之后都会生成的。

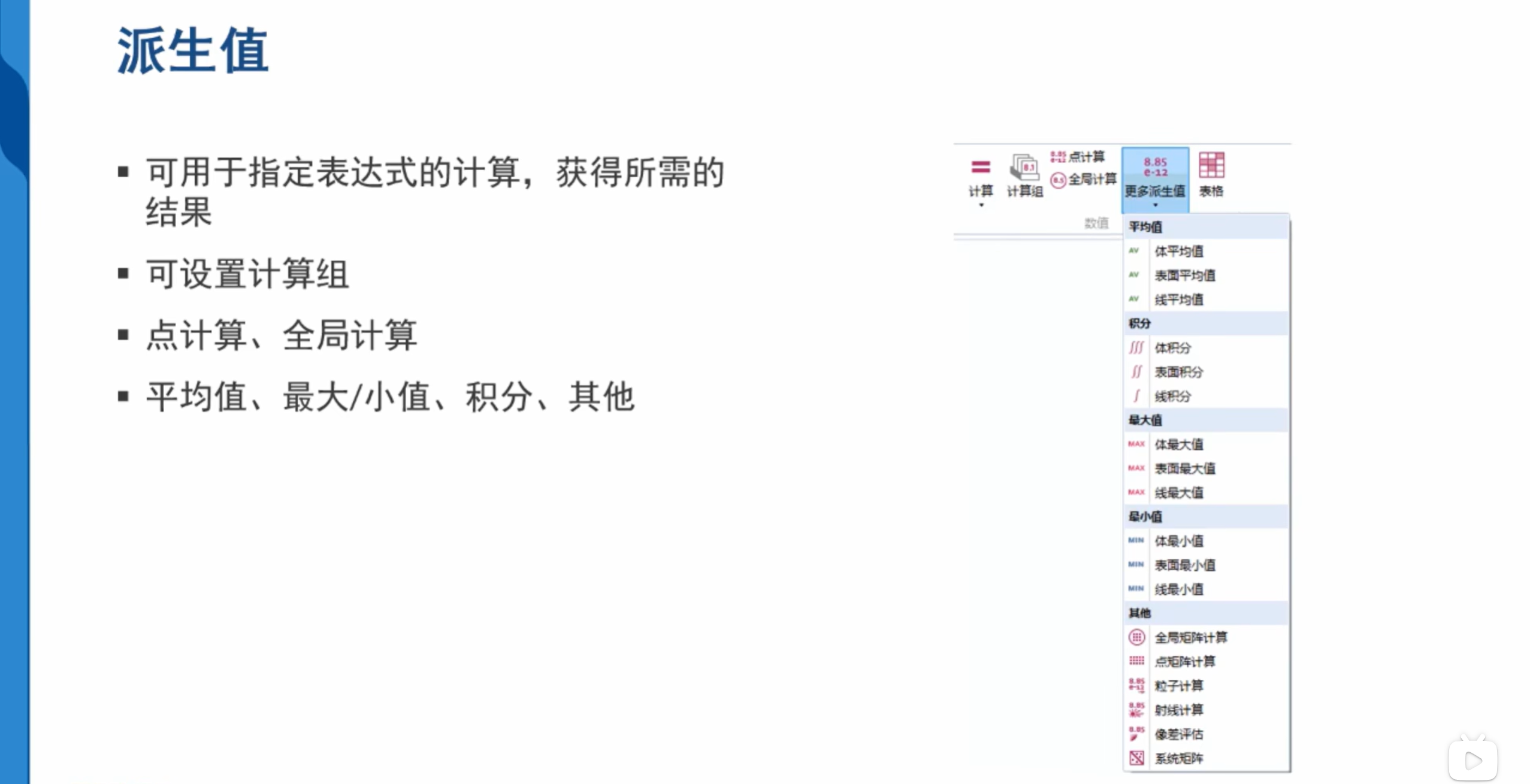
派生值及表格

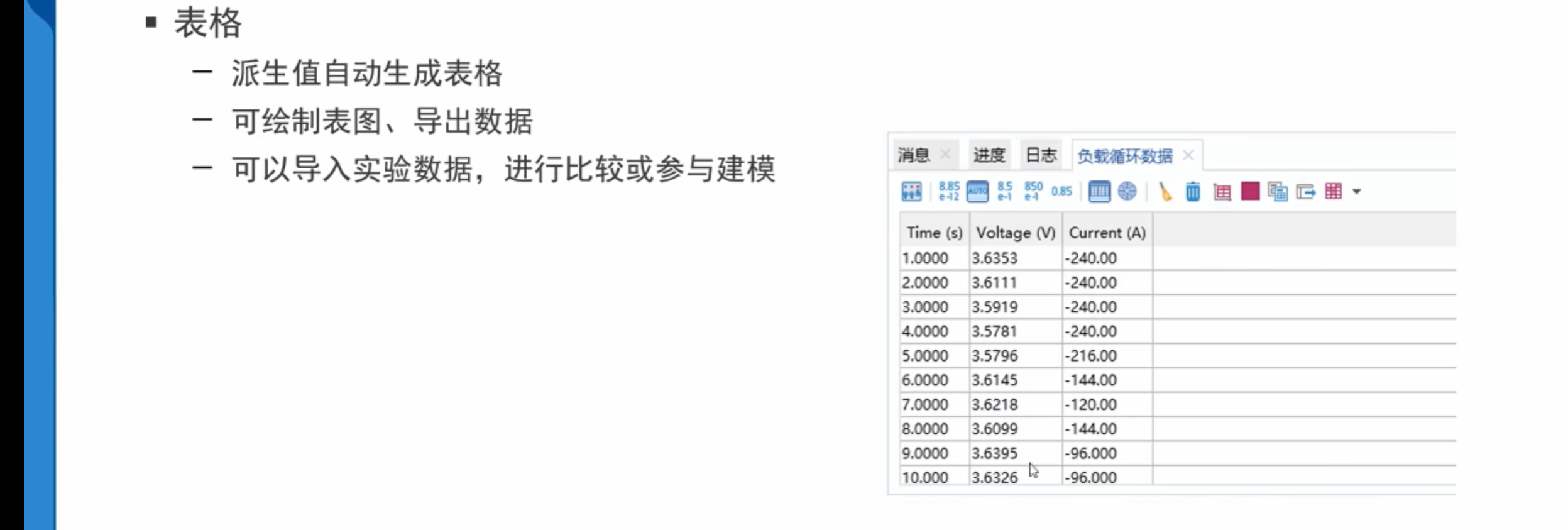
绘图组

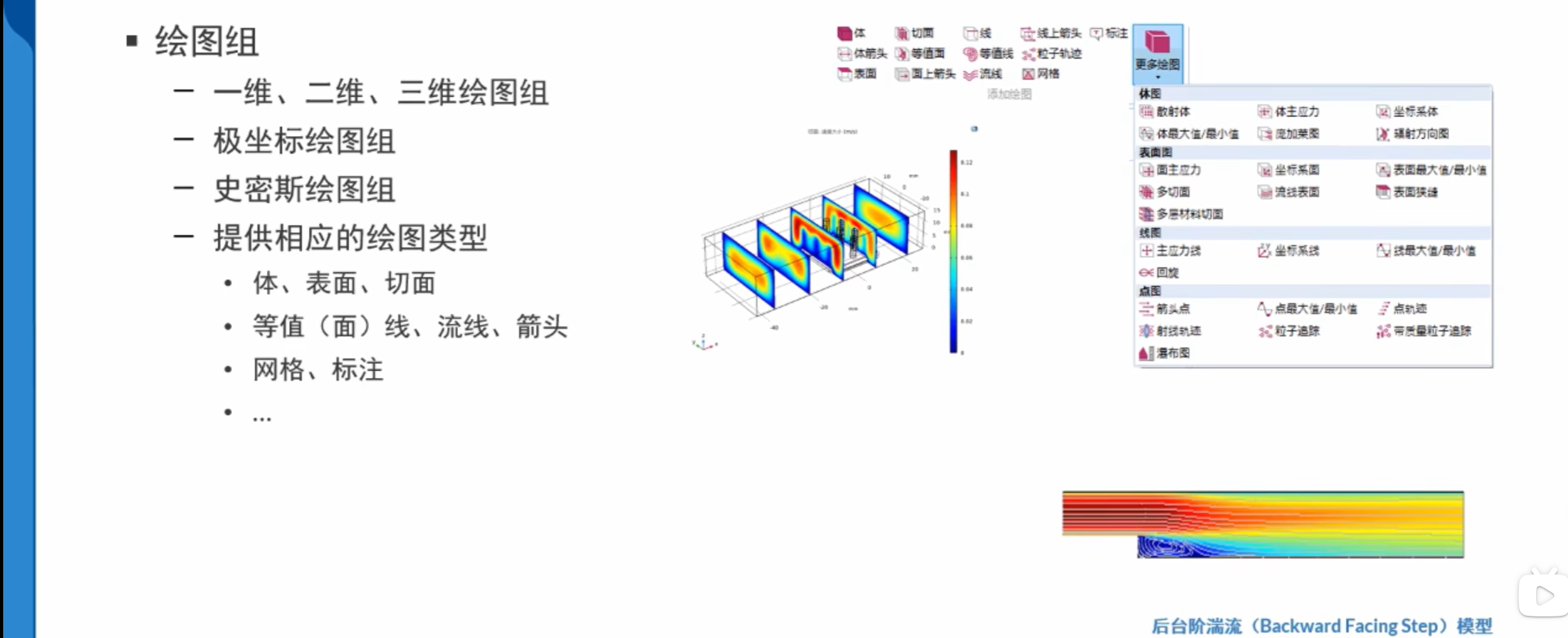
绘图类型

截线 / 截面与截点同理。

流线图相当于绘制轨迹。

导出

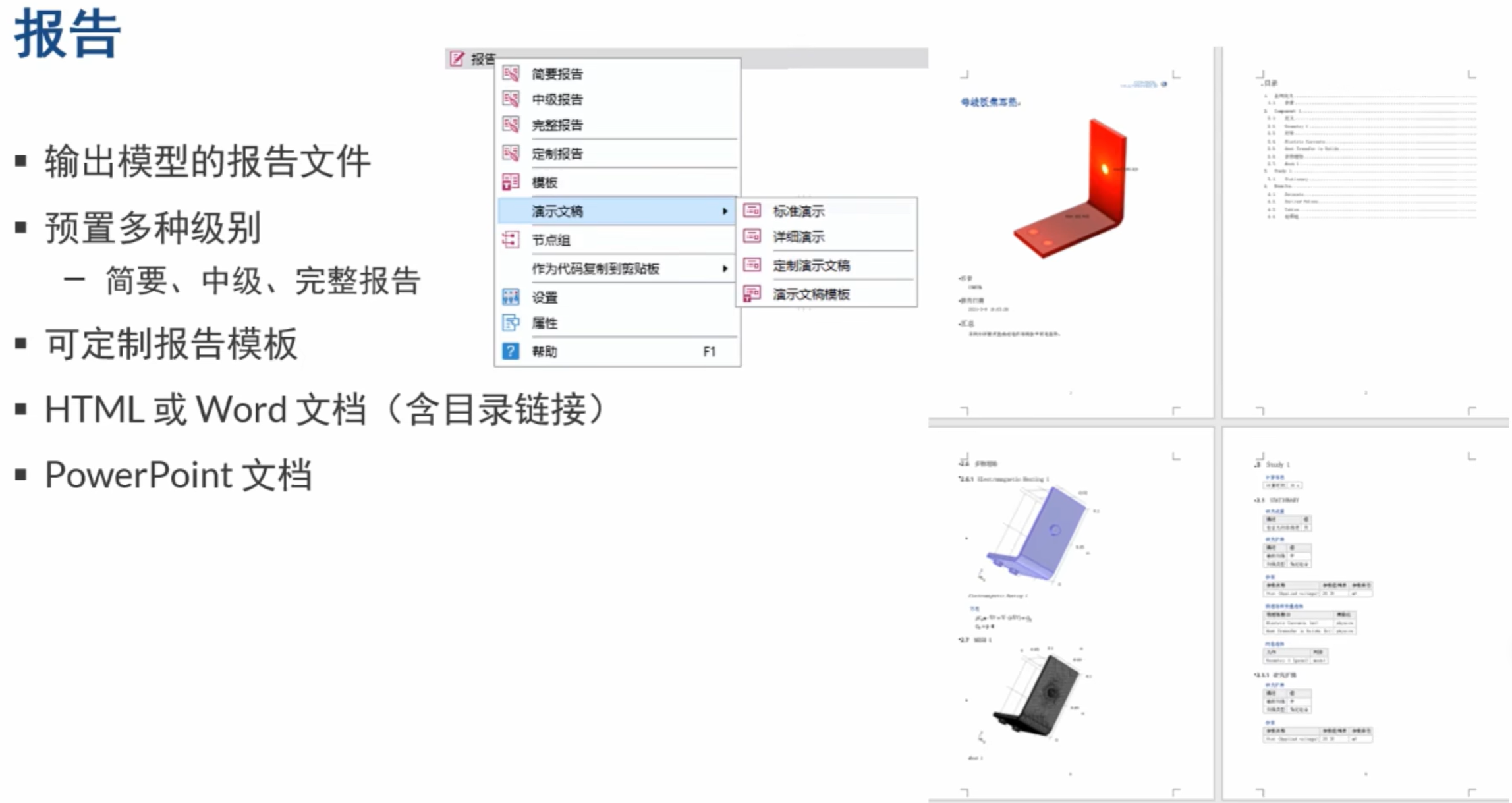
报告

寻找两条曲线的交点 —— root 函数

是一个数值求解工具，用于寻找单变量方程的根（即方程的解）。具体来说，它的作用是找到某个表达式在给定自变量范围内的零点（即满足表达式=0的变量值）。在寻找两条曲线的交点时，正是通过求取两条曲线的差值表达式的零点来实现的。

基本语法：

root(expr, var, initial_guess)

expr: 需要求解的表达式（必须是一个关于单变量var的方程）。

var: 自变量（如空间坐标x、时间t等）。

initial_guess: 对解的初始猜测值（需用户根据图形或物理意义预估）。

假设你需要找到两条曲线 \(y1(x)\) 和 \(y2(x)\) 的交点，数学上等价于求解方程：

\[y1(x) - y2(x) = 0 \]

此时，root 函数的作用是：

数值迭代：基于初始猜测值（initial_guess），通过迭代算法（如牛顿-拉夫森法）逼近方程的根。

返回结果：找到满足条件的自变量值 \(x_0\)，使得 \(y1(x_0) ≈ y2(x_0)\)。