COMSOL < 波动光学 > 学习笔记

COMSOL 模块介绍

什么是波动光学

1. 光频下的电磁波仿真
2. 光学元件经常大于波长
3. 只考虑波动性

电磁场模拟类型

官方“波动光学”使用手册

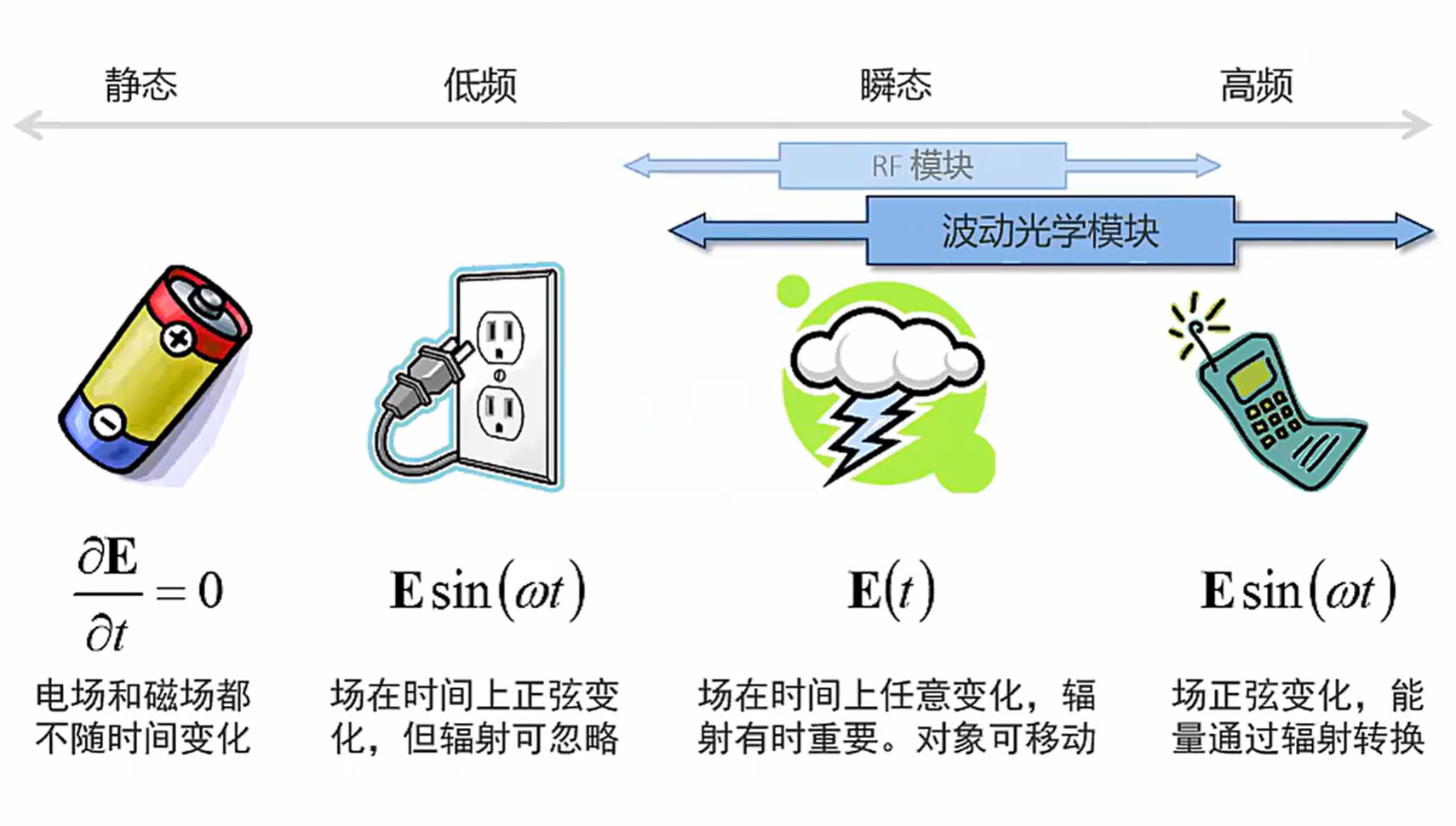
对比

RF 模块：适合模拟与波长大小相近的域
射线光学模块：用于模拟远大于波长的尺寸。波长近似为 0

应用

集成光学：波导和耦合器（类似集成电路）
光纤光学：光子晶体纤维、光纤 Bragg 光栅
非线性光学：谐波产生、和频与差频混合
光散射（ + 折射 / 反射）：表面散射、纳米颗粒散射
激光器和放大器：半导体激光器、棒 / 板和盘形激光器设计

例 1：金纳米球的光散射

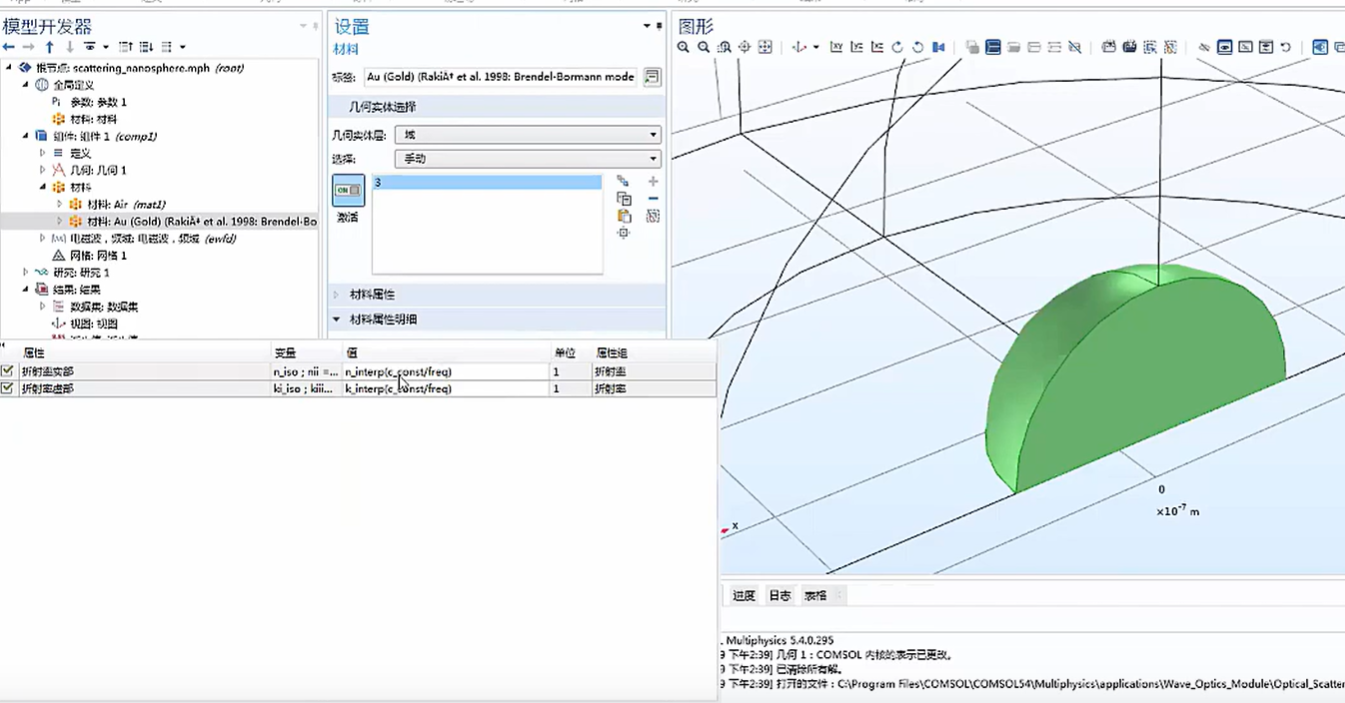
复值折射率：虚部为正代表材料有增益；虚部为负代表材料有损耗

图中 c_const 和 freq 为软件自带光速和频率。用 c_const / freq 表示函数自变量波长。

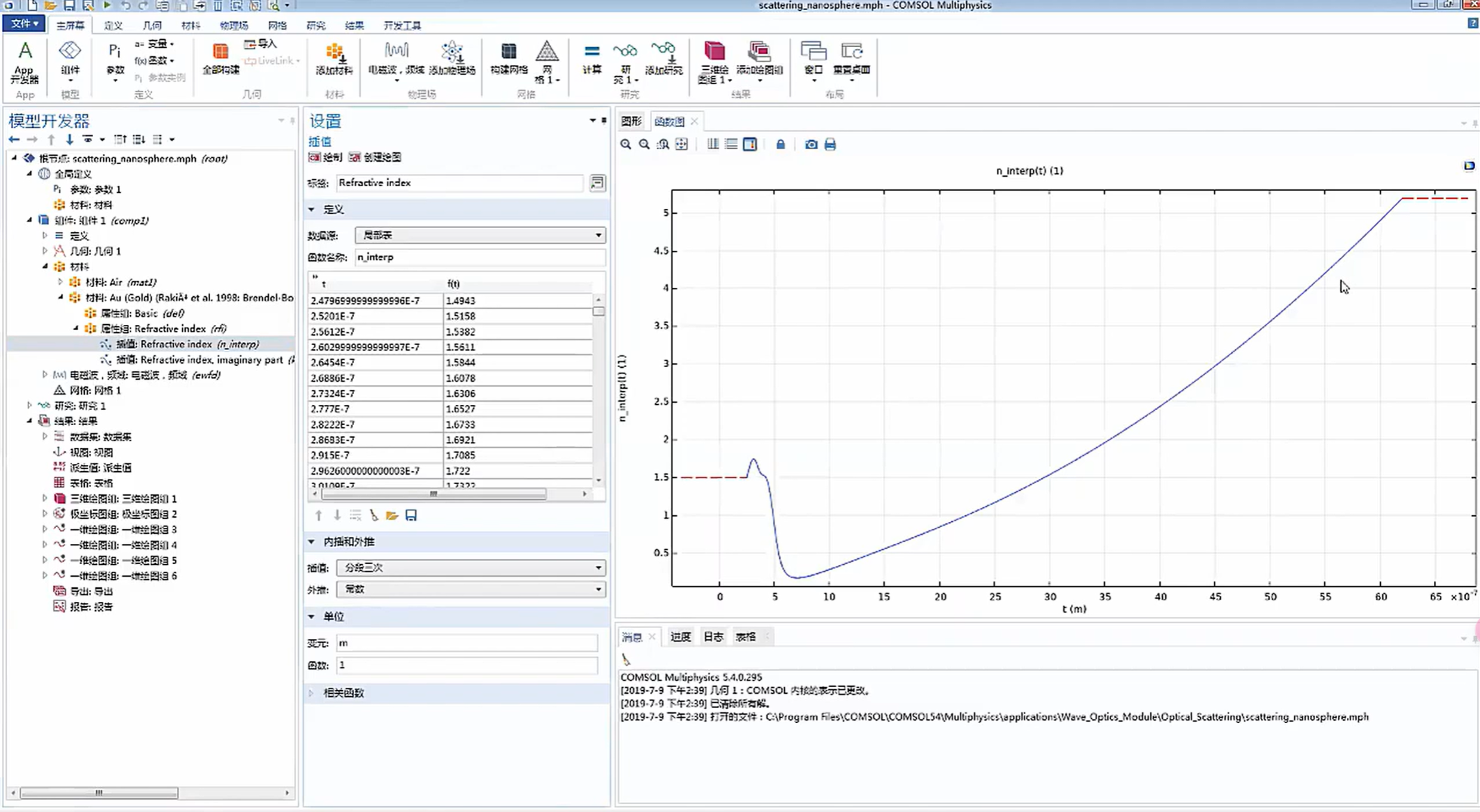
定义自变量取值和对应的函数取值。点击< 绘制 >可以查看函数图像。

波束包络法

参考视频

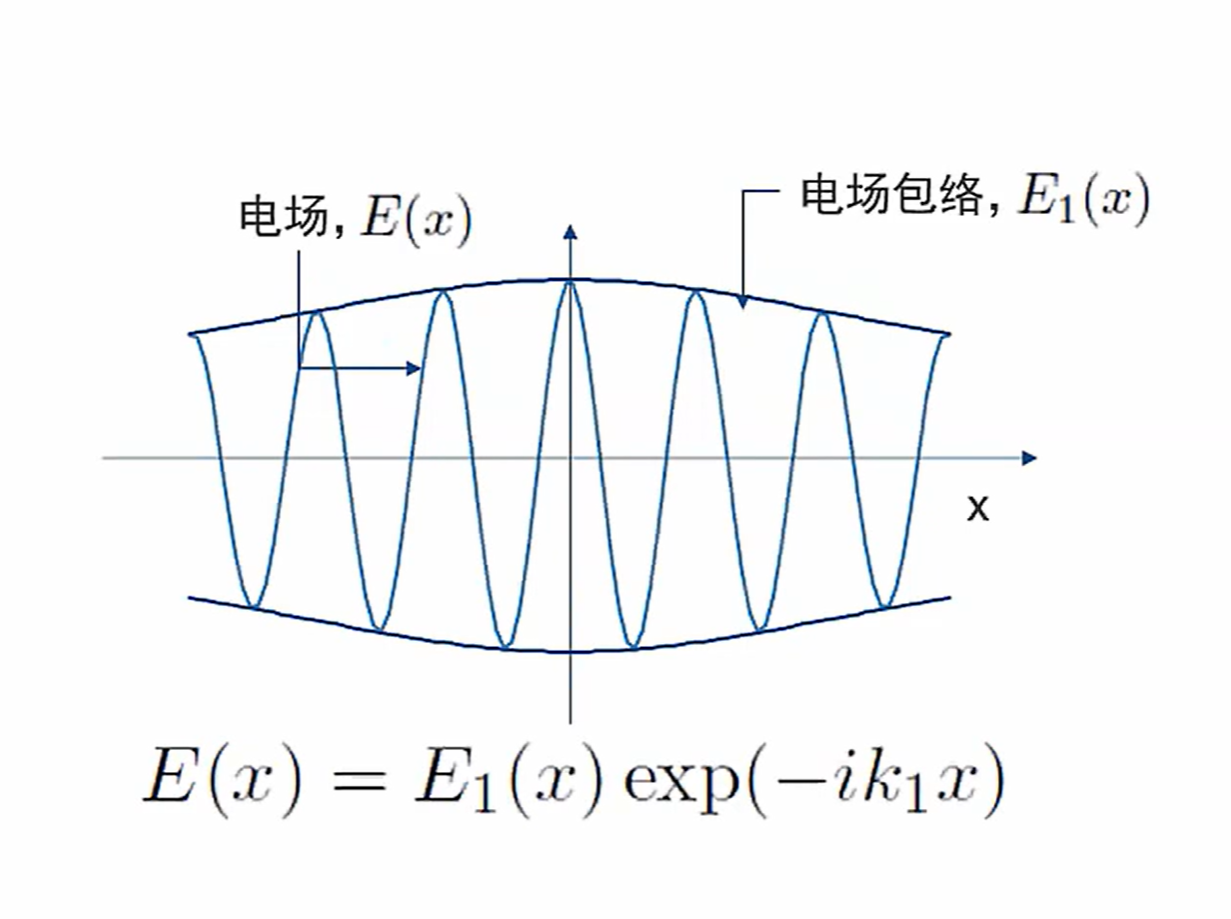
前提：必须知道波的传播方向 \(\vec{k}\)

波束包络法将 \(E\) 分解为载波（快速振荡项）和包络函数（缓慢变化项）的乘积：

\[\vec{E(x,y,z)}=\vec{E_{env}(x,y,z)}⋅e^{ −jβ⋅\vec{r}} \]

\(E_{env}\)：包络函数（缓慢变化，描述波束的幅度和相位分布）。

\(β\)：参考波矢，定义载波的传播方向和相位变化率。

\(\vec{r}\)：位置矢量。

波矢的定义方法：

\[β=k_0n \cdot \hat k = \frac{2πn}{λ_0} \cdot \hat k \]

设定初始值：

初始值即是对包络函数 \(E_{env}\) 的初始猜测，帮助求解器更快收敛到物理合理的解。

原理

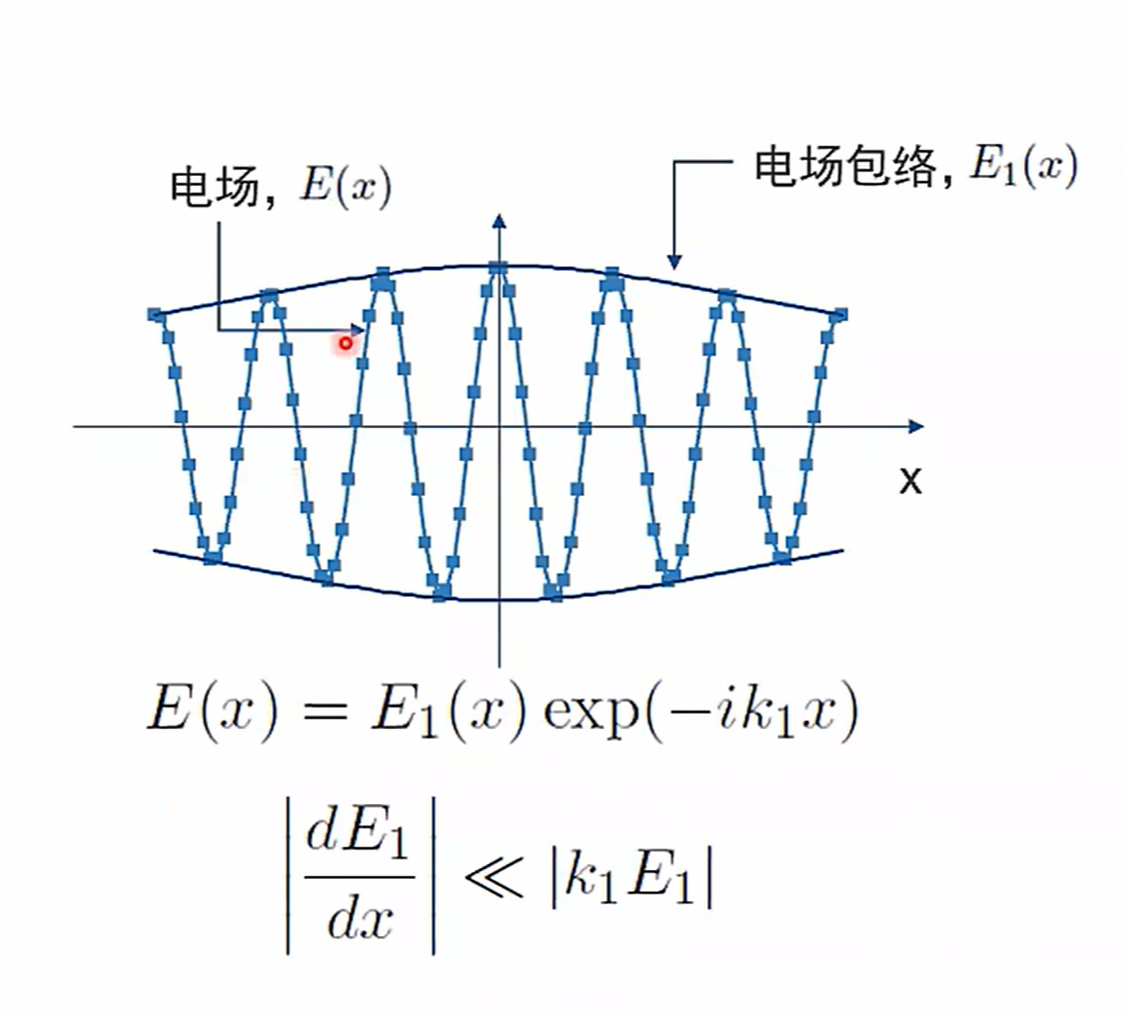
原始：电场每个波长至少需要剖分 5 个网格进行计算
包络线：波动性远低于原始电场。可以简化计算

适用范围

传输设定

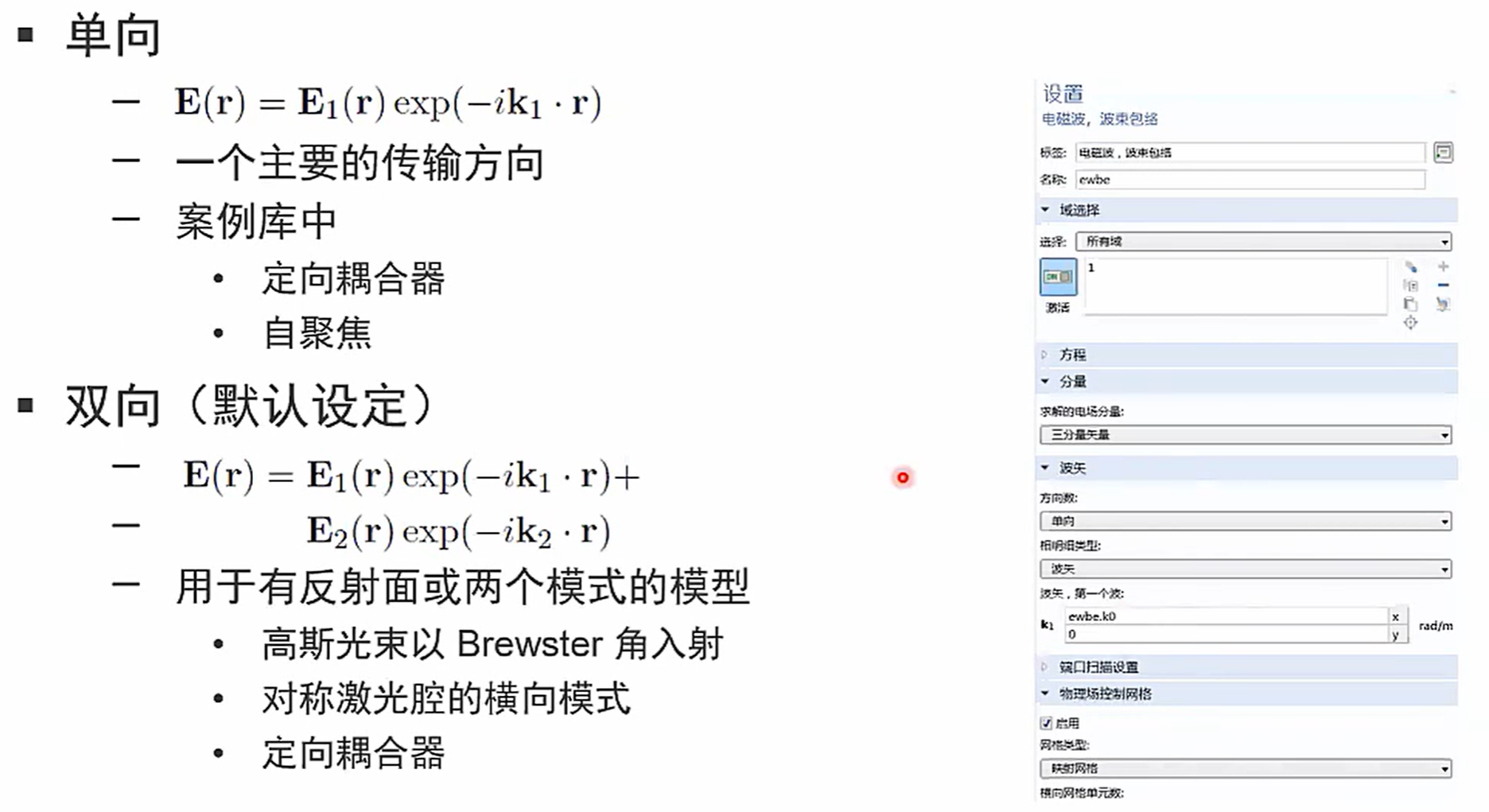
当已知相函数时，根据波矢是相函数的梯度，可以直接输入相函数来代替。

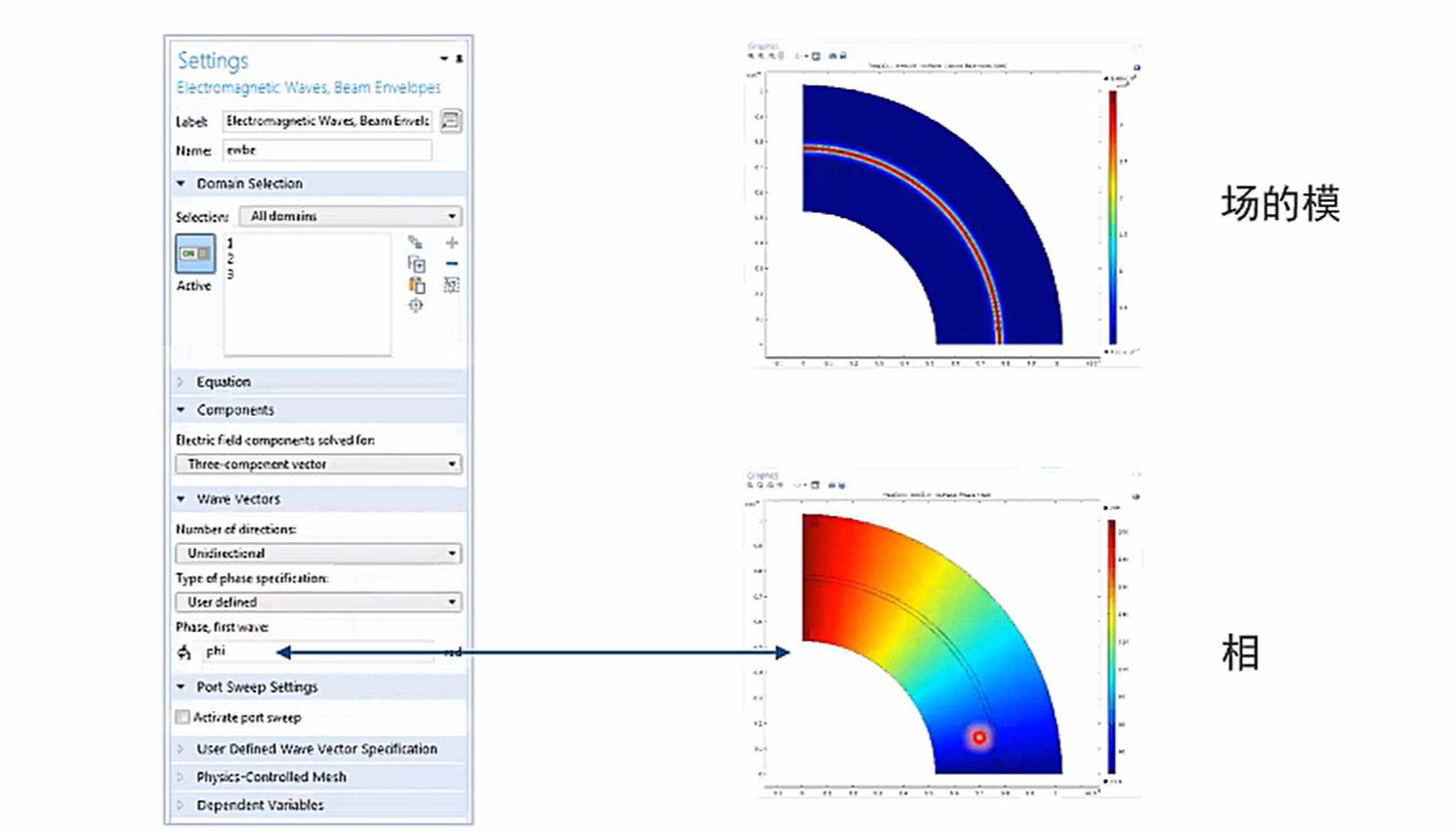
用户接口特征

边界条件

匹配边界条件

指定波的出射方向。可以用来消除波在边界上的反射。

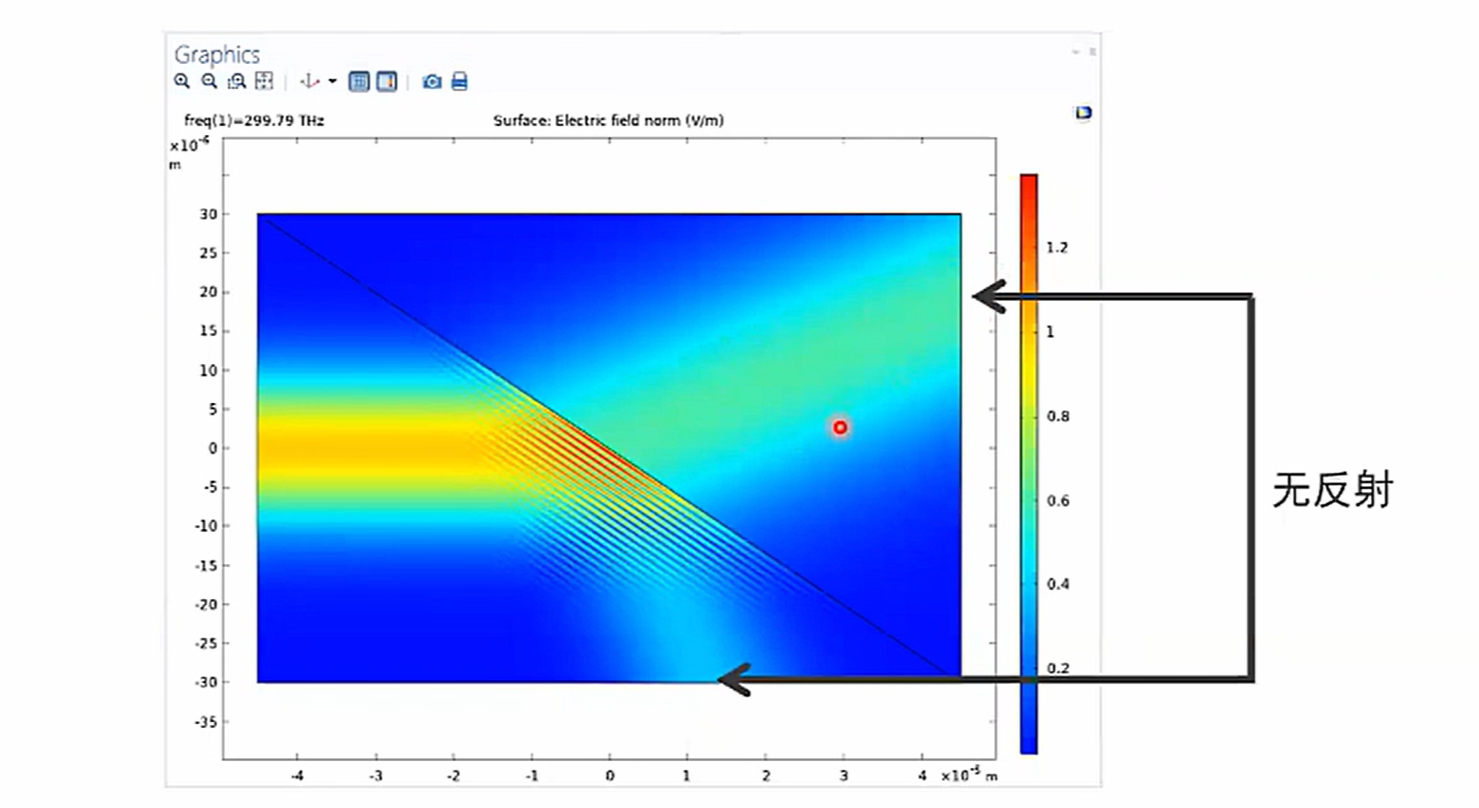
过渡边界条件

金属层的维度 = 模拟维度 - 1，可以减少计算量。可以指定金属层的厚度、色散系数等等。

阻抗边界条件

基底（白色部分）不参与网格剖分和计算，但可以用该边界条件模拟基底对光波的作用。

趋肤深度：描述高频电流或电磁波在导体中传播时的衰减特性。它表示电磁场（或电流）在导体内部的有效穿透深度，即场强衰减到表面值的约 \(37\%（1/e）\) 时的深度。
计算表达式：

\[δ = \sqrt{\frac{2}{ωμσ}} \]

趋肤深度越小，电流越集中在表面，导体内部的电流密度呈指数衰减。

在 COMSOL 电磁仿真中，当导体厚度远大于趋肤深度（\(t≫δ\)）时，可应用阻抗边界条件简化计算：

场连续性边界条件

适用于忽略相位变化的情况。

例 2：自聚焦光束

高斯光束：横截面的场强分布符合高斯函数，由中心向边缘衰减。

高斯光束可以导致材料属性变化，使中心折射率最高，引起光束向中心聚拢，抵消衍射效应（使光发散），形成自聚焦。

1.波矢的定义方法：

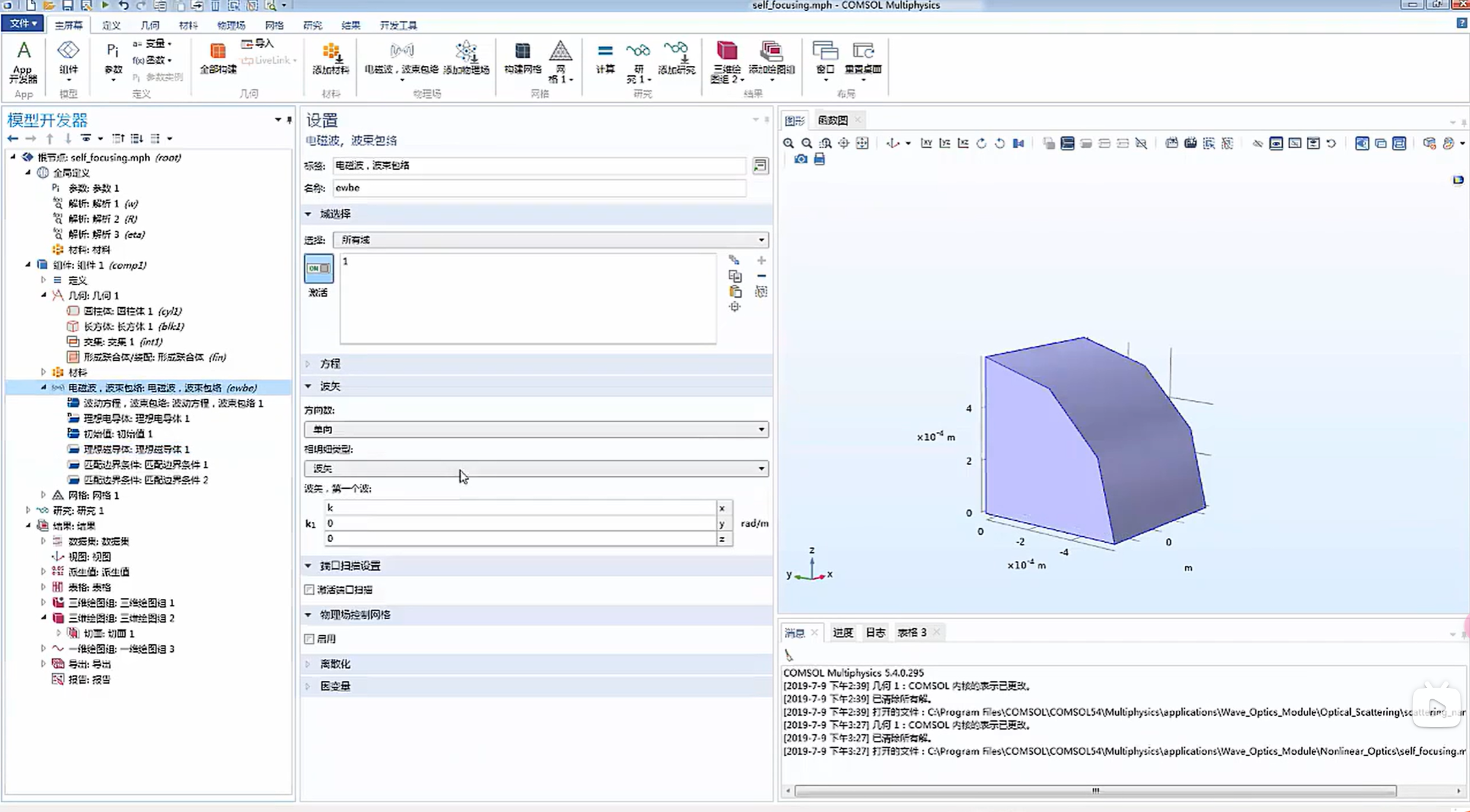
2.匹配边界条件可以用于定义入射波：

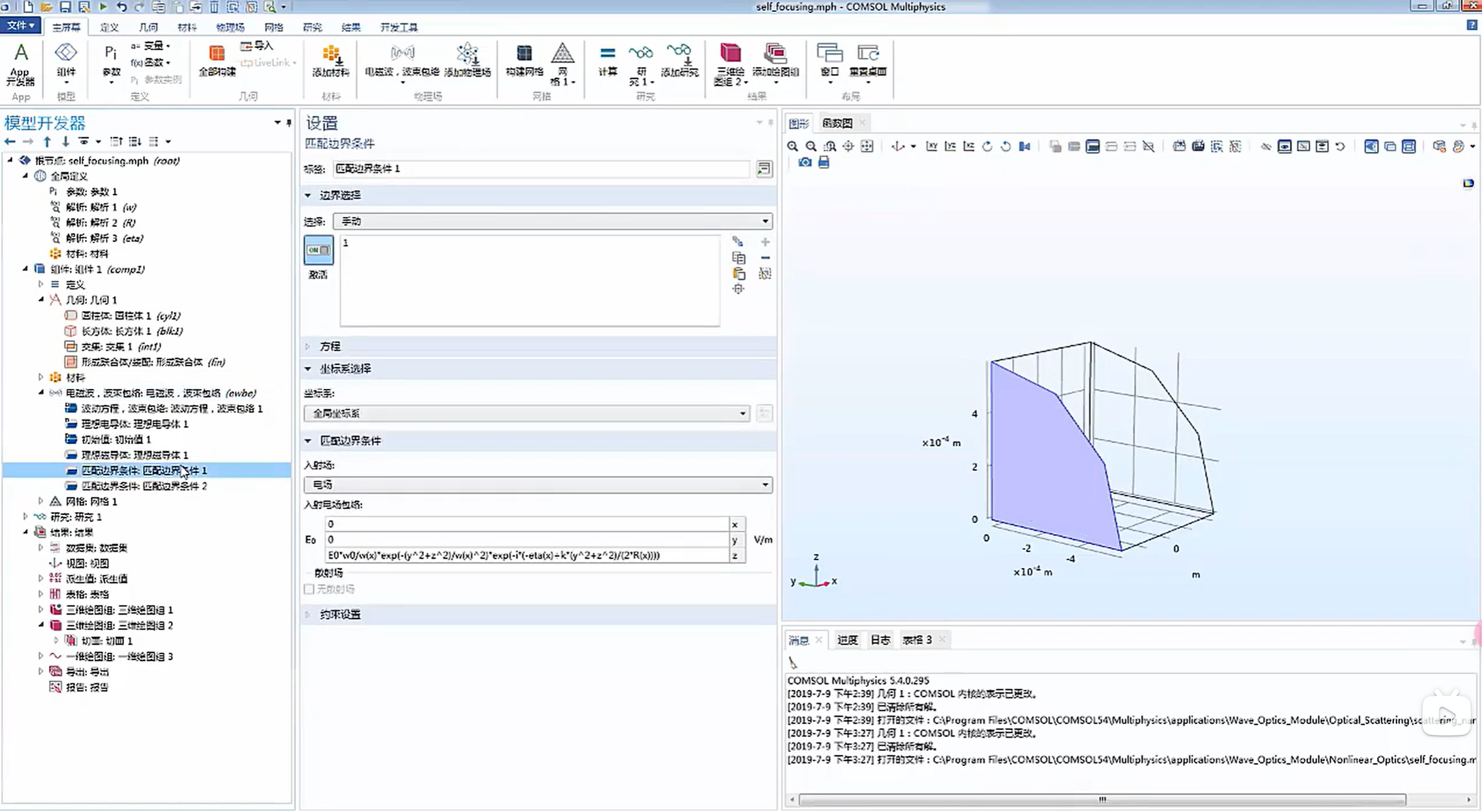
3.参数化扫描：

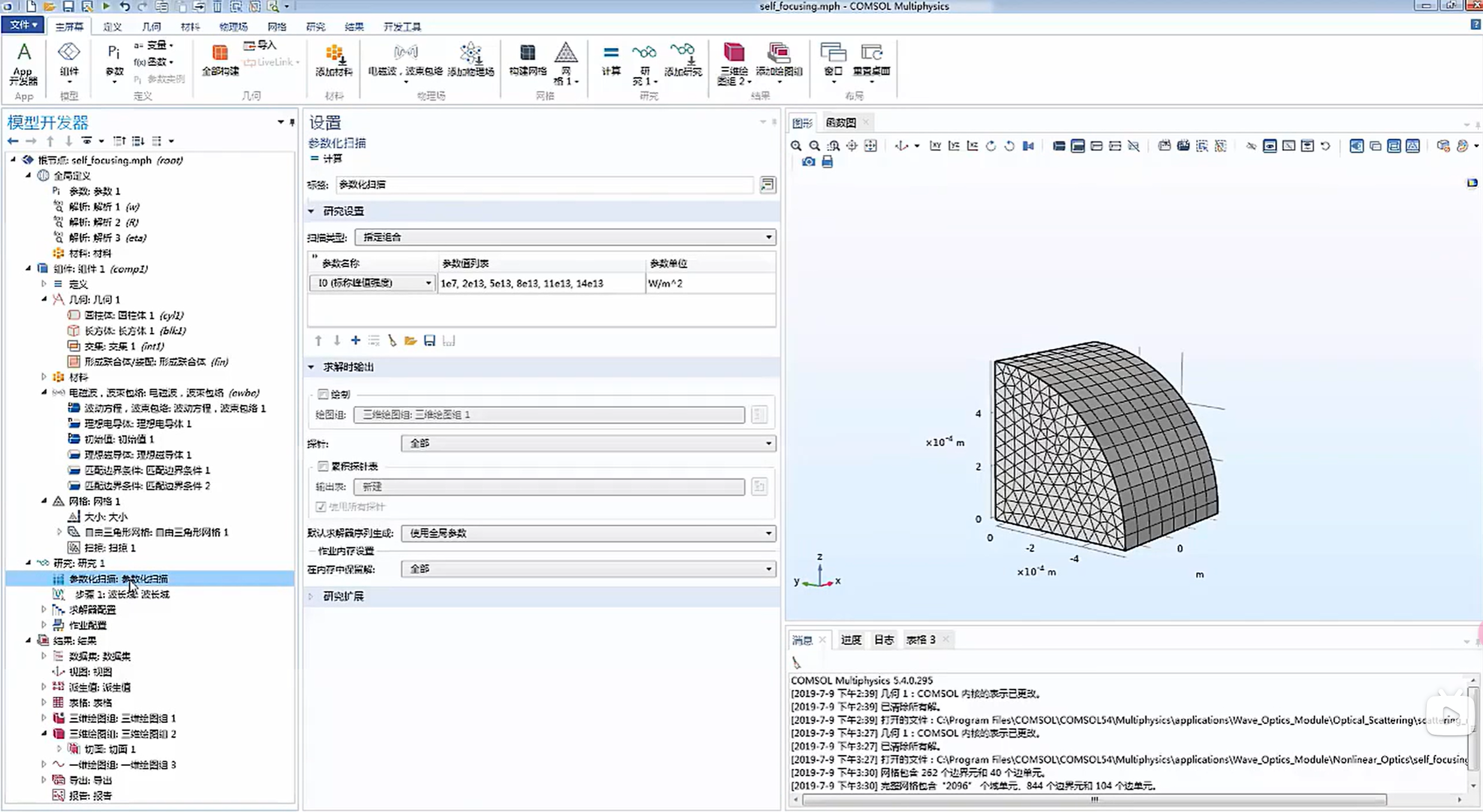
该案例对光强 I0 进行了扫描，指定了光强范围。求解时对不同的光强值分别进行求解。

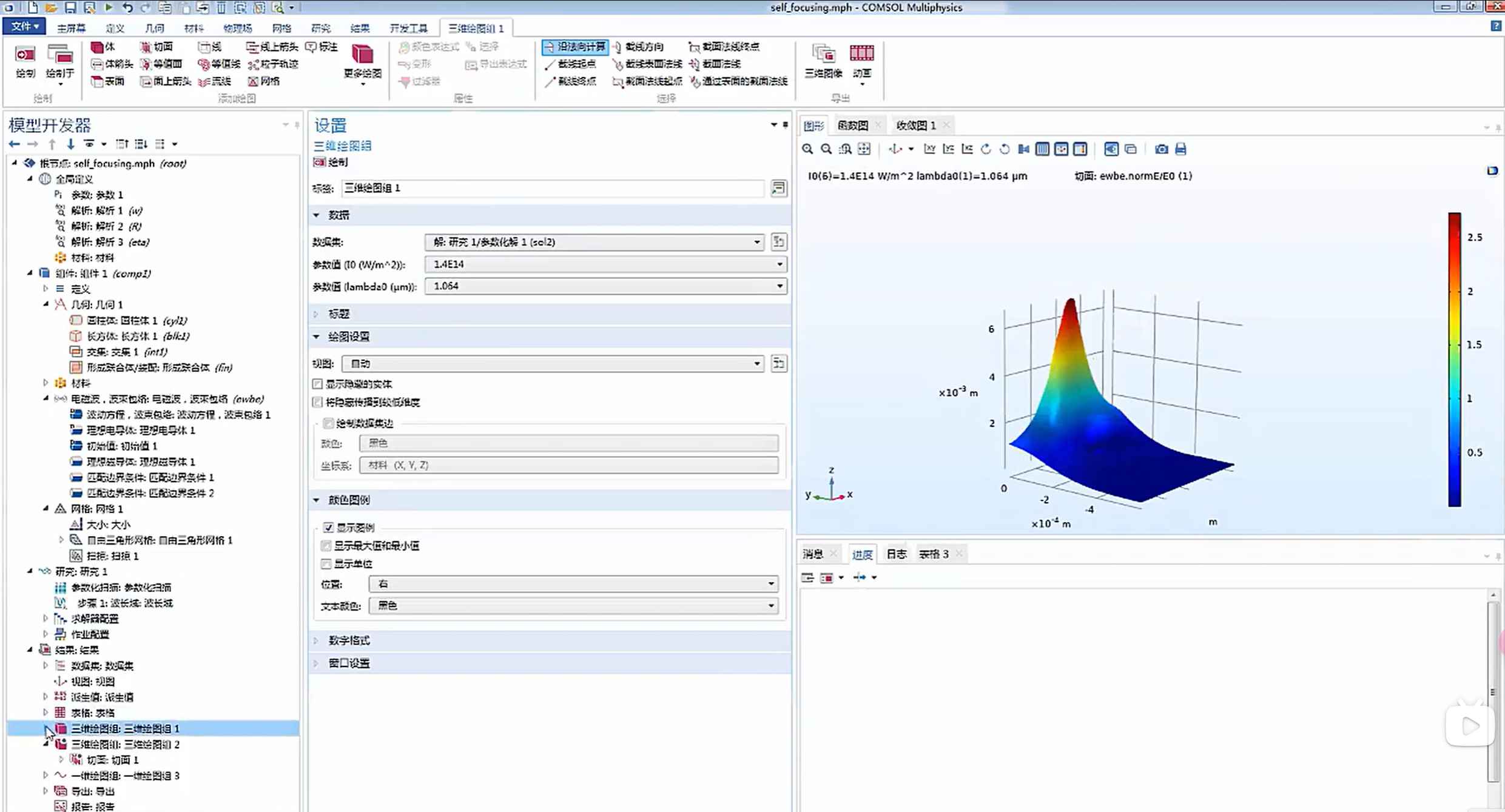
计算结束之后，可以选择查看不同参数值对应的结果。

周期性边界条件

1. 连续性：边界处两端幅度和相位一致

2. 反周期：边界处两端幅度一致、但相位差 180°

3. Floquet：产生相移。如果入射波波阵面平行边界，也即波矢量垂直边界，边界任意处波矢量相同，相移就是0，这时候Floquet周期边界就变成连续周期边界。

参考文章

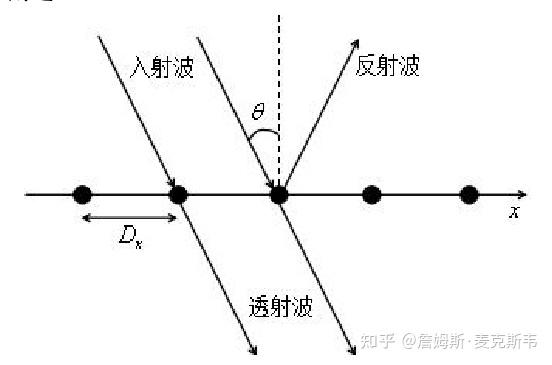
端口

以菲涅尔定律的反射和折射为例，周期性结构需要定义周期性端口。

输出端口的定义是必要的。从输入端口提取反射率，从输出端口提取透射率。

预设参数

变量名	物理意义	公式/说明
ewfd.normE	电场矢量的模（总电场强度）	\(\sqrt{{│E_x│}^2 + {│E_y│}^2 + {│E_z│}^2}\)
ewfd.normH	磁场矢量的模（总磁场强度）	\(\sqrt{{│H_x│}^2 + {│H_y│}^2 + {│H_z│}^2}\)
ewfd.Ex, ewfd.Ey, ewfd.Ez	电场的 x/y/z 分量（复数形式）	频域仿真中可分解为实部（_real）和虚部（_imag）
ewfd.Hx, ewfd.Hy, ewfd.Hz	磁场的 x/y/z 分量（复数形式）	同上
ewfd.Poavx, ewfd.Poavy, ewfd.Poavz	坡印廷矢量的时间平均功率流密度分量（W/m²）	\(\frac{1}{2} Re ( \vec{E} \times {\vec{H}}^* )\) 的 x/y/z 分量
ewfd.normPoav	坡印廷矢量的模（总功率流密度）	\(\sqrt{{│Poav_x│}^2 + {│Poav_y│}^2 + {│Poav_z│}^2}\)
ewfd.We	电场能量密度（J/m³）	\(\frac{1}{2} ε_0 ε_r {│\vec{E}│}^2\)
ewfd.Wm	磁场能量密度（J/m³）	\(\frac{1}{2} μ_0 μ_r {│\vec{H}│}^2\)
ewfd.Qh	焦耳热损耗密度（W/m³）	\(\frac{1}{2} σ {│\vec{E}│}^2\)（需材料电导率 \(σ\)）
ewfd.S11, ewfd.S21	散射参数（反射系数 \(S_{11}\) 和透射系数 \(S_{21}\)）	需在端口边界条件下启用
epsilonr_real	相对介电常数实部 （\(ε_{r_{real}}\)）
epsilonr_imag	相对介电常数虚部 （\(ε_{r_{imag}}\)，对应损耗）
mur	相对磁导率 （\(μ_r\)）
sigma	材料电导率 （\(σ\)）
ewfd.neff	模式有效折射率 （\(n_{eff} = \frac{β}{k₀}\)）
ewfd.beta	传播常数 （\(β = \frac{2π \times n_{eff}}{λ₀}\)）
freq	仿真频率 （\(f\)，单位 Hz）
lambda0	自由空间波长 （\(λ₀ = \frac{c₀}{f}\) ）

波束包络

变量名	物理意义	公式/说明
ewbe.k0	自由空间波数	\(2π / λ_0\)
ewbe.beta	参考波矢的模	\(2πn / λ_0\)
ewbe.n_eff	有效折射率	\(ewbe.beta / ewbe.k0\)
freq	用户定义的仿真频率	决定 ewbe.k0 的输入参数