做题记录4
4月1日
P1501 [国家集训队]Tree II(根号分治/CDQ分治)
P1501 [国家集训队]Tree II(根号分治/CDQ分治)
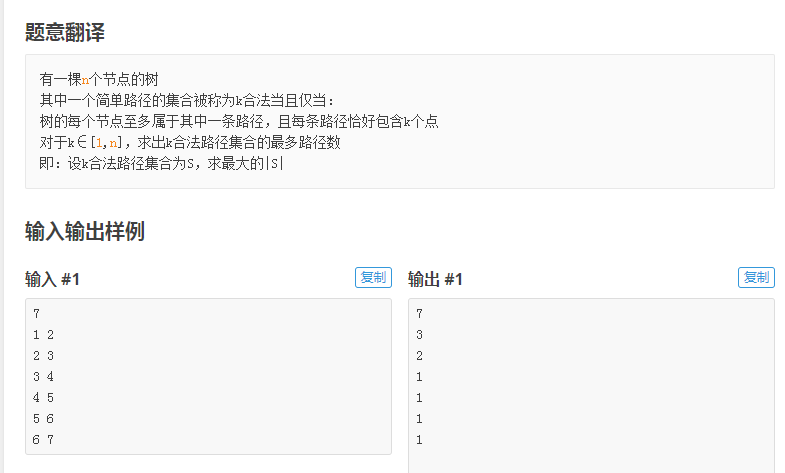
考虑根号分治。
首先对于 \(k<\sqrt{n}\) 的,我们直接每次暴力 \(O(n)\) dp 即可。
然后对于 \(\sqrt{n} \leq k\) 的,我们发现答案的种类只有 \(\sqrt{n}\) 级别,而且答案显然具有单调性,所以我们考虑对于每一个点二分其最右边的和它答案相同的点。
这样做是 \(O(nlogn\sqrt{n})\) 的,调整块长,变成 \(O(n\sqrt{nlogn})\) 。
同时也可以 \(cdq\) 分治,因为答案具有单调性,而这样做的时间复杂度似乎是 \(O(nlogn\sqrt{n})\) 的。
4月2日
P3703 [SDOI2017]树点涂色(LCT+线段树)
首先线段树区间染色,然后对于操作 1 很像 LCT 的 Access 操作,于是可以考虑 LCT 。
然后用线段树来维护 LCT 的信息即可。
当然也可以直接大力树剖,两个时间复杂度都是 \(O(nlog^2n)\) 。
CF1446D2 Frequency Problem (Hard Version)(根号分治)
CF1446D2 Frequency Problem (Hard Version)(根号分治)
首先这道题有一个结论:这两个元素当中一定有一个是众数,证明略。
那么考虑对于出现次数大于等于 \(\sqrt{n}\) 的数,我们可以把这些数枚举一下,然后这样做:
把值为当前数的位置标为 1 ,把值为众数的标为 -1 ,其他的都是 0 ,然后做一遍前缀和,记录每一个前缀和值的出现的最早的位置。
于是区间的长度那就是当前位置减掉这个前缀和第一次出现的位置(这样的话这个区间和就是 0)。
这部分的数的个数不超过 \(\sqrt{n}\) 个。
接下来是对于出现次数小于 $\sqrt{n} $的数。
我们可以枚举区间当中出现次数最多的数的次数,再枚举每一个 \(r\) ,求出最小的左端点 \(L_r\) ,整个过程是一个双指针。
可以参考这片题解
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5,T=505,INF=1e9+7;
int n,Maxn,cnt,Ans,S,val;
int a[N],Num[N],sum[N],t[N*2],cnt1[N],cnt2[N];
vector<int>v;
inline void Modify(int x,int v){cnt2[cnt1[x]]--,cnt1[x]+=v,cnt2[cnt1[x]]++;}
int main(){
read(n),S=sqrt(n);
for(int i=1;i<=n;i++) read(a[i]),Num[a[i]]++;
for(int i=1;i<=n;i++){
if(Num[i]==Maxn) cnt++;
if(Num[i]>Maxn) cnt=1,Maxn=Num[i];
}
if(cnt>1){write(n);return 0;}
for(int i=1;i<=n;i++){
if(Num[i]==Maxn) val=i;
else if(Num[i]>S) v.push_back(i);
}
for(int i=0;i<v.size();i++){
int k=v[i];
for(int j=1;j<=n;j++) sum[j]=sum[j-1]+(a[j]==k? -1:(a[j]==val? 1:0));
for(int j=-n;j<=n;j++) t[n+j]=INF;
for(int j=1;j<=n;j++) Ans=max(Ans,j-t[n+sum[j]]+1),t[n+sum[j-1]]=min(t[n+sum[j-1]],j);
}
for(int i=1;i<=S;i++){
for(int j=1;j<=n;j++) cnt1[j]=cnt2[j]=0;
int l=1,r=0;
while(r<n){
r++,Modify(a[r],1);
while(cnt1[a[r]]>i) Modify(a[l],-1),l++;
if(cnt2[i]>=2) Ans=max(Ans,r-l+1);
}
}
write(Ans);
return 0;
}
总结
这道题三个点,第一个是那个结论,第二个就是那个求区间和为 0 的区间,第三个是双指针。
P3396 哈希冲突(根号分治)
像这样的题大多可以考虑根号分治,也就是和模数有关的。
我们对于询问的值来分治:
对于小于 \(\sqrt{n}\) 的模数:
说明剩余系也不超过 \(\sqrt{n}\) 个,于是我们可以预处理这样的询问,需要时直接回答即可。
预处理时间复杂度是 \(O(n\sqrt{n})\) 的,询问 \(O(1)\)
对于大于等于 \(\sqrt{n}\) 的模数:
每个剩余系里面的元素不超过 \(\sqrt{n}\) 个。
于是对于每一个询问,我们可以直接枚举起点,然后不断地累加这个剩余系里面下标的答案即可。
这部分询问是 \(O(\sqrt{n})\) 的,时间复杂度是 \(O(m\sqrt{n})\) 。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5e4+5,M=405,INF=1e9+7;
int n,m,t,a[N];
int sum[M][M];//摸i时第j个池子的情况
int main(){
read(n),read(m);t=sqrt(n);
for(int i=1;i<=n;i++) read(a[i]);
for(int i=1;i<=t;i++) for(int j=1;j<=n;j++) sum[i][j%i]+=a[j];
for(int i=1,x,y;i<=m;i++){
char op[5];
scanf("%s",op);read(x),read(y);
if(op[0]=='A'){
if(x<=t) write(sum[x][y]),putchar('\n');
else{
int Sum=0;
for(int j=y;j<=n;j+=x) Sum+=a[j];
write(Sum),putchar('\n');
}
}
else{
for(int j=1;j<=t;j++) sum[j][x%j]-=a[x];
for(int j=1;j<=t;j++) sum[j][x%j]+=y;
a[x]=y;
}
}
return 0;
}
CF103D Time to Raid Cowavans(根号分治)
CF103D Time to Raid Cowavans(根号分治)
这一道题和上一道题 哈希冲突很像,多了的就是这里要预处理的是前缀和,这样空间开不下。
所以这样来做:

然后空间复杂度降至 \(O(n)\),可以通过。
P5901 [IOI2009]regions(根号分治)

代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define ll long long
#define PII pair<int,int>
const int N=2e5+5,M=25005;
int head[N],nex[N],a[N],Ans[N];
vector<PII> v1[M],v2[M];
inline void Add(int u,int v){nex[v]=head[u],head[u]=v;}
int sum1[N],sum2[N];
void DFS(int x){
for(int i=0,l=v2[a[x]].size();i<l;i++) Ans[v2[a[x]][i].second]+=sum2[v2[a[x]][i].first];
sum1[a[x]]++,sum2[a[x]]++;
for(int i=0,l=v1[a[x]].size();i<l;i++) Ans[v1[a[x]][i].second]-=sum1[v1[a[x]][i].first];
for(int v=head[x];v;v=nex[v]) DFS(v);
for(int i=0,l=v1[a[x]].size();i<l;i++) Ans[v1[a[x]][i].second]+=sum1[v1[a[x]][i].first];
sum2[a[x]]--;
return ;
}
map<PII,int>f;
int n,R,Q,siz,pos[N],cnt[M];
int main(){
read(n),read(R),read(Q),siz=sqrt(n);
read(a[1]),cnt[a[1]]++;
for(int i=2,x,y;i<=n;i++) read(x),read(y),Add(x,i),a[i]=y,cnt[y]++;
for(int i=1,r1,r2;i<=Q;i++){
map<PII,int>::iterator it;
read(r1),read(r2);
if((it=f.find(make_pair(r1,r2)))==f.end()){
f[make_pair(r1,r2)]=pos[i]=i;
if(cnt[r2]<=siz) v2[r2].push_back(make_pair(r1,i));
else v1[r1].push_back(make_pair(r2,i));
}
else pos[i]=it->second;
}
DFS(1);
for(int i=1;i<=Q;i++) write(Ans[pos[i]]),putchar('\n');
return 0;
}
注意
这道题值得学习的是对于每个点求祖先贡献的那一步。
4月3日
P5064 [Ynoi2014] 等这场战争结束之后(值域分块+并查集)
P5064 [Ynoi2014] 等这场战争结束之后(值域分块+并查集)
建出操作树,离散化,然后并查集+值域分块维护。

代码:
#include<bits/stdc++.h>
#define PII pair<int,int>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5,M=36;
int n,m,a[N],fa[N],siz[N],B,t=2778,id[N],RES[N],head[N],idx,top;
short int s[N][M+2];
struct edge{int v,nex;}e[N];
struct opt{int op,x,y;}p[N];
int Getfa(int x){if(x==fa[x])return x;return Getfa(fa[x]);}
PII stk[N];
void Merge(int x,int y){
x=Getfa(x),y=Getfa(y);
if(x==y) return ;
if(siz[x]<siz[y]) swap(x,y);
fa[y]=x,siz[x]+=siz[y];
for(int now=0;now<=B;now++) s[x][now]+=s[y][now];
stk[++top]=make_pair(x,y);
return ;
}
void Delete(int p){
while(p--){
PII x=stk[top--];siz[x.first]-=siz[x.second],fa[x.second]=x.second;
for(int now=0;now<=B;now++) s[x.first][now]-=s[x.second][now];
}
return ;
}
int Query(int x,int y){
x=Getfa(x);
if(y>siz[x]) return -1;
int pos=0;
while(s[x][pos]<y){
y-=s[x][pos];
pos++;
}
for(int now=0;now<t;now++){
if(Getfa(id[pos*t+now])==x) y--;
if(y==0) return a[id[pos*t+now]];
}
}
void Add(int u,int v){e[++idx].v=v;e[idx].nex=head[u];head[u]=idx;}
bool cmp(int x,int y){return a[x]<a[y];}
void Dfs(int x){
int Top=top;
if(p[x].op==1) Merge(p[x].x,p[x].y);
else if(p[x].op==3){RES[x]=Query(p[x].x,p[x].y);}
for(int now=head[x];now;now=e[now].nex){int y=e[now].v;Dfs(y);}
if(p[x].op==1){int len=top-Top;Delete(len);}
}
int main(){
read(n),read(m);
B=(n/t)+1;
for(int now=1;now<=n;now++) read(a[now]),id[now]=now;
sort(id+1,id+n+1,cmp);
for(int now=1;now<=n;now++) fa[now]=now,s[id[now]][(now/t)]=siz[now]=1;
for(int now=1;now<=m;now++){
read(p[now].op),read(p[now].x);
if(p[now].op==2) Add(p[now].x,now);
else read(p[now].y),Add(now-1,now);
}
Dfs(0);
for(int now=1;now<=m;now++) if(p[now].op==3) write(RES[now]),putchar('\n');
return 0;
}
P4692 [Ynoi2016] 谁的梦(set+思想)
首先正难则反是必须想到的,我们可以考虑先不管所有的值,把全部值都作为答案统计一边,然后减去贡献即可。
重点在于怎么减去贡献,容易发现,我们这样做其实就是把每个序列分成了很多段,于是我们考虑用 set 维护每一个断点的前驱后继,然后暴力算答案即可。
注意有一个坑点是 0 没用逆元,必须特判。
时间复杂度 \(O(nlogn)\) 。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define int long long
const int N=2e5+5,MOD=19260817;
int n,m,len[N],tot2,res,sum1[N],sum2[N],Cnt[N],tot,Sum;
vector<int>p[N];
map<int,int> Map;
map<pair<int,int>,int> Map2;
set<int>st[N*5];
set<int>::iterator it,IT;
int QuickPow(int x,int y,int res=1){for(;y;y>>=1,x=x*x%MOD)if(y&1)res=res*x%MOD;return res;}
int Getpos(int x){if(Map.find(x)==Map.end())sum1[Map[x]=++tot]=Sum;return Map[x];}
int GetPos(int x,int y) {
if(Map2.find(make_pair(x,y))==Map2.end()){
st[Map2[make_pair(x,y)]=++tot2].insert(0),st[tot2].insert(len[y]+1);
sum2[tot2]=(len[y]*(len[y]+1)>>1)%MOD;
}
return Map2[make_pair(x,y)];
}
void Insert(int c,int x,int now){
res-=Sum-((!Cnt[c])?sum1[c]:0);
if(!sum2[x]) Cnt[c]--;
else sum1[c]=sum1[c]*QuickPow(sum2[x],MOD-2)%MOD;
it=st[x].lower_bound(now),IT=--it,++it;
sum2[x]=(sum2[x]-((*it-*IT)*(*it-*IT-1)>>1))%MOD;
sum2[x]=(sum2[x]+((now-*IT)*(now-*IT-1)>>1))%MOD;
sum2[x]=(sum2[x]+((*it-now)*(*it-now-1)>>1)+MOD)%MOD;
if(!sum2[x])++Cnt[c];
else sum1[c]=sum1[c]*sum2[x]%MOD;
res+=Sum-((!Cnt[c])?sum1[c]:0),st[x].insert(now);
return ;
}
void Delete(int c,int x,int now){
res-=Sum-((!Cnt[c])?sum1[c]:0);
if(!sum2[x]) Cnt[c]--;
else sum1[c]=sum1[c]*QuickPow(sum2[x],MOD-2)%MOD;
st[x].erase(now),it=st[x].lower_bound(now),IT=--it,++it;
sum2[x]=(sum2[x]-((now-*IT)*(now-*IT-1)>>1))%MOD;
sum2[x]=(sum2[x]-((*it-now)*(*it-now-1)>>1))%MOD;
sum2[x]=(sum2[x]+((*it-*IT)*(*it-*IT-1)>>1)+MOD+MOD)%MOD;
if(!sum2[x]) Cnt[c]++;
else sum1[c]=sum1[c]*sum2[x]%MOD;
res+=Sum-((!Cnt[c])?sum1[c]:0);
return ;
}
signed main() {
read(n),read(m),Sum=1;
for(int i=1;i<=n;i++) read(len[i]),Sum=(len[i]*(len[i]+1)>>1)%MOD*Sum%MOD,p[i].resize(len[i]+2);
for(int i=1;i<=n;i++) for(int j=1;j<=len[i];j++) read(p[i][j]);
for(int i=1;i<=n;i++) for(int j=1;j<=len[i];j++) Insert(Getpos(p[i][j]),GetPos(p[i][j],i),j);
res=(res%MOD+MOD)%MOD;
write(res),putchar('\n');
for(int i=1,x,y,z;i<=m;i++){
read(x),read(y),read(z);
Delete(Getpos(p[x][y]),GetPos(p[x][y],x),y),p[x][y]=z;
Insert(Getpos(p[x][y]),GetPos(p[x][y],x),y);
res=(res%MOD+MOD)%MOD;
write(res),putchar('\n');
}
return 0;
}
LOJ517「LibreOJ β Round #2」计算几何瞎暴力
LOJ517「LibreOJ β Round #2」计算几何瞎暴力
要求维护一个全局异或,动态在末尾加元素,询问区间和,全局排序的数据结构。
首先因为是全局异或,这个可以想到直接打标记,然后在末尾加元素可以用一个缓存数组,重点在于全局排序还要区间询问和该怎么办。
根据排序,可以想到 \(Trie\) 来做,同时区间和其实就是对应 \(Trie\) 树上的一段,再加之全局异或标记,其实就是树上 0/1 路径的交换。
所以对于已经排好序的存到 \(Trie\) 里,剩下的搞一个数组缓存并随时维护前缀和即可。
然后区间和就是相当于在 \(Trie\) 里询问再加上一段前缀和,可以用类似 \(Trie\) 树上二分的操作来实现。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e6+5;
int a[N],pos,n,m;
int pre[N][31],ls[N<<1],rs[N<<1],bit[N<<1][31],siz[N<<1],num[N<<1],cnt=1,x,tmpx,dx;
void ins(int k){
++siz[1];
for(int j=0,p=1;j<=30;j++,p<<=1) bit[1][j]+=((k&p)>0);
for(int i=30,t=1<<30,id=1;i>=0;i--,t>>=1){
if(k&t){
if(!rs[id]) rs[id]=++cnt,num[cnt]=num[id]+t;
id=rs[id];
}
else{
if(!ls[id]) ls[id]=++cnt,num[cnt]=num[id];
id=ls[id];
}
for(int j=0,p=1;j<=30;j++,p<<=1) bit[id][j]+=((k&p)>0);
++siz[id];
}
return ;
}
long long GetNum(int t,int k,int id){
if(!k||!id) return 0;
if(k==siz[id]){
long long res=0;
for(int j=0,p=1;j<=30;j++,p<<=1) res+=1ll*p*((p&x)?(k-bit[id][j]):bit[id][j]);
return res;
}
if(t==0){return 1ll*k*(num[id]^x);}
if(dx&t)if(k<=siz[rs[id]]) return GetNum(t>>1,k,rs[id]); else return GetNum(t>>1,siz[rs[id]],rs[id])+GetNum(t>>1,k-siz[rs[id]],ls[id]);
else if(k<=siz[ls[id]]) return GetNum(t>>1,k,ls[id]); else return GetNum(t>>1,siz[ls[id]],ls[id])+GetNum(t>>1,k-siz[ls[id]],rs[id]);
}
signed main(){
read(n);
for(int i=1;i<=n;i++){
read(a[i]);
for(int j=0,p=1;j<=30;j++,p<<=1) pre[i][j]=pre[i-1][j]+((a[i]&p)>0);
}
read(m);int op,k;
while(m--){
read(op);
if(op==1){
read(k);
a[++n]=k^x;
for(int j=0,p=1;j<=30;j++,p<<=1) pre[n][j]=pre[n-1][j]+((a[n]&p)>0);
}
else if(op==3){
int g;read(g);
x^=g,tmpx^=g;
}
else if(op==4){
while(pos<n) ins(a[++pos]);
dx^=tmpx,tmpx=0;
}
else{
int l,r;read(l),read(r);
long long res;
if(r<=pos){
res=GetNum(1<<30,r,1)-GetNum(1<<30,l-1,1);
write(res),putchar('\n');
}
else if(l>pos){
res=0;
for(int j=0,p=1;j<=30;j++,p<<=1) res+=1ll*p*((p&x)?(r-l+1-pre[r][j]+pre[l-1][j]):(pre[r][j]-pre[l-1][j]));
write(res),putchar('\n');
}
else{
res=GetNum(1<<30,pos,1)-GetNum(1<<30,l-1,1);
for(int j=0,p=1;j<=30;j++,p<<=1) res+=1ll*p*((p&x)?(r-pos-pre[r][j]+pre[pos][j]):(pre[r][j]-pre[pos][j]));
write(res),putchar('\n');
}
}
}
return 0;
}
P3645 [APIO2015]雅加达的摩天楼(BFS+根号平衡)
P3645 [APIO2015]雅加达的摩天楼(BFS+根号平衡)
牛逼题,根本不用最短路,直接分析得出:
对于跳跃能力小于 \(\sqrt{n}\) 的,可行的状态只有 \(O(n\sqrt{n})\) 个。
对于跳跃能力大于 \(\sqrt{n}\) 的,最多跳 \(\sqrt{n}\) 次,所以可行的状态只有 \(O(m\sqrt{n})\) 个。
所以直接 \(BFS\) 一遍再判重即可,时间复杂度 \(O(n\sqrt{n})\) ,用 \(Map\) 会 T 。
Map代码:
#include<bits/stdc++.h>
#define PII pair<int,int>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;bool f=false;char ch=getchar();
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5,M=105;
int n,m,dis[N],S,T;
bool vis[N];
struct node{
int b,p,step;
node(int b=0,int p=0,int step=0):b(b),p(p),step(step){}
};
map<PII,int> Map;
queue<node> q;
vector<int> vec[N];
void BFS(){
for(int i=0;i<vec[S].size();i++) q.push(node(S,vec[S][i],0)),Map[make_pair(S,vec[S][i])]=1;
while(!q.empty()){
node t=q.front();q.pop();
int pos=t.b,x=t.p,step=t.step;
if(dis[T]!=-1) break;
int w1=pos-x;
if(!Map[make_pair(w1,x)]||(w1>=0&&!vis[w1])){
if(w1>=0){
if(!vis[w1]){
vis[w1]=true;
for(int i=0;i<vec[w1].size();i++) q.push(node(w1,vec[w1][i],step+1)),Map[make_pair(w1,vec[w1][i])]=1;
}
q.push(node(w1,x,step+1));Map[make_pair(w1,x)]=1,dis[w1]=step+1;
}
}
int w2=pos+x;
if(!Map[make_pair(w2,x)]||(w2<n&&!vis[w2])){
if(w2>=n) continue;
if(!vis[w2]){
vis[w2]=true;
for(int i=0;i<vec[w2].size();i++) q.push(node(w2,vec[w2][i],step+1)),Map[make_pair(w2,vec[w2][i])]=1;
}
q.push(node(w2,x,step+1));Map[make_pair(w2,x)]=1,dis[w2]=step+1;
}
}
}
int main(){
read(n),read(m);
int u,v;read(u),read(v);q.push(node(u,v,0));S=u;
read(u),read(v);T=u;dis[T]=-1;vec[u].push_back(v);
for(int i=3;i<=m;i++) read(u),read(v),vec[u].push_back(v);
if(S==T){write(0);return 0;}
Map[make_pair(u,v)]=1;vis[S]=true,dis[S]=0;
BFS();
write(dis[T]);
return 0;
}
4月4日
BS4150【NOI2014模拟17】花园(树剖,线段树,差分)
BS4150【NOI2014模拟17】花园(树剖,线段树,差分)
这道题可以差分然后线段树询问来做,同时也可以直接树剖然后在线段树内部用 set 维护。
可知线段树树高严格 \(logn\) ,所以单次修改是 \(O(log^3n)\) ,查询是 \(O(log^2n)\) ,1e5的数据比较卡,可以用差分的思路变成 2log 。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)) f|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
}
const int N=1e6+5;
#define ll long long
int n,m,root;
int head[N],nex[N],to[N],idx,val[N];
int dep[N],siz[N],son[N],fa[N],dfn[N],top[N],rev[N],tot;
multiset<int>S[N<<2];
void Add(int u,int v){
nex[++idx]=head[u];
to[idx]=v;
head[u]=idx;
return ;
}
void Dfs1(int x,int f){
siz[x]=1,fa[x]=f,dep[x]=dep[f]+1;
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(y==f) continue;
Dfs1(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
return ;
}
void Dfs2(int x){
if(x==son[fa[x]]) top[x]=top[fa[x]];
else top[x]=x;
dfn[x]=++tot;rev[tot]=x;
if(son[x]) Dfs2(son[x]);
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(y==fa[x]||y==son[x]) continue;
Dfs2(y);
}
return ;
}
int sum[N<<2];
void Pushup(int x){
multiset<int>::iterator it;
for(it=S[x<<1].begin();it!=S[x<<1].end();it++) S[x].insert(*it);
for(it=S[x<<1|1].begin();it!=S[x<<1|1].end();it++) S[x].insert(*it);
sum[x]=S[x].size();
return ;
}
void Update(int x,int lose,int get){
if(lose==get) return ;
while(floor(x>>1)>0){
int f=floor(x>>1);
S[f].erase(S[f].find(lose));
S[f].insert(get);
x=f;
}
return ;
}
void Build(int x,int l,int r){
if(l==r){S[x].insert(val[rev[l]]);return ;}
int mid=l+r>>1;
Build(x<<1,l,mid),Build(x<<1|1,mid+1,r);
Pushup(x);
return ;
}
void Modify(int x,int l,int r,int ql,int qr,int k){
if(ql<=l&&qr>=r){
Update(x,*S[x].begin(),k);
S[x].erase(*S[x].begin());S[x].insert(k);
sum[x]=1;
return ;
}
int mid=l+r>>1;
if(ql<=mid) Modify(x<<1,l,mid,ql,qr,k);
if(qr>mid) Modify(x<<1|1,mid+1,r,ql,qr,k);
return ;
}
int Query(int x,int l,int r,int ql,int qr,int k){
if(ql<=l&&qr>=r){return S[x].count(k);}
int mid=l+r>>1;int res=0;
if(ql<=mid) res+=Query(x<<1,l,mid,ql,qr,k);
if(qr>mid) res+=Query(x<<1|1,mid+1,r,ql,qr,k);
return res;
}
void RoadModify(int x,int y,int k){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
Modify(1,1,n,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
Modify(1,1,n,dfn[y],dfn[x],k);
return ;
}
ll RoadQuery(int x,int y,int k){
ll res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res+=Query(1,1,n,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
res+=Query(1,1,n,dfn[y],dfn[x],k);
return res;
}
int QueryLCA(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
return y;
}
int main(){
//freopen("tree.in","r",stdin);
//freopen("tree.out","w",stdout);
read(n),read(m);
for(int i=1;i<=n;i++) read(val[i]);
for(int i=1;i<n;i++){
int u,v;
read(u),read(v);
Add(u,v),Add(v,u);
}
root=1;
Dfs1(1,0);
Dfs2(1);
Build(1,1,n);
for(int i=1,x,y,k,las=0;i<=m;i++){
char op[4];
scanf("%s",op);
if(op[0]=='C'){
read(x),read(k);
x^=las,k^=las;
Modify(1,1,n,dfn[x],dfn[x],k);
}
else{
read(x),read(y),read(k);
x^=las,k^=las,y^=las;
las=RoadQuery(x,y,k);
write(las),putchar('\n');
}
}
return 0;
}
差分代码:
#include<bits/stdc++.h>
using namespace std;
#define l(x) t[x].l
#define r(x) t[x].r
#define a(x) t[x].add
#define v(x) t[x].val
const int N=1e5+5;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)) f|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
}
struct Segment_Tree{int l,r,add,val;}t[N*100];
map<int,int> val;
int n,q,ans,sum,size,T[N],root[N<<2];
int tot,top,head[N],to[N<<1],nex[N<<1],dep[N],fa[N][20],dfn[N<<1],b[N],e[N];
void add(int u,int v){nex[++tot]=head[u],head[u]=tot,to[tot]=v;}
void dfs(int x){
dfn[++top]=x;
for(int i=1;i<=16;i++){
if((1<<i)<=dep[x]) fa[x][i]=fa[fa[x][i-1]][i-1];
else break;
}
for(int i=head[x];i;i=nex[i]) if(to[i]!=fa[x][0]) fa[to[i]][0]=x,dep[to[i]]=dep[x]+1,dfs(to[i]);
dfn[++top]=x;
}
int QueryLca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
int temp=dep[u]-dep[v];
for(int i=0;i<=16;i++) if(temp&(1<<i)) u=fa[u][i];
for(int i=16;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return u==v?u:fa[u][0];
}
void PushDown(int p,int l,int r){
if(!a(p)||l==r) return;
int temp=a(p);
if(!l(p)) l(p)=++size;
if(!r(p)) r(p)=++size;
a(p)=0,v(l(p))+=temp,a(l(p))+=temp,v(r(p))+=temp,a(r(p))+=temp;
}
void Modify(int &p,int l,int r,int x,int y,int d){
if(!p) p=++size;
PushDown(p,l,r);
if(x==l&&y==r){v(p)+=d,a(p)+=d;return;}
int mid=(l+r)>>1;
if(x<=mid) Modify(l(p),l,mid,x,min(y,mid),d);
if(y>mid) Modify(r(p),mid+1,r,max(x,mid+1),y,d);
}
int Query(int p,int l,int r,int x){
if(!p) return 0;
PushDown(p,l,r);
if(l==r) return v(p);
int mid=(l+r)>>1;
if(x<=mid) return Query(l(p),l,mid,x);
else return Query(r(p),mid+1,r,x);
}
int main(){
read(n),read(q);
for(int i=1;i<=n;i++){
read(T[i]);
if(!val[T[i]]) val[T[i]]=++sum;
T[i]=val[T[i]];
}
for(int i=1,u,v;i<n;i++) read(u),read(v),add(u,v),add(v,u);
dfs(1);
for(int i=1;i<=top;i++){
if(!b[dfn[i]]) b[dfn[i]]=i;
else e[dfn[i]]=i;
}
for(int i=1;i<=n;i++) Modify(root[T[i]],1,top,b[i],e[i],1);
for(int i=1,x,y,z;i<=q;i++){
char op[3];
scanf("%s",op),read(x),read(y),x^=ans,y^=ans;
if(op[0]=='Q'){
read(z),z^=ans;
int Lca=QueryLca(x,y);
if(!val[z]){ans=0,puts("0");continue;}
z=val[z],ans=Query(root[z],1,top,b[x])+Query(root[z],1,top,b[y])-2*Query(root[z],1,top,b[Lca]);
if(T[Lca]==z) ans++;
write(ans),putchar('\n');
}
if(op[0]=='C'){
if(!val[y]) val[y]=++sum;
y=val[y],Modify(root[T[x]],1,top,b[x],e[x],-1),Modify(root[y],1,top,b[x],e[x],1),T[x]=y;
}
}
}
4月5日
CF1503C Travelling Salesman Problem(贪心,势能分析)
CF1503C Travelling Salesman Problem(贪心,势能分析)
首先,每个城市的 \(c_i\) 可以看作是必花的代价。
然后我们考虑对城市进行势能分析:如果海拔增高,势能增加,海拔降低,势能不变。
于是我们考虑额外代价:如果前 \(i\) 个数的 \(a_i+c_i\) 的最大值小于 \(a_{i+1}\) ,那么我们就要扩大势能,变成 \(a_{i+1}\) 。
最后的答案就是本来的加上扩大的额外代价。
代码如下:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5;
int n;
long long ans;
struct node{
int a,c;
bool operator<(const node B)const{return a<B.a;}
}a[N];
int main(){
read(n);
for(int i=1;i<=n;i++) read(a[i].a),read(a[i].c),ans+=a[i].c;
sort(a+1,a+n+1);
int cur=0;
for(int i=1;i<=n;i++){
cur=max(cur,a[i].a+a[i].c);
if(cur<a[i+1].a) ans+=a[i+1].a-cur;
}
write(ans);
return 0;
}
P7479 【B】至曾是英雄的您(模拟,连通块)
其实可以围的条件就是:黑棋最多一个“真眼”。
于是考虑什么情况下一个联通块空地成为一个“真眼”:即不存在至少这样的一个点满足其四面都没有黑棋。
那么判断一下再染色,最后看有多少个连通块没有被染色即可。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e3+5;
int n,m,T,x[6]={0,1,-1,0,0},y[6]={0,0,0,-1,1},num[N][N],tot;
char s[N][N];
bool vis[N][N];
inline bool Check(int X,int Y){return (X>=1&&Y>=1&&X<=n&&Y<=m);}
inline bool CheckPut(int X,int Y){
for(int i=1;i<=4;i++) if(num[X+x[i]][Y+y[i]]!=1) return false;
return true;
}
void dfs(int nx,int ny){
vis[nx][ny]=true;
for(int i=1;i<=4;i++){
int fx=nx+x[i],fy=ny+y[i];
if(!Check(fx,fy)) continue;
if(!vis[fx][fy]) dfs(fx,fy);
}
return ;
}
int main(){
read(T);
while(T--){
read(n),read(m);
tot=0;
for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
for(int i=0;i<=n+1;i++){
for(int j=0;j<=m+1;j++){
num[i][j]=1;vis[i][j]=false;
if(s[i][j]=='*') num[i][j]=0,vis[i][j]=true;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(s[i][j]!='*'){
if(vis[i][j]) continue;
if(CheckPut(i,j)) dfs(i,j);
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(!vis[i][j]) tot++,dfs(i,j);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
s[i][j]=' ';
}
}
if(tot<=1) puts("NO");
else puts("YES");
}
return 0;
}
P7480 【C】Reboot from Blue(最短路,李超树优化dp)
P7480 【C】Reboot from Blue(最短路,李超树优化dp)
首先,我们发现,直接建图跑最短路肯定不行,因为这样做会有 \(O(n^2)\) 条边。
那么我们可以考虑减少无用的边。
有这样一个性质:对于一个点,我们发现它只会取到离它左最近或者右最近的比当前点油费小的点。
这是为什么呢?因为相当于如果我们走到这个左端点或者右端点的时候,我们无论是向左还是向右,我们都有更好的选择:在那一个油站加油,再去往下一个目的地。
同样的,为什么是比当前点油价小呢,显而易见,这是因为如果某个地方比当前点油价还要高,那我们还不如就用当前点的油了。
也就是说,这样的话我们只需要把每一个点对于左边和右边各一个点连边即可,这样边数的级别就变成 \(O(n)\) 了。
最后我们再给终点新建一个对应的结点,跑一遍从 \(s\) 对应点到 \(t\) 对应点的最短路即可。
时间复杂度 \(O(nlogn)\) 。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define ll long long
const int N=2e6+5;
const ll INF=2e18+5;
int n,hh=1,tt=0,sta[N],dp[N];
struct node{
ll val;int pos,id;
}a[N];
inline bool cmp(node x,node y){return x.pos<y.pos;}
int head[N],nex[N<<1],to[N<<1],idx,s,t;
ll val[N<<1],dis[N];
bool vis[N];
void add(int u,int v,ll w){
nex[++idx]=head[u];
to[idx]=v;
head[u]=idx;
val[idx]=w;
return ;
}
#define PII pair<ll,int>
priority_queue<PII,vector<PII>,greater<PII> >q;
void dijkstra(){
for(int i=1;i<=n;i++) dis[i]=INF;
dis[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
PII t=q.top();q.pop();
int x=t.second;ll dist=t.first;
if(vis[x]) continue;
vis[x]=true;
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(dist+val[i]<dis[y]){
dis[y]=dist+val[i];
q.push(make_pair(dis[y],y));
}
}
}
return ;
}
signed main(){
read(n),read(s),read(t);
for(int i=1;i<=n;i++) read(a[i].val),read(a[i].pos),a[i].id=i;
sort(a+1,a+n+1,cmp);
for(int i=n;i>=1;i--){
while(hh<=tt&&a[i].val<=a[sta[tt]].val) --tt;
dp[i]=sta[tt];
sta[++tt]=i;
}
for(int i=1;i<=n;i++) if(dp[i]) add(i,dp[i],abs(a[i].pos-a[dp[i]].pos)*a[i].val);
tt=0,hh=1;
for(int i=1;i<=n;i++){
while(hh<=tt&&a[i].val<=a[sta[tt]].val) --tt;
dp[i]=sta[tt];
sta[++tt]=i;
}
for(int i=1;i<=n;i++) if(dp[i]) add(i,dp[i],abs(a[i].pos-a[dp[i]].pos)*a[i].val);
for(int i=1;i<=n;i++) if(a[i].pos==s){s=i;break;}
n++;
for(int i=1;i<n;i++) add(i,n,abs(t-a[i].pos)*a[i].val);
dijkstra();
write(dis[n]);
return 0;
}
P4289 [HAOI2008]移动玩具(搜索,BFS)
发现状态数量非常少,于是考虑直接搜索,然后就是一个状压判重之类的即可。
代码:
#include<bits/stdc++.h>
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
char ch[6];
int s,t,q[N],hh,tt,d[N];
int f[4]={-4,+1,+4,-1};
void read(int&x){for(int i=0;i<4;i++){scanf("%s",ch);for(int j=0;j<4;j++) if(ch[j]-'0') x+=1<<(i*4+j);}}
void bfs(){
q[tt++]=s,d[s]=1;
int now,nd,tmp;
while(hh<tt){
now=q[hh++],nd=d[now]+1;
for(int i=0;i<16;i++)
if(now&(1<<i)){
for(int j=0;j<4;j++){
if(j==0&&i/4==0) continue;
if(j==1&&i%4==3) continue;
if(j==2&&i/4==3) continue;
if(j==3&&i%4==0) continue;
tmp=i+f[j];
if(now&(1<<tmp)) continue;
tmp=now^(1<<i)^(1<<tmp);
if(nd<d[tmp]) d[tmp]=nd,q[tt++]=tmp;
if(tmp==t) return;
}
}
}
return ;
}
int main(){
read(s),read(t);
memset(d,0x7f,sizeof(d));
bfs();
write(d[t]-1);
return 0;
}
P2512 [HAOI2008]糖果传递(贪心,数学)
把式子写出来再稍微改写一下就变成了经典的多个绝对值求最小值。
结论显而易见就是选最中间的一段区间。
具体就是:

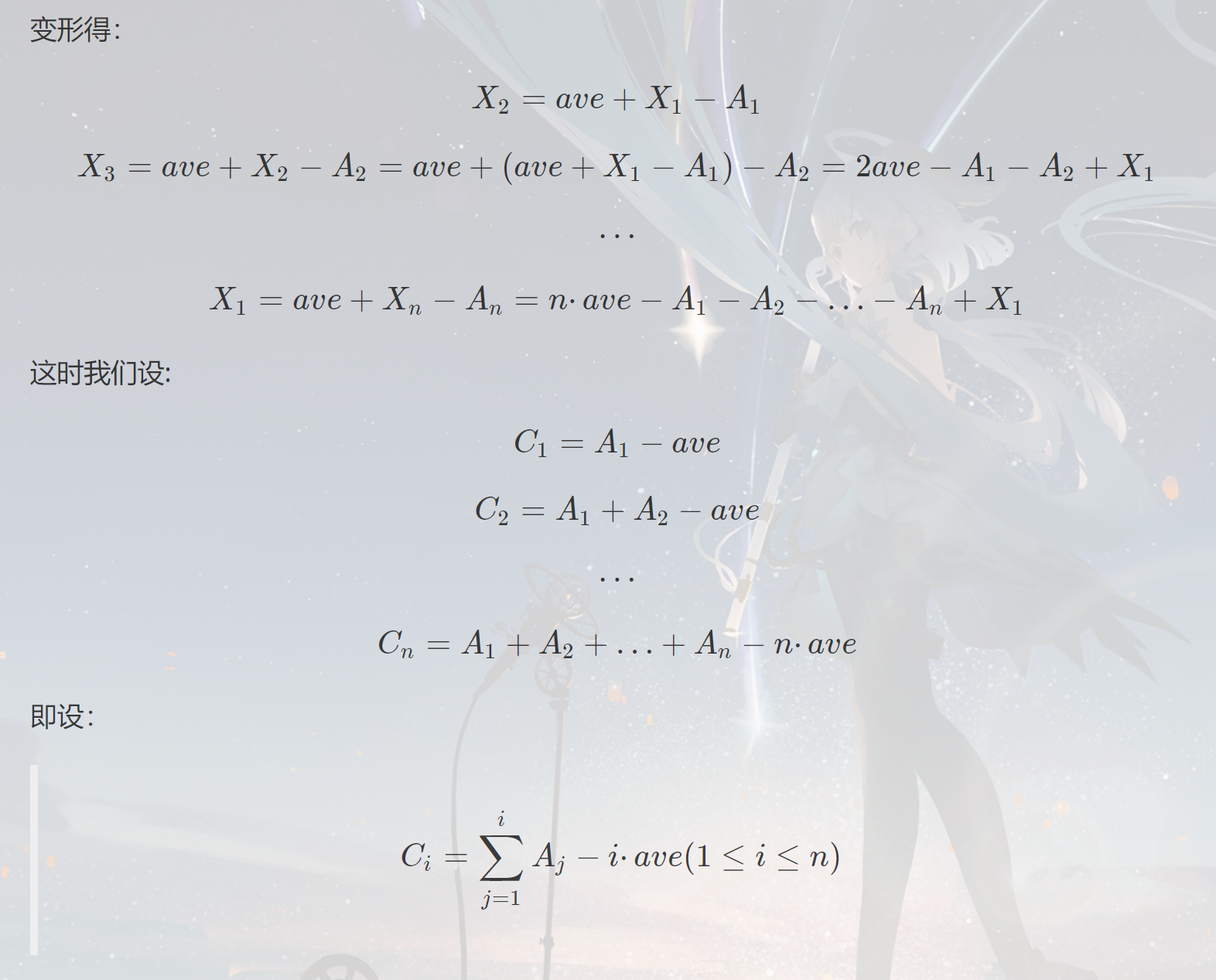


代码:
#include<bits/stdc++.h>
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e6+5;
#define ll long long
ll n,a[N],c[N],ave,ans,mid;
using namespace std;
int main(){
read(n);
for(int i=1;i<=n;i++) read(a[i]),ave+=a[i];ave/=n;
for(int i=1;i<=n;i++) c[i]=c[i-1]+ave-a[i-1];sort(c+1,c+n+1);mid=c[(n+1)/2];
for(int i=1;i<=n;i++) ans+=abs(mid-c[i]);
write(ans);
return 0;
}
P2511 [HAOI2008]木棍分割(前缀和优化dp+二分)
P2511 [HAOI2008]木棍分割(前缀和优化dp+二分)
首先第一问是明显的二分答案。
然后考虑第二问怎么做。
主要就是转移比较烦,但是发现这个式子可以前缀和优化一下,然后滚动数组就可以转移了。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define inc(x,y) (x+y>=MOD?x+y-MOD:(x+y<0?x+y+MOD:x+y))
const int N=5e4+5,MOD=10007;
int n,m,L[N],pre[N],f[N],g[N],pos[N],F[N],G[N];
bool check(int x){
int res=0,tot=1;
for(int i=1;i<=n;i++){
if(L[i]>x) return false;
if(res+L[i]>x) tot++,res=L[i];
else res+=L[i];
}
return tot<=m+1;
}
int main(){
read(n),read(m);
for(int i=1;i<=n;i++) read(L[i]),pre[i]=pre[i-1]+L[i];
int l=1,r=pre[n],mid;
while(l<r){
mid=(l+r)>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
for(int i=1;i<=n;i++){
int ll=1,rr=i-1,midd,anss=-1;
while(ll<rr){
midd=(ll+rr)>>1;
if(pre[i]-pre[midd]<=l) rr=midd;
else ll=midd+1,anss=midd+1;
}
pos[i]=(anss==-1?0:anss);
//for(int k=i-1;pre[i]-pre[k]<=l&&k>=0;k--) pos[i]=k;
}
F[0]=1;int ans=0;
for(int i=0;i<=n;i++) G[i]=1;
for(int j=1;j<=m+1;j++){
for(int i=0;i<=n;i++){
f[i]=inc(G[i-1],-(!pos[i]?0:G[pos[i]-1]));
g[i]=inc(g[i-1],f[i]);
}
for(int i=0;i<=n;i++) F[i]=f[i],G[i]=g[i],f[i]=g[i]=0;
ans=inc(ans,F[n]);
}
write(l),putchar(' '),write(inc(ans,MOD));
return 0;
}
P2597 [ZJOI2012]灾难(支配树)
DAG 上的支配树模板题。
支配的意思和这里的灭绝完全一样,具体来说就是:如果当前这个点被消除了,那么这个点子树内的所有点都消除。
具体来看怎么建出来这个支配树:
首先建出反图,跑一遍拓扑序,然后每次遍历到一个点,其在支配树上的结点的父亲就是其原图所有出边的点在树上的 LCA 。
然后就很好做了,直接用倍增 LCA 来维护这个支配树,然后再询问子树 \(siz\) 减一即可。
注意 0 的处理。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
int head[N],nex[N],to[N],idx;
int fa[N][22],dep[N],inv[N],ans[N];
int n,m,len,t;
vector<int> vec[N],st[N];
void add(int u,int v){
nex[++idx]=head[u];
to[idx]=v;
head[u]=idx;
return ;
}
int QueryLca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=t;i>=0;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=t;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
void TopSort(){
queue<int> q;
for(int i=1;i<=n;i++) if(!inv[i]) q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
if(!vec[x].size()) fa[x][0]=0,dep[x]=dep[0]+1,st[0].push_back(x);
else{
int lca=vec[x][0];
for(auto y:vec[x]) lca=QueryLca(lca,y);
fa[x][0]=lca,dep[x]=dep[lca]+1;st[lca].push_back(x);
for(int i=1;i<=t;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
}
for(int i=head[x];i;i=nex[i]){
int y=to[i];
inv[y]--;
if(!inv[y]) q.push(y);
}
}
return ;
}
void dfs(int x){
ans[x]=1;
for(auto y:st[x]) dfs(y),ans[x]+=ans[y];
return ;
}
int main(){
read(n);t=20;
for(int i=1;i<=n;i++){
int x;
while(1){
read(x);
if(!x) break;
add(x,i);vec[i].push_back(x);
inv[i]++;
}
}
TopSort();
dfs(0);
for(int i=1;i<=n;i++) write(ans[i]-1),putchar('\n');
return 0;
}
CF757F Team Rocket Rises Again(支配树+最短路)
CF757F Team Rocket Rises Again(支配树+最短路)
和上一道题的唯一区别就是,这里我们要求能使得最短路改变的边,那么很显然就是最短路网建出来就是上一题了。
直接跑一遍即可。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define ll long long
const int N=3e5+5;
const ll INF=1e18+7;
int head[N],nex[N<<1],to[N<<1],idx,id;
ll val[N<<1],dis[N],Maxn;
int fa[N][22],dep[N],inv[N],ans[N];
int n,m,S,len,t;
vector<int> vec[N],st[N],s[N],d[N];
bool vis[N];
void add(int u,int v,ll w){
nex[++idx]=head[u];
to[idx]=v;
val[idx]=w;
head[u]=idx;
return ;
}
int QueryLca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=t;i>=0;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=t;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
void TopSort(){
queue<int> q;
for(int i=1;i<=n;i++) if(!inv[i]) q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
if(!vec[x].size()) fa[x][0]=0,dep[x]=dep[0]+1,st[0].push_back(x);
else{
int lca=vec[x][0];
for(auto y:vec[x]) lca=QueryLca(lca,y);
fa[x][0]=lca,dep[x]=dep[lca]+1;st[lca].push_back(x);
for(int i=1;i<=t;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
}
for(auto y:d[x]){
inv[y]--;
if(!inv[y]) q.push(y);
}
}
return ;
}
struct node{
int x,fro;
ll dis;
node(int x=0,ll dis=0,int fro=0):x(x),dis(dis),fro(fro){}
inline bool operator < (const node B)const{return dis>B.dis;}
};
void dijkstra(){
priority_queue<node> q;
for(int i=1;i<=n;i++) dis[i]=INF;
dis[S]=0;q.push(node(S,0,0));
while(!q.empty()){
node r=q.top();q.pop();
int x=r.x;ll dist=r.dis;
if(dist<=dis[x]&&r.fro) vec[x].push_back(r.fro),d[r.fro].push_back(x),inv[x]++;
if(vis[x]) continue;vis[x]=true;
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(dis[y]>=dist+val[i]){
dis[y]=dist+val[i];
q.push(node(y,dis[y],x));
}
}
}
return ;
}
void dfs(int x){
ans[x]=1;
for(auto y:st[x]) dfs(y),ans[x]+=ans[y];
return ;
}
int main(){
read(n),read(m),read(S);t=20;
for(int i=1,u,v,w;i<=m;i++){
read(u),read(v),read(w);
add(u,v,w);
add(v,u,w);
}
dijkstra();
TopSort();
dfs(S);
for(int i=1;i<=n;i++) if(ans[i]>Maxn&&i!=S) Maxn=ans[i],id=i;
write(Maxn);
return 0;
}
4月7日
P4357 [CQOI2016]K 远点对(KD-Tree)
P4357 [CQOI2016]K 远点对(KD-Tree)
KDTree 模板题,首先就就是一个最优性剪枝,就是如果要去的这个矩形区域的最优答案都不能更新当前答案,那就直接不去了。
然后因为这里是求 \(k\) 远点对,所以要用一个堆来维护。
接下来要注意的是要提前存进去 \(2k\) 个元素,因为这里的点对是无序的,一个点对会算两次。
然后就是一个估价函数的设计,也就是当前点到当前矩形区域的最远距离,具体见代码。
代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define ll long long
#define int long long
const int N=1e5+5,INF=1e9+7;
const double alpha=0.68;
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val;
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline void Init(){root=0;Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;return ;}
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=1,sum(x)=val(x);
if(lc(x)) siz(x)+=siz(lc(x)),sum(x)+=sum(lc(x));
if(rc(x)) siz(x)+=sum(rc(x)),sum(x)+=sum(rc(x));
for(int i=0;i<2;i++) Min(x,i)=Max(x,i)=d(x,i);
for(int i=0;i<2;i++){
if(lc(x)){
Min(x,i)=min(Min(x,i),Min(lc(x),i)),
Max(x,i)=max(Max(x,i),Max(lc(x),i));
}
if(rc(x)){
Min(x,i)=min(Min(x,i),Min(rc(x),i)),
Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
}
return ;
}
inline bool cmp(point x,point y){return x.d[cmptype]<y.d[cmptype];}
void Build(int& x,int l,int r,int type){
if(l>r) return x=0,void();
int mid=(l+r)>>1;cmptype=type,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.d[0]<=d(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.d[1]<=d(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Rebuild(x,now);
return ;
}
int Query(int x,int L,int R,int D,int U){
if(!x||R<Min(x,0)||L>Max(x,0)||U<Min(x,1)||D>Max(x,1)) return 0;
if(L<=Min(x,0)&&Max(x,0)<=R&&D<=Min(x,1)&&Max(x,1)<=U) return sum(x);
int res=0;
if(L<=d(x,0)&&d(x,0)<=R&&D<=d(x,1)&&d(x,1)<=U) res+=val(x);
return Query(lc(x),L,R,D,U)+Query(rc(x),L,R,D,U)+res;
}
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
node T,Q;int Ans;
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
void QueryMax(int x){
if(!x) return;
Ans=max(Ans,Dis(T,t[x]));
int dl=GuessMax(lc(x)),dr=GuessMax(rc(x));
if(dl>dr){
if(dl>Ans) QueryMax(lc(x));
if(dr>Ans) QueryMax(rc(x));
}
else{
if(dr>Ans) QueryMax(rc(x));
if(dl>Ans) QueryMax(lc(x));
}
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],1ll*0),
res+=max(T.tp.d[i]-Max(x,i),1ll*0);
}
return res;
}
void QueryMin(int x){
if(!x) return;
int now=Dis(T,t[x]);
if(now) Ans=min(Ans,now);
int dl=GuessMin(lc(x)),dr=GuessMin(rc(x));
if(dl<dr){
if(dl<Ans) QueryMin(lc(x));
if(dr<Ans) QueryMin(rc(x));
}
else{
if(dr<Ans) QueryMin(rc(x));
if(dl<Ans) QueryMin(lc(x));
}
return ;
}
int Query(int x,int y,int type){
T.tp.d[0]=x,T.tp.d[1]=y;
if(type==0) Ans=INF,QueryMin(root);
else Ans=-INF,QueryMax(root);
return Ans;
}
inline ll Distance(node x,node y){return (x.tp.d[0]-y.tp.d[0])*(x.tp.d[0]-y.tp.d[0])+(x.tp.d[1]-y.tp.d[1])*(ll)(x.tp.d[1]-y.tp.d[1]);}
inline ll KGuessMin(int x){
ll res=0;
if(!x) return LLONG_MAX;
if(Min(x,0)>Q.tp.d[0]) res+=(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]);
if(Max(x,0)<Q.tp.d[0]) res+=(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]);
if(Min(x,1)>Q.tp.d[1]) res+=(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]);
if(Max(x,1)<Q.tp.d[1]) res+=(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]);
return res;
}
priority_queue<ll>q;
void KQueryMin(int x,int Now){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMin(lc(x)),dr=KGuessMin(rc(x));
if(now<q.top()&&x!=Now) q.pop(),q.push(now);
if(dl<dr){
if(dl<q.top()) KQueryMin(lc(x),Now);
if(dr<q.top()) KQueryMin(rc(x),Now);
}
else{
if(dr<q.top()) KQueryMin(rc(x),Now);
if(dl<q.top()) KQueryMin(lc(x),Now);
}
return ;
}
double FindKthMin(int x,int y,int k){
while(!q.empty()) q.pop();
for(int i=1;i<=k*2;i++) q.push(LLONG_MAX);
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMin(root,0);
return sqrt(q.top());
}
inline ll KGuessMax(int x){
if(x==0) return -LLONG_MAX;
ll res=0;
res+=max(1ll*(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]),1ll*(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]));
res+=max(1ll*(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]),1ll*(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]));
return res;
}
priority_queue<ll,vector<ll>,greater<ll> >qq;
void KQueryMax(int x){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMax(lc(x)),dr=KGuessMax(rc(x));
if(now>qq.top()) qq.pop(),qq.push(now);
if(dl>dr){
if(dl>qq.top()) KQueryMax(lc(x));
if(dr>qq.top()) KQueryMax(rc(x));
}
else{
if(dr>qq.top()) KQueryMax(rc(x));
if(dl>qq.top()) KQueryMax(lc(x));
}
return ;
}
ll FindKthMax(int x,int y,int k){
//while(!qq.empty()) qq.pop();
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMax(root);
return 1;
}
};
using namespace KDTree;
int n,k;
signed main(){
read(n),read(k);
for(int i=1;i<=n;i++) read(p[i].d[0]),read(p[i].d[1]);
Init();
Build(root,1,n,0);
for(int i=1;i<=k*2;i++) qq.push(-LLONG_MAX);
for(int i=1;i<=n;i++) FindKthMax(d(i,0),d(i,1),k);
write(qq.top());
return 0;
}
P1429 平面最近点对(加强版)(KD-Tree)
KD-Tree 求平面最近点对板题。
首先这里就可以不用使用堆来维护了,但是为了方便还是直接 ctrl+v 的。
然后这里和上一题的唯一区别就是一个最近一个最远。
但是要注意的是这里的估价函数变成了离四边界的距离之和,如果在矩形内部,则估价为 0 。
然后就没有了,需要注意的就是编号和当前询问的点的编号不能一样(不然就是自己和自己,距离为 0 了。)
代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define int long long
#define ll long long
const int N=2e5+5,INF=1e9+7;
const double alpha=0.68;
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val,id;
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline void Init(){root=0;Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;return ;}
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=1,sum(x)=val(x);
if(lc(x)) siz(x)+=siz(lc(x)),sum(x)+=sum(lc(x));
if(rc(x)) siz(x)+=sum(rc(x)),sum(x)+=sum(rc(x));
for(int i=0;i<2;i++) Min(x,i)=Max(x,i)=d(x,i);
for(int i=0;i<2;i++){
if(lc(x)){
Min(x,i)=min(Min(x,i),Min(lc(x),i)),
Max(x,i)=max(Max(x,i),Max(lc(x),i));
}
if(rc(x)){
Min(x,i)=min(Min(x,i),Min(rc(x),i)),
Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
}
return ;
}
inline bool cmp(point x,point y){return x.d[cmptype]<y.d[cmptype];}
void Build(int& x,int l,int r,int type){
if(l>r) return x=0,void();
int mid=(l+r)>>1;cmptype=type,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.d[0]<=d(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.d[1]<=d(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Rebuild(x,now);
return ;
}
int Query(int x,int L,int R,int D,int U){
if(!x||R<Min(x,0)||L>Max(x,0)||U<Min(x,1)||D>Max(x,1)) return 0;
if(L<=Min(x,0)&&Max(x,0)<=R&&D<=Min(x,1)&&Max(x,1)<=U) return sum(x);
int res=0;
if(L<=d(x,0)&&d(x,0)<=R&&D<=d(x,1)&&d(x,1)<=U) res+=val(x);
return Query(lc(x),L,R,D,U)+Query(rc(x),L,R,D,U)+res;
}
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
node T,Q;int Ans;
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
void QueryMax(int x){
if(!x) return;
Ans=max(Ans,Dis(T,t[x]));
int dl=GuessMax(lc(x)),dr=GuessMax(rc(x));
if(dl>dr){
if(dl>Ans) QueryMax(lc(x));
if(dr>Ans) QueryMax(rc(x));
}
else{
if(dr>Ans) QueryMax(rc(x));
if(dl>Ans) QueryMax(lc(x));
}
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],1ll*0),
res+=max(T.tp.d[i]-Max(x,i),1ll*0);
}
return res;
}
void QueryMin(int x){
if(!x) return;
int now=Dis(T,t[x]);
if(now) Ans=min(Ans,now);
int dl=GuessMin(lc(x)),dr=GuessMin(rc(x));
if(dl<dr){
if(dl<Ans) QueryMin(lc(x));
if(dr<Ans) QueryMin(rc(x));
}
else{
if(dr<Ans) QueryMin(rc(x));
if(dl<Ans) QueryMin(lc(x));
}
return ;
}
int Query(int x,int y,int type){
T.tp.d[0]=x,T.tp.d[1]=y;
if(type==0) Ans=INF,QueryMin(root);
else Ans=-INF,QueryMax(root);
return Ans;
}
inline ll Distance(node x,node y){return (x.tp.d[0]-y.tp.d[0])*(x.tp.d[0]-y.tp.d[0])+(x.tp.d[1]-y.tp.d[1])*(x.tp.d[1]-y.tp.d[1]);}
inline ll KGuessMin(int x){
ll res=0;
if(!x) return LLONG_MAX;
if(Min(x,0)>Q.tp.d[0]) res+=(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]);
if(Max(x,0)<Q.tp.d[0]) res+=(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]);
if(Min(x,1)>Q.tp.d[1]) res+=(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]);
if(Max(x,1)<Q.tp.d[1]) res+=(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]);
return res;
}
struct Node{
ll val;int id;
inline bool operator < (const Node &B)const{return (val==B.val)?(id>B.id):(val<B.val);}
inline bool operator > (const Node &B)const{return (val==B.val)?(id<B.id):(val>B.val);}
};
priority_queue<Node>q;
void KQueryMin(int x,int Now){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMin(lc(x)),dr=KGuessMin(rc(x));
if(now<q.top().val&&t[x].tp.id!=Now) q.pop(),q.push((Node){now,t[x].tp.id});
if(dl<dr){
if(dl<q.top().val) KQueryMin(lc(x),Now);
if(dr<q.top().val) KQueryMin(rc(x),Now);
}
else{
if(dr<q.top().val) KQueryMin(rc(x),Now);
if(dl<q.top().val) KQueryMin(lc(x),Now);
}
return ;
}
ll FindKthMin(int x,int y,int k,int qid){
while(!q.empty()) q.pop();
for(int i=1;i<=k;i++) q.push((Node){LLONG_MAX,0});
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMin(root,qid);
return q.top().val;
}
inline ll KGuessMax(int x){
if(x==0) return -LLONG_MAX;
ll res=0;
res+=max(1ll*(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]),1ll*(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]));
res+=max(1ll*(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]),1ll*(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]));
return res;
}
priority_queue<Node,vector<Node>,greater<Node> >qq;
void KQueryMax(int x){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMax(lc(x)),dr=KGuessMax(rc(x));
if(now>qq.top().val) qq.pop(),qq.push((Node){now,t[x].tp.id});
else if(now==qq.top().val&&t[x].tp.id<qq.top().id) qq.pop(),qq.push((Node){now,t[x].tp.id});
if(dl>dr){
if(dl>=qq.top().val) KQueryMax(lc(x));
if(dr>=qq.top().val) KQueryMax(rc(x));
}
else{
if(dr>=qq.top().val) KQueryMax(rc(x));
if(dl>=qq.top().val) KQueryMax(lc(x));
}
return ;
}
ll FindKthMax(int x,int y,int k){
while(!qq.empty()) qq.pop();
for(int i=1;i<=k;i++) qq.push((Node){-1,0});
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMax(root);
return qq.top().id;
}
};
using namespace KDTree;
int n,k,m,pos[N];
signed main(){
read(n);Init();
for(int i=1;i<=n;i++) read(p[i].d[0]),read(p[i].d[1]),p[i].id=i;
Build(root,1,n,0);Ans=LLONG_MAX;
for(int i=1;i<=n;i++) pos[t[i].tp.id]=i;
for(int i=1,x,y;i<=n;i++){
x=t[pos[i]].tp.d[0],y=t[pos[i]].tp.d[1];
Ans=min(Ans,FindKthMin(x,y,1,i));
}
printf("%.4lf",sqrt(Ans));
return 0;
}
P4148 简单题(KD-Tree)
支持单点加矩阵查询。
直接 KD-Tree 硬上即可。
时间复杂度是 \(O(n\sqrt{n})\) 。
代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5,INF=1e9+7;
const double alpha=0.68;
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val;
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline void Init(){root=0;Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;return ;}
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=1,sum(x)=val(x);
if(lc(x)) siz(x)+=siz(lc(x)),sum(x)+=sum(lc(x));
if(rc(x)) siz(x)+=siz(rc(x)),sum(x)+=sum(rc(x));
for(int i=0;i<2;i++) Min(x,i)=Max(x,i)=d(x,i);
for(int i=0;i<2;i++){
if(lc(x)){
Min(x,i)=min(Min(x,i),Min(lc(x),i)),
Max(x,i)=max(Max(x,i),Max(lc(x),i));
}
if(rc(x)){
Min(x,i)=min(Min(x,i),Min(rc(x),i)),
Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
}
return ;
}
inline bool cmp(point x,point y){return x.d[cmptype]<y.d[cmptype];}
void Build(int& x,int l,int r,int type){
if(l>r) return x=0,void();
int mid=(l+r)>>1;cmptype=type,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.d[0]<=d(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.d[1]<=d(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Rebuild(x,now);
return ;
}
int Query(int x,int L,int R,int D,int U){
if(!x||R<Min(x,0)||L>Max(x,0)||U<Min(x,1)||D>Max(x,1)) return 0;
if(L<=Min(x,0)&&Max(x,0)<=R&&D<=Min(x,1)&&Max(x,1)<=U) return sum(x);
int res=0;
if(L<=d(x,0)&&d(x,0)<=R&&D<=d(x,1)&&d(x,1)<=U) res+=val(x);
return Query(lc(x),L,R,D,U)+Query(rc(x),L,R,D,U)+res;
}
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
node T;int Ans;
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
void QueryMax(int x){
if(!x) return;
Ans=max(Ans,Dis(T,t[x]));
int dl=GuessMax(lc(x)),dr=GuessMax(rc(x));
if(dl>dr){
if(dl>Ans) QueryMax(lc(x));
if(dr>Ans) QueryMax(rc(x));
}
else{
if(dr>Ans) QueryMax(rc(x));
if(dl>Ans) QueryMax(lc(x));
}
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],0),
res+=max(T.tp.d[i]-Max(x,i),0);
}
return res;
}
void QueryMin(int x){
if(!x) return;
int now=Dis(T,t[x]);
if(now) Ans=min(Ans,now);
int dl=GuessMin(lc(x)),dr=GuessMin(rc(x));
if(dl<dr){
if(dl<Ans) QueryMin(lc(x));
if(dr<Ans) QueryMin(rc(x));
}
else{
if(dr<Ans) QueryMin(rc(x));
if(dl<Ans) QueryMin(lc(x));
}
return ;
}
int Query(int x,int y,int type){
T.tp.d[0]=x,T.tp.d[1]=y;
if(type==0) Ans=INF,QueryMin(root);
else Ans=-INF,QueryMax(root);
return Ans;
}
};
using namespace KDTree;
int n;
int main(){
int las=0;
read(n);
Init();
while(1){
int op;
read(op);
if(op==1){
int x,y,v;read(x),read(y),read(v);
x^=las,y^=las,v^=las;
Modify(root,(point){x,y,v},0);
}
else if(op==2){
int L,R,U,D;
read(L),read(D),read(R),read(U);
L^=las,R^=las,U^=las,D^=las;
las=Query(root,L,R,D,U);
write(las),putchar('\n');
}
else return 0;
}
return 0;
}
P4475 巧克力王国(KD-Tree)
发现信息有二维,于是可以考虑 KD-Tree 暴力搜索。
然后注意这里的剪枝:如果四边界都满足条件,那么这个矩阵都满足条件,直接返回 \(sum\) ,如果都不满足,那么矩阵内的点一定不满足,返回 \(0\) 即可。
剩下的递归下去暴力判断。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=5e4+5;
#define int long long
const int INF=1e18+7;
const double alpha=0.68;
int n,m,k;
struct point{int val[2],now;};
struct KDTree{
int lc,rc,siz,sum,Max[2],Min[2];
point tp;
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define val(x,i) t[x].tp.val[i]
#define Max(x,i) t[x].Max[i]
#define Min(x,i) t[x].Min[i]
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define now(x) t[x].tp.now
#define tp(x) t[x].tp
}t[N],q[N];
int root,rub[N],Top,cur,nowd;
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=siz(lc(x))+1+siz(rc(x));
sum(x)=sum(lc(x))+now(x)+sum(rc(x));
Max(x,0)=max(max(Max(lc(x),0),Max(rc(x),0)),val(x,0));
Max(x,1)=max(max(Max(lc(x),1),Max(rc(x),1)),val(x,1));
Min(x,0)=min(min(Min(lc(x),0),Min(rc(x),0)),val(x,0));
Min(x,1)=min(min(Min(lc(x),1),Min(rc(x),1)),val(x,1));
return ;
}
point p[N];
inline bool cmp(point x,point y){return x.val[nowd]<y.val[nowd];}
void Build(int &x,int l,int r,int now){
int mid=l+r>>1;nowd=now,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
if(l<mid) Build(lc(x),l,mid-1,now^1);
if(r>mid) Build(rc(x),mid+1,r,now^1);
Pushup(x);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
int top,Now,Nid;
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.val[0]<=val(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.val[1]<=val(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Now=x,Nid=now;
return ;
}
inline bool calc(int x,int y,int a,int b,int c){return a*x+b*y<c;}
int Query(int x,int d1,int d2,int Sum){
int res=0;
res+=calc(Max(x,0),Max(x,1),d1,d2,Sum);
res+=calc(Max(x,0),Min(x,1),d1,d2,Sum);
res+=calc(Min(x,0),Max(x,1),d1,d2,Sum);
res+=calc(Min(x,0),Min(x,1),d1,d2,Sum);
if(res==4) return sum(x);
if(res==0) return 0;
res=0;
if(calc(val(x,0),val(x,1),d1,d2,Sum)) res+=now(x);
if(lc(x)) res+=Query(lc(x),d1,d2,Sum);
if(rc(x)) res+=Query(rc(x),d1,d2,Sum);
return res;
}
signed main(){
int las=0;
read(n),read(m);
Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;
for(int i=1;i<=n;i++) read(p[i].val[0]),read(p[i].val[1]),read(p[i].now);
Build(root,1,n,0);
for(int i=1,x,y,z;i<=m;i++) read(x),read(y),read(z),write(Query(root,x,y,z)),putchar('\n');
return 0;
}
4月8日
P2479 [SDOI2010]捉迷藏(KD-Tree)
求一个点使得距离的极差最小,这里的距离是曼哈顿距离。
和欧几里得距离很相似,只不过这里要改变的就是距离计算公式和估价函数:
node T;int Ans;
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],0),
res+=max(T.tp.d[i]-Max(x,i),0);
}
return res;
}
完整代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5,INF=1e9+7;
const double alpha=0.68;
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val;
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline void Init(){root=0;Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;return ;}
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=1,sum(x)=val(x);
if(lc(x)) siz(x)+=siz(lc(x)),sum(x)+=sum(lc(x));
if(rc(x)) siz(x)+=sum(rc(x)),sum(x)+=sum(rc(x));
for(int i=0;i<2;i++) Min(x,i)=Max(x,i)=d(x,i);
for(int i=0;i<2;i++){
if(lc(x)){
Min(x,i)=min(Min(x,i),Min(lc(x),i)),
Max(x,i)=max(Max(x,i),Max(lc(x),i));
}
if(rc(x)){
Min(x,i)=min(Min(x,i),Min(rc(x),i)),
Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
}
return ;
}
inline bool cmp(point x,point y){return x.d[cmptype]<y.d[cmptype];}
void Build(int& x,int l,int r,int type){
if(l>r) return x=0,void();
int mid=(l+r)>>1;cmptype=type,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.d[0]<=d(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.d[1]<=d(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Rebuild(x,now);
return ;
}
int Query(int x,int L,int R,int D,int U){
if(!x||R<Min(x,0)||L>Max(x,0)||U<Min(x,1)||D>Max(x,1)) return 0;
if(L<=Min(x,0)&&Max(x,0)<=R&&D<=Min(x,1)&&Max(x,1)<=U) return sum(x);
int res=0;
if(L<=d(x,0)&&d(x,0)<=R&&D<=d(x,1)&&d(x,1)<=U) res+=val(x);
return Query(lc(x),L,R,D,U)+Query(rc(x),L,R,D,U)+res;
}
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
node T;int Ans;
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
void QueryMax(int x){
if(!x) return;
Ans=max(Ans,Dis(T,t[x]));
int dl=GuessMax(lc(x)),dr=GuessMax(rc(x));
if(dl>dr){
if(dl>Ans) QueryMax(lc(x));
if(dr>Ans) QueryMax(rc(x));
}
else{
if(dr>Ans) QueryMax(rc(x));
if(dl>Ans) QueryMax(lc(x));
}
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],0),
res+=max(T.tp.d[i]-Max(x,i),0);
}
return res;
}
void QueryMin(int x){
if(!x) return;
int now=Dis(T,t[x]);
if(now) Ans=min(Ans,now);
int dl=GuessMin(lc(x)),dr=GuessMin(rc(x));
if(dl<dr){
if(dl<Ans) QueryMin(lc(x));
if(dr<Ans) QueryMin(rc(x));
}
else{
if(dr<Ans) QueryMin(rc(x));
if(dl<Ans) QueryMin(lc(x));
}
return ;
}
int Query(int x,int y,int type){
T.tp.d[0]=x,T.tp.d[1]=y;
if(type==0) Ans=INF,QueryMin(root);
else Ans=-INF,QueryMax(root);
return Ans;
}
};
using namespace KDTree;
int n;
int main(){
read(n);
for(int i=1;i<=n;i++) read(p[i].d[0]),read(p[i].d[1]);
Build(root,1,n,0);
int ans=INF;
for (int i=1;i<=n;i++){
int x=d(i,0),y=d(i,1);
int Max=Query(x,y,1),Min=Query(x,y,0);
ans=min(ans,Max-Min);
}
write(ans);
return 0;
}
P2093 [国家集训队]JZPFAR(KD-Tree)
每次询问 \(n\) 个点当中距离一个点第 k 大的点的编号。
求编号就必须写一个结构体的堆来存,其他的没有区别。
具体见代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define int long long
#define ll long long
const int N=1e5+5,INF=1e9+7;
const double alpha=0.68;
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val,id;
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline void Init(){root=0;Max(root,0)=Max(root,1)=-INF,Min(root,0)=Min(root,1)=INF;return ;}
inline int NewNode(){
if(Top) return rub[Top--];
else return ++cur;
}
inline void Pushup(int x){
siz(x)=1,sum(x)=val(x);
if(lc(x)) siz(x)+=siz(lc(x)),sum(x)+=sum(lc(x));
if(rc(x)) siz(x)+=sum(rc(x)),sum(x)+=sum(rc(x));
for(int i=0;i<2;i++) Min(x,i)=Max(x,i)=d(x,i);
for(int i=0;i<2;i++){
if(lc(x)){
Min(x,i)=min(Min(x,i),Min(lc(x),i)),
Max(x,i)=max(Max(x,i),Max(lc(x),i));
}
if(rc(x)){
Min(x,i)=min(Min(x,i),Min(rc(x),i)),
Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
}
return ;
}
inline bool cmp(point x,point y){return x.d[cmptype]<y.d[cmptype];}
void Build(int& x,int l,int r,int type){
if(l>r) return x=0,void();
int mid=(l+r)>>1;cmptype=type,x=NewNode();
nth_element(p+l,p+mid,p+r+1,cmp),tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void dfs(int x,int num){
if(lc(x)) dfs(lc(x),num);
p[siz(lc(x))+num+1]=tp(x),rub[++Top]=x;
if(rc(x)) dfs(rc(x),num+siz(lc(x))+1);
return ;
}
inline bool Balanced(int x){return (double)max(siz(lc(x)),siz(rc(x)))<=(double)siz(x)*alpha;}
void Rebuild(int &x,int now){dfs(x,0);Build(x,1,siz(x),now);return ;}
void Modify(int &x,point v,int now){
if(!x) return x=NewNode(),lc(x)=rc(x)=0,tp(x)=v,Pushup(x),void();
if(!now) Modify(v.d[0]<=d(x,0)?lc(x):rc(x),v,now^1);
else Modify(v.d[1]<=d(x,1)?lc(x):rc(x),v,now^1);
Pushup(x);
if(!Balanced(x)) Rebuild(x,now);
return ;
}
int Query(int x,int L,int R,int D,int U){
if(!x||R<Min(x,0)||L>Max(x,0)||U<Min(x,1)||D>Max(x,1)) return 0;
if(L<=Min(x,0)&&Max(x,0)<=R&&D<=Min(x,1)&&Max(x,1)<=U) return sum(x);
int res=0;
if(L<=d(x,0)&&d(x,0)<=R&&D<=d(x,1)&&d(x,1)<=U) res+=val(x);
return Query(lc(x),L,R,D,U)+Query(rc(x),L,R,D,U)+res;
}
inline int Dis(node k1,node k2){return abs(k1.tp.d[0]-k2.tp.d[0])+abs(k1.tp.d[1]-k2.tp.d[1]);}
node T,Q;int Ans;
int GuessMax(int x){
if(x==0) return -INF;
int res=0;
for(int i=0;i<2;i++) res+=max(abs(T.tp.d[i]-Min(x,i)),abs(T.tp.d[i]-Max(x,i)));
return res;
}
void QueryMax(int x){
if(!x) return;
Ans=max(Ans,Dis(T,t[x]));
int dl=GuessMax(lc(x)),dr=GuessMax(rc(x));
if(dl>dr){
if(dl>Ans) QueryMax(lc(x));
if(dr>Ans) QueryMax(rc(x));
}
else{
if(dr>Ans) QueryMax(rc(x));
if(dl>Ans) QueryMax(lc(x));
}
}
int GuessMin(int x){
if(x==0) return INF;
int res=0;
for(int i=0;i<2;i++){
res+=max(Min(x,i)-T.tp.d[i],1ll*0),
res+=max(T.tp.d[i]-Max(x,i),1ll*0);
}
return res;
}
void QueryMin(int x){
if(!x) return;
int now=Dis(T,t[x]);
if(now) Ans=min(Ans,now);
int dl=GuessMin(lc(x)),dr=GuessMin(rc(x));
if(dl<dr){
if(dl<Ans) QueryMin(lc(x));
if(dr<Ans) QueryMin(rc(x));
}
else{
if(dr<Ans) QueryMin(rc(x));
if(dl<Ans) QueryMin(lc(x));
}
return ;
}
int Query(int x,int y,int type){
T.tp.d[0]=x,T.tp.d[1]=y;
if(type==0) Ans=INF,QueryMin(root);
else Ans=-INF,QueryMax(root);
return Ans;
}
inline ll Distance(node x,node y){return (x.tp.d[0]-y.tp.d[0])*(x.tp.d[0]-y.tp.d[0])+(x.tp.d[1]-y.tp.d[1])*(x.tp.d[1]-y.tp.d[1]);}
inline ll KGuessMin(int x){
ll res=0;
if(!x) return LLONG_MAX;
if(Min(x,0)>Q.tp.d[0]) res+=(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]);
if(Max(x,0)<Q.tp.d[0]) res+=(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]);
if(Min(x,1)>Q.tp.d[1]) res+=(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]);
if(Max(x,1)<Q.tp.d[1]) res+=(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]);
return res;
}
struct Node{
ll val;int id;
inline bool operator < (const Node &B)const{return (val==B.val)?(id>B.id):(val<B.val);}
inline bool operator > (const Node &B)const{return (val==B.val)?(id<B.id):(val>B.val);}
};
priority_queue<Node>q;
void KQueryMin(int x,int Now){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMin(lc(x)),dr=KGuessMin(rc(x));
if(now<q.top().val&&t[x].tp.id!=Now) q.pop(),q.push((Node){now,t[x].tp.id});
else if(now==q.top().val&&t[x].tp.id!=Now&&t[x].tp.id>q.top().id) q.pop(),q.push((Node){now,t[x].tp.id});
if(dl<dr){
if(dl<=q.top().val) KQueryMin(lc(x),Now);
if(dr<=q.top().val) KQueryMin(rc(x),Now);
}
else{
if(dr<=q.top().val) KQueryMin(rc(x),Now);
if(dl<=q.top().val) KQueryMin(lc(x),Now);
}
return ;
}
ll FindKthMin(int x,int y,int k){
while(!q.empty()) q.pop();
for(int i=1;i<=k*2;i++) q.push((Node){LLONG_MAX,0});
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMin(root,0);
return q.top().id;
}
inline ll KGuessMax(int x){
if(x==0) return -LLONG_MAX;
ll res=0;
res+=max(1ll*(Max(x,0)-Q.tp.d[0])*(Max(x,0)-Q.tp.d[0]),1ll*(Min(x,0)-Q.tp.d[0])*(Min(x,0)-Q.tp.d[0]));
res+=max(1ll*(Max(x,1)-Q.tp.d[1])*(Max(x,1)-Q.tp.d[1]),1ll*(Min(x,1)-Q.tp.d[1])*(Min(x,1)-Q.tp.d[1]));
return res;
}
priority_queue<Node,vector<Node>,greater<Node> >qq;
void KQueryMax(int x){
if(!x) return;
ll now=Distance(Q,t[x]),dl=KGuessMax(lc(x)),dr=KGuessMax(rc(x));
if(now>qq.top().val) qq.pop(),qq.push((Node){now,t[x].tp.id});
else if(now==qq.top().val&&t[x].tp.id<qq.top().id) qq.pop(),qq.push((Node){now,t[x].tp.id});
if(dl>dr){
if(dl>=qq.top().val) KQueryMax(lc(x));
if(dr>=qq.top().val) KQueryMax(rc(x));
}
else{
if(dr>=qq.top().val) KQueryMax(rc(x));
if(dl>=qq.top().val) KQueryMax(lc(x));
}
return ;
}
ll FindKthMax(int x,int y,int k){
while(!qq.empty()) qq.pop();
for(int i=1;i<=k;i++) qq.push((Node){-1,0});
Q.tp.d[0]=x,Q.tp.d[1]=y;
KQueryMax(root);
return qq.top().id;
}
};
using namespace KDTree;
int n,k,m;
signed main(){
read(n);Init();
for(int i=1;i<=n;i++) read(p[i].d[0]),read(p[i].d[1]),p[i].id=i;
Build(root,1,n,0);
read(m);
for(int i=1,x,y;i<=m;i++){
read(x),read(y),read(k);
write(FindKthMax(x,y,k)),putchar('\n');
}
return 0;
}
P4631 [APIO2018] Circle selection 选圆圈(KD-Tree)
P4631 [APIO2018] Circle selection 选圆圈(KD-Tree)
可以把圆近似成矩形,再使用 KD-Tree 爆搜即可。
于是这样爆搜,然后对每个结点检查一下就行了。
剪枝就是判断如果当前圆和矩形完全不交就直接返回,否则递归。
如果被卡了可以发挥人类智慧旋转所有点。
代码:
#include <bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
#define int long long
#define ll long long
const int N=3e5+5,INF=1e9+7;
const double alpha=0.68;
struct Node{
int x,y,r,id;
inline bool operator < (const Node &B)const{return r==B.r?id>B.id:r<B.r;}
}q[N];
int vis[N];
namespace KDTree{
int root,cnt,cmptype;
int rub[N],Top,cur;
struct point{
int d[2],val,id;
bool operator < (const point& k1)const{return d[cmptype]<k1.d[cmptype];}
}p[N];
struct node{
int siz,sum;
int Min[2],Max[2];
int lc,rc;
point tp;
bool operator < (const node& k1)const{return tp.d[cmptype]<k1.tp.d[cmptype];}
#define d(x,i) t[x].tp.d[i]
#define Min(x,i) t[x].Min[i]
#define Max(x,i) t[x].Max[i]
#define lc(x) t[x].lc
#define rc(x) t[x].rc
#define siz(x) t[x].siz
#define sum(x) t[x].sum
#define val(x) t[x].tp.val
#define tp(x) t[x].tp
}a[N],t[N];
inline int NewNode(){return Top?rub[Top--]:++cur;}
void Pushup(int x){
for(int i=0;i<2;i++) Min(x,i)=d(x,i)-val(x),Max(x,i)=d(x,i)+val(x);
for(int i=0;i<2;i++){
if(lc(x)) Min(x,i)=min(Min(x,i),Min(lc(x),i)),Max(x,i)=max(Max(x,i),Max(lc(x),i));
if(rc(x)) Min(x,i)=min(Min(x,i),Min(rc(x),i)),Max(x,i)=max(Max(x,i),Max(rc(x),i));
}
return ;
}
void Build(int &x,int l,int r,int type){
if(l>r) return ;
int mid=l+r>>1;x=NewNode(),cmptype=type;
nth_element(p+l,p+mid,p+r+1);tp(x)=p[mid];
Build(lc(x),l,mid-1,type^1);
Build(rc(x),mid+1,r,type^1);
Pushup(x);
return ;
}
void Query(int x,Node v){
if(!x||v.x+v.r<Min(x,0)||v.x-v.r>Max(x,0)||v.y+v.r<Min(x,1)||v.y-v.r>Max(x,1)) return ;
if((v.x-d(x,0))*(v.x-d(x,0))+(v.y-d(x,1))*(v.y-d(x,1))<=(v.r+val(x))*(v.r+val(x))&&!vis[t[x].tp.id]) vis[t[x].tp.id]=v.id;
Query(lc(x),v);
Query(rc(x),v);
return ;
}
};
using namespace KDTree;
int n,k,m;
signed main(){
read(n);
for(int i=1;i<=n;i++) read(q[i].x),p[i].d[0]=q[i].x,read(q[i].y),p[i].d[1]=q[i].y,read(q[i].r),p[i].val=q[i].r,q[i].id=p[i].id=i;
Build(root,1,n,0);
sort(q+1,q+n+1);
for(int i=n;i>=1;i--) if(!vis[q[i].id]) Query(root,q[i]);
for(int i=1;i<=n;i++) write(vis[i]),putchar(' ');
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号