主席树学习笔记
主席树学习笔记
1. 何为主席树
2. 主席树的实现
3. 主席树的基本运用
3. 1. 静态主席树、单点修改
3. 2. 静态主席树、区间修改
3. 3. 动态主席树
1.何为主席树
主席树即为可持久化线段树。关于持久化的定义,百度百科显示如下
持久化是将程序数据在持久状态和瞬时状态间转换的机制。通俗的讲,就是瞬时数据(比如内存中的数据,是不能永久保存的)持久化为持久数据(比如持久化至数据库中,能够长久保存)。(持久化是针对时间来说的)
拿主席树与一般的线段树对比,容易发现,一般的线段树只能保存现在的数据,不能访问到以前的数据,而主席树可以访问多个时间戳的数据,能够查询在某次更新之前的数据,实现了持久化。
2.主席树的实现
想要存储多个时间戳的数据,最朴素的想法是对应每个时间戳即每次更新建立一个线段树。事实上,主席树也正是应用了这个想法。然而建立这么多棵线段树会导致空间非常大,根本存不下。那么主席树是怎么实现建立多个线段树的同时又保证内存开的下呢?
我们发现,对于每次更新,每个线段树只会有\(log_2{n}\)个节点被更新。也就是说,按照朴素思路建立的多个线段树中大部分的节点都是相同重复的,这正是导致其空间超限的原因。而主席树对于每次更新,只会在上一个线段树的基础上建立\(log_2{n}\)个节点,先复制原来节点的信息,再进行更新,其他节点则连回原来的节点。可以看下面的图:
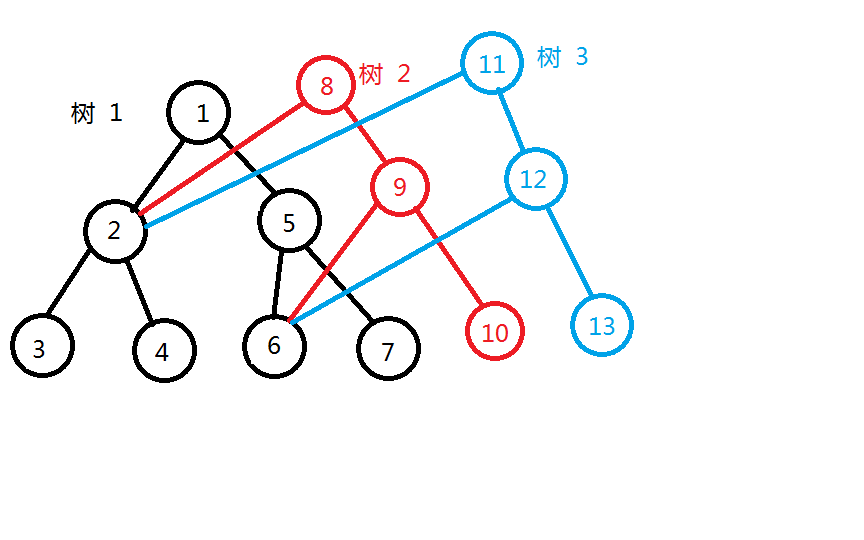
那么弄懂原理之后,主席树就好写了。
对于主席树,我们一般要开\(Rt[i],ls[i],rs[i]\)数组分别记录以i为根的主席树的编号,i的左儿子的编号,i的右儿子的编号。同时也要单独开一个数\(tot\)对节点进行编号。同时,由于主席树每次更新要重新建立\(log_2{n}\)个节点,总共至少需要\(nlog_2{n}\)个节点,因此我们一般开32倍空间。对于更新比较频繁的主席树,我们一般都是能开多大就开多大,否则有几率会RE掉。
主席树的各个操作跟线段树相似。
- build函数
void build(int L,int R,int &rt){
rt=++tot;
if(L==R)return ;
int mid=L+R>>1;
build(L,mid,ls[rt]);
build(mid+1,R,rs[rt]);
}
注:build函数可写可不写,因题而异。
- update函数
void update(int L,int R,int ot,int &rt,int x){
rt=++tot;
ls[rt]=ls[ot],rs[rt]=rs[ot],sum[rt]=sum[ot]+1;// 复制原来节点信息
if(L==R)return ;
int mid=(L+R)>>1;
if(x<=mid)update(L,mid,ls[ot],ls[rt],x);
else update(mid+1,R,rs[ot],rs[rt],x);
}
注:此处的update函数是单点更新,对于不同题目写法不同。
3.主席树的基本运用
-
区间第K值(静态主席树、单点修改)
题意:给定 \(n\) 个整数构成的序列 \(a\),将对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。
如果用线段树,我们的思路应该是用归并树二分查找。但这种写法耗时大且内存大,在很多地方都不能使用。
我们转换一下思路,如果题目给出的查询区间为 \([1,n]\),这题就变好写了。我们只需要将序列\(a\)进行离散化,然后建立一个权值线段树,直接在线段树里面找就行了。
代码如下:
int query(int L,int R,int p,int k){
if(L==R)return L;
int mid=L+R>>1;
if(sum[ls]>=k)return query(mid+1,R,ls,k);
else return query(mid+1,R,rs,k-sum[ls]);
}
然而,本题给出的查询区间是\([l,r]\),这该怎么解决呢?
这时候,我们可以使用我们的主席树了。我们容易发现,本题存在区间可加减性,即\([l,r]\)区间的信息可以通过\([1,r]\)减去\([1,l-1]\)得到(其实就是前缀和的思想)。那么我们对于\([1,i]\) 的每一个前缀就用主席树来维护。建树的时候,\([1,i]\)的主席树即在\([1,i-1]\)`主席树的基础上进行修改。
那么查询的时候,我们只需要用\([1,r]\)和\([1,l-1]\)对应的主席树相减查询。
int query(int L,int R,int x,int y,int k){
if(L==R)return L;
int res=sum[ls[y]]-sum[ls[x]],mid=L+R>>1;
if(res>=k)return query(L,mid+1,ls[x],ls[y],k);
else return query(mid+1,R,rs[x],rs[y],k-res);
}
完整代码如下:
#include<bits/stdc++.h>
#define M 100005
using namespace std;
int A[M],B[M],ls[M<<5],rs[M<<5],Rt[M],sum[M<<5],tot;
void build(int L,int R,int &rt){
rt=++tot;sum[rt]=0;
if(L==R)return ;
int mid=L+R>>1;
build(L,mid,ls[rt]),build(mid+1,R,rs[rt]);
}
void update(int L,int R,int ot,int &rt,int x){
rt=++tot;
ls[rt]=ls[ot],rs[rt]=rs[ot],sum[rt]=sum[ot]+1;
if(L==R)return ;
int mid=L+R>>1;
if(x<=mid)update(L,mid,ls[ot],ls[rt],x);
else update(mid+1,R,rs[ot],rs[rt],x);
}
int query(int L,int R,int x,int y,int k){
if(L==R)return L;
int res=sum[ls[y]]-sum[ls[x]],mid=L+R>>1;
if(res>=k)return query(L,mid+1,ls[x],ls[y],k);
else return query(mid+1,R,rs[x],rs[y],k-res);
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
B[i]=A[i];
}
sort(B+1,B+n+1);
int cnt=unique(B+1,B+n+1)-B-1;
tot=0;
build(1,cnt,Rt[0]);
for(int i=1;i<=n;i++){
A[i]=lower_bound(B+1,B+cnt+1,A[i])-B;
update(1,cnt,Rt[i-1],Rt[i],A[i]);
}
int L,R,k;
while(m--){
scanf("%d%d%d",&L,&R,&k);
printf("%d\n",B[query(1,cnt,Rt[L-1],Rt[R],k)]);
}
return 0;
}
同时,这里给出主席树区间可加减的原因:
主席树的每个节点保存的是一颗线段树,维护的区间信息,结构相同,因此具有可加减性
例题:
-
SP11470 To the moon(静态主席树、区间修改)
题意:
一个长度为n的数组,4种操作 :
(1)C l r d:区间[l,r]中的数都加1,同时当前的时间戳加1 。
(2)Q l r:查询当前时间戳区间[l,r]中所有数的和 。
(3)H l r t:查询时间戳t区间[l,r]的和 。
(4)B t:将当前时间戳置为t.
回到过去t时刻,t之后的信息都会消失,即就不会再向前跳跃。所有操作均合法 。
这题一看就知道是裸主席树,但不同的是,之前我们写的是单点修改,而这道题是要求区间修改。
我们回忆一下,对于线段树的区间修改,我们使用延迟更新,最终将区间内所有的节点都更新一遍。而主席树的儿子节点是共用的,如果按照这种写法,会导致之前版本受到影响。
这时候,我们就要标记永久化。
所谓标记永久化,就是直接修改被\([L,R]\)影响的区间,若此时递归到的区间被\([L,R]\)包含打上标记并且return,让标记永远待在被\([L,R]\)包含的第一级区间,不进行下传。查询的时候一路累加遇到的标记得出此时区间的真实值。
我们对比一下两份代码(以线段树为例)
延迟更新
void update(int L,int R,int ql,int qr,int p,int x){
if(ql<=L&&R<=qr){
sum[p]+=(R-L+1)*x;
lazy[p]+=x;
return ;
}
down(p);
int mid=L+R>>1;
if(qr<=mid)update(L,mid,ql,qr,ls,x);
else if(ql>mid)update(mid+1,R,ql,qr,rs,x);
else update(L,mid,ql,mid,ls,x),
update(mid+1,R,mid+1,qr,rs,x);
up(p);
}
int query(int L,int R,int ql,int qr,int p){
if(ql<=L&&R<=qr)return sum[p];
down(p);
int mid=L+R>>1;
if(qr<=mid)return query(L,mid,ql,qr,ls);
else if(ql>mid)return query(mid+1,R,ql,qr,rs);
else return query(L,mid,ql,mid,ls)+query(mid+1,R,mid+1,qr,rs);
}
标记永久化
void update(int L,int R,int ql,int qr,int p,int x){
sum[p]+=x*(min(R,qr)-max(L,ql)+1);
if(ql<=L&&R<=qr){
lazy[p]+=x;
return ;
}
int mid=L+R>>1;
if(qr<=mid)update(L,mid,ql,qr,ls,x);
else if(ql>mid)update(mid+1,R,ql,qr,rs,x);
else update(L,mid,ql,mid,ls,x),
update(mid+1,R,mid+1,qr,rs,x);
}
int query(int L,int R,int ql,int qr,int p,int add){
if(ql<=L&&R<=qr)return 1ll*add*(R-L+1)+sum[p];
int mid=L+R>>1;add+=lazy[p];
if(qr<=mid)return query(L,mid,ql,qr,ls,add);
else if(ql>mid)return query(mid+1,R,ql,qr,rs,add);
else return query(L,mid,ql,mid,ls,add)+query(mid+1,R,mid+1,qr,rs,add);
}
那么,代码也就不难写出了:
#include<bits/stdc++.h>
#define M 100005
using namespace std;
typedef long long LL;
int root[M],ls[M<<5],rs[M<<5],tot;
LL sum[M<<5],lazy[M<<5],A[M];
void build(int L,int R,int &rt){
rt=++tot;
if(L==R){
sum[rt]=A[L];
return ;
}
int mid=L+R>>1;
build(L,mid,ls[rt]);
build(mid+1,R,rs[rt]);
sum[rt]=sum[ls[rt]]+sum[rs[rt]];
}
void update(int L,int R,int ql,int qr,int p,int &rt,LL x){
rt=++tot;
ls[rt]=ls[p],rs[rt]=rs[p];
sum[rt]=sum[p]+1ll*(min(R,qr)-max(L,ql)+1)*x;
lazy[rt]=lazy[p];
if(ql<=L&&R<=qr){
lazy[rt]+=x;return ;
}
int mid=L+R>>1;
if(qr<=mid)update(L,mid,ql,qr,ls[p],ls[rt],x);
else if(ql>mid)update(mid+1,R,ql,qr,rs[p],rs[rt],x);
else{
update(L,mid,ql,mid,ls[p],ls[rt],x);
update(mid+1,R,mid+1,qr,rs[p],rs[rt],x);
}
}
LL query(int L,int R,int ql,int qr,int p,LL ad){
if(ql<=L&&R<=qr)return 1ll*ad*(R-L+1)+sum[p];
int mid=L+R>>1;ad+=lazy[p];
if(qr<=mid)return query(L,mid,ql,qr,ls[p],ad);
else if(ql>mid)return query(mid+1,R,ql,qr,rs[p],ad);
else return query(L,mid,ql,mid,ls[p],ad)+query(mid+1,R,mid+1,qr,rs[p],ad);
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%lld",&A[i]);
build(1,n,root[0]);
char op[5];
int now=0,L,R;
LL x;
while(m--){
scanf("%s",op);
if(op[0]=='C'){
scanf("%d%d%lld",&L,&R,&x);++now;
update(1,n,L,R,root[now-1],root[now],x);
}
if(op[0]=='Q'){
scanf("%d%d",&L,&R);
printf("%lld\n",query(1,n,L,R,root[now],0));
}
if(op[0]=='H'){
scanf("%d%d%lld",&L,&R,&x);
printf("%lld\n",query(1,n,L,R,root[x],0));
}
if(op[0]=='B'){
scanf("%lld",&x);now=x;
}
}
return 0;
}
-
Dynamic Rankings(动态主席树)
题意:给定一个含有n个数的序列a[1],a[2],a[3]……a[n],程序必须回答这样的询问:对于给定的i,j,k,在a[i],a[i+1],a[i+2]……a[j]中第k小的数是多少(1≤k≤j-i+1)。并且,你可以改变一些a[i]的值,改变后,程序还能针对改变后的a继续回答上面的问题。
区间第K值的变形,但不同的是,本题还要求修改其中的值,从静态主席树变成了动态主席树。如果我们继续按照之前的写法,修改一个值,就需要把后面的主席树全部修改一遍。那么修改一次的时间复杂度就变成了\(O(nlog_2n)\),总共修改的时间复杂度就变成了\(O(nmlog_2n)\),而\(N\le50000,M\le10000\),明显会超时。
那么我们继续思考:区间第K值中,主席树相当维护的是一个前缀和。而这道题会修改其中的值,再让我们求其前缀和。看到单点修改、求前缀和,我们很快就想到了树状数组。那么,我们就用树状数组套主席树,用树状数组维护下标,主席树维护权值。那么修改和查询一次就都变成了\(O(log_2(n)log_2(n))\),这个时间复杂度就变得非常的优秀了。
修改的时候,就像树状数组一样进行修改即可
for(int j=i;j<=n;j+=-j&j)
update(1,tot,A[i],root[j],root[j],1);
查询的时候就要开两个队列来存要相加减的版本编号
t1=0,t2=0;
for(int j=x-1;j;j-=-j&j)Q1[++t1]=root[j];
for(int j=y;j;j-=-j&j)Q2[++t2]=root[j];
printf("%d\n",B[query(1,tot,Q[i].k)]);
int query(int L,int R,int k){
if(L==R)return L;
int suml=0,mid=L+R>>1;
for(int i=1;i<=t1;i++)suml-=sum[ls[Q1[i]]];
for(int i=1;i<=t2;i++)suml+=sum[ls[Q2[i]]];
if(suml>=k){
for(int i=1;i<=t1;i++)Q1[i]=ls[Q1[i]];
for(int i=1;i<=t2;i++)Q2[i]=ls[Q2[i]];
return query(L,mid,k);
}
else{
for(int i=1;i<=t1;i++)Q1[i]=rs[Q1[i]];
for(int i=1;i<=t2;i++)Q2[i]=rs[Q2[i]];
return query(mid+1,R,k-suml);
}
}
完整代码如下:
#include<bits/stdc++.h>
#define M 100005
using namespace std;
int A[M],B[M<<1],sum[M*150],root[M],ls[M*150],rs[M*150],tot;
int Q1[M],Q2[M],t1,t2;
void update(int L,int R,int x,int p,int &rt,int a){
rt=++tot;sum[rt]=sum[p]+a,ls[rt]=ls[p],rs[rt]=rs[p];
if(L==R)return ;
int mid=L+R>>1;
if(x<=mid)update(L,mid,x,ls[p],ls[rt],a);
else update(mid+1,R,x,rs[p],rs[rt],a);
}
struct node{
int op,x,y,k;
}Q[M];
int query(int L,int R,int k){
if(L==R)return L;
int suml=0,mid=L+R>>1;
for(int i=1;i<=t1;i++)suml-=sum[ls[Q1[i]]];
for(int i=1;i<=t2;i++)suml+=sum[ls[Q2[i]]];
if(suml>=k){
for(int i=1;i<=t1;i++)Q1[i]=ls[Q1[i]];
for(int i=1;i<=t2;i++)Q2[i]=ls[Q2[i]];
return query(L,mid,k);
}
else{
for(int i=1;i<=t1;i++)Q1[i]=rs[Q1[i]];
for(int i=1;i<=t2;i++)Q2[i]=rs[Q2[i]];
return query(mid+1,R,k-suml);
}
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
B[i]=A[i];
}
int tot=n;
char op[5];
for(int i=1;i<=m;i++){
scanf("%s",op);
if(op[0]=='Q'){
scanf("%d%d%d",&Q[i].x,&Q[i].y,&Q[i].k);
Q[i].op=1;
}
else{
scanf("%d%d",&Q[i].x,&Q[i].y);
Q[i].op=2;B[++tot]=Q[i].y;
}
}
sort(B+1,B+tot+1);
tot=unique(B+1,B+tot+1)-B-1;
for(int i=1;i<=n;i++){
A[i]=lower_bound(B+1,B+tot+1,A[i])-B;
for(int j=i;j<=n;j+=-j&j)
update(1,tot,A[i],root[j],root[j],1);
}
int x,y;
for(int i=1;i<=m;i++){
x=Q[i].x,y=Q[i].y;
if(Q[i].op==2){
for(int j=x;j<=n;j+=-j&j)
update(1,tot,A[x],root[j],root[j],-1);
A[x]=lower_bound(B+1,B+tot+1,y)-B;
for(int j=x;j<=n;j+=-j&j)
update(1,tot,A[x],root[j],root[j],1);
}
else{
t1=0,t2=0;
for(int j=x-1;j;j-=-j&j)Q1[++t1]=root[j];
for(int j=y;j;j-=-j&j)Q2[++t2]=root[j];
printf("%d\n",B[query(1,tot,Q[i].k)]);
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号