SIMULINK仿真两车追赶的模糊控制系统

实验目的

理解模糊逻辑推理的原理及特点，熟练应用模糊推理。

实验内容

假设两汽车均为理想状态，即 ，Y为速度，U为油门控制输入。

（1）设计模糊控制器控制汽车由静止启动，追赶200m外时速90km的汽车并与其保持30m的距离。

（2）在25时刻前车速度改为时速110km时，仍与其保持30m距离。

（3）在35时刻前车速度改为时速70km时，仍与其保持30m距离。

要求：

（1）设计两输入一输出的模糊控制器，给出输入、输出语言变量的隶属函数图，模糊控制规则表，推论结果立体图。

（2）用SIMULINK仿真两车追赶的模糊控制系统，给出目标车的速度曲线图、油门踩放图、追赶车速度图、与前车相对距离图。

实验过程

（1）使用fuzzy工具箱配置模糊推理系统

Matlab命令行输入fuzzy，配置模糊系统，点击“Edit”设置2个输入1个输出。命名输入为r、theta1、输出为推力Throttle，各自论域分别为[0,1]、[-3,3]和[-1,1]，并设置隶属函数均为三角形，具体如图1、图2。

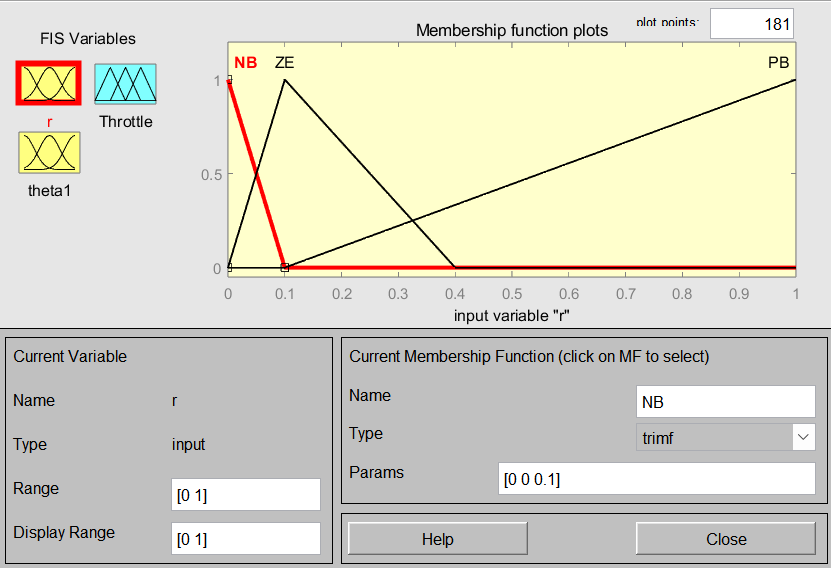
图1 输入语言变量r和theta的隶属函数图

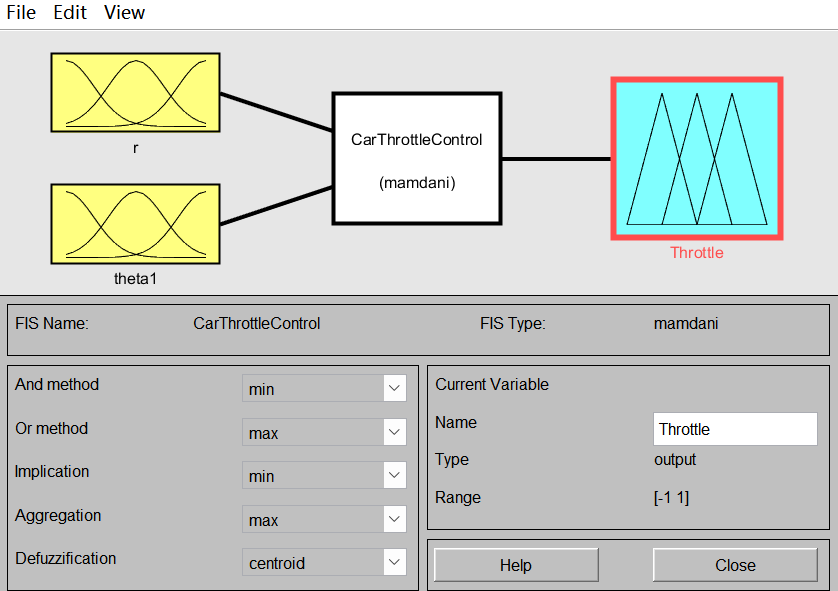
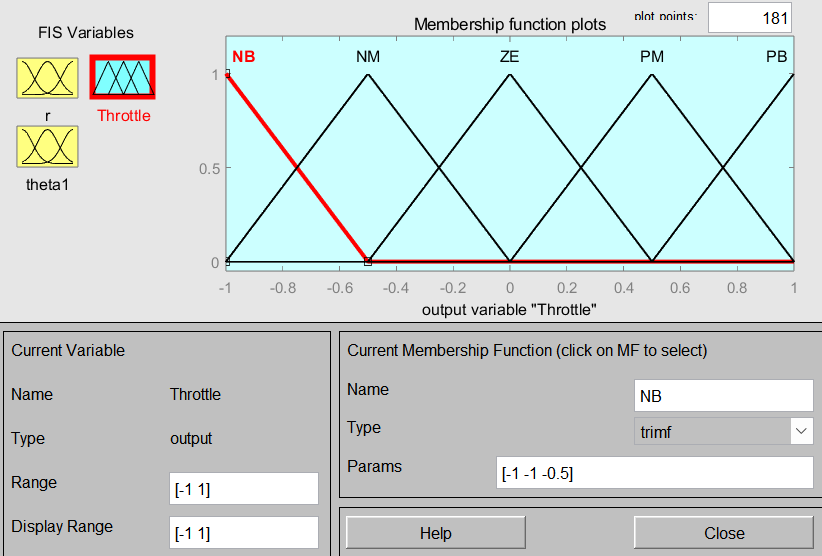
图2 输出语言变量Throttle隶属函数图

双击图2中的白色规则库模块，创建规则库如图3。

图3 模糊控制规则表

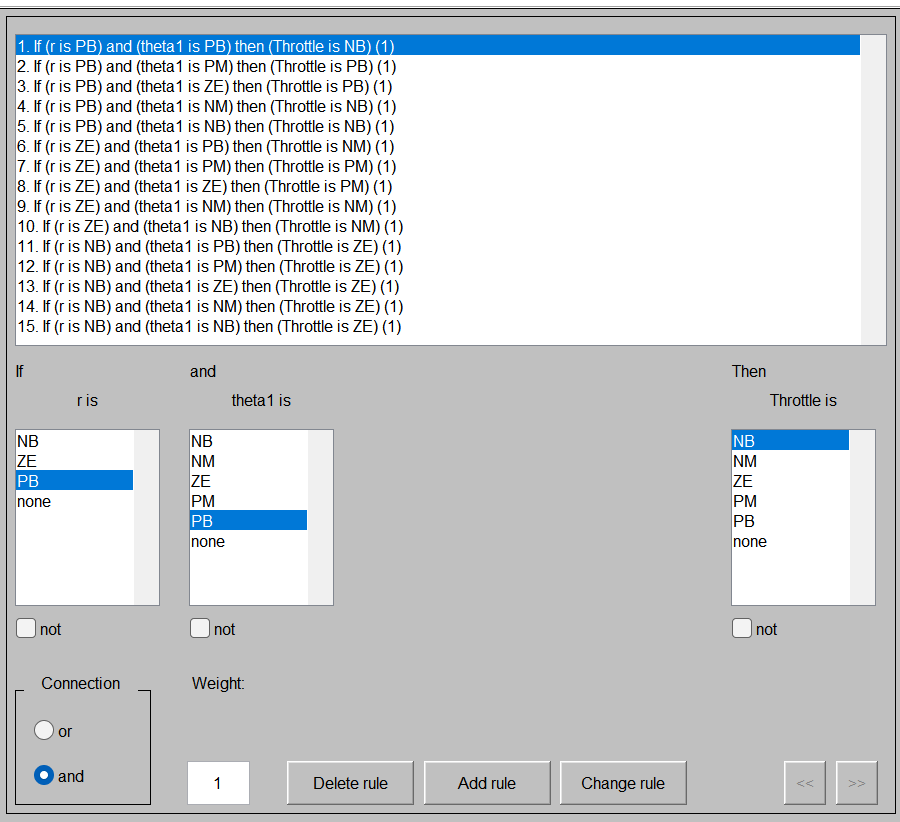
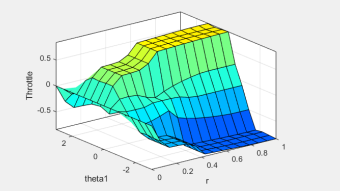
点击“View--Surface”可以查看Throttle(theta1,r)函数图以便直观理解映射关系，点击“View--Rule”可设置theta1和r的值查看对应的输出量，如图4。

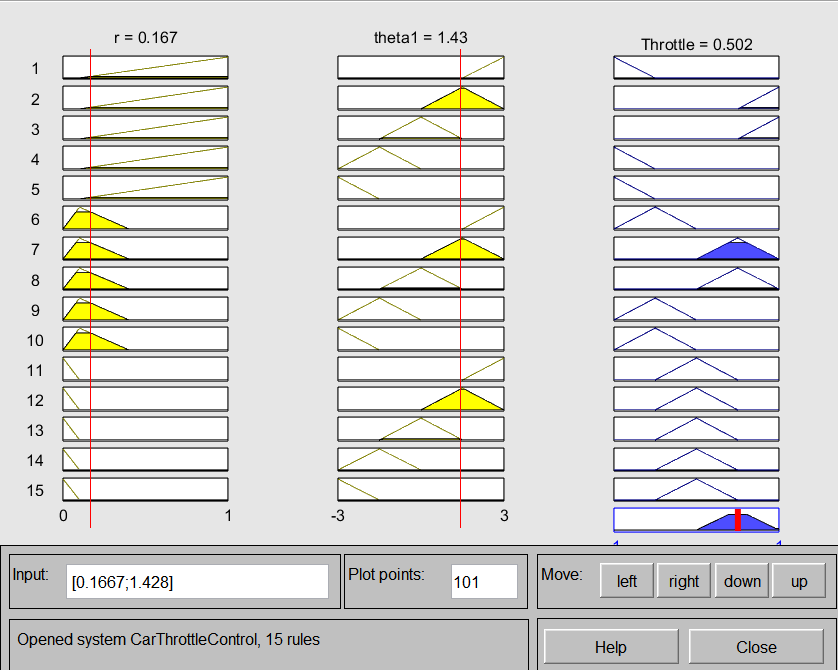
图4 模糊推理系统推论结果立体图

最后将建立好的FLS模糊推理系统保存，命名为“CarController.fis”。

（2）在simulink中设计两车追赶模糊控制系统

设计如下控制系统，在fuzz模块中导入模糊推理系统“CarController.fis”，根据题目要求设计simulink仿真追赶模型如图5。

图5 两车追赶模糊控制系统仿真

其中，从上到下三个阶跃函数的阶跃时间分别设为0、25、35，使得car1（被追赶）汽车时速90km，在25时刻速度改为时速110km，在35时刻速度改为时速70km。car1的速度变化如图6(a)所示。

使用积分函数1/s求得car1行驶路程，在设计函数f(u)=u*1000/3600+200将单位为km/h的速度转换为m/s再加200m，体现car1在car2的前200m处。

(a) car1速度曲线　　 (b) car2速度曲线

图6 两车速度曲线图

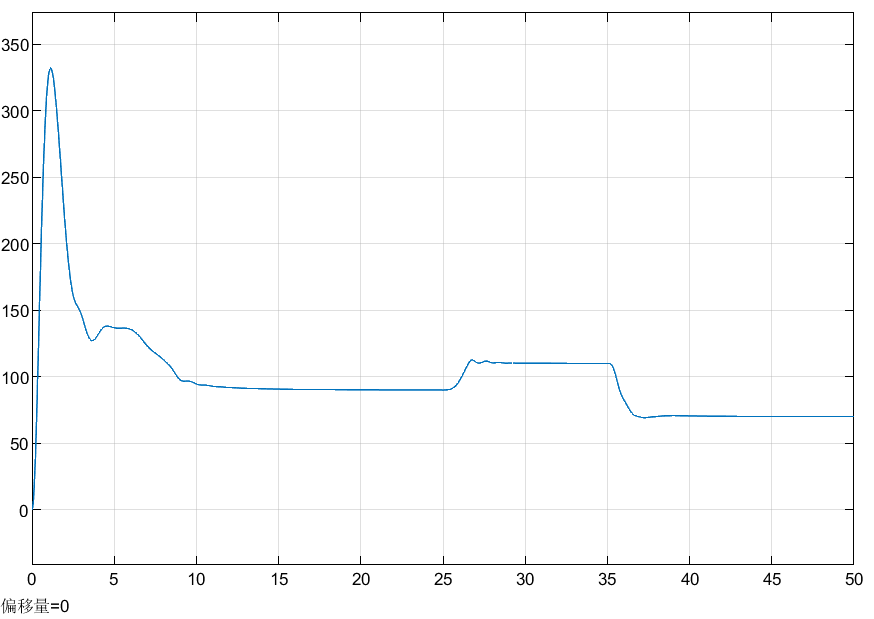
模糊逻辑控制器输出经过增益K=700放大，限幅函数上限设置为1000。将仿真时间设置为固定步长0.001，仿真结果如图6-图8所示。可以看到，最终两车相对距离保持30m左右，油门踩放趋于0。

图7 两车相对距离图

图8 追赶车油门踩放图

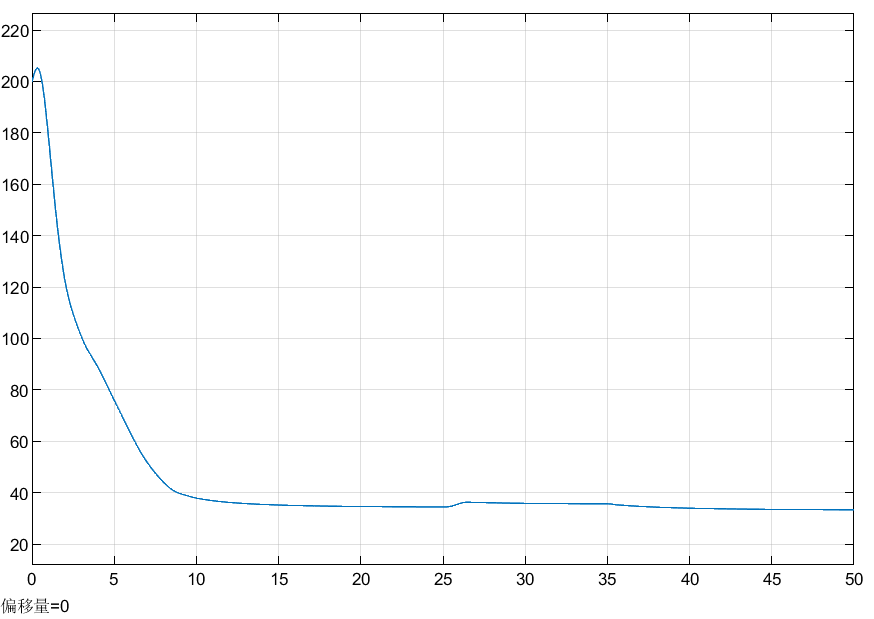
实验总结

模糊推理是一种基于模糊集合论的不确定推理方式，它通过模糊规则和隶属函数来描述和推理模糊关系。模糊集合是对经典集合的扩展，每个元素都有一个隶属度，表示其属于某个集合的程度（范围在0到1之间）。隶属函数用于确定元素的隶属度，常见的隶属函数有三角函数、梯形函数等。模糊关系R 是定义两个模糊集合 A 和 B之间的关系，其中每个元素的值表示对应元素之间的关系程度。