ABC176F Brave CHAIN（DP）

ABC176F Brave CHAIN

直接给转化题意.

给一个长度为 \(3n\) （\(n\le 2000\)）的整数序列 \(a\)，满足 \(1\le a_i\le n\) .

每次在序列的前五个数中任选三个删去，若这三个数相等，得分 \(+1\)，求最大得分. （只剩三个数时，若这三个数相等，得分 \(+1\) ）

---

考虑每次操作影响范围很有限度. \(i\) 次操作从前缀 \(3i+2\) 个数中选剩两个数，和剩余的数构成子问题，每次操作只需考虑前面剩的是哪两个数，和后缀开头确定的三个数，作为转移的考量.

可以想到设 \(f(i,x,y)\) 表示当前已经操作了 \(i\) 次，当前开头两个数为 \(x\) 和 \(y\)，最大的得分.

状态是立方级的，朴素转移每次是平方级的，总转移次数是立方级的. 考虑到状态量级已经超过限制，自然想到压维.

考虑去压掉第一维，因为转移是一个取 \(\max\) 的操作，\(f(i,x,y)\rightarrow f(i+1,x,y)\) 是一条固定的转移，也就是状态答案是递增的，所以第一维是可以压掉的. 于是状态设为 \(f(x,y)\).

接着考虑转移. 每次转移需要对新三个数作考虑，与这三个数无关的状态将不会更新，所以每次转移最多只会影响三行三列的答案. 于是更新状态次数的量级变为平方级，来到了限制内.

随后考虑每个状态转移的复杂度. 手玩之后可以发现转移方式是取点/行/列/所有状态的 \(\max\)，因为 \(\max\) 运算的良好的单调性质这些全都可以 \(\mathrm O(1)\) 更新维护，单个状态转移的复杂度也变为 \(\mathrm O(1)\).

最后就是认真理好具体转移细节.

本来想调整好转移的顺序防止冲突，不过因为只影响三行三列答案，直接开个 \(temp(x,y)\) 存新一层答案，转移完再反赋回去会更好.

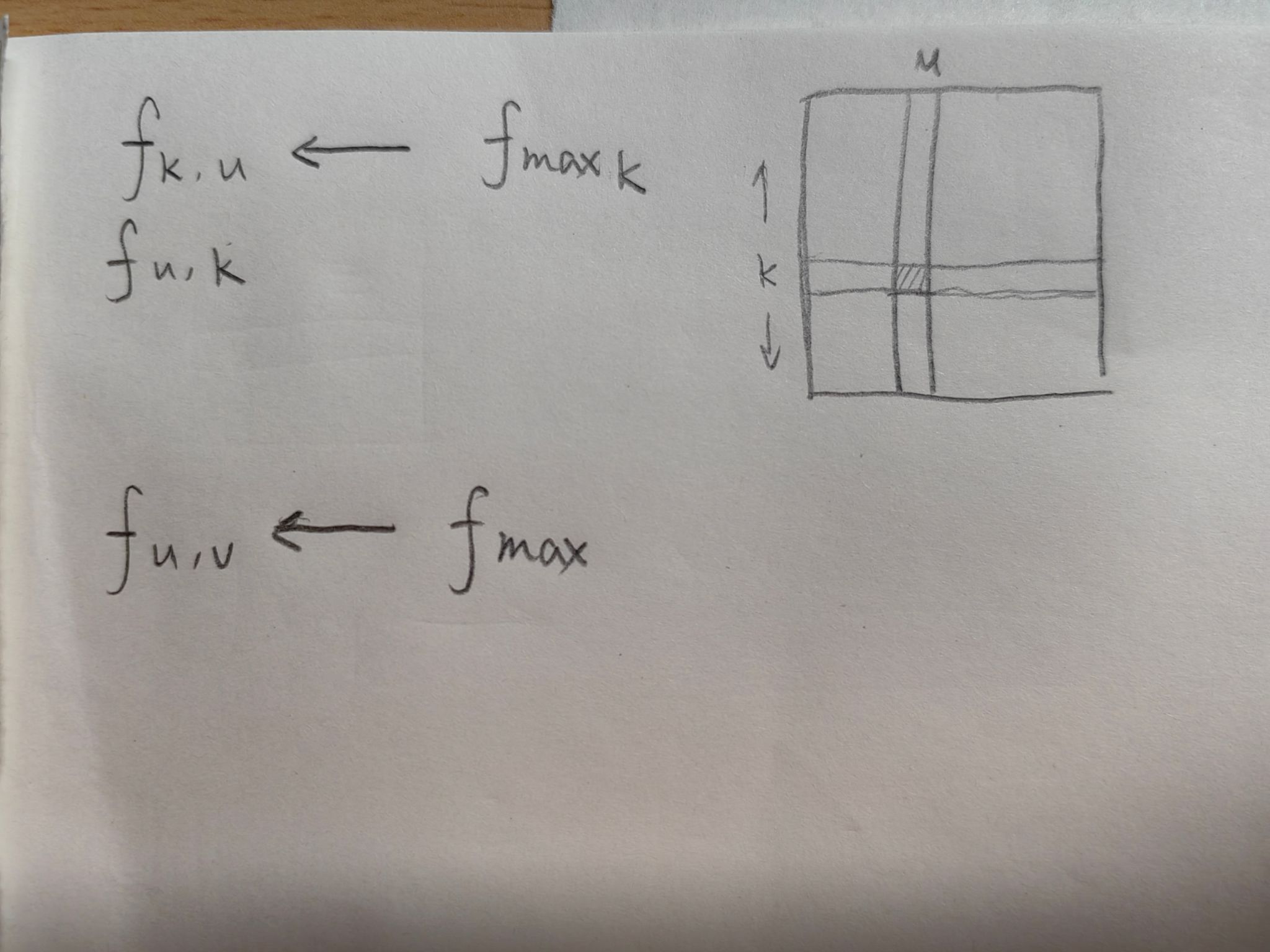
没带数位板就手写一下了

写的时候脑子抽了一下，给连续三个相同的情况多做了一种转移，导致调了半天. 我是笨比，细心程度有待提升.

以此为机会尝试了一下 vector 开多维数组、传列表参、lambda 表达式的用法.

正常设法的 \(f(x,y)\) 中 \(x\) 和 \(y\) 是有序的，选择了无序的写法，会不会反而写起来更丑了（）

template <class T>
void pmax(T &b,T t)
{
	b=max(b,t);
	return;
}
template <class T,class... A>
void pmax(T &b,T t,A... rest)
{
	b=max(b,t);
	pmax(b,rest...);
	return;
}
void R()
{
	int n,N,del=0;
	cin>>n; N=3*n;
	int fmaxall=-1;
	vector<int> a(3*n),fmax(n+1);
	vector<vector<int>> f(n+1,vector<int>(n+1)),temp(n+1,vector<int>(n+1));
	for (int &x:a) cin>>x;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			f[i][j]=temp[i][j]=-1;
	for (int i=1;i<=n;i++)
		fmax[i]=-1;
	f[a[0]][a[1]]=f[a[1]][a[0]]=0;
	fmaxall=fmax[a[0]]=fmax[a[1]]=0;
	auto d=[](int A)->int { return A==-1?-1:A+1; };

	for (int i=2,u,v,w;i<N-1;i+=3)
	{
		u=a[i],v=a[i+1],w=a[i+2];
		if (u==w) swap(v,w);
		if (v==w) swap(u,w);
		if (u==v&&v==w) { del++; }
		else
		{
			for (int j=i;j<=i+2;j++)
				for (int k=1;k<=n;k++)
				{
					pmax(temp[k][a[j]],fmax[k]);
					pmax(temp[a[j]][k],fmax[k]);
				}
			temp[u][v]=temp[v][u]=temp[u][w]=temp[w][u]=temp[v][w]=temp[w][v]=fmaxall;

		}
		if (u==v&&v==w) {}
		else if (u==v)
		{
			for (int k=1;k<=n;k++)
			{
				pmax(temp[w][k],f[w][k],d(f[u][k]));
				pmax(temp[k][w],f[k][w],d(f[k][u]));
			}
			pmax(temp[u][u],f[u][u],d(f[w][w]));
		}
		else
		{
			pmax(temp[v][w],f[v][w],d(f[u][u])); temp[w][v]=temp[v][w];
			pmax(temp[u][w],f[u][w],d(f[v][v])); temp[w][u]=temp[u][w];
			pmax(temp[u][v],f[u][v],d(f[w][w])); temp[v][u]=temp[u][v];
		}
		for (int k=1;k<=n;k++)
		{
			pmax(f[u][k],temp[u][k]); f[k][u]=f[u][k];
			pmax(f[v][k],temp[v][k]); f[k][v]=f[v][k];
			pmax(f[w][k],temp[w][k]); f[k][w]=f[w][k];
			pmax(fmax[k],f[u][k],f[v][k],f[w][k]);
			pmax(fmax[u],f[u][k]);
			pmax(fmax[v],f[v][k]);
			pmax(fmax[w],f[w][k]);
			pmax(fmaxall,fmax[k]);
		}
		pmax(fmaxall,fmax[u],fmax[v],fmax[w]);
	}
	int ans=0;
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<=n;j++)
		{
			if (i==j&&j==a[N-1]) pmax(ans,d(f[i][j]));
			else pmax(ans,f[i][j]);
		}
	}
	printf("%d\n",ans+del);
	return;
}