CF900D Unusual Sequences
题目
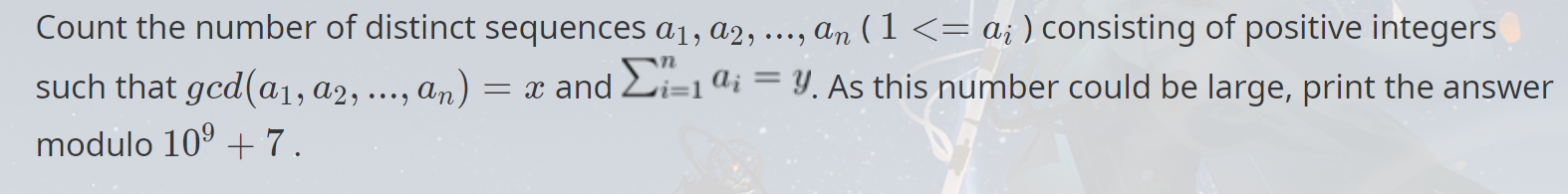
给定一个数列的 \(\gcd\) 和总和,求这样的数列有多少个。(\(x,y\le 10^9\))
分析
略解:
显然可以先转化为求 \(\gcd=1\) ,和为 \(n\) 的数列个数。
首先不考虑 \(\gcd=1\) 的条件,发现其实等价于求正整数解个数,于是有插板法得到的结论:\(\dbinom {n-1}{k-1}\)
然后这里要考虑所有的序列长度,也就是 \(\large \sum\limits_{i=1}^{n}\dbinom {n-1}{i-1}=\sum\limits_{i=0}^{n-1}\dbinom {n-1}{i}=2^{n-1}\)
那么设 \(\large g(x)=2^{x-1}\) ,且 \(\large g(x)=\sum\limits_{d\mid x}f(d)\) ,则我们可以看一下 \(f\) 的意义:\(\gcd\) 为 \(1\) 时,数列之和为 \(d\) 的不同数列个数。
把这个意义带进去不难发现这是正确的。
这个 \(f\) 不正是我们要求的答案吗!而这里又有莫比乌斯反演的形式,于是直接通过 \(g\) 反演出 \(f\) 即可。
化简一下就能得到:
于是直接枚举因数暴力算即可(这里可以光速幂但是没必要,可以优化掉一个 \(\log\))
详解:
应该是先设出 \(f(n)\) 表示 \(\gcd=1\) ,和为 \(n\) 的数列个数,再设 \(h(x,y)\) 表示 \(\gcd =x\) 且 \(sum=y\) 的数列个数,发现 \(h(x,y)=f(\dfrac yx)\)
然后考虑这个 \(f\) 卷上 \(I\) 是什么样子的(就是想尝试通过反演来算):
\[\large \sum\limits_{d\mid x}f(d)=\sum\limits_{d\mid x}f(\dfrac xd)=\sum\limits_{d\mid x}h(d,x) \]这是什么?这不就是:对于一个固定的和,其对应数列所有可能的 \(\gcd\) 对应的所有方案数的和!
这个东西就很好写了,就是对于一个方程给定和求正整数解的个数,我们直接有结论:\(\dbinom {n-1}{k-1}\)
但是因为这里的方程项数不固定,所以我们还要枚举一下:\(\large \sum\limits_{i=1}^{n}\dbinom {n-1}{i-1}\)
这不就是组合数的行求和吗?
也就是 \(\large 2^{n-1}\)
那么 \(f*I\) 是好求的,于是我们直接设函数为 \(g=f*I\) ,不就可以通过莫比乌斯反演来求出 \(f\) 了吗!
那么也就是:
\[\large f(n)=\sum\limits_{d\mid n}\mu(d)g(\dfrac nd)=\sum\limits_{d\mid n}\mu(d)\cdot 2^{\frac nd-1} \]直接枚举因数即可。
代码
注意这里要使用分解质因数的办法暴力求出莫比乌斯函数,而这里进一步使用了 \(Pollard-Rho\) 算法优化。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ull unsigned long long
#define inc(x,y,mod) (((x)+(y))>=(mod)?(x)+(y)-(mod):(x)+(y))
#define dec(x,y,mod) ((x)-(y)<0?(x)-(y)+(mod):(x)-(y))
#define rep(i,x,y) for(int i=(x);i<=(y);i++)
#define dep(i,y,x) for(int i=(y);i>=(x);i--)
const int N=1e6+5,M=2e5+5,MOD=1e9+7;
int n,m;
ll Ans;
bool vis[N];
#define ull unsigned long long
#define ld long double
inline ll mul(ll x,ll y,ll mod){
ll res=x*y-mod*(ll)((ld)x/mod*y);
if(res<0)return res+mod;
if(res<mod)return res;
return res-mod;
}
ll QuickPow(ll x,ll y){
ll res=1;
for(;y;y>>=1,x=x*x%MOD) if(y&1) res=res*x%MOD;
return res;
}
ll Quick_Pow(ll x,ll y,ll mod=-1){
ll res=1;
for(;y;y>>=1,x=mul(x,x,mod)) if(y&1) res=mul(res,x,mod);
return res;
}
ll test[3]={2,61};
inline bool Miller_Rabin(ll x){
if(x==1) return false;
ll t=x-1,k=0;
while(!(t&1)) t>>=1,k++;
for(int i=0;i<2;i++){
if(x==test[i]) return true;
ll a=Quick_Pow(test[i],t,x),Nex=a;
for(int j=1;j<=k;j++){
Nex=mul(a,a,x);
if(Nex==1&&a!=1&&a!=x-1) return false;
a=Nex;
}
if(a!=1) return false;
}
return true;
}
inline bool prime(ll x){
if(x==46856248255981ll||x<2)return false;
if(x==2||x==3||x==7||x==61||x==24251) return true;
return Miller_Rabin(x);
}
ll gcd(ll x,ll y){return y?gcd(y,x%y):x;}
inline ll f(ll x,ll c,ll mod){
ll res=mul(x,x,mod)+c;
return res<mod?res:res-mod;
}
inline ll Pollard_Rho(ll x){
ll c=rand()%(x-1),s=0;
for(ll lim=1;;lim<<=1){
ll t=s,now=1;
for(ll j=1;j<=lim;j++){
s=f(s,c,x);
now=mul(now,abs(s-t),x);
if(!now){ll d=gcd(s,x);if(d>1)return d;return x;}
if(j%127==0){ll d=gcd(now,x);if(d>1)return d;}
}
ll d=gcd(s,x);
if(d>1) return d;
}
}
ll Maxn;
ll t[N],q,id,fl;
map<int,int>Map;
inline void GetFact(ll x){
if(fl) return ;
if(x<=1) return ;
if(prime(x)){
if(Map[x]) fl=true;
Map[x]=1;id++;
return ;
}
ll p=Pollard_Rho(x);
while(p>=x) p=Pollard_Rho(x);
GetFact(x/p),GetFact(p);
return ;
}
inline int mu(int x){
fl=false;id=0;map<int,int>mapp;swap(mapp,Map);
GetFact(x);
if(fl) return 0;
return ((id&1)?-1:1);
}
inline void incc(ll &x,ll y){x+=y;if(x>=MOD)x-=MOD;}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>m;
if(m%n){puts("0");return 0;}
m/=n;
for(int i=1;i*i<=m;i++) if(m%i==0) incc(Ans,1ll*mu(i)*QuickPow(2,m/i-1)%MOD),incc(Ans,(m!=i*i)*1ll*mu(m/i)*QuickPow(2,i-1)%MOD);
cout<<(Ans%MOD+MOD)%MOD;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号