P1020 导弹拦截 || 偏序集与 Dilworth 定理

时隔 $2$ 年，终于把导弹拦截的 $O(n \log n)$ 写了。

偏序关系

现在有一个二元关系 $R$，不妨设 $R$ 是定义在 $S$ 上的，如果 $R$ 满足一下性质，称其为偏序关系。

（下面的小于等于号并非真的是小于等于号，而是偏序关系的符号，但 $\le$ 也是一个偏序关系）

自反性： $a \le a, a \in S$
传递性：$\forall a,b,c \in S \ \ ,a \le b,b\le c \to a \le c$
反对称性：$\forall a,b \in S, a \le b,b \le a \to a=b $

偏序集

偏序集就是由定义在 $S$ 上的偏序 $R$ 和集合 $S$ 组成的，记作 $(S,R)$，最经典的例子就是 $(Z, \le )$，此处的小于等于是真的小于等于号。

对于 $S$ 中的元素 $a,b$ 如果 $a \le b$ 或 $b \le a$，则称 $a,b$ 可比，此处小于等于号是偏序关系的符号。

哈斯图

对于元素 $x$，若有 $x < y$ 且不存在 $z$，使得 $x < z < y$，就连出来一条 $x \to y$ 的有向边，这样生成的图就是哈斯图。

比如集合 $\{1,2,3,4,6,8,12 \}$ 上定义关系 $\{ (a,b) | a \ 整除 \ b \}$ 画出哈斯图就长这样：

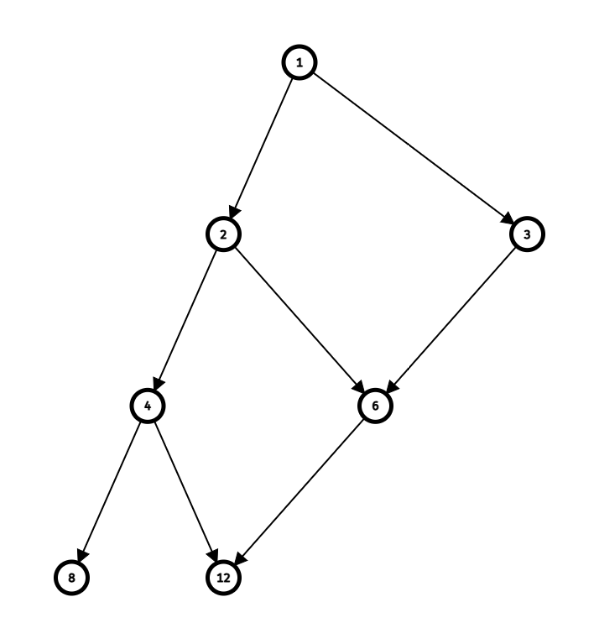
显然哈斯图一定是 DAG。

偏序集上的链与反链

链：链上任意两两元素都可比。

反链：链上任意两两元素都不可比。

Dilworth 定理

对于任意有限偏序集，都有最小链划分（不可交）所划分的链的个数等于最大反链所包含元素，对上图显然成立。

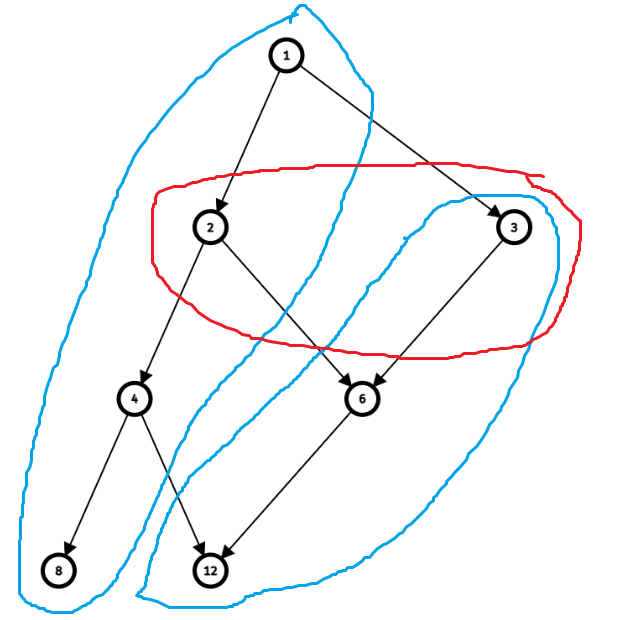
蓝色是最小链划分，红色是最大反链。

证明

利用数学归纳法，先假设有一偏序集 $(S,\le )$，$|S|=n$。

当 $n=1$ 时，结论显然成立。

假设 $n=k$ 的结论已被证明，下面证明 $n=k+1$ 时也成立。

设 $A$ 是最大反链，计为 $A=\{a_1,a_2,\dots ,a_w \}$。

定义:
$D(A)= \{x | \exists a \in A,x < a \}$
$U(A)= \{x | \exists a \in A,x > a \}$

有 $S=A \cup D(A) \cup U(A) $。

如果存在最大反链 $A$，使得 $D(A),U(A)$ 均非空。因为 $A$ 是 $S$ 的最大反链，所以 $A$ 也是 $A \cup D(A)$ 的最大反链由归纳假设 $A \cup D(A)$ 可以划分为 $c_1,c_2,\dots ,c_w$ 共 $w$ 条链，$c_i$ 的最大元为 $a_i$，同理 $A \cup U(A)$ 可以划分 $d_1,d_2,\dots ,d_w$ 共 $w$ 条链，$d_i$ 的最小元为 $a_i$，于是 $S$ 就可以划分为 $c_i \cup d_i $ 共 $w$ 条链。
反之，那么每条反链 $A$ 都有全部的最大元或全部的最小元。在 $S$ 中选择极大元 $y$，再选择极小元 $x$ 满足 $x \le y$。 $(x,y)$ 一定构成一条链，因为 $x,y$ 一定是最小元或最大元之一，所以 $S-(x,y)$ 一定会使反链大小减 $1$，利用归纳结论，由此时的划分数量有 $w-1$ 个，此时再加上 $(x,y)$ 恰好有 $w$，结论成立。

~~画个图感觉有助于理解~~

我们考虑上图那个例子，$A=\{2,3\},D(A)=\{1 \},U(A)=\{4,6,8,12 \}$，注意到 $A \cup D(A)$ 可以划分为两条链，$A \cup U(A)$ 可以划分为两条链且互相对应的两条链可以合并。

我们再考虑一个例子，上图假设只有 $S=\{1,2,3 \}$ 三个点，$U(A)$ 为空，考虑选取最大元 $y=3$，最小元 $x=1$ 注意到其构成一条链，删去这条链后，$A$ 就删去了一个 $3$，考虑 $A$ 必然只会减少一个元素，这样利用归纳结论就证明完了。

~~主播主播还有没有更说人话的证明~~

我们考虑这样一个过程 $A$ 中每个元素都向上向下走，尽可能多走，考虑一定能走完全图，否则就不是最大的反链，最后在 $A$ 处合并，这样得到的一定是一种链的划分。