【题解】F. Wildflower

题意

给定一棵有根树，你可以在树的节点上写 \(1\) 或 \(2\)。使得任意子树，在子树内节点之和，两两不同，求方案数。

分析

显然这棵树最多有两个子节点，否则一定没有方案，因为一共就两种颜色，要给大于两个点染色，无法做到颜色不同。

如果只有一个叶节点，可以任填，答案就是 \(2^n\)。

如果有两个叶节点，我们画个图：

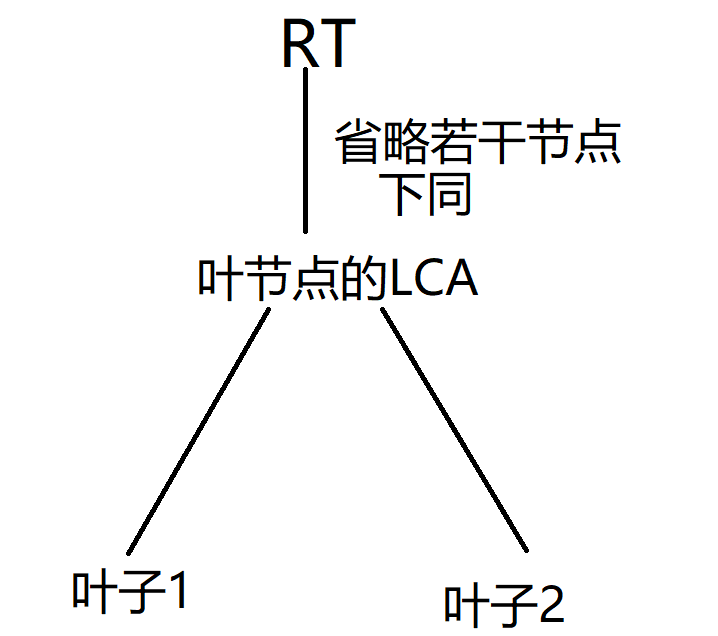
假设叶节点为 \(x,y\)，其到 LCA 的距离为 \(dis_x,dis_y\)，\(dep_{lca}\) 表示 LCA 节点的深度。

不妨设 \(dis_x \ge dis_y\)。

当我们给 \(x\) 染上 \(1\)，\(y\) 染上 \(2\) 时：

我们注意到 \(x,y\) 往上至少染 \(dis_y\) 个 \(2\)。

证明：我们当第一个不符的是在 \(x\) 处，则显然对应到 \(y\) 上，对应节点的儿子的子树和一定等于原节点子树和，当第二个不符的在 \(y\) 处，对应的 \(x\) 处子树和同样等于原节点子树和，大家可以画个图来理解。

当我们给 \(x\) 染上 \(2\)，\(y\) 染上 \(1\) 时：

我们只需要一起染色至 LCA（LCA 不染色），同样是染色为颜色 \(2\)。

那么这样做有一个缺陷，当 \(dis_x=dis_y\) 时，\(x\) 往上染色就会染色到 LCA 上，这样是不需要的，所以这一类答案就是 \(2 \cdot 2^{dep_{lca}}\)，式子开头是因为 \(x,y\) 可以互换。

当 \(dis_x>dis_y\) 时，我们总结一下式子：

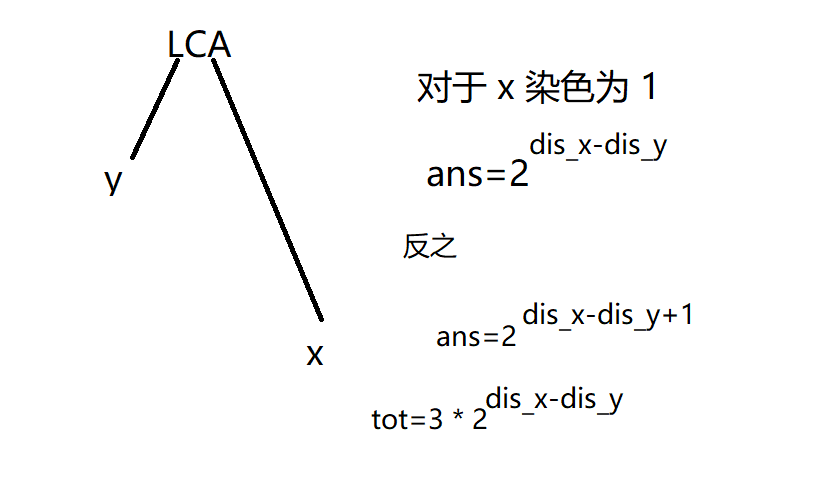
两者式子不同是因为两者有一个需要往上多染色一层。

之后在 LCA 以上的节点任意染色，乘起来就做完了。

代码

submission-323720152